考虑速度与能量消耗的电动车辆路径规划

邢思远（中国矿业大学 矿业工程学院，江苏 徐州 221116）

0 引言

国际社会普遍认为，引起气候变化的重要因素是由于温室气体的过度排放。物流运输业作为消耗石油能源的重要行业，也成为温室气体的显著排放源[1]。随着“碳排放，碳中和”、绿色物流、新能源汽车政策的提出，以及纯电动新能源汽车相比燃油车所具有无直接碳排放的优势，可以预见电动汽车将会成为物流运输的重要交通工具[2]。现阶段电动汽车自身仍然存在较为明显的劣势：续航能力较差，远距离行驶能力较弱以及行驶过程中充电不方便等[3]。本研究根据电动汽车自身特性，研究以传统车辆路径问题（Vehicle Routing Problems，VRP）为基础的带时间窗的电动车路径规划（Electric Vehicle Routing Problem with Time Windows，EVRPTW）。文中对电动车辆能耗量以及行驶速度作为新的影响因素，进行了配送过程中能耗计算及速度对能耗影响的研究。

EVRPTW 是VRP 的变体问题，二者同属于NP-hard 问题，求解方法主要以遗传算法（Genetic Algorithm，GA）、禁忌搜索算法（Tabu Search，TS）、模拟退火算法（Simulated Annealing，SA）等智能优化算法为主。Schneider 等人[4]使用混合禁忌搜索和可变邻域搜索解决考虑充电站的EVRPTW，提出了一个数学模型，同时验证了算法的有效性。葛显龙和竹自强[5]设计并改进的禁忌搜索算法来解决基于换电策略的EVRPTW。贾永基等人[6]使用模拟退火算法结合变邻域的混合启发式算法来解决考虑时变速度和动态需求的EVRPTW。以上研究表明智能优化算法能够有效的解决EVRPTW 问题，因此本研究也使用智能优化算法来解决EVRPTW 问题。

因为电动车辆具有明显的“里程焦虑”，因此研究中考虑电量消耗变得十分必要。当前在EVRPTW 中考虑电量消耗的研究较少，大多EVRPTW 的研究重点考虑充电策略对路径规划的影响。针对电动车续航问题，李进[7]提出一种基于换电模式的EVRP，建立了考虑电动车使用成本以及能量消耗成本的规划模型，同时使用改进的遗传算法来求解对应模型。针对电动汽车路径规划问题，学者李嘉等人[8]将载重和车辆旅行距离作为电动汽车能耗影响因素来进行研究，通过基于模拟退火和变邻域搜索的混合启发式算法来求解问题。Desaulniers 等人[9]研究了不同充电策略对电动送货卡车在有软时间窗限制的情况下向客户配送货物的总成本影响。杨珺等[10]在忽略载重速度对能量消耗影响的条件下，同时考虑物流配送系统中充电站选址与路径优化问题，建立相应模型，通过禁忌搜索与改进Clarke-Wright 节约的多阶段算法来求解问题模型。对于电动汽车能耗问题，甘俊伟等人[11]在对生鲜背景下EVRPTW 的研究中建立能耗估算模型，通过使用贪心算法来求得模型的最优解。Zou 等人[12]在考虑速度与载重的因素下，建立了以行驶速度为决策变量的数学模型，通过启发式算法对问题进行求解。

通过Fetene 等人[13]的研究可知，电动车量的电量消耗与车辆的载重、速度、行驶距离有关。对行驶速度进行优化能够减少车辆电量的消耗，传统的EVRPTW 的研究通常假设车辆速度是固定的常量，不考虑速度变化对能量消耗的影响，同时车辆的行驶速度在实际运输过程中是允许被调节的。因此本研究在EVRPTW 背景下对行驶速度以及能量消耗进行了综合考虑。

1 模型构建

1.1 问题描述

本研究以完全图G (N,A)来表示行驶网络，N={0,1,2,…,n}为位置点集合，C={1,2,…,n}为需求客户集合，A={(i,j);i,j∈A}为两位置点之间弧的集合，0 为仓库，即配送中心，D=(dij)为任意两点之间的距离集合，研究车辆为同质车辆，K={1,2,…,m}代表车辆集合，m 为车辆允许的最大使用数，车辆装载量为Q。初始电量为B，bij表示弧(i,j)消耗电量vij表示在弧(i,j)上的行驶速度,]表示弧(i,j)行驶速度的范围，为行驶速度的下限，为行驶速度的上线，行驶速度范围通过时间窗约束与道路允许速度范围进行确认。[ei,li]表示行驶网络中各个地点的允许服务的时间窗口，ei为地点i 最早允许服务时间，li为地点i最迟允许服务时间。时间窗口为硬窗口，即不允许晚点开始服务，但可以在提前到达的情况下等待。ai表示车辆到达顾客点i的时刻，si为车辆在顾客点i 的服务时间。qi表示顾客点i 的需求量。决策变量为vij和Xijk。

不同于传统的EVRP，本研究在满足约束条件的情况下将对两点间弧的行驶速度进行优化，以达到总成本最优。本研究的目标就是寻找最优的车辆、路线和路线上的速度，使得在满足约束的条件下达到总成本最小化。为了便于模型建立，研究假设路况与道路状态良好。

本研究设定的约束条件如下：车辆从仓库出发服务需求客户配送，服务完所有需求客户后返回配送中心；每个需求顾客点都需被访问并且仅允许访问一次；每条配送路线的顾客总需求不允许超过车载量Q；每条配送路线的顾客总电量消耗不大于B。车辆在每个弧段的行驶速度必须满足行驶速度范围约束。

1.2 电动汽车能量消耗模型

多数关于EVRP 的研究将汽车的能量消耗建模为行驶距离或者速度的线性函数。将速度与能耗关系简化为线性关系，在一定程度上影响车辆能耗的准确性。本文采用Goeke 和Schneider[14]研究中开发的模型来计算电池能量的消耗，该能耗估算方法分为三个步骤。首先根据Bektas 和Laporte[15]所提出的模型确定车辆机械功率PM，机械效率需要克服滚动阻力和空气动力阻力，并且受到重力影响。其中：W 表示车辆自重，U 表示车辆载重，a 表示加速度，本研究不考虑加速与制动过程，因此a=0。cd表示空气阻力常数，ρ 表示空气密度，A 表示车辆前方最大表面积，g 为重力常数，z 表示坡度角，cr为行驶摩擦系数。

根据Goeke 和Schneider 研究中发现的关系，将PM被转换成电机需要提供所需机械功率的电能PE。如公式（2）所示，其中φ 是通过将y 轴为零的齐次线形回归线拟合到一组观测值得到的回归系数。

在不考虑环境温度以及电池当前充电水平的情况下，使用电池电能PE与电池能PE的转换关系如公式（3）所示。其中φ 代表电池效率的回归系数。

通过以上三个步骤以及每条两点间的行驶时间tij确定的情况下，可以得出电动汽车每两点间的电池能耗bij的计算公式（4），其中Pij为弧(i,j)的机械效率PM：

由式（5）可以确定电池能耗与速度、载重和行驶距离有重要关系，其中电量消耗与速度呈非线性关系。同时在具有时间窗约束以及载重距离确定的条件下，存在一个最优速度使得电量消耗达到最小。

电能消耗公式有关参数设置：引力常数g 为9.81m/s2，摩擦系数cr为0.1，阻力系数cd为0.7，密度ρ 为1.204 1kg/m3，电动车电量能耗效率回归系数φ 为1.184 692，放电模式下电池效率的回归系数φ 为1.112 434。

1.3 建立成本优化模型

基于以上描述，建立的成本优化模型如公式（6）至公式（16）。

目标函数式（6）表示求解最小总成本，包括启动车辆成本、能量消耗成本、里程成本（司机成本、其他路费）以及不满足时间窗约束、载重约束、电量约束的惩罚成本；式（7）与式（8）表示每个客户点必须被访问且仅被访问一次的约束；式（9）为配送中心约束，即所有车辆均从配送中心出发，服务结束后返回配送中心；式（10）表示每辆车的容量约束；式（11）表示每辆车的电量约束；式（12）与式（13）为需求客户的时间窗约束，M 为足够大的整数；式（14）与式（15）为到达时间、等待服务时间的约束条件；式（16）表示决策变量的约束条件。符号定义如表1 所示。

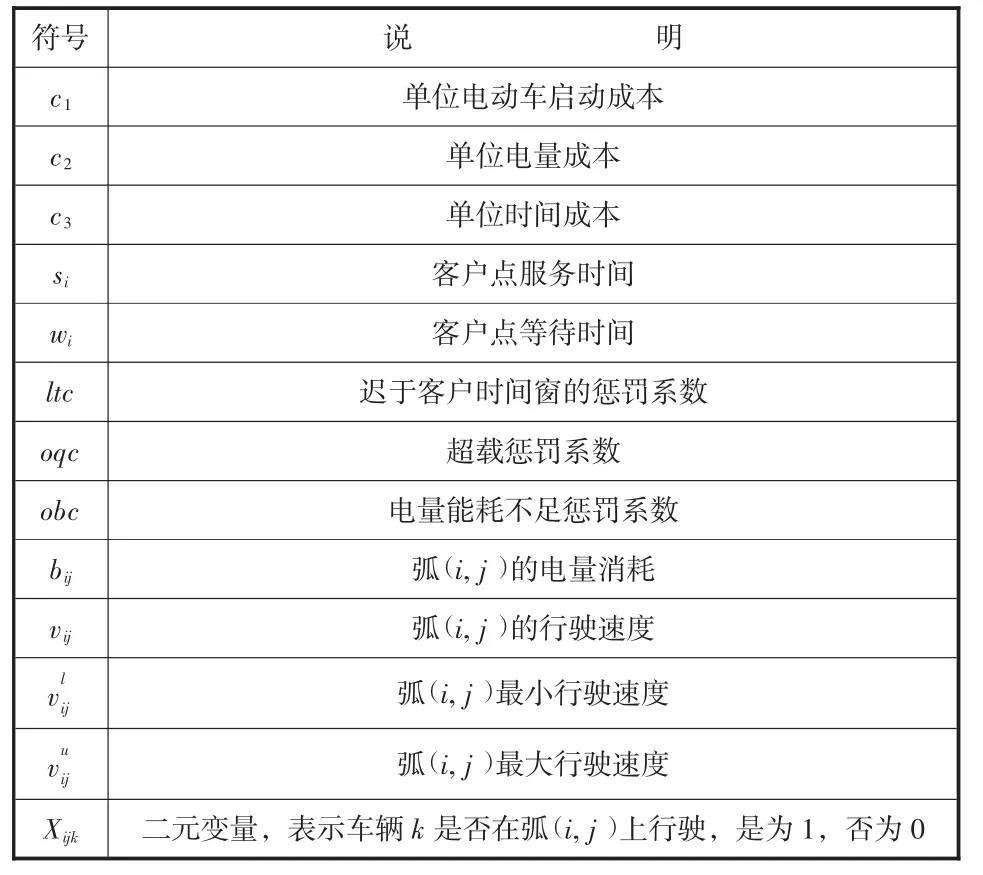
表1 符号含义

2 两阶段启发式算法

EVRPTW 是一种显著的NP 难问题，本研究中将速度作为决策变量，采用一种两阶段算法进行路径与速度优化。算法基本思想：第一阶段，通过使用模拟退火算法来优化不同固定速度v*下的路径，通过目标函数来判断不同固定速度v*下的最优路径，选择其中最优固定速度v*和路径信息作为第一阶段的解。

第二阶段，通过第一阶段所得速度以及路径信息，确定各弧段允许的速度范围，具体方式为：通过客户时间窗确定时间窗约束下的速度范围，其中最小速度不能小于道路允许速度，为了避免局部优化破坏全局优化，因此弧段最大速度为第一阶段全局最优速度。接着利用遗传算法对路径中各弧速段度进行优化改进，同时计算总成本。

具体步骤如下：

（9）读取路径信息，确定客户点配送顺序，根据确定客户时间窗与道路允许速度确定弧段速度上下限，生成初始种群。

（10）计算初始种群中各个个体适应度，将初始种群中最优个体设置为bestV，接着进行选择、交叉、变异操作产生新的子种群newV。

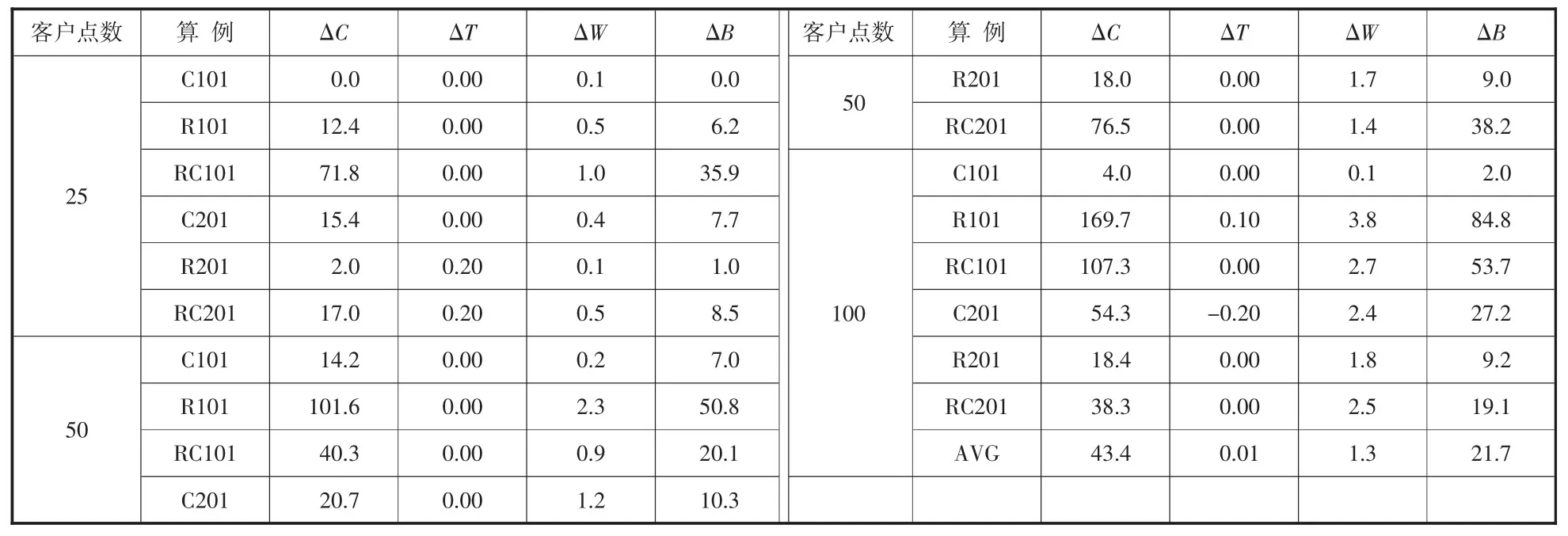
（11）计算所得新种群的适应度，若满足f (newV)

（12）判断迭代次数是否达到终止循环的次数。若达到则输出最优速度，否则继续（9）—（11）步骤。

（13）更新全局能耗量、总时间、总成本并输出结果，算法结束。

3 数值实验

3.1 实验算例构造

本研究算法使用MatlabR2020b 实现，运行在Intel i5-6200U、内存8G 的笔记本电脑上。利用Solomon's 标准算例（R1、R2、C1、C2、RC1 和RC2）进行数值实验。该算例根据客户地理分布规律，被分为随机分布（R1、R2）、集群分布（C1、C2）和二者混合分布（RC1、RC2），分别选取客户数为25，50，100 的算例，对每组测试实例进行10 次计算，取运算所得的最优解作为该组测试实例的实验结果。

算法参数设置如下：道路允许速度范围设为[40,80]km/h，速度搜索步长6，SA 算法T0为1 000，λ 为0.9，最低温度为0.000 1，当前温度下的链长L0=100。电动汽车电池容量B=50kWh，车辆自重为500kg。GA 算法种群大小，最大遗传代数和个体长度分别为40,20 和20，选择概率，交叉概率和变异概率分别为0.95,0.7 和0.01。

与费用有关的参数设置：车辆启动成本c1为200 元/辆，能耗成本c2为2 元/千瓦时，行驶里程成本c3为1.5 元/千米。车辆早于允许服务时间的惩罚系数为0，车辆晚于允许服务时间的惩罚系数为1 000。车辆负荷过载惩罚系数为10 000，电量约束系数为10 000。

3.2 运行结果分析

使用本研究提出的两阶段启发式算法得到的计算结果如表2 所示，固定速度V*为第一阶段优化所得。表2 中C、T、W、B分别代表配送过程所需总成本、总时间、等待时间以及配送过程中的能耗量。通过表2 可以得出，随着算例的类型以及规模发生变化，算法第一阶段得到的全局最优速度也会发生变化，速度变化范围为54～66km/h。对比不同类型的算例可以得出，在同等客户点数条件下，随机分布（R1、R2）算例相较于集群分布（C1、C2）算例所需成本更高，二者混合分布（RC1、RC2）算例所需成本处于随机分布与集群分布之间。同时可以看出在同等客户数条件下，不同分布类型所需配送时间，等待时间以及能量消耗是不同的，相较于其他两种分布类型，集群分布（C1、C2）算例在相同客户数条件下所需配送时间，等待时间更多，能量消耗更少。

表2 两阶段启发式算法计算结果

表3 为第一阶段固定速度与第二阶段弧段优化速度对比结果，其中ΔC 表示两阶段成本差，ΔT 表示两阶段时间差，ΔW 代表两阶段等待时间差，ΔB 代表两阶段能耗量之差。

表3 两个阶段计算结果对比

对比第一阶段与第二阶段所得结果，弧段速度优化下所得到的时间结果相对于第一阶段固定速度下得到的行驶时间只有轻微变化，行驶时间变化在-0.2～0.2 之间。但不同优化策略下的等待时间却有明显变化，第二阶段所得结果相较于第一阶段等待时间平均减少2.93%。电量消耗结果也有明显变化，第二阶段所得结果相较于第一阶段电量消耗平均减少12.6%。配送过程所需总成本也有变化，第二阶段所得结果相较于第一阶段配送总成本平均减少1.5%。

上述内容说明算法第二阶段对弧段速度进行优化能够改进一阶段解得质量。同时表3 结果表明，针对相同类型的不同客户数的算例，客户数量越多，两阶段启发式算法所减少的电量消耗，等待时间以及总成本越显著。

4 结论

本研究在EVRPTW 模型的基础上，采用考虑速度与载重的电量消耗计算方法，将速度作为目标函数的决策变量，建立了考虑速度、载重与能耗的带时间窗的EVRP 模型。通过使用两阶段启发式算法来求解所建模型，首先使用SA 算法进行全局速度与路径优化，得到满足约束条件的最优路径以及全局最优速度；其次使用GA 算法对弧段速度进行优化，从而得到考虑能耗与速度的最优总成本。

为了证明模型以及算法的有效性，通过Solomon 标准算例构建不同类型的EVRPTW 测试算例。实验结果表明在载重距离固定的条件下，不同类型、不同数量的算例的全局最优速度会存在差异；在本研究的模型下，考虑弧段速度优化的路径规划比全局固定速度下的路径规划能够更加有效地减少电量消耗，降低总成本。综上所述，考虑速度优化的路径规划能够更合理的使用能量，减少车辆使用数目，降低总成本。