面向纱管抓取的仿生末端执行器手指设计与分析

王静国,管声启

(西安工程大学 机电工程学院,陕西 西安 710048)

在棉纺织行业中,络筒(又称络纱)是织前准备的第一道工序,其任务是将来自纺部的管纱或绞纱在络筒机上加工成符合一定要求的筒子。络筒作为纺纱的最后一道工序和织造的首道工序,起着承上启下的“桥梁”作用,在纺织领域中占有重要的地位。纱管作为织造的第一原料,纱管的上料效率决定了后续织造工序的整体效率。目前,细纱机出来的纱管在进入络筒机时需要人工进行抓取纱管和插纱管,该过程不仅耗费大量的人力资源,且生产效率较低。传统的络筒插纱机在抓取纱管时,采用两指平行抓取方式,没有形成稳定的力闭合抓取形态,导致纱管抓取掉落,影响工作效率,同时部分络筒插纱机仅考虑对纱管中间部位进行抓取,容易对纱线造成损伤,不利于纺织高质量纱线。洪秀琴等[1]利用平行四边形原理,模拟人手旋搓的动作对纱管顶部进行夹持。朱保利等[2]通过滚珠丝杠副的相互运动实现夹片之间夹紧动作,但其抓取范围较小,对纱管尺寸的适应性不佳。因此,设计性能优良的末端执行器,实现对不同尺寸纱管的稳定抓取是提高纺纱效率关键。

近年来结合了纺织学科及机器人学的纱管自动化抓取技术逐渐成为国内外研究热点,随着仿生学的不断深入研究,以欠驱动方式为特征的仿生末端执行器因其具有灵巧性等诸多优点,被广泛应用到工业现场。欠驱动机械手的传动类型主要分为肌腱式[3-6]、连杆式[7-8]、齿轮式[9-10]等,连杆式与齿轮式的机械手因其抓取力较大,较多用于抓取钢铁棒料等工业现场,但受其机械结构限制,拟人化抓取特征难以实现;而肌腱式机械手抓取范围较广,腱绳在一定程度模拟人手肌肉的功能,因而比较容易实现拟人化自适应抓取特征,可以较好的应用在纺织轻工业领域。文献[3-6]中仅利用弹簧或扭簧使手指复原到初始位置,没有考虑弹簧刚度对抓取姿态的影响。实际上,关节弹簧的配置对关节运动顺序及手指抓取力发挥着重要作用[11]。

欠驱动末端执行器的抓取性能很大程度上取决于结构设计而不是控制方法[12]。目前末端执行器对物体抓取策略(指尖抓取和包络抓取)的选择需要人为调控,未能实现抓取策略上的被动选择。Ciocarlie M等[13]优化了屈肌腱和伸肌腱的肌腱路径,根据抓取对象的大小被动地实现平行或包络抓握。在实际应用中,为避免包络抓取影响纱管表面纱线的质量,往往采用指尖抓取纱管顶部的模式。因此指尖结构的优化设计是实现稳定抓取纱管的前提。Chen等[14]依据指尖抓取力利用逻辑回归模型预测抓取稳定性的概率。Haas等[15]在被动顺应抓取背景下求解平衡接触力,并以此量化抓取稳定性。Funahashi等[16]考虑手指与物体在接触点的曲率及摩擦接触的情况,利用抓取系统的势能建立刚度矩阵分析指尖抓取稳定性。Yamada等[17]利用指尖抓取刚度矩阵的差分矩阵的正定性,分析证明滚动接触抓取比滑动接触抓取更稳定。目前针对指尖抓取的稳定性研究较多应用在在二指平面抓取,其适用范围有限。

本文合理设置弹簧使得手指具备结构上的被动顺应性,实现指尖抓取与包络抓取的自适应切换,将指尖抓取扩展到三指空间抓取领域。针对指尖抓取纱管顶端的模式,设计一款新型的欠驱动仿生末端执行器,基于人手抓取机制规划手指内部肌腱传输路径,并以手指合理的运动特征为依据,优选各关节的弹簧刚度,实现手指结构的被动柔顺性,随后从系统势能的角度量化三维空间抓取的稳定性指标,进而设计手指指尖最佳形状,最后进行抓取实验,验证设计和分析的合理性。

1 仿生末端执行器的结构设计

络筒工序是根据工艺要求,将原纱加工成符合后道工序生产或销售的卷装(筒子),管纱是原纱的卷装主要形式之一,广泛用于棉、毛、麻及各种化纤短纤纱。

细纱机上纺制的管纱,绕纱长度仅为2～3 km(中等线密度纱),如果直接用来整经或经无梭织机供纬,会因频繁更换纱管严重影响后道工序的生产效率。因此,应在络筒工序将管纱加工成容量较大、适合后道工序高速退绕的筒子。目前常见的纱管型号如表1所示,所抓取的纱管端部外直径的尺寸范围为18～37 mm。纱管参数见图1。

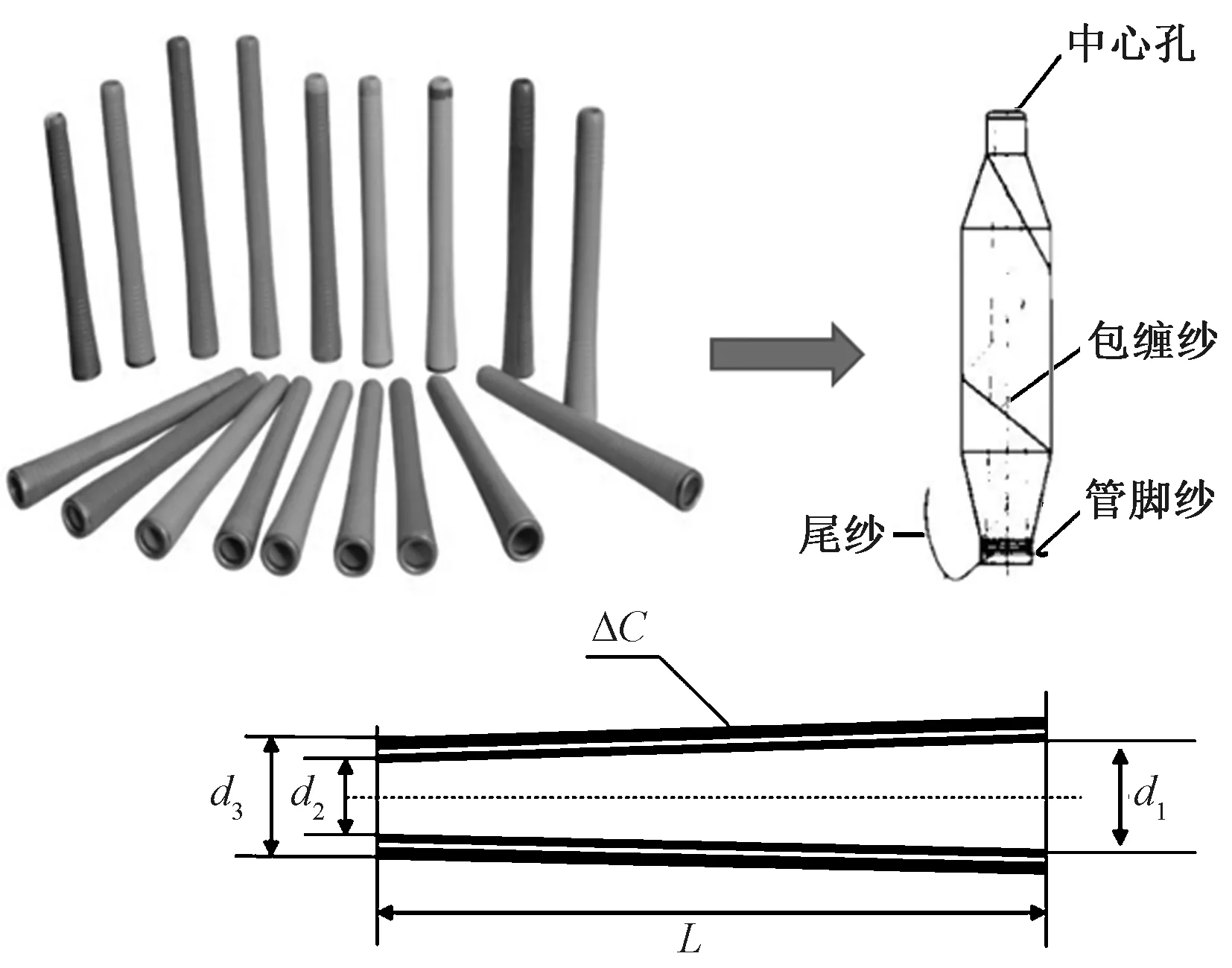
图1 纱管参数图Fig.1 Bobbin parameter diagram

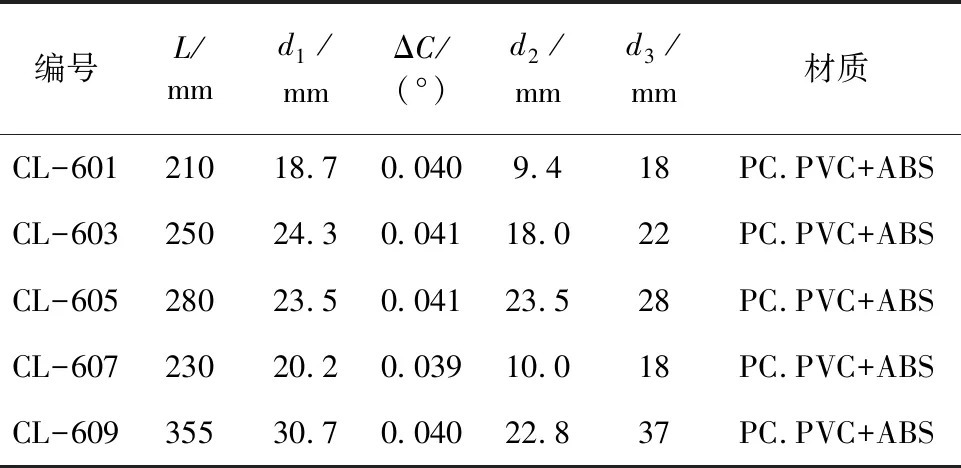
表1 纱管尺寸表Tab.1 Bobbin size table

研究人手的动作原理,发现肌腱能够能传导肌腹收缩产生力,牵拉指骨使之产生运动。人手结构图如图2所示,从生物力学观点来看,腱鞘为肌腱滑动提供力学支点,进而改变力的方向,有利于发挥肌腱的滑动功效。仿照此传动原理,设计的末端执行器手指如图3所示,整根手指由近指节、中指节、远指节、大小滑轮、弹簧、钢丝绳肌腱和手掌链接组成。虚线段是步进电动机连接的主动肌腱,其中转折处的点表示小滑轮心轴,各关节处的黑色圆圈表示大滑轮,L1、L2、L3分别是近指节、中指节、远指节的长度,K1、K2、K3分别是近指关节、中指关节、远指关节处线性弹簧的刚度系数。F3表示指尖接触力,其有许多潜在方向(虚线箭头)。1个单独驱动的肌腱使各个关节弯曲,滑轮实现力的传导并改变力的传递方向,从而实现手指的弯曲,而手指的伸展力由各个关节处的弹簧来提供。

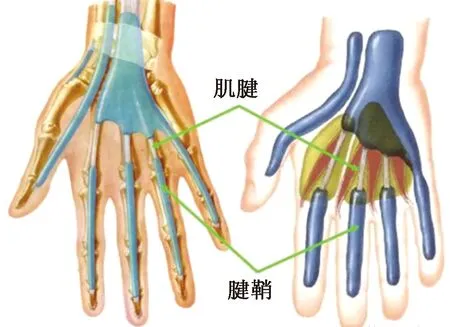
图2 人手结构图Fig.2 Hand structure diagram

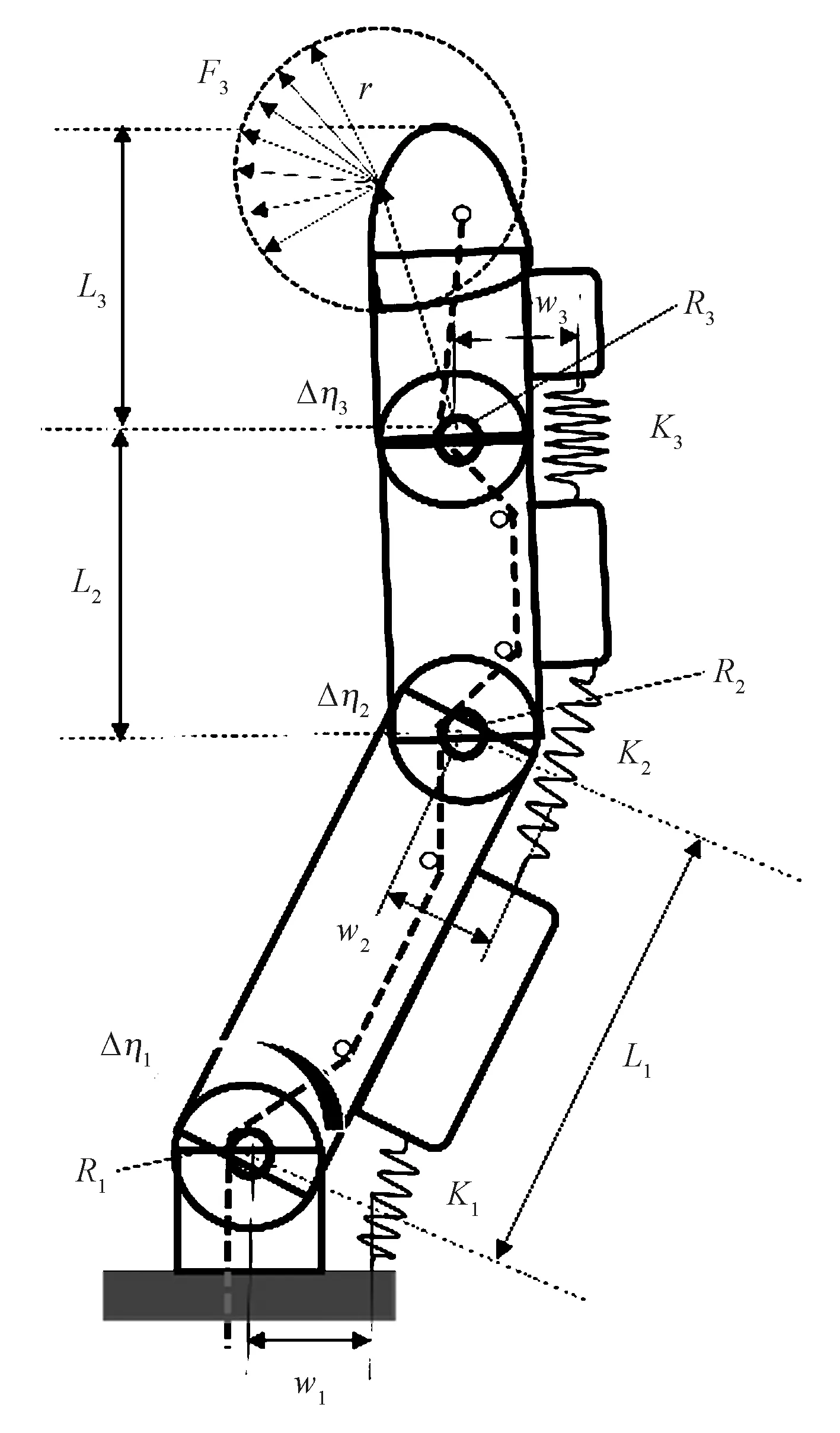
图3 仿生末端执行器手指示意图Fig.3 Finger diagram of bionic end effector

考虑到抓取对象主要是细纱管,其尺寸在18～37 mm范围之内,根据人手的各指节之间的比例关系,确定各指节的长度如表2所示。

表2 手指各指节的参数Tab.2 Parameters of finger segments

现实工厂中,为了提高工作效率,避免频繁的更换末端执行器,则需要机械手具备一定的稳定性和自适应性。在机械手进行抓取任务时,手指的数目越多,抓取越稳定,但同时会增加控制系统的复杂性和驱动系统的压力,因此,有必要在保证抓取任务的前提下,选择合适的手指数量[6]。日常生活中,拇指、食指、中指的使用率最高,抓取特性好,而无名指和小指起辅助作用,因此采用3根手指。该末端执行器整体高为210 mm,宽为165 mm,长为165 mm,共由3根手指和手掌组成,如图4所示,其3根手指采取模块化思想设计,简化其复杂度[18]。针对抓取的作业任务,手指分布需要合理设置,采用三角形式对心分布模式,提高抓取稳定性。

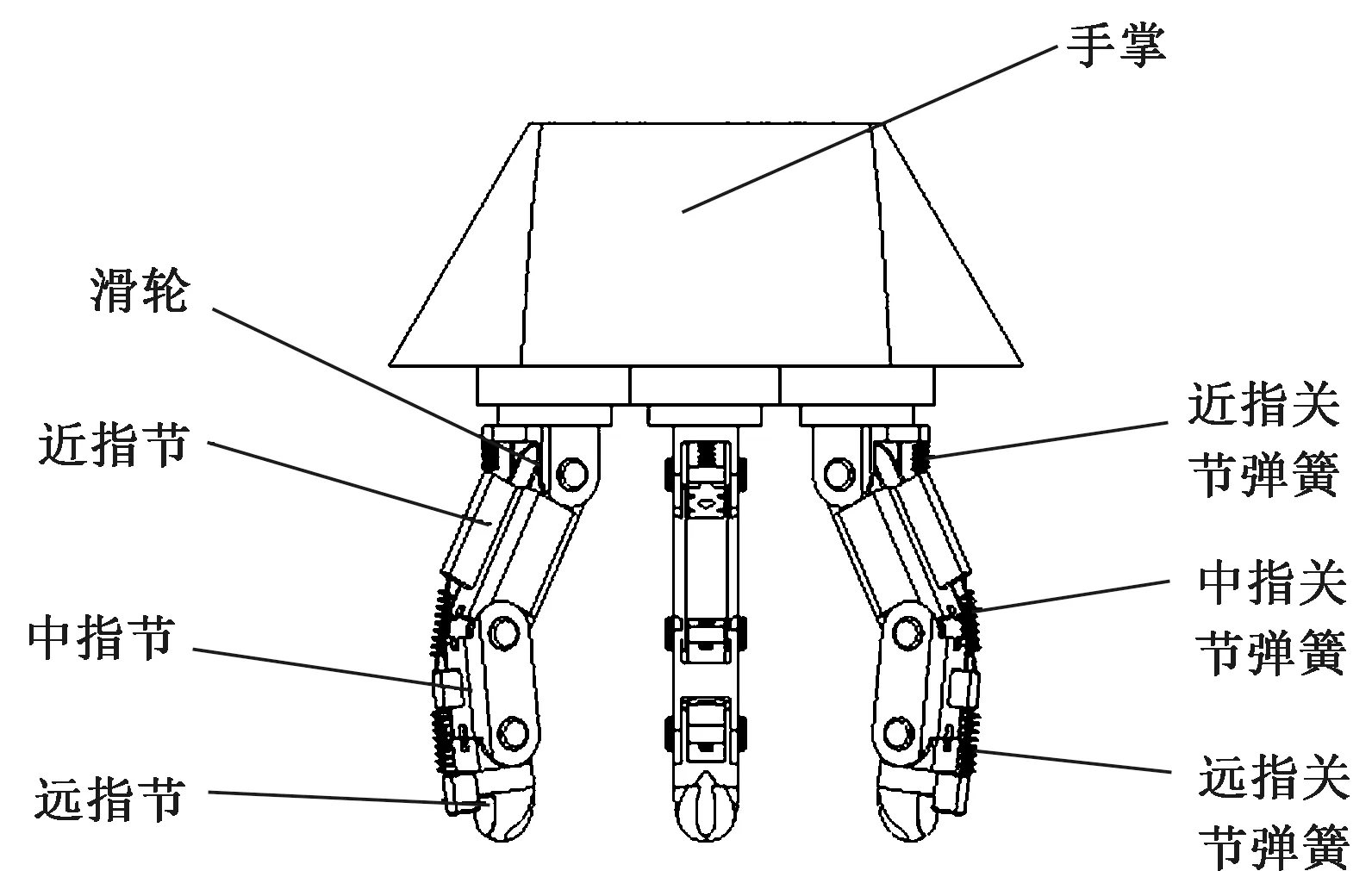
图4 末端执行器装配体Fig.4 End effector assembly

2 手指抓取力的分析与计算

手指接触力对指尖抓握的稳定性有重要影响,因此必须建立驱动力与接触力之间的力传递模型。根据虚功原理得:

(1)

映射雅可比矩阵Jk的元素由关节处的滑轮半径和弹簧力的力矩臂决定,τ是关节向量矩阵,将手指的闭合方向定义为旋转关节的正方向,对映射雅可比矩阵Jk的描述如下:

(2)

其中肌腱张力与弹簧拉力表示为:

(3)

式中:Fti表示弹簧i的拉力,N;Ri表示i关节处的滑轮半径,mm;wi表示i弹簧力的力矩臂,mm;Ki为关节i处的弹簧的刚度,N/mm;Fa表示肌腱的张力,N;Δηi是η1、η2和η3的变化角度,(°);i=1,2,3。由式(1)～(3)得到式(4):

(4)

同理,接触力与关节力矩之间的传输模型如式(5)所示:

(5)

式中:Ji为具有手指的接触力空间到关节力矩空间的映射雅可比矩阵;Fi为关于固定参照系手掌的接触点i的力。

M3是扭矩τ3的力矩臂,所施加的扭矩τ3的大小表示为:

|τ3|=|F3M3|

(6)

所以指尖接触力为:

(7)

从式(7)可以看出,接触力受关节弹簧的影响,随着弹簧刚度的增大,指尖的接触力逐渐减小。

3 手指关节弹簧的优选

考虑到末端执行器中的弹簧处于变载荷、常温下工作,其最大载荷为fmax=8 N,一般工作载荷为f=5 N,工作行程在h=6 mm,考虑旋转关节与弹簧的物理干涉,弹簧外径(D2)不大于10 mm。选用65 Mn弹簧钢丝直径(d)为0.8 mm,则中径D=D2-d=9.2 mm,则根据《机械设计》手册[19],选择D=9 mm,则旋绕比C=D/d=11.25,曲度系数:

(8)

根据预选择的弹簧丝直径0.8 mm,查《机械设计》手册[19]可知[τp]=285 MPa,

(9)

与估值接近,选d=0.8 mm,则D2=D+d=9.8 mm,满足要求。弹簧刚度为:

(10)

取G=79 000 MPa,则弹簧圈数为:

(11)

则取有效圈数为n=11。

弹簧刚度校核,即:

(12)

与所需刚度基本符合。

为实现人手各指节之间的耦合特性,弹簧刚度的选取将直接影响指节的运动特性。仿生末端执行器具备3根手指,呈正三角形分布,其运动特征完全相同,为了便于直观的展现手指各关节的运动姿态,下文中的图形以左右二等角轴测图的形式展现。

当各关节配置不合适的弹簧时,如图5所示,其抓取形态与人手的抓取形态相悖,会造成不合理的抓取形态;而配置合理的关节弹簧,如图6所示,其抓取形态高度模仿人手抓取动作,因此会有较好的抓取效果。二者的区别在于各指节运动的顺序不同,前者远指节的运动优先于中指节与近指节,造成手指在未触碰物体前已经呈蜷缩状;后者近指节的运动优先于中指节与远指节,使得机械手能在抓取最大区间内完成抓取任务。因此,各关节弹簧的配置影响指节的运动顺序,进而影响手指的抓取特性。

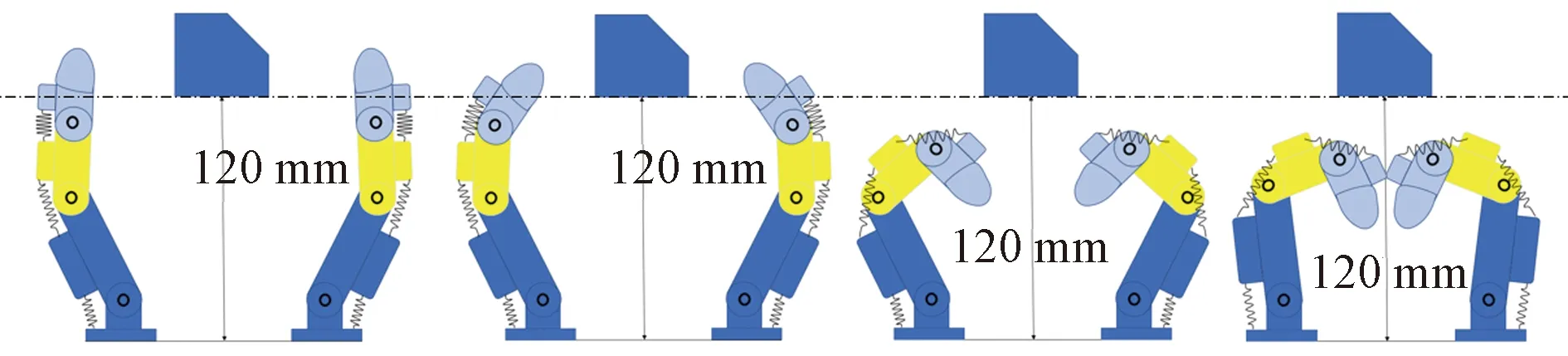
图5 各关节弹簧相同下的抓取姿态图Fig.5 Grasping pose with the same spring in each joint

图6 各关节弹簧合理配置下的抓取姿态图Fig.6 Gripping posture with the right configuration of springs for each joint.(a)Fingertip grip posture diagram;(b) Envelope grip pose map

传统的欠驱动机械手不能主动地在指尖抓取与包络抓取间做出选择。相反,本文研究末端执行器能够通过物体接触被动的进行抓取类型(指尖抓取或包络抓取)的选择,因为能够通过关节弹簧机械地适应物体的形状。当末端执行器通畅的闭合时,如图6(a)所示,远指节、中指节与近指节近似看成一个整体围绕近指关节旋转,直至接触物体完成指尖抓取。如果近指节因与物体接触而停止,如图6(b)所示,中指节与远指节将依次弯曲,从而完成包络抓取任务。

因而各关节线性弹簧的选取必须以手指具有合理的运动特征为依据[20]。忽略手指的质量,为实现如图6所示的运动特征,则需要上述各关节力矩之间满足:

|τ1|≥|τ2|≥|τ3|

(13)

根据式(4)可知关节力矩为:

(14)

当手指结构尺寸参数确定后,各关节的力矩与弹簧刚度成反比,则各弹簧刚度应满足:

K1≤K2≤K3

(15)

根据式(7)可知,关节弹簧刚度越大,手指的负载能力越小,所以式(12)所计算得到弹簧刚度已经是最优刚度区间的最大极限值。为了保证足够的抓取力,需要在上述区间范围内优选弹簧刚度配置。

各关节弹簧的配置将影响末端执行器的抓取空间,尽管以上通过工作载荷已经计算出弹簧的参数区间,但理论上合理的弹簧配置区间有无穷多个[20]。由于线性弹簧是标准件,受其可用性影响,本文以离散配置的方式针对抓取空间进行优化选择。优选4种弹簧刚度,配置如表3所示,通过对单根手指的工作空间进行仿真(见图7),分析发现D配置的抓取空间相较于A、B和C配置最大,因此选择D配置作为各关节的弹簧刚度。

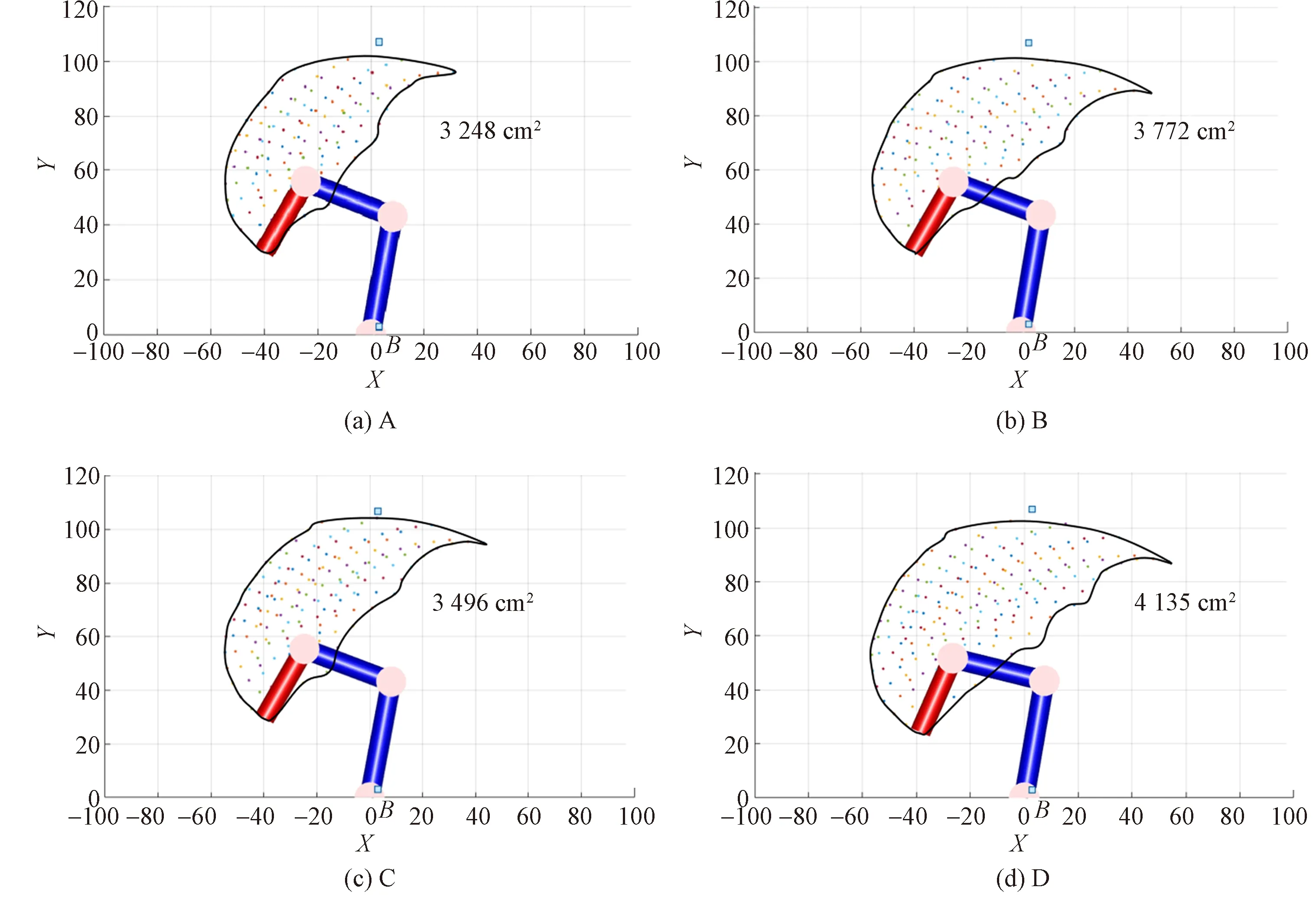
图7 不同弹簧配置下抓取空间图Fig.7 Grab space diagram under different spring configurations

表3 弹簧各配置参数表Tab.3 Table of parameters for each spring configuration N/mm

如果近指关节与中指关节的力矩远大于远指关节力矩,就会出现Birglen所述的“弹出”现象[21],即物体从手指间弹出。而本文研究中各弹簧对关节力矩的影响相较于肌腱力产生的力矩而言,影响甚小;同时远指节的长度在一定程度对被抓物体形成几何约束,因而能够避免“弹出”现象。

4 指尖抓取稳定性分析

现有的抓取稳定性分析较多针对2根手指在二维平面内抓取物体,适用范围有限,而本文研究考虑指尖摩擦,在三维空间分析三指末端执行器的抓取稳定性因素。滚动接触抓取比滑动接触抓取更稳定[17],指尖和被抓物体的滚动运动包括无穷小的平移和旋转,他们都是由于微小的外部干扰造成的。静态平衡是指所有接触力的和等于零。同时,抓握稳定性相当于施加在被抓握物体上的适当刚度,该刚度来自于肌腱的刚度或手指的主动刚度控制[22]。肌腱与弹簧的配合使得机器人手指在一定范围内具有顺应性,其特性类似于弹性机制,通过在触点处构造虚拟弹簧建立指尖等效接触模型,如图8所示,从系统的势能角度分析抓取稳定性的影响因素。

图8 指尖接触等效模型Fig.8 Fingertip contact equivalent model

考虑到3根手指对纱管顶部进行抓取,假设3个指尖进行有摩擦的点接触,利用虚拟弹簧建立指尖接触等效模型如图8所示。Fi是第i个指尖(i=1,2,3)对纱管施加的力,在平衡状态下,F1、F2、F3为内力,3个手指内力相交于点O(内力中心点),以O点建立x、y、z坐标系;ri表示内力中心点到第i个手指到物体接触点的位置向量;θi表示ri与x轴之间的夹角。设定分别正交与各指尖刚性为kxi、kyi、kzi的3组虚拟弹簧,物体在各坐标轴方向x、y、z、ξ、η、ζ上发生微小位移时,各虚拟弹簧kxi、kyi、kzi的压缩量分别为εxi、εyi、εzi。若有外部扰动,在O原点会发生无穷小的位移εi=[εxiεyiεzi]T,规定离开内力中心点的方向为正。

(16)

εyi=-xsi+yci-‖ri‖sici(1-cosξ)+

‖ri‖sici(1-cosη)+‖r‖sinζ

(17)

εzi=z+‖ri‖sisinξ-‖r‖cisinη

(18)

且si=sinθi,ci=cosθi,此时,通过压缩各弹簧而储存在系统中的势能U为:

(19)

式中:ε=[εxiεyiεzi]T;ki=diag[kxi,kyi,kzi];势能U是连续可微的。

当且仅当势能U在平衡状态下局部达到最小值时,抓握是稳定的[23],式(19)中势能U在矩阵形式下的泰勒展开式为:

(20)

势能U局部最小的充分条件是:

①▽U|(0)=0

②H(0)是正定矩阵

根据力平衡原则,条件①总是成立。对于条件②H|(0)是正定矩阵,所以H|(0)的所有特征值都必须是正的。矩阵H|(0)可以表示为

(21)

对H|(0)进行行列变换得到Kx

(22)

而后式(22)可以表示为式(23):

(23)

系统稳定的充分必要条件是2个子矩阵Kx1、Kx2分别正定。因每个指尖设定的虚拟弹簧存在一定的下限,因此给出各参数指尖的配比。

kcx=kx1+kx2+kx3

(24)

knxi=kxi/kcx(i=1,2,3)

(25)

kcy=ky1+ky2+ky3

(26)

knyi=kyi/kcy(i=1,2,3)

(27)

Fc=‖F1‖+‖F2‖+‖F3‖

(28)

Fni=‖Fi‖/Fc(i=1,2,3)

(29)

rc=‖r1‖+‖r2‖+‖r3‖

(30)

rni=‖ri‖/rc(i=1,2,3)

(31)

为使Kx1>0,则必须

(32)

同理可求得当Kx2>0,则必须

(33)

式中:A=a1a2-c2,B=a1b2+a2b1

(34)

(35)

(36)

(37)

kcz>kcz2

(38)

因此满足以下3个公式:

kcx>0

(39)

(40)

kcz>kcz2

(41)

对于3点对心抓取,无论末端执行器是否是欠驱动,力闭合对实现稳定抓取起着至关重要的作用[24]。前一节分析手指刚度对抓取系统稳定性的影响,同时各手指合力中心位置与系统抓取稳定性也存在某种函数关系,但在式(39)～(41)中的关系很难理解。每一个指尖只能产生一个接触点,为此利用3个接触点构建抓取三角形如图9所示。F1、F2、F3为3个指尖的抓取力,点c为抓取内力的合力点,r为纱管的端部半径,因此,根据以上的相关推导,给定r=1 cm,Fc=1 N,定量分析手指内力中心位置对抓取系统稳定性的影响。

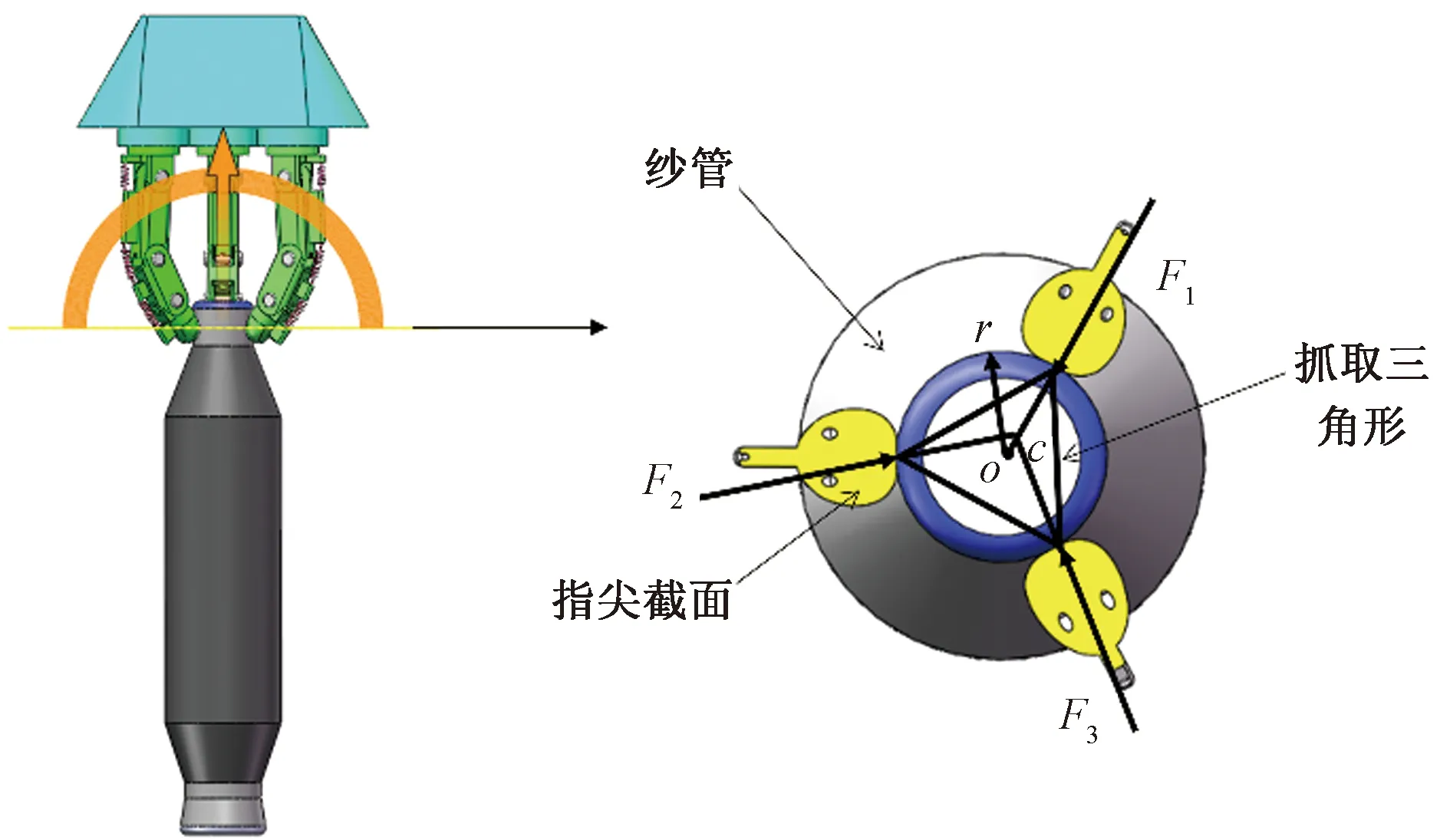
图9 抓取纱管截面图Fig.9 Cross section of gripping bobbin

从图10抓取刚度下限分布可以看出,方向从抓握三角形外接圆的圆心到手指接触点,内力中心位置与ky、kz的下限值之间的关系,随着内力中心点的位置接近手指接触点,其ky、kz的下限值剧增,在各手指接触点附近达到无穷大。在内力中心点位于抓取三角形外接圆的圆心时,其抓取系统受到的扰动最小,抓取最稳定。采用模块化思想设计的手指,当其呈正三角形分布,较容易实现抓取合力位置的中心化,因而抓取较为稳定。

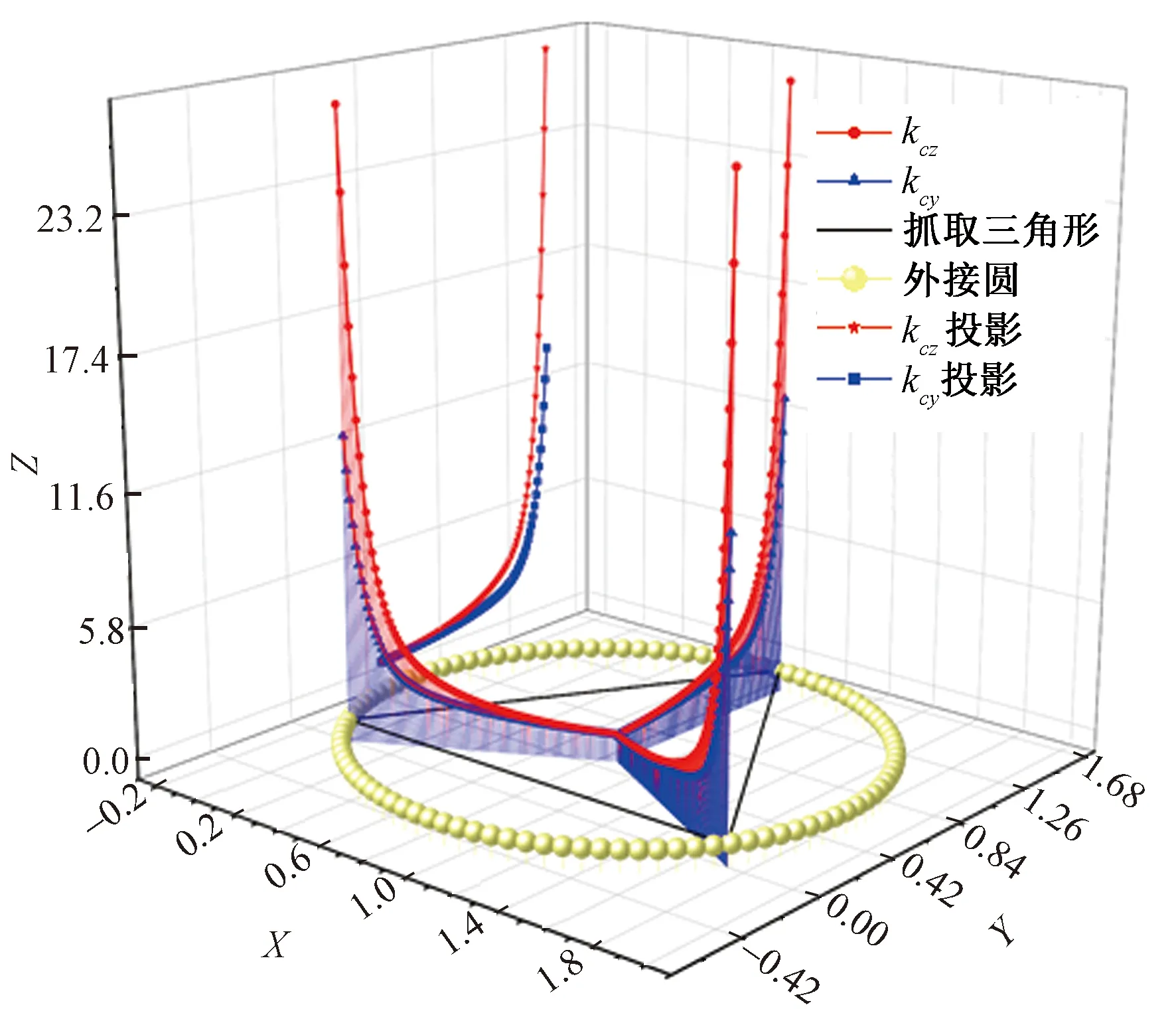
图10 抓取刚度下限值分布Fig.10 Distribution of lower limit of grasping stiffness

从式(39)～(41)可看出,当手指抓取内力Fc越大且物体的半径rc越小,则刚度矩阵的特征值越大,抓取系统的稳定性越高。但相对于末端执行器而言,手指的指尖半径曲率越大,则刚度矩阵的特征值越大,抓取系统越稳定,抗干扰性能越强。

5 指尖设计

由于在指尖抓取期间发生摩擦接触的滚动约束,不同形状组合的过渡点必须是切点[25]。从仿生学的角度研究,人类手指的轮廓由椭圆形和矩形图案组成。考虑到手指尖端到手指表面的圆滑过渡,则有必要使得矩形与椭圆形相切,但二者相切的程度将影响抓取的稳定性。分析式(40)可知,为了达到较高的稳定性抓取状态,则需要手指指尖圆弧的曲率在允许范围内尽可能大。为此,将手指关节轴中心位置作为椭圆的一个焦点,手指的高度作为椭圆的短轴,远指节的长度即为椭圆长轴左端点到右焦点的距离,如图11(a)所示。

图11 指尖形状图Fig.11 Fingertip shape map.(a)Front view of fingertip;(b)Left and right isometric axonometric drawing

椭圆标准方程为:

(42)

已知b=13,a+c=30,根据椭圆的固有性质:c2=a2-b2即可求得,a=17.82,c=12.18,可得椭圆方程为:

(43)

结合人手指尖生物特征,使用椭圆曲线作为指尖轮廓曲线,通过放样建立指尖三维结构模型,如图11(b)所示。

6 试 验

结合稳定性分析与指尖设计,采用3D打印技术制作仿生末端执行器,对多尺寸纱管进行一系列抓取试验,验证抓取性能。本文控制系统包括驱动器、单片机和步进电动机等主要部件,驱动器对脉冲信号进行分配与放大,进而将使得步进电动机接受指令进行相应运动。试验中选取聚乳酸纤维PLA作为打印材料,其具有较好的热熔性能,能够满足结构设计中的机械强度要求。软手指接触的指尖抓取不仅力闭合而且稳定,所以用软橡胶覆盖指尖是获得稳定抓取最简单的方法[26]。指尖(橡胶)与物体之间接触点处的摩擦因数范围为0.2～1.6,摩擦因数选定为0.6。选择42HS4148作为步进电动机进行仿生末端执行器的驱动,TM32F103系列单片机,TB6600步进电动机驱动器。

为了实现静态平衡状态,手指各接触点处的摩擦力必须抵消被抓物体的重力,力平衡方程可以提供为:

G=3F1μcosσ

(44)

式中:G表示被抓物体的重力,N;F1为指尖接触力,N;μ是摩擦因数,μ=0.6;σ是接触力与水平面的夹角,(°),在抓取过程中其夹角接近于零。考虑到步进电动机的转矩与绳轮摩擦的消耗,F1≪8 N。理论上可以抓取物体的最大质量为1.44 kg,而本文试验中被抓物体的质量仅在23～110 g之间,因此可以满足抓取力的条件。

为了验证该末端执行器的抓取稳定性,依次对不同尺寸纱管进行抓取试验,为进一步验证该末端执行器的自适应性,还对网球进行抓取试验。试验过程可以分为4个阶段:

阶段一:末端执行器按照规划路线移动到被抓物体上方,抓取物体后上升到至离地5 cm。

阶段二:随后末端执行器在其水平方向上以10 mm/s2的加速度加速运行3 s 。

阶段三:随后保持30 mm/s的速度运行1 s。

阶段四:然后以15 mm/s2的加速度减速运行2 s,到达预定位置。

在每一个阶段完成后,如果被抓物体不脱落,记一次成功,每组试验重复30次,图12为部分抓取试验图,试验结果统计如表4所示。

图12 指尖抓取试验图Fig.12 Grab object test diagram

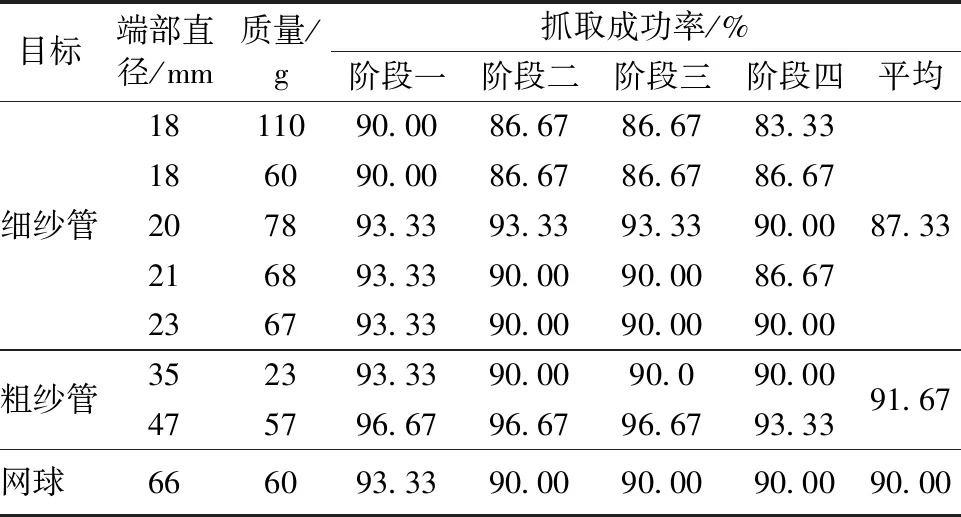
表4 指尖抓取成功率Tab.4 Capture success rate

抓取试验过程分为4个阶段,而阶段四的成功率代表该末端执行器对特定尺寸纱管抓取30次且纱管不脱落的概率。由表4可知,该末端执行器的抓取成功率基本在83%以上,5种细纱管的平均抓取成功率为87.33%,2种粗纱管的平均抓取成功率为91.67%,网球的抓取成功率为90%。

纵向对比分析,随着纱管端部直径(18～47 mm)的增加,其抓取成功率呈增大趋势,抓取直径为47 mm粗纱管的成功率高达93.33%。对网球进行抓取试验成功率也能达到90.00%,表明该末端执行器具备较好的自适应性。

横向对比分析可知,抓取过程依次经过4个阶段,前一阶段的抓取成功率将会影响后一阶段的抓取成功率,因此其抓取成功率逐渐减小是合理的。相对于阶段二、三和四而言,阶段一被抓物体脱落的次数较多,其抓取失败的原因在于纱管的放置位置偏离了预定位置,造成末端执行器指尖抓取中心不能与纱管端部中心在同一竖直轴线上。因试验平台上没有设置定位纱管的卡槽,而实际作业环境中会有底槽用于固定和定位纱管,以上情况即可避免,抓取成功率也会相应提高。与纱管相比,网球的外部曲率变化较大,三指对心抓取高度将影响抓取成功率,但网球的表面较为粗糙,一定程度上弥补前者精度要求。在阶段二、三和四中,在加减速过程中纱管与网球出现脱落的情况甚少,表明该末端执行器具有较好的抗干扰能力和稳定性。

为了进一步验证该末端执行器的抓取性能,对直径110 mm、质量750 g的大纱筒进行包络抓取,如图13所示,末端执行器能够按照期望的运动特性完成抓取任务。

图13 包络抓取纱筒各阶段图Fig.13 Diagram of the various stages of envelope gripping yarn cylinders

7 结 论

采用肌腱式欠驱动原理设计一款面向纱管抓取的仿生末端执行器,3根手指呈正三角形分布,能够实现对不同尺寸纱管的自适应抓取。基于人手抓取机制,规划手指内部肌腱传输路径。3根手指采用模块化设计思想,结构简单便于加工与安装。关节弹簧不仅能够使手指进行复原,而且影响手指运动特征。通过合理的弹簧配置使得机构具备被动顺应性,实现抓取策略(指尖抓取与包络抓取)的被动切换。以刚度矩阵的特征值为指标评价抓取稳定性,进而优选指尖的结构参数。基于力的合成理论,定量分析抓取稳定性,同时进一步验证手指布局的合理性。

利用3D打印技术制作仿生末端执行器样机,在不同试验环境下,对直径18～47 mm的纱管、直径66 mm的网球进行自适应抓取测试,结果表明,指尖抓取细纱管、粗纱管、网球的平均成功率分别达到87.33%、91.67%、90.00%,也能包络抓取直径110 mm纱筒,验证了该仿生末端执行器能够稳定抓取多尺寸纱管。