车-桥随机系统行车安全指标极值预测的自适应代理模型方法
2023-10-18王力东刘汉云蔡春声
张 迅, 韩 艳, 王力东, 刘汉云, 蔡春声
(1.长沙理工大学 土木工程学院,长沙 410114; 2.东南大学 交通学院,南京 211189)
为保证线路的平顺性及减少耕地占用,我国高速铁路常采用“以桥代路”的建设方式。据统计我国高速铁路网中桥梁平均占比大于50%,其中广珠铁路桥梁占比高达94.2%[1]。受运营环境、上座率、施工或制造误差等因素影响,列车在桥上运行时的动力响应表现出明显的随机性。目前,多随机因素影响下的桥上列车运行安全越来越受到关注[2]。
蒙特卡罗法(Monto Carlo method, MCS)是车-桥系统随机振动研究最基本的一种方法[3],它通过大量样本计算得到车-桥系统动力响应的统计信息。尽管MCS简单易行,但其所需样本容量大,效率低。为减少样本数量,部分学者提出了方差缩减技术,包括子集模拟[4]、方向模拟[5]和重要性抽样[6]等。此外,多种高效随机振动分析方法,如虚拟激励法[7]、概率密度演化法[8]和时域显式解法[9]等也被用于解决车-桥系统随机振动问题,提高了计算效率。尽管如此,当考虑行车安全等小概率事件时,基于理论模型的车-桥随机振动分析依然效率偏低[10]。
近年来,随着机器学习的快速发展,代理模型被逐渐应用于车-桥系统随机振动研究中[11]。代理模型是指利用一定数量训练样本建立的数学模型,该模型可以近似表征物理模型。目前常用的代理模型包括克里金模型、支持向量机、径向基函数(radial basis function, RBF)和神经网络等。代理模型的计算速度很快,与物理模型相比,其计算成本几乎可以忽略不计[12]。在利用代理模型进行车-桥系统随机振动分析的过程中,计算成本主要花费在训练样本的计算上。因此,利用何种采样方法,能够在不增加训练样本数量的情况下提高代理模型预测精度是研究的关键[13]。
目前常用的采样方法可分为一次性采样(one-shot sampling, OS)方法和自适应采样(adaptive sampling, AS)方法。一次性采样是在建立代理模型之前,一次性确定所有样本点的数目和位置,包括随机抽样、拉丁超立方抽样和正交设计等[14]。虽然该类采样方法能尽可能的减小样本点集的偏差,但无法根据目标函数合理地分配样本点的位置,导致训练集样本信息重复、利用率不高。同时,该类采样方法也无法事先确定合适的训练样本数量。自适应采样方法则是先利用少量的初始样本点构建代理模型,进而利用代理模型和准则函数在候选样本点集中选出新的样本点,并将其添加至训练集中,用于更新代理模型。如此循环迭代,直至代理模型满足精度要求。
目前已有学者将自适应代理模型应用于结构随机分析中。Zheng等[15]基于U准则函数建立了自适应克里金代理模型,预测了三跨连续梁最大静位移。然而,U准则函数的局限性较大,仅适用于能够预测方差的代理模型,这严格限制了该方法在其他代理模型(如RBF、BP神经网络)中的应用[16]。Xiang等基于加权采样法,建立了自适应神经网络代理模型,计算了大型钢箱梁斜拉桥的失效概率。然而,该研究建立的代理模型仅能保证结构失效位置附近的预测精度,而不是整个概率空间内的预测精度,即全局预测精度。Zhou等[17]利用Mo等[18]提出的准则函数,建立了自适应高斯过程回归代理模型,预测了多层框架结构动力响应的等价极值量,提高了代理模型的全局预测精度。此外,尽管目前已有学者将代理模型应用于车-桥系统随机响应预测[19-20],并分析了不同代理模型的预测效果,但大都基于一次性采样方法建立代理模型。
为提高车-桥耦合系统行车安全指标极值预测精度,本文提出了一种自适应代理模型方法。以轮重减载率极值预测为例,建立了车-桥系统自适应代理模型和一次性采样代理模型,对比分析了两种代理模型的训练样本点分布情况,并结合理论模型计算结果,验证了所提方法的预测精度和优越性。
1 方法框架
本文提出了一种车-桥系统自适应代理模型构建方法,用于行车安全指标极值预测。该方法主要包括车-桥耦合振动理论模型、代理模型和自适应采样方法三个部分。其中,车-桥耦合振动理论模型用于生成当前训练集对应的车辆动力响应;代理模型用于建立车-桥系统中随机变量与行车安全指标极值之间的关系;自适应采样方法用于在候选样本点集中选出新的样本点,更新代理模型,提高预测精度。图1给出了车-桥耦合系统自适应代理模型构建框架。

图1 车-桥耦合系统自适应代理模型构建框架Fig.1 Construction framework of adaptive surrogate model for train-bridge system
1.1 车-桥耦合振动模型
车-桥耦合系统由车辆和桥梁子系统组成,并通过轮轨接触关系相互联结。本文分别采用多体动力学和有限元方法建立车辆和桥梁子系统动力学模型,采用线性赫兹接触弹簧模拟轮轨接触,最终可建立如下所示车-桥耦合振动方程[21]
(1)

受上座率、制造误差以及列车运营环境和季节等因素影响,车体质量、悬挂刚度和阻尼等参数存在随机性。因此,车-桥耦合振动方程(式(1))可以改写为
ΓFr(Θ,t)
(2)
式中:Θ=[Θ1,Θ2…Θd]表示车-桥系统中的随机变量,例如车体质量、悬挂刚度、悬挂阻尼和车速,d表示随机变量的个数;Γ表示变换矩阵,用于定义系统中受轨道不平顺激励的自由度。在给定的初始条件下,式(2)的解答存在、唯一且依赖于随机变量Θ。
对于车-桥耦合振动系统而言,通常采用行车安全指标极值来评判列车的运行安全。由于一列车包含多节车厢,每节车厢又包含多个车轮,且列车行驶过程中任何一个车轮的行车安全指标都可能超过规范限值,因此,列车行车安全指标极值W(Θ)需通过下式求得
(3)
式中:Z(Θ,t)={Zj(Θ,t),j=1,2,…,M},Zj(Θ,t)表示第j个车轮的行车安全指标,M表示列车车轮的总数;T表示列车通过桥梁的时间。
1.2 径向基函数(RBF)

(4)
式中:θ表示基于选点方法得到的样本点;ε表示近似误差;ξ表示代理模型中需要确定的待求系数。

(5)
其中,
P(θ)=p·c=
(1,θ1,θ2,…,θd)(c1,c2,…,cd,cl)T
(6)

(7)

1.3 自适应采样方法
通过式(7)可知,待求系数向量λ和c与训练样本{[θi,W(θi)],i=1,2,…n}有直接关系,因此,采样方法会显著影响代理模型的预测精度。本文提出的自适应采样方法主要包括样本点集的生成和基于准则函数的新样本点选取两个方面。
(1) 样本点集的生成
本文基于GF偏差最小化准则生成初始样本集、候选样本集和验证集[22]。其中,GF偏差的表达式如下
(8)
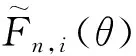
(9)

生成样本点集的具体步骤:首先,在d维单位超立方体中生成Sobol点集U={uq=(uq,1,uq,2,…,uq,d),q=1,2,…,n},并对Sobol点集U进行变换,得到点集Θ={θq=(θq,1,θq,2,…,θq,d),q=1,2,…,n}
(10)

i=1,…,d
(11)

i=1,…,d
(12)

(2) 准则函数
本文基于Mo等提出的准则函数来确定新的样本点。该准则函数包含全局探索和局部开发两个部分。其中,全局探索部分用于发现样本点稀疏的区域,该部分采用样本点之间的欧氏距离来度量,具体表达式如下
(13)
式中,θt,nr表示当前训练集Θcur中与候选样本θ距离最近的样本点。


(14)

Rrem(θ)=|W(θ)-t(θ,θt,nr)|
(15)
为动态调节全局探索和局部开发所占权重,定义如下形式的准则函数
(16)
式中,ω(θ)表示权衡因子,通过式(17)计算
(17)
式中,Lmax表示候选样本点集中任意两个样本点之间距离的最大值。
在计算了所有候选样本点的准则函数J(θ)后,可通过下式确定新的样本点
(18)
通过分析式(16)和(17)可知,在刚开始建立代理模型时,当前训练集中样本数量较少,导致Dmin(θ)值较大,权衡因子ω(θ)较小,全局探索部分占优。随着迭代次数的增加,当前训练集中样本数量逐渐增加,权衡因子ω(θ)逐渐变大,局部开发部分逐渐占优。
采用如下所示当前误差(present square error, PSE)来度量当前迭代步中构建的代理模型的精度
(19)
从而,设计迭代终止条件如下所示
(20)
式中:PSE的上标表示迭代步数;εthr表示设定的当前误差阈值。由于在自适应采样过程中,PSE会出现显著的震荡现象,因此本文要求当PSE连续4次小于当前误差阈值εthr,以保证终止条件的稳定性。
2 自适应代理模型构建流程

(1) 基于GF偏差最小化准则生成初始样本点集Θinit和候选样本点集Θcand(式(10)~(12))。
(2) 利用车-桥耦合系统理论模型(式(2)~(3))计算初始样本点集Θinit对应的轮重减载率极值Winit=W(Θinit),进而将(Θinit,Winit)设置为当前训练集(Θcur,Wcur)。

(4) 计算准则函数J(θ)(式(16)),确定新样本点θnew(式(18)),计算轮重减载率极值的理论值Wnew=W(θnew)。
总体组是铁路勘察设计院最基本的生产单元,鉴于总体在项目推进过程中发挥着最基础、最完整、最重要的统筹协调和把关作用,总体是团队运作的“领军人”、信息传递的“中间人”、项目控制的“关键人”、形象展示的“代言人”。这个表述远远高过设计院规定的岗位职责,明确了总体既负总责,又抓落实,还当代言的角色定位。

3 算例分析
本章分别采用移动车轮加簧上质量过简支梁桥和车-桥耦合系统竖向振动模型来验证所提方法的有效性。考虑到对于某一特定桥梁,轨道不平顺为确定值,因此本节采用中国高速铁路无砟轨道谱生成一条轨道不平顺时域样本作为激励输入,建立考虑车辆参数随机的轮重减载率预测代理模型。根据参考文献[14],本研究通过均方根误差RMSE评价代理模型的预测精度,其表达式如下
(21)
式中:θval,i表示第i个验证样本;m表示验证集样本的总数。
3.1 移动车轮加簧上质量过简支梁桥
本节考虑2自由度车辆通过32 m简支梁桥,如图3所示。其中车辆采用车轮加簧上质量模型,桥梁采用平面欧拉梁单元有限元模型,轮轨接触采用目前常用的线性赫兹接触模型,其轮轨接触刚度通过切线斜率法获得的[23]。为验证本文所提方法在全局探索和局部开发方面的能力,选取两个工况进行分析。工况1:车辆悬挂刚度和悬挂阻尼随机,并且车速恒定为300 km/h;工况2:车体质量和车速随机。Yu等认为上述随机变量服从正态分布,参数取值如表1所示。车-桥系统其余参数设置为:轮对质量mw=1.2 t,轮轨接触刚度kh=1.04 MN/m,桥梁弹性模量E=3.55×1010Pa,密度ρ=2.5×103kg/m3,截面抗弯惯性矩I=10.81 m4,截面面积A=8.66 m2。
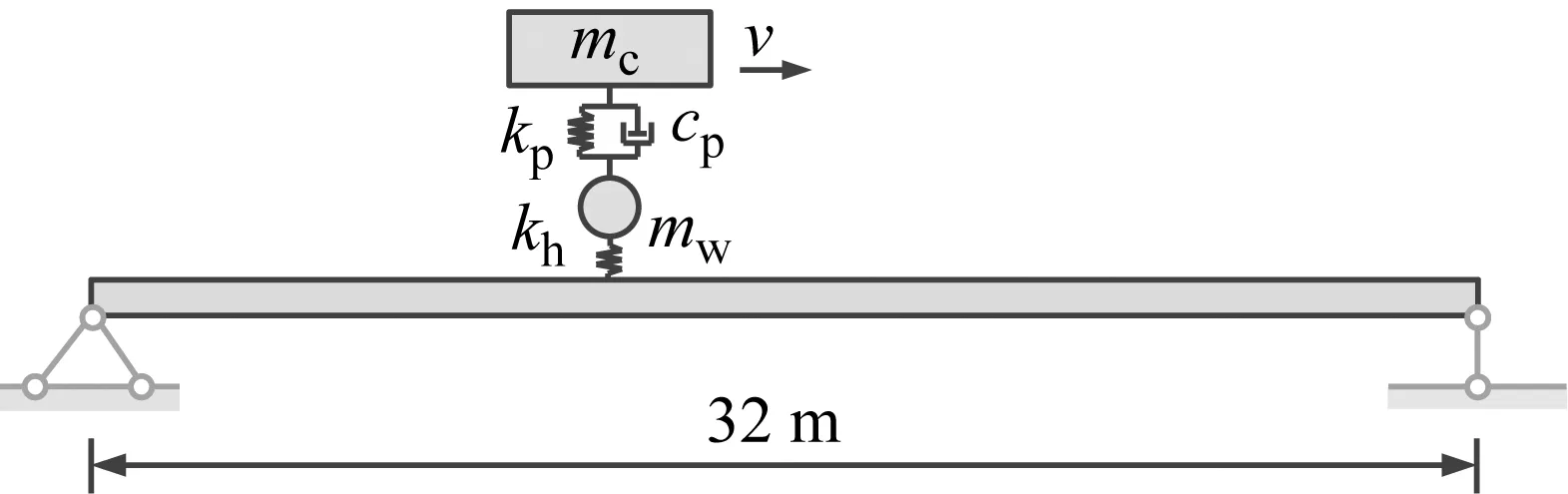
图3 移动车轮加簧上质量过简支梁桥Fig.3 Moving wheel and sprung mass passing through simply supported beam bridge

表1 移动车轮加簧上质量过简支梁桥模型随机参数Tab.1 Random parameters of a moving wheel and sprung mass passing through a simply supported beam bridge
图4给出了代理模型误差随当前训练集样本数目的变化趋势,此处当前误差阈值εthr根据经验设置为0.002。该误差较小,当代理模型满足该误差阈值时,其预测结果足以满足行车安全评估的要求。图中AS和OS分别表示采用自适应采样和一次性采样方法建立的代理模型。可以看出,随训练样本点数目的增加,两种代理模型的RMSE均呈下降趋势,但自适应代理模型的预测精度明显优于一次性采样代理模型。以工况2为例,当自适应代理模型满足收敛条件时,自适应代理模型和一次性采样代理模型的RMSE分别为1.4×10-3和2.5×10-3,前者较后者的预测精度提高了1.8倍。这表明,自适应采样方法能够在不增加样本数量的情况下,显著提高代理模型预测精度。

(a) 悬挂刚度和阻尼随机(工况1)

(b) 车体质量和车速随机(工况2)图4 代理模型误差随样本数目变化趋势Fig.4 Variation trend of surrogate model error with sample number
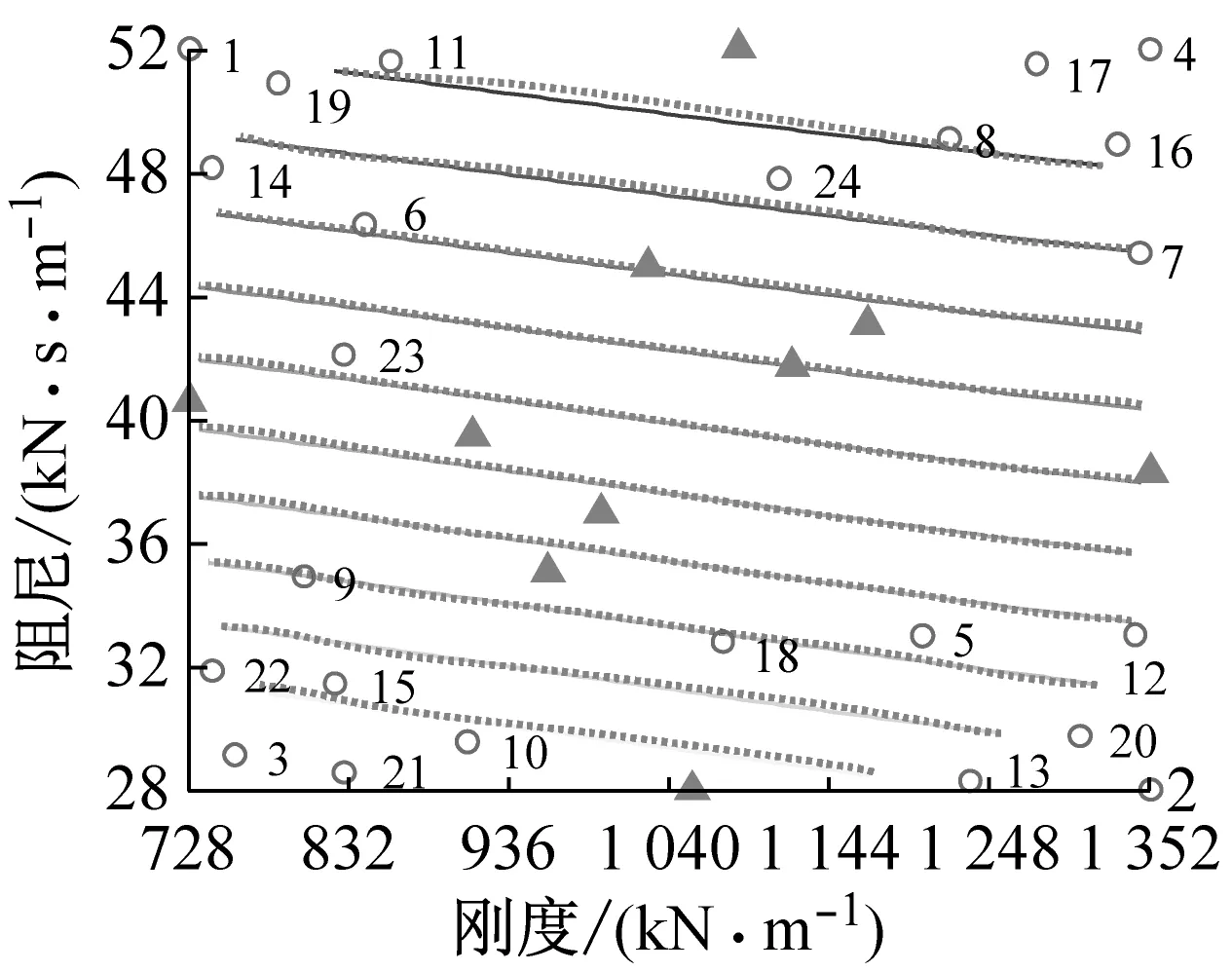
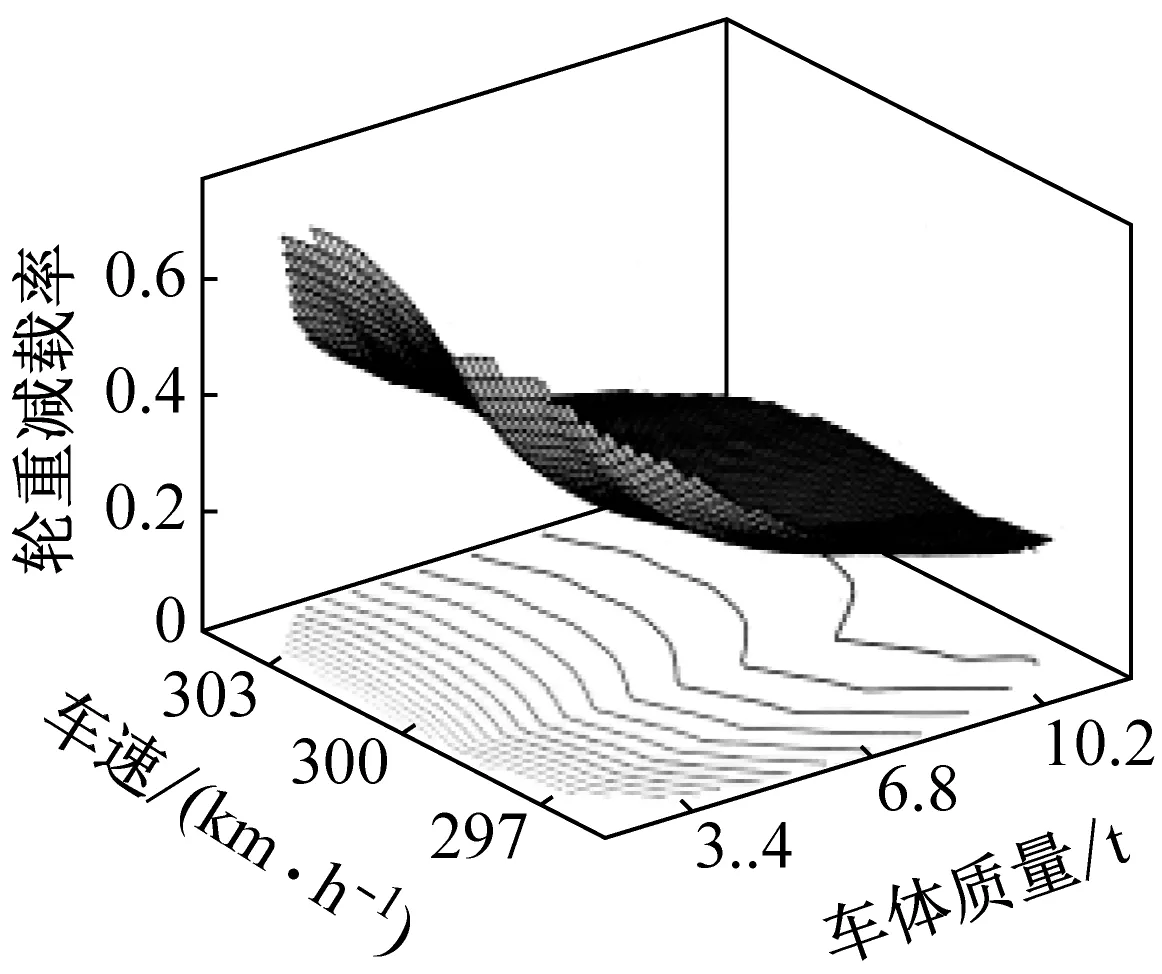
图5(a)和(d)给出了两个工况下轮重减载率极值的变化趋势。可以看出,轮重减载率随悬挂刚度和悬挂阻尼基本呈线性变化(工况1),而随车体质量和行车速度呈明显非线性变化(工况2),两种工况的目标函数存在显著差别。结合图4对自适应代理模型进行分析,由于工况1的目标函数较为简单,仅需33个训练样本就能满足终止条件,而工况2的目标函数相对复杂,需要102个训练样本才能满足终止条件。这说明尽管采用同样的车-桥耦合振动模型,但由于目标函数的复杂程度不同,导致建立代理模型时所需的训练样本数量也不同。本文提出的自适应采样方法能够逐次选出新样本点,直至代理模型预测精度满足设定目标,很好地解决了一次性采样法难以确定合适的训练样本数量的问题。另外,需要说明的是,在普通个人计算机上建立一次代理模型并利用准则函数确定下一个样本点所需的时间仅为0.11 s,这与计算一个车-桥耦合振动样本所需的时间相比完全可以忽略不记。因此,虽然建立自适应代理模型所需的样本点要更新迭代,但这对计算效率的影响甚微。

(a) 理论值(工况1)

(b) 一次性采样(工况1)
(c) 自适应采样(工况1)
(d) 理论值(工况2)

(e) 一次性采样(工况2)

(f) 自适应采样(工况2)图5 轮重减载率变化趋势及样本点分布图Fig.5 Variation trend of wheel load reduction rate and distribution of sample points
图5(b)、(c)和(e)和(f)分别为两种工况下不同代理模型训练样本点的分布情况,图中数字表示新样本点的发现顺序。对比图5(b)和(c)可以看出,自适应代理模型的等高线与目标函数吻合良好,而一次性采样代理模型的等高线与目标函数具有较大差别,表明自适应代理模型的预测精度远高于一次性采样代理模型。这是由于一次性采样未考虑目标函数的具体形式,样本点大多集中在均值附近,呈正态分布(图5(b)),未能合理分布有限的训练样本点,导致训练样本点利用率不高。同时,根据图5(c)所示新样本点的发现顺序可以看出,自适应采样方法能够有效的识别训练样本点稀疏区域,具有良好的全局开发能力。
通过图5(d)可以看出,随着车体质量的降低,轮重减载率逐渐增加,并且车体质量越小变化越显著。同时,在车速为298.8 km/h附近,轮重减载率明显减小。对比图5(e)和(f)可以看出,一次性采样代理模型在样本集中区域的预测精度较高,但在样本稀疏区域预测精度较差,而自适应代理模型在整个样本空间内均有良好的预测精度。通过图5(f)可以看出,自适应代理模型的样本点在车辆质量较小的区域和车速为298.8 km/h附近(图5(f)虚线位置)较为密集,其他区域较为稀疏。这表明,自适应采样方法有效的识别了目标函数非线性较强区域,并对该区域进行了样本点加密,体现了自适应采样局部探索的能力。
3.2 车-桥竖向耦合振动模型

图6 轨道-桥梁模型Fig.6 Track-bridge model

(a) 主梁

(b) 桥墩图7 桥梁截面示意图Fig.7 Schematic diagram of bridge

图8 车辆模型Fig.8 Model of vehicle

表2 车辆随机参数Tab.2 Random parameters of vehicle
图9给出了代理模型误差随当前训练集样本数目的变化趋势,此处当前误差阈值εthr设置为8×10-4。可以看出,自适应代理模型的预测精度始终高于一次性采样代理模型。在样本数目达到203个时,自适应代理模型满足终止条件。此时,自适应代理模型和一次性采样代理模型的预测误差分别为0.64×10-3和1.6×10-3,即,前者的预测精度是后者的2.5倍。图10为预测值和理论值的对比图,可以看出自适应代理模型较一次性采样代理模型更靠近理论值。在轮重减载率较小和较大的区域,一次性采样代理模型的预测值与理论值偏差更大。这是由于一次性采样的训练样本大多集中在随机参数均值附近,离均值较远的位置样本点较少,预测精度较差。
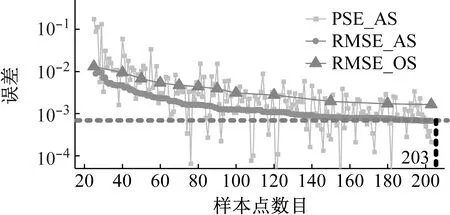
图9 代理模型误差随样本数目变化趋势Fig.9 Variation trend of surrogate model error with sample number

图10 预测值和理论值对比Fig.10 Comparison between predicted value and theoretical value
图11给出了代理模型预测值的统计信息。图11(a)为基于两种代理模型预测的轮重减载率极值箱形图。可以看出,一次性采样代理模型在轮重减载率较小的区域出现大量异常值,这与理论模型的计算结果差异较大,而自适应代理模型的预测结果与理论模型较为接近。图11(b)和(c)分别为概率密度函数和累计分布函数,可以看出,在轮重减载率较大和较小的区域自适应代理模型的预测结果与理论值更为接近,这与图10的分析结果一致。
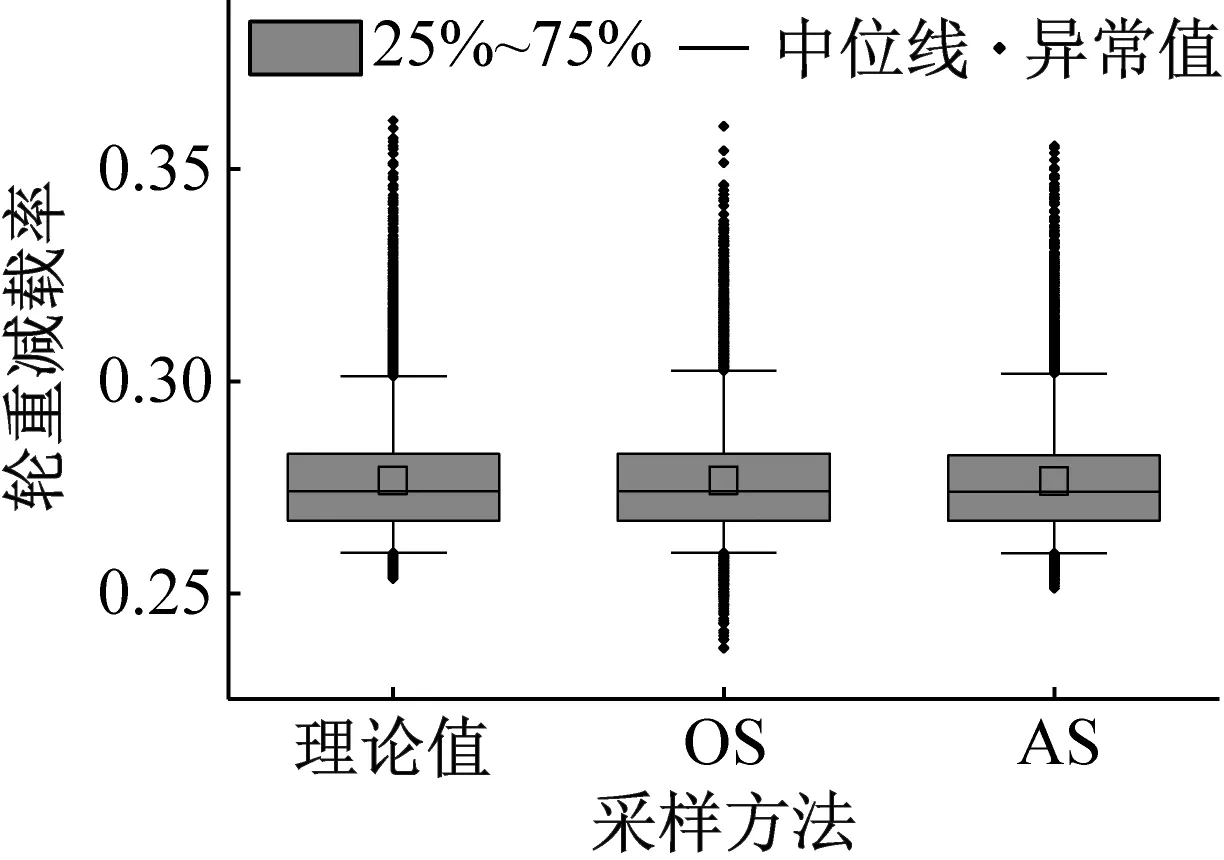
(a) 轮重减载率极值

(b) 概率密度函数

(c) 累计分布函数图11 代理模型预测值统计图Fig.11 Statistical graph of predicted value of surrogate model
4 结 论
本文提出了一种车-桥耦合振动系统行车安全指标极值预测的自适应代理模型构建方法。以移动车轮加簧上质量过简支梁桥和车-桥耦合系统竖向振动模型为例,分别建立了轮重减载率预测的自适应代理模型和一次性采样代理模型,并对比分析了两种代理模型的训练样本点分布情况及预测精度,得到如下结论:
(1) 自适应代理模型能够有效提高轮重减载率极值预测精度。就移动车轮加簧上质量过简支梁桥和车-桥耦合系统竖向振动模型而言,自适应代理模型较一次性采样代理模型的预测精度分别提高了1.8倍和2.5倍。
(2) 一次性采样代理模型仅在均值附近预测精度较高,而自适应代理模型在整个样本空间内均有良好的预测精度。这是因为自适应代理模型具有良好的全局探索和局部开发能力,能够发现训练集样本点稀疏区域和目标函数强非线性区域,并对这些区域进行样本点加密,从而提高代理模型在轮重减载率较大和较小区域的预测精度。
(3) 自适应代理模型通过循环迭代的方式逐一增加训练样本的数量,直至当前误差满足终止条件,很好地解决了一次性采样法难以确定合适的训练样本数量的问题。以本文车-桥系统竖向随机振动计算为例,达到预测精度所需样本数量为203个。
