基于熵权法的含间隙和柔性的机构定量分析方法及应用

2023-10-18潘佳煊钱孟波孙福兴

振动与冲击 2023年19期

潘佳煊, 钱孟波, 孙福兴, 虞浪, 陈强

(浙江农林大学光机电工程学院,杭州 311300)

并联机构具有整体结构稳定、精度高和承载能力大的优点,广泛应用于多个领域。将2-RR&2-PR并联机构作为农业中谷物清选振动筛的主要机构,相比于传统振动筛,使筛面获得空间多维运动,加快物料的散开速度,提高透筛效率,增加使用寿命。

在以往的振动筛系统运动特性研究中,学者们都将整个振动筛系统简化为一个多刚体系统[1-2]。这种方法忽视了系统中构件的材料弹性属性,在实际工作过程中相应的构件会产生弹性变形,并且由于机械加工制造和机器在高速情况下工作而造成的摩擦磨损等因素产生间隙,以上都可能会影响机构运动时的稳定性和使用寿命。因此,有必要综合考虑间隙与构件柔性对机构动态特性的影响,并量化对机构各指标的影响程度,从而提供理论参考。

近年来,学者们在对机构运动特性分析中考虑并引入了间隙或构件柔性。Flores[3]建立了连续接触碰撞力模型,并对具有间隙的平面四杆机构进行了分析。Bai等[4-5]提出了一种改进的非线性连续接触力混合模型,以四连杆机构为对象分析了转动关节间隙的平面机械系统的运动特性。Qian[6]等用带间隙的三维平移关节进行了实验,以揭示滑道和滑块之间的相对运动特性,利用Poincaré映射和Lyapunov指数验证了带间隙平移关节中存在混沌行为。Erkaya等[7]提出含间隙四连杆机构的动力学模型,为了控制连杆的柔性改变连杆的截面尺寸,来研究柔性对间隙机构动态特性的影响。孙杰等[8]提出一种含间隙铰接的航天器刚柔耦合模型建立与控制方法,来减缓间隙对航天器动态特性造成的影响。

信息熵作为一种非常重要的非线性分析方法,被广泛运用于计算机、机械、数学、金融等领域。基于信息熵提出了很多相关的方法,如交叉熵[9]、功率谱熵[10]、基于EEMD的奇异谱熵[11]等。Qian等[12]运用信息熵理论,提出了一种含间隙机构动力响应非线性分析的新方法,对圆柱间隙关节机构的非线性行为进行定量分析。熵权法是一种基于信息熵理论的目标值分配方法,关于熵权法的研究,林巨广等[13]采用熵权法对轴承故障进行诊断,取得了较好的故障识别效果。蒋荣超等[14]提出基于熵权法的结构综合贡献系数计算方法,以此为评价指标筛选出对悬架性能影响较大的结构参数作为整车性能匹配优化的设计变量。

现有基于信息熵理论对含间隙机构运动特性非线性定量分析研究国内外鲜有人做,本文基于熵权法对含间隙和构件柔性的并联机构进行非线性定量分析,以2-RR&2-PR并联机构为研究对象,首先利用ADAMS二次开发功能,通过Fortran语言自主编写间隙接触力子程序,加载到ADAMS函数求解库中,建立了考虑间隙的机构动力学模型,然后开展考虑间隙和构件柔性的机构运动特性仿真,通过仿真数据对比分析在不同条件下对机构运动特性的影响,最后采用Lyapunov指数验证其运动非线性,在此基础上提出一种基于熵权法的非线性定量分析新方法,评估间隙和构件柔性对机构非线性的影响程度,对机构进行更准确地描述。

1 含间隙2-RR&2-PR并联机构动力学模型与分析模型

1.1 并联机构描述

2-RR&2-PR并联机构的机构示意图如图1所示,该机构由动平台、静平台和两条支链组成。其中两条支链上,A1、A2、A3、A4、A5、A6为6个转动副,B1、B2为2个移动副。整个机构可视为对称布置、同步驱动的两曲柄滑块机构A1A3A5B1与A2A4A6B2,因其连杆A3A5、A4A6运动规律一致,故可将A3A4A6A5视为同一刚体,即动平台。通过2个移动副的驱动,实现动平台的上下振动,从而实现整个机构的运动。机构的模型参数如表1所示,本节先考虑转动副A1处的间隙,并将构件A3A5和A4A6柔性化处理。

图1 含间隙和柔性杆的2-RR&2-PR并联机构示意图Fig.1 Schematic diagram of 2-RR&2-PR parallel mechanism with clearance and flexible rod

表1 机构构件参数Tab.1 Mechanism component parameter

1.2 含间隙旋转副的接触力模型

机构在运动过程中,元素之间会相对运动,在运动副处往往会因为磨损产生间隙,间隙的存在会导致元素间的接触和碰撞。本文采用L-N接触力模型和修正的Coulomb摩擦力模型,来建立含间隙旋转副的接触力模型。

1.2.1 间隙矢量模型

建立合理的间隙矢量模型,用来描述铰接处两元素相对位置的变化,如图2所示。

图2 间隙矢量模型Fig.2 Clearance vector model

(1)

当两元素发生碰撞时,碰撞深度为

δ=e-c

(2)

式中:e为两元素的偏心距;c为两元素的半径差。将δ作为判断轴套和轴销是否发生碰撞的标准,当δ<0时,两元素未接触,自由运动;当δ=0时,两元素开始接触或开始脱离;当δ>0时,两元素发生碰撞。

1.2.2 法向接触力模型

法向接触力模型表示运动副处元素间接触时的法向作用力。目前应用最广泛的接触力模型是由Lankarani和Nikravesh两位科学家在Hertz接触力数学模型基础之上提出来的L-N模型,该模型考虑了由材料阻尼引起的能量损失[15]。

基于L-N模型的法向接触力Fn表达式如下

(3)

接触刚度系数K的大小取决于接触表面的几何形状,对于两圆柱面的接触,K表达式为

(4)

(5)

式中:σi、σj为接触体的材料系数;Ri、Rj为接触体的接触半径;E为材料弹性模量;v为材料泊松比。

阻尼系数D的表达式为

(6)

将式(4)和式(6)代入式(3),即可得到法向接触力Fn表达式

(7)

1.2.3 切向摩擦力模型

目前Coulomb摩擦力模型是应用最广泛的摩擦力模型,适用于碰撞中的摩擦行为。然而当摩擦力由静摩擦向动摩擦过渡时,该模型与实际情况不符,本文采用修正的Coulomb摩擦力模型,其表达式如下[17-18]

(8)

(9)

式中:vt、vs和vd分别为相对滑动速度,静摩擦速度和动摩擦速度;μs为静摩擦因数;μd为动摩擦因数。

1.3 熵权法

熵权法就是依据各指标数据所包含的信息量大小来确定指标的权重。设影响机构运动非线性的因素的向量集合为{E1,E2,…,En},每个集合存在m个判定单元,那么关于机构运动非线性影响因素的判断矩阵为

(10)

式(10)中每一行表示同一个影响因素的不同判断单元,每一列代表不同影响因素的同一个指标。因为每个判断单元的含义并不完全相同,所以需要对原始数据进行标准化处理。

采用min-max标准化对数据进行归一化,使原始数据统一落入[0,1]区间内,目的是保证数据的可靠性,减少由于数据相差太大,导致数值较高的指标影响过大,从而削弱数据较小的指标的作用。

假设给定了k个指标X1,X2,…,Xk,其中Xi={x1,x2,…,xn}。假设对各指标数据标准化后的值为Y1,Y2,…,Yk,那么

(11)

根据标准化之后的数据Y1,Y2,…,Yk可以建立信息熵权的标准判断矩阵F。

根据信息论中信息熵的定义,一组数据的信息熵为

(12)

其中

(13)

如果pij=0,则定义

(14)

根据式(12)得到的各指标信息熵值E1,E2,…,Ek,可以得到各指标的权重。信息熵权的公式为

(15)

式中:k是信息熵权值的总数;Ei是信息熵。

2 考虑间隙和构件柔性的2-RR&2-PR并联机构运动特性仿真

为呈现不同条件下的仿真模拟,对2-RR&2-PR并联机构在考虑间隙及综合考虑间隙和构件柔性的情况下进行仿真分析。其中,在考虑间隙的条件下又分别对间隙大小及间隙个数对机构的影响进行分析。考虑到实际机构工作情况,设转速为240 r/min,同时为了提高仿真效率,将仿真模拟时间设为3 s,仿真步数设为3 000,本文所用到的求解器为GSTIFF求解器。

为了仿真时更加精确地计算出间隙处的接触力,根据1.2节中建立的接触力模型,采用Fortran语言编写程序,将此程序加载到ADAMS函数求解库中,用来求解间隙处两元素间作用力,具体流程如图3所示。将模型导入到ADAMS中,利用ADAMS的二次开发功能,通过ADAMS/Solver模块编译生成的动态链接库文件(*dll),然后利用ADAMS/View模块调用自定义函数,即生成的动态链接库文件,就可将此自定义函数应用到模型中,再进行模型仿真,其中接触力模型参数取值如表2所示。

图3 自编子程序的实现Fig.3 Implementation of self-programmed subroutines

表2 接触力模型参数Tab.2 Contact force model parameter

此程序代码的核心内容是将间隙处两元素的运动学特征和旋转副自身的几何特征综合在一起,包含了间隙处两元素在运动过程中无接触、点接触、线接触、面接触四种模式的描述。在仿真过程中通过该程序中的SYSARY子函数从模型中提取系统的状态参数,完成接触模式实时判别,从而依据不同接触模式下的解析表达,计算出接触力。

2.1 仿真数值计算

数值计算结果影响了仿真数据的准确性。为了确保仿真结果的准确性,有必要分析数值分析的误差,以证明分析结果是收敛的,并且当时间和步长变化时,计算结果不会改变,因此增加了数据分析过程。

图4显示了t=0.9 s时轴销中心点在X方向上的位移。图4(a)表明,在相同积分阶数条件下,结果在10次迭代后趋于稳定,计算效率最高。值得注意的是,当迭代次数小于3时,仿真无法满足收敛条件,导致仿真失败。图4(b)表明,在相同的迭代次数条件下,结果在积分阶数达到2阶后趋于稳定。为了确保后续数据的准确性和计算效率,6阶、10次迭代组合是最佳选择。

(a) 不同迭代次数

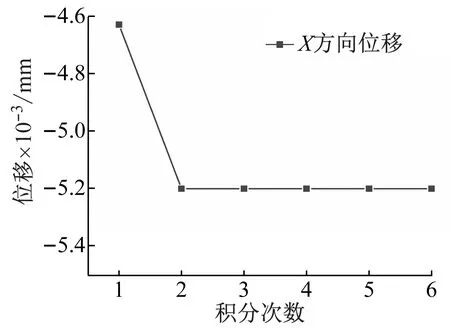
(b) 不同积分阶数图4 轴销中心点在X方向上的位移Fig.4 Displacement of shaft pin center point in X direction

2.2 间隙对机构的影响

2.2.1 间隙大小对机构的影响

将间隙处大小设置成0.04 mm、0.06 mm、0.08 mm和0.10 mm,利用MATLAB将仿真加速度数据进行短时傅里叶变换处理,绘制成不同间隙大小下加速度幅值的变化曲线如图5所示。

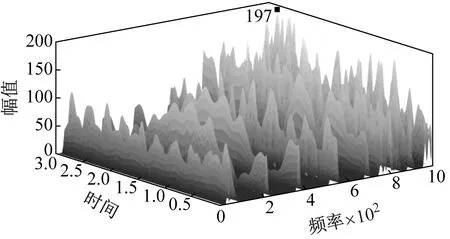
(a) c=0.04 mm

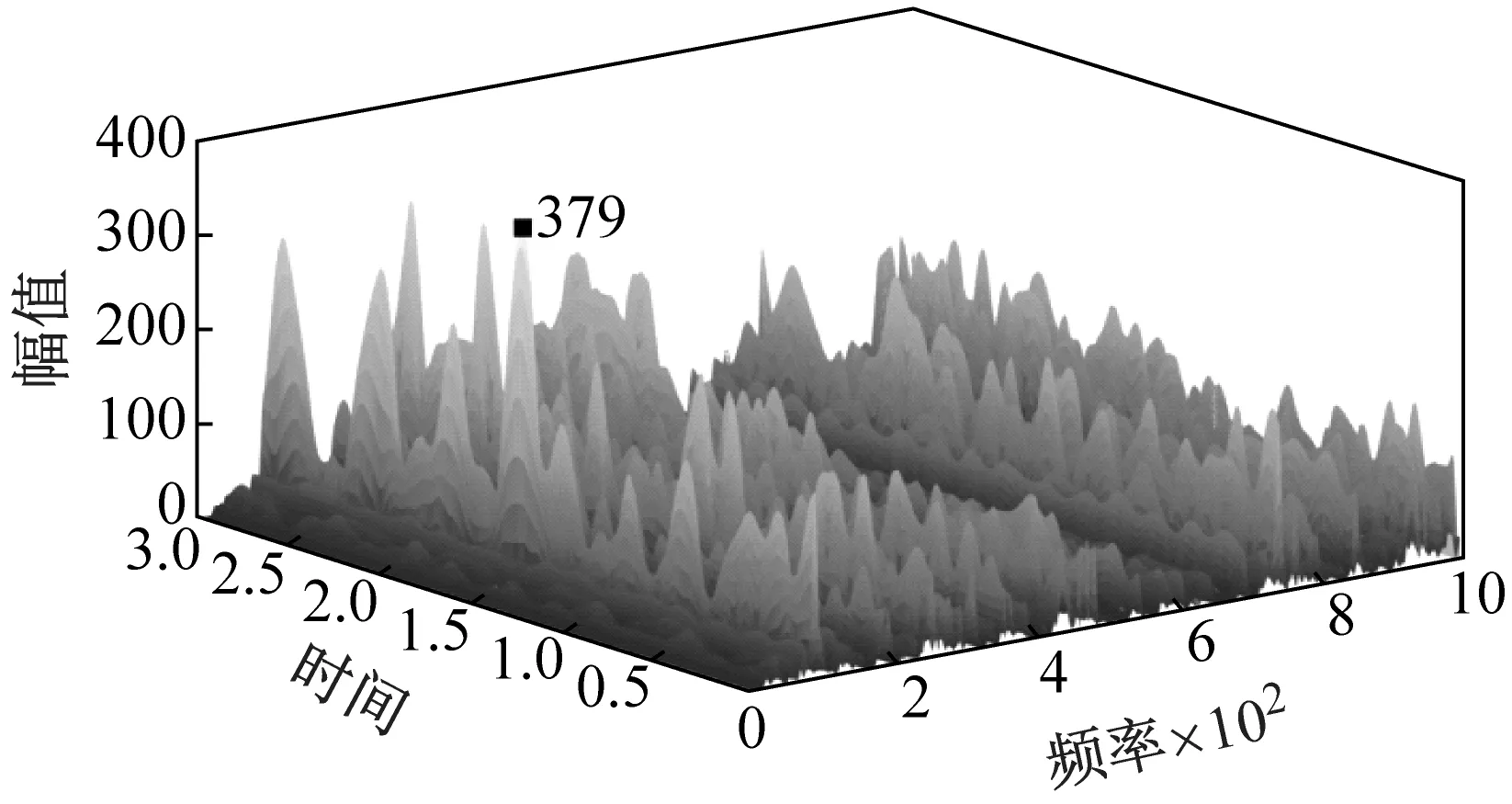
(b) c=0.06 mm

(d) c=0.10 mm图5 间隙大小对机构动平台加速度的影响Fig.5 Influence of clearance size on the acceleration of the mechanism moving platform

从图5可以看出,引入间隙后,机构动平台的加速度有剧烈的波动,表现为明显的非线性现象。随着间隙值从0.04 mm增大到0.06 mm,含间隙机构加速度的最大幅值从197增加到了379,间隙值从0.06 mm增加到0.10 mm时,机构加速度的最大幅值又降低到了114。由此可以看出,在一定范围内随着间隙值的增大,间隙对加速度的影响也有所增大。但当间隙增加到一定值后,随着间隙值的增大,间隙对加速度的影响会趋于减小。机构在运动时,间隙使得转动副处产生接触碰撞力,并使这些接触碰撞力产生波动,从而导致了加速度的变化。

2.2.2 间隙个数对机构的影响

以含有两个关节间隙的并联机构为研究对象,研究间隙个数对机构的影响。通过仿真得到间隙个数对机构动平台加速度的影响如图6所示,其中两个关节间隙的尺寸都为0.1 mm。当机构中含有一个间隙时,机构加速度的幅值最大如图5(d)所示为114。当机构中含有两个间隙时,机构加速度的幅值最大为183。

图6 间隙个数对机构动平台加速度的影响Fig.6 Influence of the number of clearances on the acceleration of the mechanism moving platform

通过图6可以看出,不同间隙个数的机构,其加速度产生波动的规律并不相同,且相对于机构只含一个间隙的情况下,当机构含有两个间隙时,动平台加速度的最大幅值有所增大,说明双间隙情况下机构动平台明显波动得更加剧烈。产生这种现象的原因是间隙与间隙之间的相互耦合作用,当存在多个间隙时,间隙之间相互影响,使得加速度明显增大,意味着产生了更大的接触碰撞力,机构更难趋于稳定。

2.3 综合考虑间隙和构件柔性对机构的影响

刚体在受力后不会产生任何变形,而实际中任何物体在受到力的作用后,都会产生变形,为了更精确地揭示机构运动状态,需要考虑构件的柔性。

将图1中2-RR&2-PR并联机构的A3A5、A4A6两构件柔性化处理,通过ANSYS和ADAMS软件联合生成构件柔性化模型,将构件三维模型导入到ANSYS中,在ANSYS中创建单元和材料,设置材料密度属性的参数选择如表3所示。

表3 材料参数选择Tab.3 Material parameter selection

通过划分网格,在构件两端的孔处设置刚性连接区域,确定关键点,建立刚性连接区域,从而生成模态中性文件(MNF文件)。MNF文件包含了ADAMS中柔性体的所有信息,在ADAMS中直接导入MNF文件,从而生成机构的刚柔耦合模型。

在2.2节中间隙尺寸分别为0.04 mm、0.06 mm、0.08 mm和0.10 mm,针对不同间隙尺寸下的模型,分别导入构件的MNF文件,将构件柔性化,建立含间隙和构件柔性耦合机构的仿真模型。

通过仿真得到综合考虑间隙和构件柔性情况下对机构动平台加速度的影响图。为了更好地揭示给机构带来的影响,选取间隙尺寸为0.06 mm情况下机构动平台加速度的影响图如图7所示。

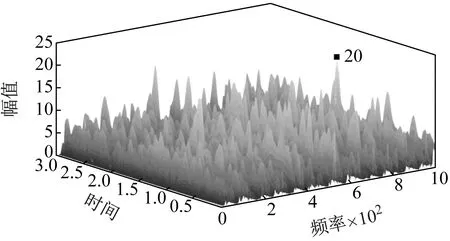
图7 综合考虑间隙和构件柔性对机构动平台加速度的影响Fig.7 Comprehensive consideration of the influence of clearance and component flexibility on the acceleration of the mechanism moving platform

由图5(b)可以得到只考虑间隙时,动平台加速度的最大幅值为379,而综合考虑间隙和构件柔性时,由图7可以得到,动平台加速度的最大幅值为20,相比之下大幅度减小。

图8为仿真得到的综合考虑间隙和构件柔性对间隙铰链处接触力的影响图,其中间隙尺寸为0.06 mm,从图8可以看出,只考虑间隙时最大接触力约为50 N,而综合考虑间隙和构件柔性的情况下接触力有所减小,约为17 N,其中各个时间点所显示的接触力没有明显的规律,代表机构运动时间隙铰链处具有非线性。而接触力有所减小是因为当在关节间隙处的两元素发生碰撞时,柔性构件可以起到明显的缓冲作用,从而对接触力和加速度偏差进行补偿,大幅度缓和了间隙处两元素的碰撞。同时可以看出间隙和构件柔性对机构运动及性能的影响不能相互抵消,所以对机构进行分析时有必要综合考虑间隙和构件柔性。

图8 综合考虑间隙和构件柔性对间隙铰链处接触力的影响Fig.8 Comprehensive consideration of the influence of clearance and component flexibility on the contact force of the mechanism moving platform

3 2-RR&2-PR并联机构定量分析

现有的评估机构非线性行为的定量分析方法主要是Lyapunov指数法,该方法通过Lyapunov指数的正负来判断系统是否具有混沌特性,但没有具体分析不同因素对机构非线性的影响程度,需要一种新的定量分析方法,在此基础上去衡量不同因素对机构非线性的影响程度。本文提出一种基于熵权法的非线性定量分析新方法,通过计算各影响因素的相对比例,根据熵权法的定义计算出各影响因素下的熵权值,以此评估不同条件下间隙和构件柔性对机构非线性的影响程度。

3.1 Lyapunov指数法定量分析

Lyapunov指数法中正指数表示系统具有混沌特性,其中只需求解最大Lyapunov指数即可。选取机构动平台加速度为计算对象进行混沌分析,在MATLAB中计算得到

(16)

式中:tw为时间窗口;tau为时间延迟;m为嵌入维数;P为平均周期。

将所得数据代入最大Lyapunov指数程序,计算结果如图9(a)所示。选择虚线矩形中所示的线性区域,用最小二乘法在该区域拟合直线。拟合直线的斜率为最大Lyapunov指数,如图9(b)所示。显然所得最大Lyapunov指数大于零,验证了该系统具有混沌特性。

(a) 最初结果

(b) 线性拟合结果图9 最大Lyapunov指数的估计Fig.9 Estimation of the maximum Lyapunov exponent

3.2 基于熵权法的考虑间隙的机构定量分析

将前文2.2节中的仿真参数设为组别1～5,如表4所示。图10为不同间隙条件下机构动平台在X、Y、Z方向上加速度的仿真数据图,利用MATLAB编写熵权法程序,将仿真数据代入程序中,计算在不同间隙大小及间隙个数情况下的熵权值。

表4 机构仿真参数Tab.4 Mechanism simulation parameters

(a) c=0.04 mm

(b) c=0.06 mm

(d) c=0.10 mm

(e) c=0.10 mm图10 不同间隙条件下X、Y、Z方向加速度变化图Fig.10 The change of acceleration in X, Y and Z directions with different clearance conditions

如表5所示,为计算得到的不同间隙条件下机构动平台X、Y、Z方向加速度熵权值。绘制不同间隙大小下(组别1～4)的熵权值变化图如图11所示,其中图11(a)为折线图,为了更直观呈现间隙对加速度影响程度,绘制成雷达图如图11(b)所示。绘制不同间隙个数下(组别4～5)的熵权值变化雷达图如图12所示。

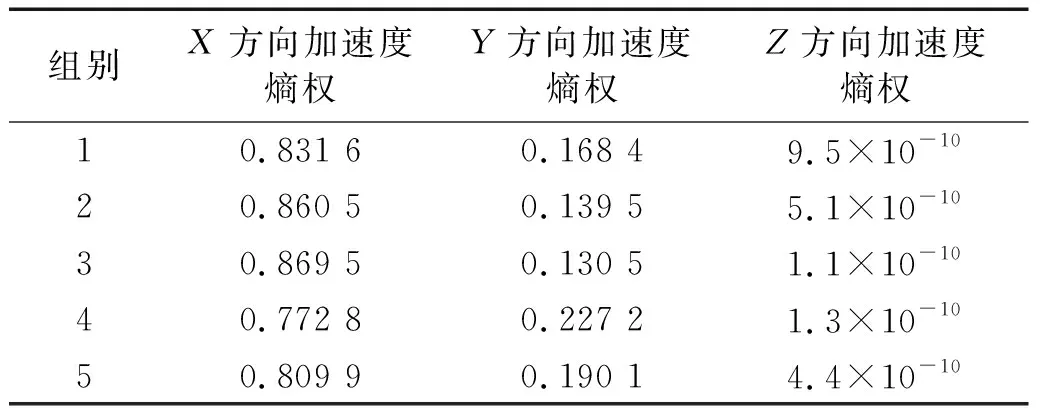
表5 不同间隙条件下的加速度熵权Tab.5 Entropy weight of acceleration with different conditions

(a) 熵权折线图

(b) 熵权雷达图图11 不同间隙大小下的熵权变化图Fig.11 Entropy weight change map for different clearance sizes

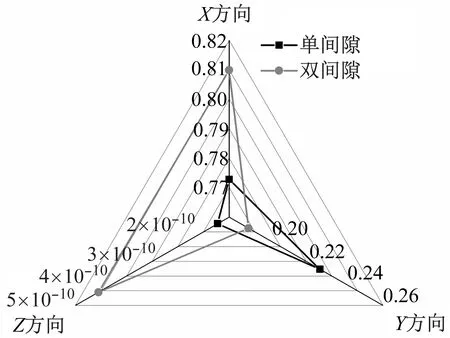
图12 不同间隙个数下的熵权值变化雷达图Fig.12 Radar plot of entropy weight change with different number of clearances

图11(a)显示了加速度熵权的变化趋势,图11(b)显示了不同方向上加速度影响程度的变化。如图11(a)所示,随着间隙尺寸的变大,加速度在Z方向上的熵权几乎不发生变化,一直趋于0,在X方向和Y方向上的熵权都会发生变化,其中加速度X方向上的熵权值远大于Y方向的熵权值,代表X方向的加速度对间隙尺寸的变化比较敏感,对加速度影响权重最高。同时从第1组到第4组可以看出随着间隙值的增大,X方向加速度熵权值先增大后减小,代表间隙对机构X方向加速度的影响先增大后减小,相应的Y方向加速度熵权值先减小后增大,代表间隙对机构Y方向加速度的影响先减小后增大。

图12为不同间隙个数下的熵权值变化雷达图,显示了不同间隙个数下加速度影响程度的变化。从图12可以得出随着间隙个数的增加,X方向加速度熵权值增大,对加速度影响权重提高,代表对机构X方向加速度的影响逐渐增大,约为Y方向上的4倍。

3.3 基于熵权法的考虑间隙和构件柔性的机构定量分析

将前文2.3节中的仿真参数设为组别1和2,如表6所示,其中第一组的仿真参数与3.2节中的第二组一致,作为对照组。图13为考虑间隙和构件柔性条件下机构动平台在X、Y、Z方向上加速度的仿真数据图,采用相同的方法计算在含间隙机构中引入构件柔性情况下的熵权值。

表6 机构仿真参数Tab.6 Mechanism simulation parameters

图13 考虑间隙和构件柔性条件下X、Y、Z方向加速度变化图Fig.13 The change of acceleration in X, Y and Z directions with considering clearance and component flexibility

如表7所示,为在含间隙机构中引入构件柔性情况下计算所得的熵权值,其中第一组为对照组,熵权值与3.2节中的第二组一致。将计算的结果绘制成雷达图如图14所示。

表7 考虑间隙和构件柔性条件下的加速度熵权Tab.7 Entropy weight of acceleration under consideration of clearance and component flexibility

图14 考虑间隙和构件柔性下的熵权值变化雷达图Fig.14 Radar plot of entropy weight change under consideration of clearance and component flexibility

图14显示了在含间隙机构中引入构件柔性情况下加速度影响程度的变化。从图14可以看出,在考虑构件柔性的情况下X方向和Y方向上的熵权都会发生变化,其中加速度X方向上的熵权值远大于Y方向的熵权值,代表X方向的加速度在考虑构件柔性时比较敏感,对加速度影响权重最高,且X方向加速度熵权值有所增大,代表对机构X方向加速度的影响程度增大,Y方向加速度熵权值有所减小,代表对机构Y方向加速度的影响程度减小。同时综合表5和表7的数据可以发现,在任何条件下,动平台X方向加速度熵权值最大,所占权重最高,而Z方向加速度熵权几乎不发生变化,这也体现出本文所做的各组仿真之间的关联性。