锥度和不对中误差对止推箔片轴承承载特性的影响

连军伟,张茂森,金志磊,贺雷

(1.中国航天科技集团有限公司 低温液体推进技术实验室,北京 100076;2.北京航天动力研究所,北京 100076)

1 概述

人类探测太空的能力主要受空间推进技术的限制,针对高速度增量的航天任务,传统化学推进技术的比冲较低,太阳能电池阵—蓄电池技术严重依赖太阳光照,深空生存能力较差[1]。空间核电源系统具有能量密度大,容易实现大功率(数千瓦至数兆瓦)供电,机动性和隐蔽性好,不依赖太阳光照等优势,是深空探测不可替代的空间电源[1]。

动态转换的放射性同位素发电系统在空间核电源系统中转换效率最高,其中研究较多且已应用的是闭式布雷顿循环的动力转换系统(图1),旋转单元是该系统的核心组件,其结构和性能直接影响系统的优劣。止推箔片轴承作为一种柔性自适应动压轴承,在旋转单元中承受轴向载荷,与滚动轴承相比,省略了复杂的冷却润滑系统,使系统更加清洁和高效。

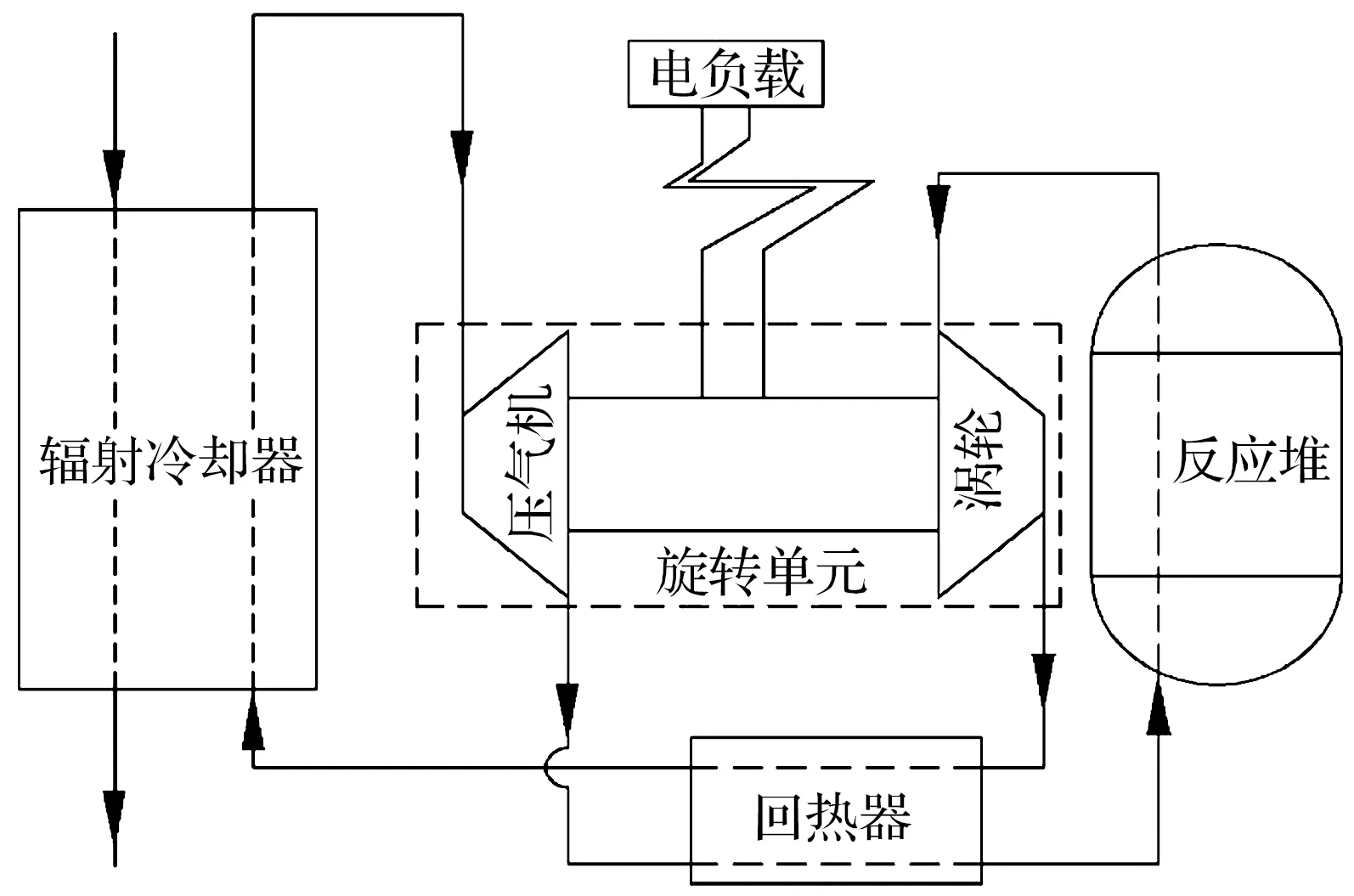
(a) 闭式布雷顿循环系统原理

1854年,法国科学家提出将气体作为润滑剂的可能,1886年法国科学家雷诺推导出润滑膜内压力分布的雷诺方程[2],对流体润滑的认识上升到理论高度。止推箔片轴承作为阶梯型动压轴承的衍生结构轴承,具有波箔刚度非线性的特点,其理论研究晚于径向箔片轴承且相关研究较少。1983年,文献[3]对止推箔片轴承的静态特性进行了详细的计算分析,计算模型考虑了波箔刚度的非线性分布,第1次使用柔度系数α分析箔片轴承静特性,该方法一直沿用至今。2000年,文献[4]采用有限差分法与有限元相结合的方法,将可压缩流体的雷诺方程求解与弹性变形耦合起来进行止推箔片轴承分析。2017年,文献[5]采用非等温雷诺方程评估了转子静态和动态角度不对中对止推箔片轴承性能的影响,并深入分析了轴承的承载力、摩擦功、气膜刚度和阻尼系数的变化情况。

20世纪80年代,文献[6]应用圆柱薄壳线性理论推导出波箔变形方程,这是国内最早关于箔片轴承中波箔刚度的计算模型。文献[7]采用有限单元法对平箔式止推箔片轴承进行求解,并分析了箔片轴承静态特性的影响因素。文献[8]对止推箔片轴承进行了启停试验,分析了箔片材料和表面涂层对轴承启停磨损的影响。文献[9]采用有限差分法得出,推力盘倾斜状态下轴承的轴向承载力和黏性摩擦力矩均随倾角的增大而增大,且倾角越大静态特性越大。文献[10]基于牛顿迭代法建立偏角不对中时止推箔片轴承的润滑模型,与线性替换法的比较说明牛顿迭代法具有同样的适用性。文献[11]基于CFX的有限元计算与MATLAB的有限差分求解动压气体轴承气膜压力,二者计算结果一致,随着偏心率的增加CFX有限元的计算结果比有限差分法计算的略小。文献[12]采用ANSYS和CFX软件计算了超临界二氧化碳止推箔片轴承动态特性,得出动态刚度和阻尼大小主要取决于气膜厚度和箔片结构,且随气膜厚度的增大而减小。随着更多类型箔片轴承的研究,箔片轴承的性能逐渐被熟知,但仍缺乏精准的理论分析模型和实用的设计规范[13]。

综上可知,目前在止推箔片轴承的误差研究方面,主要着重于轴承不对中误差对其静态性能的影响,而锥度误差对轴承承载特性的影响以及不对中误差下轴承动态特性变化的研究较少。在生产和装配过程中,锥度和不对中误差均难以避免,不对中误差主要有平行不对中、角不对中和综合不对中。由于旋转单元转子系统的径向设计间隙约束及推力盘径向尺寸大于止推轴承高度,分析过程不考虑平行不对中的影响,本文所提及的不对中特指角不对中或主轴倾斜。本文在柱坐标系下建立止推箔片轴承的雷诺方程,并采用牛顿迭代法和有限差分法对雷诺方程和气膜厚度方程进行耦合求解,分析生产和装配过程引起的径向锥度误差和不对中误差对止推箔片轴承承载特性的影响。

2 理论分析

止推箔片轴承主要由顶箔、波箔和底板组成。波箔和顶箔组成多个扇形瓦,每个瓦的度数和倾斜面占比相同。止推箔片轴承结构和箔片参数示意图如图2所示,β为扇形瓦的瓦角,βp为扇形瓦节线位置角,σh为扇形瓦倾斜面高度,ω为推力盘角速度,h2为设计间隙。

(a) 止推箔片轴承 (b) 箔片参数

2.1 压力控制雷诺方程推导

推导等温条件下的雷诺方程时进行如下假设:1)忽略气体惯性力;2)润滑气体介质视为牛顿流体,符合牛顿黏性定律;3)气膜间隙内为层流;4)忽略气膜法向流动;5)润滑介质视为理想气体。

经推导得到柱坐标下润滑介质为理想气体的雷诺方程,即

(1)

式中:r为径向坐标;h为气膜厚度;P为气膜压力;θ为周向坐标;μ为气体动力黏度。

(2)

式中:Pa为环境压力;R2为轴承外半径;Λ为轴承数。

2.2 气膜厚度方程

每个扇形瓦的气膜由倾斜面气膜和水平面气膜组成,根据图2的结构参数得到单个扇形瓦的气膜厚度方程,即

h=h2+h(θ)+w(r,θ) ,

(3)

式中:w(r,θ)为箔片变形后构建的变形区域气膜厚度;h(θ)为扇形瓦倾斜面气膜厚度。

定义b为斜面占比,b=βP/β,气膜厚度的表达式为

(4)

在工程应用过程中存在加工误差,推力盘不可避免地产生一定的径向锥度βz,将直接影响气膜厚度分布。锥度为负数时表示推力盘出现内锥状态,为正数时出现外锥状态, 按内锥度和外锥度这2种形式构建径向锥度模型(图3),Ri为锥度半径,R1为轴承内半径,Δh为锥度引起的气膜厚度变化。锥度βz的定义为

(a) 内锥度

(5)

建立考虑推力盘径向锥度的气膜厚度方程,即

h0=h2+h(θ)+w(r,θ)+Δh。

(6)

尽管设计及生产过程要严格控制形位公差,但在装配过程仍会存在不对中现象[14-15],而不对中误差会导致止推箔片轴承气膜间隙发生变化,从而引起轴承承载特性的改变。如图4所示,建立不对中模型和空间坐标系。

(a) 坐标系及扇形瓦标记

假设转子与止推箔片轴承的夹角(不对中角度)为φ,在空间坐标下可分解为绕x轴的θx和绕y轴的θy。考虑转子不对中的气膜厚度方程为

h1=h2+h(θ)+w(r,θ)-rcosθtanφ。

(7)

2.3 波箔刚度等效模型

波箔单位面积刚度Kb的表达式为

(8)

式中:Eb为波箔的弹性模量;t为波箔厚度;l为半波箔长度;s为波箔单位长度;ν为波箔的泊松比。

2.4 网格划分及边界条件

图5 单个扇形瓦的网格划分

2.5 流固耦合计算流程

采用有限差分法求解(2)式得到气膜压力,通过迭代由(9)式判断是否收敛。基于MATLAB平台按图6程序逻辑进行编译计算。

图6 止推箔片轴承计算程序逻辑图

(9)

3 计算与分析

3.1 程序验证

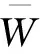
(10)

式中:W为承载力。

本文程序计算与文献[3]的对比结果如图7所示,最大误差为2.53%,两者吻合度较好,说明本文止推箔片轴承数学模型的准确性较高。

图7 本文程序与文献[3]计算结果对比

3.2 锥度误差的影响

空间核电动力转换系统的止推箔片轴承结构参数及其他参数见表1。

表1 止推箔片轴承结构参数及其他参数

锥度一定时,各扇形瓦气膜厚度和气膜压力在同一半径和周向角度上相同,为提高计算精度并减少计算时间, 选取单个扇形瓦进行分析。 在额定设计间隙下,内锥(Ri=R1)和外锥(Ri=R2)状态下量纲一的气膜压力和气膜厚度分布如图8和图9所示:当内锥度为-4×10-4时,最大气膜压力增大18.4%,对应轴向承载力提高47.8%;当外锥度为4×10-4时,最大气膜压力减小12.7%,对应轴向承载力降低33.8%。以图9b中气膜厚度A和B位置为基准,内锥度为-4×10-4时B区域的气膜厚度减小至10.6 μm,外锥度为4×10-4时A区域的气膜厚度增大至29.4 μm。综上可知:内锥度减小了平均气膜厚度,提高了承载力;外锥度增大了平均气膜厚度,降低了承载力。

(a) -4×10-4

(a) -4×10-4

设计间隙不变时轴向承载力和摩擦功随锥度的变化以及轴向载荷恒定(200 N)时最小气膜厚度和量纲一的最大气膜压力随锥度的变化如图10所示:设计间隙不变时,轴向承载力和摩擦功随着锥度的增加逐渐减小,由于锥度的增加增大了平均气膜厚度,削弱了动压效应进而减小了轴向承载力和摩擦功。在轴向载荷恒定时,随着锥度绝对值的增加,最小气膜厚度逐渐减小, 最小气膜厚度达到0.67 μm,若继续减小至零时程序计算很难收敛,由于模型未考虑表面粗糙度, 工程应用时可认为此时轴承已处于临界碰磨状态。说明恒定载荷工况时只有允许一定范围的锥度误差才能保证轴承正常运行。最大气膜压力与最小气膜厚度正好相反,说明轴向载荷恒定时只要锥度绝对值增加就会增大最大气膜压力。此外,内锥度和外锥度引起的最大气膜压力和最小气膜厚度均关于锥度βz=0对称。

图10 止推箔片轴承静态参数随锥度的变化

3.3 不对中的影响

为简化分析模型,掌握不对中对轴承性能的影响,只选取绕某一轴倾斜产生的不对中进行分析。对中和不对中时止推箔片轴承的气膜压力、气膜厚度和箔片变形如图11所示:由于不对中的产生,轴承各瓦的气膜压力和气膜厚度分布不均匀,箔片产生的变形量也不同;2#瓦最大气膜压力(2.458)最大,高于对中状态下各瓦的最大气膜压力(1.805),5#瓦的最大气膜压力最小(1.494);由于气膜压力作用,最大变形量为(1.205 μm)同样出现在2#瓦上,是5#瓦最大变形量(0.412 μm)的2.925倍;由于箔片变形构建了新的气膜承载区域,气膜压力越高时箔片变形量越大,体现了止推箔片轴承较好的自适应性。

(a) 不对中状态(θx=0.01°)

止推箔片轴承和各瓦的承载力和摩擦功随不对中角度的变化如图12所示:轴承的承载力和摩擦功随着不对中角度的增大而增加,但各瓦不同;当推力盘按图4坐标系倾斜时,x轴上方的3个扇形瓦平均气膜厚度减小,动压效应增强,气膜压力升高,承载力和摩擦功随不对中角度的增大而增加,2#瓦平均气膜厚度最小,其承载力最大且增速最快,1#瓦次之,3#瓦增速最慢,x轴下方3个扇形瓦则相反;不对中造成各瓦的承载力和摩擦发热严重不均衡,不对中角度越大时各瓦的差异越大。

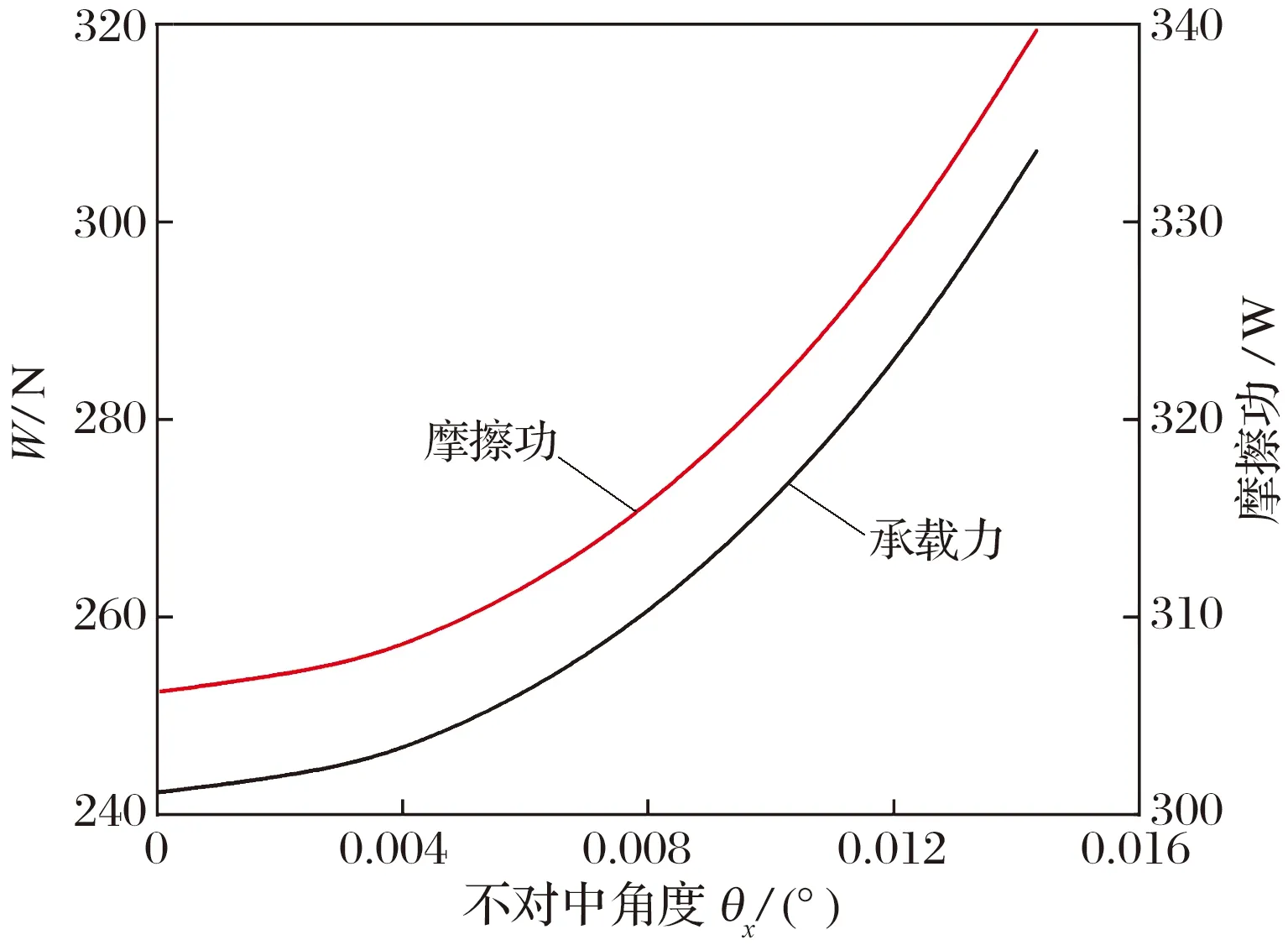
(a) 轴承的承载力和摩擦功

由于不对中的存在,止推箔片轴承不仅产生沿轴向的位移刚度,还存在沿径向的弯曲刚度。图4中轴承产生绕x轴的弯矩Mx; 由于1#, 6#瓦与3#, 4#瓦承载力的差异及2#, 5#瓦关于y轴不对称,产生绕y轴的弯矩My,则轴承在3个自由度上有9个刚度系数和9个阻尼系数,组成的刚度系数矩阵K和阻尼系数矩阵C分别为

(11)

(12)

刚度系数和阻尼系数随不对中角度的变化如图13所示:当绕x轴倾斜时,轴向主刚度系数和主阻尼系数比轴向交叉项的大,随着不对中角度的增大,轴向主刚度系数和主阻尼系数变化较明显;在绕x轴方向,交叉项Kzθx和Czθx随不对中角度的变化较明显,且幅值远高于其他项,主要原因为不对中角度增加,承载力快速增大,造成承载力在该方向的交叉弯曲刚度系数和阻尼系数增大;在绕y轴方向,交叉项Czθy随不对中角度变化较明显且为负数,刚度系数主项Kθyθy的变化最大,当θx为0.016°时,主项Kθyθy增幅为28.5%,交叉项Kzθy增幅为22.1%,说明在绕y轴方向,随着不对中角度的增加,由弯矩My和承载力引起的刚度变化占主导。上述现象说明不对中角度对止推箔片轴承的刚度系数和阻尼系数的影响较大,而刚度系数和阻尼系数直接影响转子系统的稳定性。

4 结论

基于牛顿迭代法和有限差分法,耦合求解考虑径向锥度和不对中误差影响的气膜厚度方程及压力控制的雷诺方程,对闭式布雷顿循环系统的止推箔片轴承进行承载特性影响因素分析,得到如下结论:

1)在设计间隙一定的情况下,内锥度会减小平均气膜厚度,进而增大轴承承载力,当内锥度为-4×10-4时,承载力增大47.8%;外锥度会增大平均气膜厚度,进而降低承载力,当外锥度为4×10-4时,承载力降幅达到33.8%。在轴向载荷为200 N时,最小气膜厚度随着锥度绝对值的增加而减小,当锥度大于2.25×10-3时,轴承进入临界碰磨状态。生产过程应严格控制推力盘的锥度,避免因加工误差过大而造成轴承失效。

2)不对中会改变轴承各瓦的气膜压力和气膜厚度分布,当不对中角度θx=0.01°时,最大气膜压力增加36.2%。不对中角度造成各瓦的承载力严重不均衡,对轴承刚度系数和阻尼系数的影响较明显,直接影响转子系统的稳定性。随着不对中角度的增大,轴承的摩擦功呈指数形式增加,导致轴承的发热量急速上升,装配过程应尽可能将不对中误差降到最低。