内、外圈沟道表面形貌对双半内圈角接触球轴承游隙的影响

2023-10-17孙奇杨晓峰孙喆高阳

轴承 2023年10期

孙奇,杨晓峰,孙喆,高阳

(1.中国航发哈尔滨轴承有限公司,哈尔滨 150025;2.空军驻哈尔滨地区第一军事代表室,哈尔滨 150025)

传统的滚动轴承轴向游隙通过测量轴承径向游隙后换算得到,随着检测技术的发展,可以采用专用仪器精确测量轴承轴向游隙,也可以通过改进的测量方法测量轴承轴向游隙[1-4]。双半内圈角接触球轴承的轴向游隙会影响轴承的载荷分布、疲劳寿命和力矩刚性,简单的经验公式计算已不能满足轴向游隙精确控制的要求[5]。文献[6]提出五点不变原理和沟心距不变原理,并应用于单列和双列向心球轴承径向游隙、轴向游隙和初始接触角的计算; 文献[7]计算了双半内圈球轴承在正常接触、临界接触和非正常接触条件下的接触角,并计算了保证轴承在正常条件下工作的垫片厚度,进而对轴承游隙进行计算;文献[8]推导了三点、四点接触球轴承游隙和接触角的通用计算公式;文献[9]推导了三点接触球轴承双半内圈结构参数不同时径向游隙、轴向游隙的计算方法;文献[10]考虑球接触变形的非线性,建立三点接触球轴承有限元仿真模型,通过仿真得到轴承游隙,克服了理论公式难以进行非线性计算的缺点。

上述轴承游隙计算方法均未考虑内、外圈沟道真实形貌对轴承游隙的影响。因此,本文考虑内、外圈沟道真实接触形貌,建立双半内圈角接触球轴承有限元模型,通过对真实形貌进行傅里叶分解,分析1阶形貌和2阶形貌对轴承径向游隙和轴向游隙的影响。

1 考虑套圈真实形貌的轴承游隙计算

双半内圈角接触球轴承由1个整体的外圈、2个内圈、球、保持架组成,其截面参数如图1所示,图中:di,De分别为内、外圈沟底直径;Dw为钢球直径;Ri,Re分别为内、外圈沟道半径;hi为内圈沟心距;αs为垫片角;Gr为径向游隙;Ga为轴向游隙;α0为初始接触角。

套圈的真实形貌会影响内、外圈沟底直径,不同球位置的沟道形貌不同,内、外圈沟底直径也不同,导致不同球位置的径向游隙和轴向游隙不同。轴承的径向(轴向)游隙是当轴承无外载荷作用时,一个套圈相对另一套圈从一个径向(轴向)极限位置移向相反极限位置的径向(轴向)距离,此极限值就是轴承径向(轴向)游隙的最大值。

轴承径向游隙、轴向游隙计算公式分别为

(1)

Ga=-hi+2[

(Ri+Re-Dw)2-

(2)

内、外圈沟道表面形貌的表达采用傅里叶分解,根据傅里叶分析的定义将形貌函数分解为一系列正弦函数相加的形式,即

(3)

则考虑套圈沟道真实形貌时轴承的径向游隙、轴向游隙分别为

Gr=De-di+2Kea-2Kia-Dw-

(4)

Ga=-hi+2[

(Ri+Re-Dw)2-

(5)

式中:Ai为第i阶形貌的振幅;n为波峰和波谷的数量,也是形貌的阶数;θ为球方位角,θ∈[0,360°);φi为第i阶形貌的相位;Kea,Kia分别为外、内圈的径向跳动。

2 有限元模型

由(4),(5)式可知影响双半内圈角接触球轴承游隙的主要参数有:内圈沟心距hi、内圈沟道半径Ri、外圈沟道半径Re、内圈沟底直径di、外圈沟底直径De和钢球直径Dw。在有限元建模时需考虑这6个参数的影响。

为提高仿真精度和仿真效率,对内、外圈沟道和球的接触区域进行网格加密,如图2所示,采用薄层切割方法,在内、外圈沟道和球表面切出一个薄层,薄层和基体分别用2种网格密度进行绘制,MPC绑定连接对接触面与基体之间力的传递影响较小,用MPC绑定的方法将薄层和基体绑定。球与内、外圈沟道采用摩擦接触,摩擦因数设为0.1。有限元模型接触条件如图3所示。

图2 有限元模型网格划分

图3 有限元模型接触条件

为减少网格数量,本文轴承模型无保持架,为模拟保持架的作用,保证球之间的相对位置,采用命令流中CERIG的钢化节点的方法,选中全部球的中心,限制其绕x方向的旋转。为建立真实的内、外圈接触面,对真实接触形貌进行傅里叶分解,取前几阶的形貌参数输入模型并采用节点平移的方法构建形貌。

计算径向游隙时,对外圈施加固定约束,对内圈施加沿y轴负方向的径向力100 N,同时限制内圈在非施力方向的移动,再对轴承内圈施加反方向(沿y轴正方向)的径向力100 N,2次位移之和即为轴承径向游隙;计算轴向游隙时,对外圈施加固定约束,对内圈施加沿x轴正方向的轴向力100 N,同时限制内圈在非施力方向的移动,再对内圈施加反方向(沿x轴负方向)的轴向力100 N,2次位移之和即为轴承轴向游隙。

3 不同阶数的形貌对轴承游隙的影响

以某型号双半内圈角接触球轴承为例,其主要仿真参数见表1。

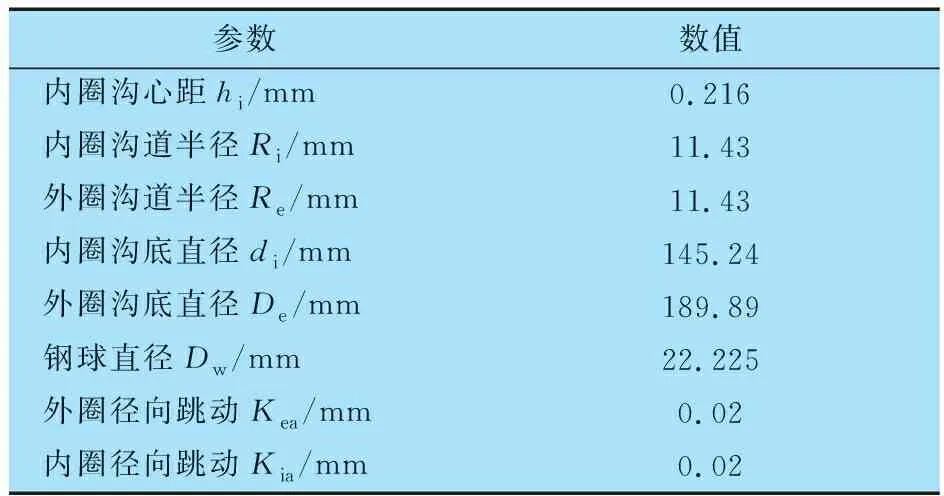
表1 双半内圈角接触球轴承主要仿真参数

通过(1),(2)式可得未考虑套圈沟道真实形貌时轴承的径向游隙和轴向游隙分别为0.163,0.470 mm。

对未考虑内、外圈沟道真实形貌(具有理想光滑表面)的轴承模型进行仿真,结果见表2,仿真和理论计算的径向游隙、轴向游隙接近,说明了有限元模型的正确性,误差主要来源于沟道和球的弹性变形。

表2 双半内圈角接触球轴承游隙仿真结果

在测量轴承径向游隙和轴向游隙的过程中,需分别对轴承施加径向力和轴向力,轴承受力的变形云图如图4所示。

(a) 受径向力时

在1阶形貌中,根据(3)式可得内、外圈沟道表面形貌的方程为

(6)

(7)

仿真结果见表2:在径向力方向(y轴负方向)的一侧,内、外圈的间隙增大,此方向的径向游隙比理想值大,但在径向力反方向(y轴正方向)的一侧,内、外圈的间隙减小,此方向的径向游隙比理想值小,因此总的径向游隙在1阶形貌中是不变的。由于轴承整体的轴向游隙取决于所有球中最小的轴向游隙,因此与理想形貌相比,轴向游隙要小很多。

在2阶形貌中,根据(3)式可得内、外圈沟道表面形貌的方程为

(8)

(9)

仿真结果见表2:2阶形貌不同于1阶形貌,内、外圈沟道的轨迹是一个椭圆,在径向力方向及其反方向,径向游隙比理想形貌要大,因此总的径向游隙比理想值大。但轴向游隙仍取决于所有球中最小的轴向游隙,与1阶形貌相比,轴向游隙无变化。

不同内、外圈沟道表面形貌下轴向游隙随轴向力的变化如图5所示:在相同轴向力下,1阶、2阶形貌的轴向游隙相差不大,理想形貌的轴向游隙大于1阶、2阶形貌。不同内、外圈沟道表面形貌下径向游隙随径向力的变化如图6所示:在相同径向力下,理想形貌、1阶形貌的径向游隙相差不大,2阶形貌的径向游隙大于理想形貌、1阶形貌。