轴承套圈周向裂纹漏磁信号一致性提升方法

彭广,杨芸,邱少雄,闵洲

(东华大学 机械工程学院,上海 201620)

轴承是现代工业机械设备至关重要的基础部件,广泛应用于各个领域,其质量和可靠性直接与机械装备的运行安全息息相关[1]。据统计,约90%的轴承套圈故障源自裂纹,因此提高套圈的裂纹检测能力对提高轴承质量具有重要的工程意义[2]。

目前,轴承套圈缺陷检测方法主要有磁粉探伤[3-4]、涡流检测[5-6]、漏磁检测、超声波检测[7-8]以及机器视觉检测[9-11]等。

漏磁检测广泛应用于各类铁磁性材料的检测中,对表面、近表面缺陷的检测能力较好,而且灵敏度高,便于实现自动化[12],越来越多的学者致力于实现漏磁检测在轴承套圈上的应用:文献[13]使用与旋压面啮合的极靴导套构成U形磁化器,实现了轮毂轴承旋压表面和内部的缺陷检测,并采用磁感应头探针实现轴承内部微裂纹的检测[14];文献[15]为将漏磁法应用于套圈的微细裂纹检测,提出了一种多轴承套圈内外壁双面同步高速漏磁检测方式,解决了轴承套圈大批量、高速、高精的检测需求;文献[16] 提出了一种基于交直流复合磁化的漏磁检测方法,实现了轴承套圈快捷、全面、精细的自动化无损检测。

以上研究从不同方面实现了轴承套圈的漏磁检测,但没有对表面曲率半径变化的轴承套圈进行深入研究。在实际应用中发现,相同大小的周向裂纹在不同曲率半径处的漏磁信号存在差异,可能导致同尺寸不同位置处裂纹的漏磁检测结果不一致,无法依据漏磁检测结果对实际裂纹尺寸做出准确的量化分析,影响轴承套圈漏磁检测结果的判别。因此,本文研究轴承套圈表面曲率半径对周向裂纹漏磁信号的影响规律,提出局部磁化方式和信号补偿方法,以提高套圈裂纹漏磁信号的一致性和检测能力。

1 轴承套圈表面曲率半径对周向裂纹漏磁信号的影响

如图1所示,轴承内、外径面(表面1)均为曲率半径恒定的圆柱面,但不同型号轴承的滚道面存在曲率半径的恒定和变化2种情况,例如表面2的曲率半径恒定,表面3的曲率半径则沿轴向逐步变化。在轴承实际应用中,套圈与滚子的接触表面承受载荷作用且相互摩擦,对该表面的裂纹检测能力有着更高的要求。

根据漏磁检测中裂纹的垂直检出理论,激励磁场与裂纹平行时几乎没有漏磁场,激励磁场与裂纹垂直时产生的漏磁场最大。检测轴承套圈周向裂纹时,需要进行轴向磁化,目前常采用环形线圈法和U形磁轭法,当套圈表面曲率半径变化时,环形线圈无法生成平行于内表面的磁场,而U形磁轭的磁场方向灵活多变,可以很好满足套圈表面曲率半径变化的磁化要求。

轴承内、外圈存在对称关系,同一检测装置可以同时实现内、外圈的检测,因此本文以外圈作为研究对象,其轴向磁化模型如图2所示,磁化器固定不动,套圈经过磁化后,探头沿平行于内表面的扫查路径移动,获取表面上方连续的磁场强度变化。另外,磁化器由U形铁芯缠绕线圈制成,可通过更换磁轭满足不同规格轴承套圈的磁化需求。

图2 轴承套圈轴向磁化示意图

为了进一步观察滚道面的磁化特性,采用COMSOL Multiphysics 5.4有限元仿真软件建立仿真模型(图3)。套圈的轴向宽度为50 mm,大端壁厚为25 mm,小端壁厚为5 mm,滚道面曲率半径范围为70～90 mm,为消除两端磁极对磁力线走向的影响,磁轭两端厚度设置与套圈厚度一致,宽度为70 mm,高度为50 mm,中间的厚度为5 mm。

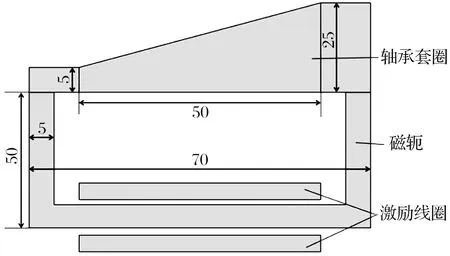
图3 轴承套圈轴向磁化仿真模型

当加载的电流激励为15 000安匝时可将套圈饱和磁化,改变右端壁厚可以得到曲率半径恒定和变化时的磁场分布,结果如图4所示: 曲率半径恒定时,套圈的磁感应强度基本一致;曲率半径变化时,套圈的磁感应强度从左到右逐渐降低。

(a) 曲率半径恒定

为进一步观察套圈近表面的磁化特性,提取曲率半径恒定和变化时套圈近表面的磁感应强度,距表面0.1 mm处的磁感应强度曲线如图5所示:套圈滚道面曲率半径恒定时,磁感应强度基本保持一致;套圈滚道面曲率半径变化时,随滚道面曲率半径的不断增大,磁感应强度也不断增大,套圈在不同曲率半径处存在严重的磁化不均。

(a) 曲率半径恒定

为研究滚道面曲率半径对周向裂纹信号的影响,在轴向磁化仿真模型的基础上设置相同尺寸的7个矩形周向裂纹,如图6所示。进行裂纹宽度和深度均为0.5,0.3,0.1 mm的3组试验,相邻裂纹的间隔为5 mm,提离距离为0.1 mm,沿提取路径获取曲率半径恒定和变化时套圈的漏磁信号及其幅值,结果如图7所示:对于相同大小的矩形裂纹,曲率半径恒定时,套圈的漏磁信号基本一致;曲率半径变化时,套圈的漏磁信号随着曲率半径的不断增大而增大,基线信号也存在偏移。

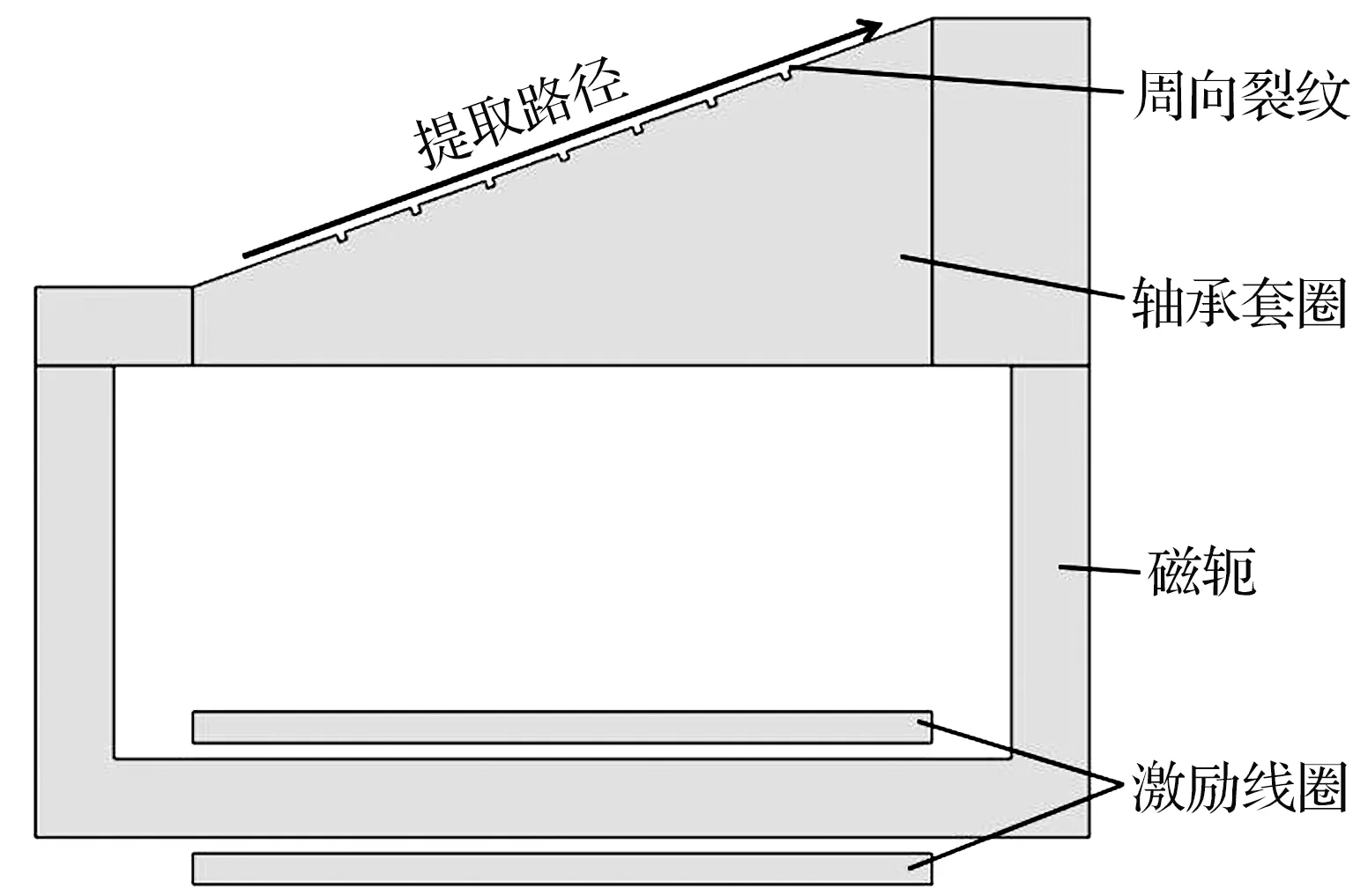
图6 轴承套圈周向裂纹漏磁仿真模型

(a) 曲率半径恒定

采用信号幅值的相对改变作为评定信号一致性的指标,其定义为最大、最小信号幅值之差与最大检测信号幅值之比,即

(1)

式中:Bmax为信号幅值的最大值;Bmin为信号幅值的最小值。

ΔB越大,代表信号的一致性越差,当ΔB小于10%时可以不考虑信号的一致性问题。经计算,曲率半径恒定时, 3种裂纹套圈信号幅值的相对改变量分别为2.78%,3.67%,7.01%,均小于10%,因此当轴承套圈曲率半径恒定时,无需考虑曲率半径对裂纹漏磁信号的影响,之后的研究仅针对曲率半径变化的轴承套圈;曲率半径变化时,3种裂纹套圈漏磁信号幅值的相对改变量分别为93.37%,93.46%,94.69%,说明其一致性很差。由于不同尺寸裂纹的漏磁信号变化规律基本一致,下文均以0.5 mm的缺陷为例进行更深入的分析。

另外,为提高裂纹漏磁信号的一致性,从以下方面进行优化:1)优化磁化器结构,降低套圈在不同曲率半径处的磁化不均匀程度,从源头上提高裂纹漏磁信号的一致性;2)分析滚道面曲率半径对裂纹漏磁信号的影响规律,拟合出信号补偿系数,进一步提高裂纹漏磁信号的一致性。

2 周向裂纹磁化器优化方法

根据上文的结论,为保证检测信号的一致性,关键是在套圈近表面建立均匀的磁场。在套圈磁化过程中,根据基尔霍夫第一定律,磁路的任一节点处,进入该处的磁通与离开该处的磁通的代数和为零,即

BiSi=BjSj,

(2)

式中:Bi,Bj分别为滚道面上第i,j处的磁感应强度;Si,Sj分别为第i,j处的横截面面积。

横截面面积S与磁感应强度B成反比,由于套圈滚道面曲率半径沿轴向从左到右(图3)不断降低,横截面面积逐渐增大,因此磁感应强度不断减小,横截面面积差异越大,磁感应强度差异就越大。为降低套圈横截面差异导致的磁化不均,将整体磁化优化为局部磁化,如图8a所示,探头与磁化器固定在一起沿着扫查路径移动,获取表面上方连续的磁场强度变化,探头外面设置屏蔽层用于屏蔽背景磁场的影响。

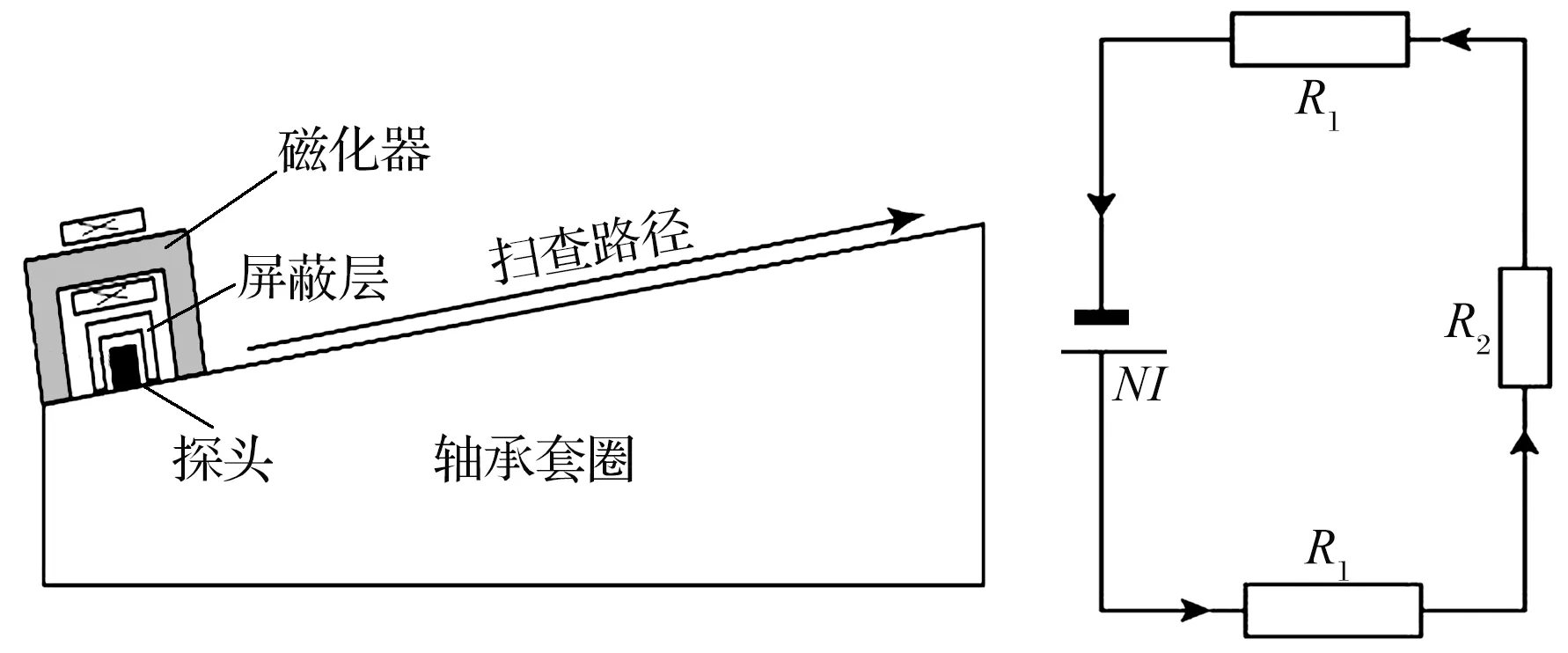
(a) 局部磁化示意图 (b) 等效磁路模型

轴承套圈局部磁化方式对应的等效磁路模型如图8b所示,在磁化器磁轭、轴承套圈组成的磁回路中取一条闭合的磁力线,则

(3)

式中:H为磁化强度;l为磁路长度;N为线圈匝数;I为线圈电流;εm为磁动势。

(4)

式中:Hc为磁化器铁芯的高度;φ为磁通密度;R1,R2分别为磁化器磁轭和轴承套圈的磁阻;D为两磁轭间距;μ为磁导率;S1为磁化器磁轭的横截面面积;S2为轴承套圈的横截面面积。

由(4)式可知:φ与Hc,D成反比,减小Hc和D可以增大套圈的磁感应强度;φ与S1,S2成正比,S1在套圈各处均一样,因此增大磁轭厚度会增大磁轭的横截面面积,从而提高套圈的磁感应强度;另外,根据(2)式可知减小D可以减小套圈的横截面差距,显著改善套圈的磁化不均。

为取得最佳的优化效果,通过有限元仿真对比两磁轭间距、磁化器铁芯高度、磁化器厚度不同取值时的磁化效果,采用最大、最小磁感应强度之差与最大磁感应强度之比作为衡量磁化不均匀性的标准,数值越大表明磁化越不均匀,由于局部磁化的范围小很多,当激励电流为6 000安匝时即可实现轴承套圈近表面的饱和磁化,仿真结果如图9—图11所示。

图9 不同磁轭宽度下的磁化效果

图10 不同磁轭高度下的磁化效果

图11 不同磁轭厚度下的磁化效果

由图9—图11可知:随着两磁轭间距的增大,套圈磁感应强度不断减小,磁化不均匀性不断增大;随着磁轭高度的增加,套圈的磁感应强度不断减小,磁化不均匀性则没有变化;随着磁轭厚度的增加,套圈的磁感应强度线性增大,磁化不均匀性不断提高。因此,为提高轴承套圈的磁化均匀性,两磁轭间距应尽量设计小,在保证磁感应强度前提下磁轭厚度应尽量设计小,磁轭高度则可根据被测套圈的内径调节。为满足实际应用中传感器的安装和尽量大的检测范围,选取磁化器两磁轭间距D=8 mm,磁轭高度Hc=10 mm,磁轭厚度T=2 mm,磁化电流为6 000安匝。

为验证磁化器优化后对裂纹漏磁信号一致性的改善作用,同样对7个宽度和深度均为0.5 mm的相同尺寸裂纹进行仿真计算,套圈滚道面不同曲率半径处的裂纹漏磁信号及其幅值如图12所示:磁化器结构优化后,裂纹漏磁信号的一致性得到了明显提高,信号幅值差异更小,基线的漂移情况也明显改善;裂纹漏磁信号幅值的相对改变量降低至47.27%,不到优化前的一半,充分说明套圈局部磁化方式可以显著提高裂纹漏磁信号的一致性。

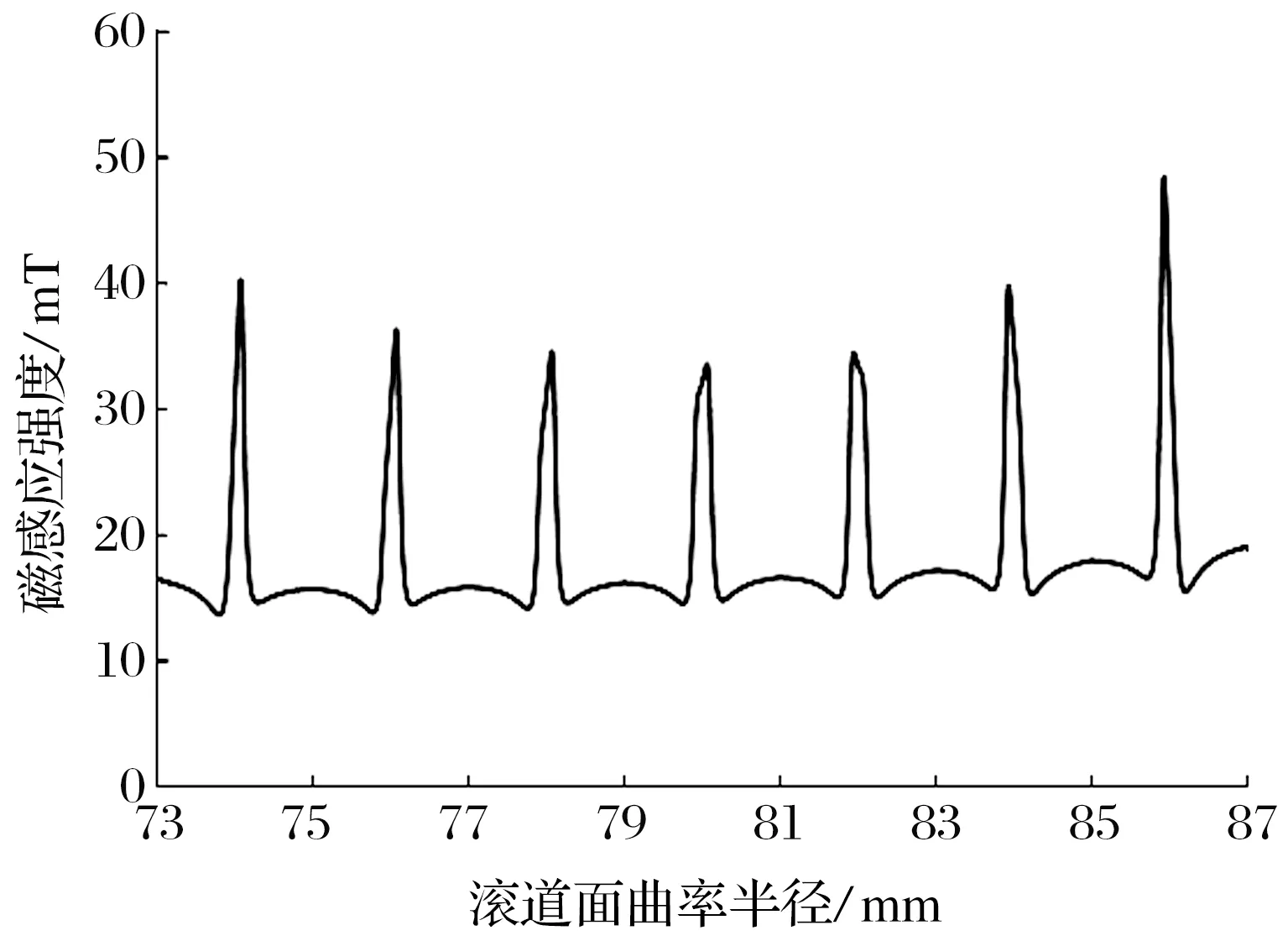
(a) 不同曲率半径处的裂纹漏磁信号

3 基于表面曲率半径特征参数的信号补偿方法

通过优化磁化器参数在很大程度上降低了磁化不均匀性,但裂纹漏磁信号幅值的对比分析表明仍存在一定的差距。轴承套圈滚道面曲率半径的变化是影响磁化效果的主要原因,但不论如何优化磁化器结构,两磁轭间距会一直存在,曲率半径的差异也会一直存在,采用局部磁化方式并不能从根本上消除磁化不均匀性。因此,本文基于轴承套圈滚道面曲率半径变化对裂纹漏磁信号的影响关系,运用回归拟合方法,提出一种基于表面曲率半径特征参数的信号补偿方法,拟合出曲率半径与漏磁信号两者间的补偿系数Kρ,进一步提高裂纹漏磁信号的一致性。

轴承套圈的横截面如图13所示,其外径R,接触角θ以及小端厚度d是确定的参数,滚道面的曲率半径r可以表示为

图13 轴承套圈横截面示意图

r=R-d-Rdif=R-d-xtanθ,

(5)

式中:x为补偿点距小端的距离。

由(5)式可知:套圈滚道面曲率半径r随x和θ的增大而增大,对于同一型号的套圈,其接触角是固定不变的,则曲率半径仅随x变化而变化;对于不同型号的套圈,曲率半径既受接触角θ的影响,也受距离x的影响。因此,为实现不同型号轴承套圈裂纹漏磁信号的一致性,将曲率半径分解为位置变化x和接触角变化θ分别进行补偿。

对于同一型号的套圈,仅需要考虑x对信号补偿的影响,保持接触角θ=20°不变,采用优化结构的磁化器进行轴承套圈的磁化,以图12中优化磁化器的裂纹漏磁信号的幅值作为拟合数据,对应的x分别为 10,15,20,25,30,35,40 mm,为消除其他磁化参数的影响,采用百分比的方式实现信号补偿,以第1个裂纹漏磁信号作为补偿基准,分别计算其他信号相对于第1个信号的补偿占比,即

(6)

通过MATLAB中的最小二乘法拟合得到裂纹信号补偿的拟合曲线(图14),拟合公式为

图14 基于位置变化的信号拟合曲线

Kρ(x)=-0.003 1x2+0.160 9x-1.270 9。

(7)

一般情况下,单列圆锥滚子轴承外圈的圆锥角为10°～30°,为实现轴承套圈漏磁信号在不同接触角下的一致性,设置轴承接触角分别为10°,12°,14°,16°,18°,20°,分别在x=15,20,25,30,35 mm处设置宽度和深度均为0.5 mm的裂纹,采用优化结构后的磁化器进行磁化,提取信号幅值绘制图像,结果如图15所示,随轴承接触角的不断增大,相同位置处的裂纹漏磁信号不断减小,大致呈线性变化。

图15 不同接触角下的裂纹漏磁信号幅值

以x=15mm处的漏磁信号作为拟合数据源,为消除其他磁化参数的影响,同样采用百分比方式实现信号补偿,以θ=10°作为补偿基准,通过MATLAB中的最小二乘法拟合,结果如图16所示,不同接触角下裂纹信号的补偿公式为

图16 基于接触角变化的检测信号拟合曲线

Kρ(θ)=0.012 1(θ-10°)-0.116 1。

(8)

上述分析获得了以x和θ作为单一变量的补偿公式,综合2个补偿公式可得到基于轴承套圈滚道面曲率半径特征参数的信号补偿系数,即

Kρ=Kρ(x)+Kρ(θ)+1=-0.003x2+0.161x+

0.012θ-0.508。

(9)

利用(9)式对磁化器优化后所得裂纹漏磁信号进行补偿,提取不同曲率半径处裂纹漏磁信号的幅值,与传统磁化器、优化磁化器的对比如图17所示:经过信号补偿后,位于两端的裂纹漏磁信号幅值改变不大,位于中间的裂纹漏磁信号的幅值大幅增加,相同尺寸裂纹的漏磁信号大致相同;经计算,裂纹漏磁信号幅值的相对改变量降低至9.8%,进一步提高了轴承套圈裂纹漏磁信号的一致性。

图17 信号补偿前后的裂纹漏磁信号对比

4 结束语

本文以轴承外圈为例,采用有限元仿真的方法研究了滚道面曲率半径对漏磁检测的影响规律,结果表明随着轴承外圈滚道面曲率半径的减小,近表面磁感应强度逐渐降低,导致不同曲率半径处的裂纹漏磁信号不一致,基线信号也存在偏移,信号幅值的相对改变量ΔB为93.37%,轴承内外圈存在对称关系,整个轴承套圈的滚道面均存在裂纹信号不一致的问题;为降低曲率半径对磁化效果的影响,提出局部磁化的方式,结合等效磁路计算和有限元仿真方法优化磁化器结构参数,将ΔB降低到47.27%,提高了裂纹漏磁信号的一致性;由于磁化差异无法完全消除,进一步提出一种基于表面曲率半径特征参数的信号补偿方法,拟合出曲率半径-漏磁信号两者间的补偿系数Kρ,将ΔB降低到9.8%,有效地改善了信号的一致性,提高了轴承套圈的周向裂纹检测能力,对于轴承套圈漏磁检测的应用具有重要指导意义,但补偿方法的实际工业应用效果仍需进一步验证。