微型稀薄气体润滑多叶轴承的静态性能分析

吴垚,郗文君,张彩丽,刘言松,曹巨江

(1.陕西科技大学 机电工程学院,西安 710021;2.施耐德(西安)创新技术有限公司 低压事业部,西安 710075)

随着超精密加工技术的不断革新,航空航天、国防军工、电力能源和低温制冷等领域的机械设备向着微型化、高精度、多功能、低能耗以及智能化等方向快速发展,使微型涡轮发动机、微型燃气轮机和微型涡轮增压器等微型透平旋转机械实现了各种能量间的转换,能源效率提升和微量动力输出[1-2]。微型气体轴承具有结构简单、气体介质性能稳定、回转精度高、摩擦功耗小及工作温度范围宽等优点,是微型转子的最佳支承形式[3]。微型多叶气体轴承的瓦间沟槽具有防止压力扰动扩散、削弱气膜交叉刚度和收集杂质粒子的作用,各周向槽视为一个“气泵”,可增加润滑膜厚和质量流量,减小轴颈-轴瓦表面的接触概率[4-5]。随着轴颈与轴瓦之间特征尺寸的减小,润滑气膜厚度接近或小于气体分子平均自由程时,微小间隙内稀薄气体流动问题与宏观尺度下的流动特性明显不同,必须考虑稀薄效应对微型多叶气体轴承性能的影响[6]。

目前,许多学者提出了不同的气体稀薄效应模型修正可压缩雷诺方程,研究了稀薄效应对超薄气膜润滑性能的影响。如1阶滑移模型[7]、2阶滑移模型[8]、1.5阶滑移模型[9]、 FK模型[10-11]及适用于任意克努森数的新滑移模型[12]等。文献[13-14]分析了稀薄效应对磁头/磁盘系统纳米薄膜润滑特性的影响,提出大轴承数和含有压力的剪切流项的可压缩雷诺方程的有限差分法。文献[15]利用分形函数表征微型气体轴承表面粗糙度,指出在偏心率和轴颈转速较高时轴承承载力的随机波动明显。文献[16]采用有限差分法和控制体积法求解了1阶速度滑移和温度阶跃边界条件的动量方程和能量方程,给出微小圆通道内层流的瞬态传热机理。文献[17]比较了连续模型、1阶滑移模型和新滑移模型对微型三瓦可倾瓦气体轴承各瓦块压力和承载力的影响,发现克努森数较大时,1阶滑移模型计算的承载力明显大于新滑移模型。

国内外在多叶滑动轴承润滑理论方面也取得了重要进展:文献[18]运用施图姆-刘维尔(Sturm-Liouville)理论和分离变量法,提出一种求解轴向槽径向滑动轴承非线性油膜力的近似解析模型;文献[19]通过影响系数法计算轴瓦弹性变形,研究了微沟槽水润滑轴承的弹流润滑性能,结果表明合适的沟槽深度在偏心率较小时可改善轴承润滑性能;文献[20]基于窄沟槽理论建立了人字槽气体轴承非线性行为的预测模型;文献[21]利用伽辽金有限元法分析了光滑、部分织构和完全织构表面对双瓣径向滑动轴承性能的影响,结果表明在压力形成区域有表面织构且沟槽长径比为1时会显著提高轴承的动力稳定性。

综上所述,现有微型气体轴承润滑性能的研究主要是针对圆柱气体轴承,有关微型多叶气体轴承静动态特性的理论还需要深入研究。本文采用兹曼稀薄效应模型修正气体润滑雷诺方程,推导考虑气体稀薄效应时微型多叶气体轴承静态性能的有限差分法,详细讨论瓦块分布位置和轴承参数对气膜压力、承载力和摩擦因数的影响,为微型旋转机械的性能预测和结构优化提供理论依据和技术支承。

1 微型多叶气体轴承结构及分析模型

微型多叶气体轴承一般由多个瓦块组成,最常见的是三叶气体轴承,瓦上承载和瓦间承载微型三叶气体轴承的模型和结构示意图分别如图1、图2所示,瓦上承载轴承的主要承载区位于底部第2个瓦块的中间截面处,而瓦间承载轴承的轴颈重量由下方2个瓦块共同支承。图中:O为轴承中心,Oj为轴颈中心;θ为偏位角,α为每个瓦块的瓦包角,ξ为轴向槽的槽宽包角,γ为轴承上方竖直线到第1个瓦块进气边的位置角,β为瓦块中间位置角,φ为从y轴负方向逆时针开始计算的气膜位置角;e为轴颈中心相对轴承中心的偏心距,R为轴颈半径,h为轴颈与瓦块间的气膜厚度,ω为轴颈转动角速度,Fx,Fy分别为轴承在水平、竖直方向的气膜合力。各瓦块内表面与轴颈表面在轴颈旋转方向上形成超薄气膜, 与微型圆柱气体轴承相比,微型多叶气体轴承有2个间隙:半径间隙Cb(瓦块内圆弧半径与轴颈半径之差)和装配间隙Cp(瓦块支点圆与轴颈半径之差)。

(a) 瓦上承载

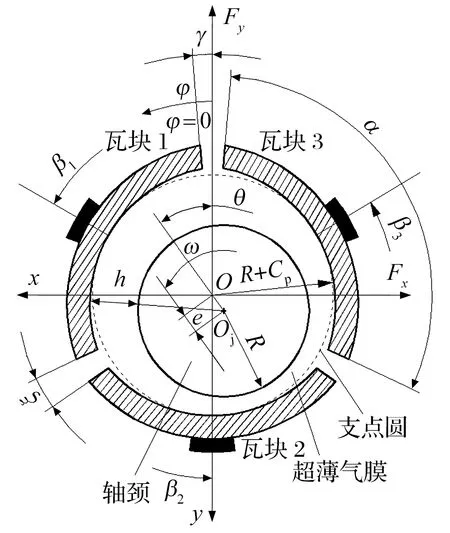
(a) 瓦上承载

由于黏性作用,轴颈旋转带动稀薄气体在微型多叶气体轴承表面形成超薄润滑气膜,从而为转子提供必要的支承。忽略润滑膜的惯性效应和热效应且假设稀薄气流为层流,根据纳维埃-斯托斯流体运动方程和连续性方程,结合牛顿黏性定律、雷诺假设并考虑稀薄效应的影响, 基于兹曼方程修正的超薄气膜润滑量纲一的雷诺方程为

(1)

P=p/pa,H=h/Cb,φ=x/R,η=z/R,

Kn=λ0/h,

式中:P为量纲一的气膜压力;p为气膜压力;pa为环境气体压力;H为量纲一的气膜厚度;h为气膜厚度;φ,η分别为量纲一的周向和轴向坐标;Λ为轴承数;μ为稀薄气体黏度;Q为考虑气体稀薄效应的Poiseuille流量比,即气体稀薄效应的修正系数[22];Kn为克努森数;λ0为气体平均分子自由程,取65 nm。

忽略瓦块厚度,微型多叶气体轴承各瓦块任一点量纲一的气膜厚度为

H=1+εcos(φ-θ)-mpcos(β-θ),

(2)

ε=e/Cb,

mp=1-Cp/Cb,

基于单片机的多功能视力保护器设 计 ……………………………………………………… 梁东丽，刘 颖（21）

式中:ε为轴颈中心相对轴承中心的偏心率;mp为预载荷系数。

相应的稀薄气体润滑方程量纲一的压力边界条件为

(3)

式中:L为轴承长度;φ0为从角起线到瓦块进气边的角度;φ1为从角起线到瓦块出气边的角度。

2 修正雷诺方程的有限差分解法

为快速求解超薄气膜润滑修正雷诺方程,将(1)式进行数学变换[23],令

(4)

则

(5)

求解微型多叶气体轴承的静态特性必须得到气膜压力分布,(5)式是二维非线性偏微分方程,传统解析法求解非常困难,本文利用有限差分法和连续超松弛法求解,将各瓦块内超薄气膜网格划分,每个节点处的压力值作为各阶差商的数据,通过求解所有节点处的压力值近似获得气膜压力分布情况。

气膜网格划分如图3所示,沿周向φ和轴向η分别均匀划分k和l格,网格间距Δφ=2π/k,Δη=2π/l;i,j分别为周向和轴向的网格节点编号;i=1,2,…,k+1;j=1,2,…,l+1。

图3 微型多叶气体轴承气膜网格划分

将(5)式进行中心和向前差分离散可得(6)式,将(6)式移项、合并同类项后变为Ai,jΠi+1,j+Bi,jΠi-1,j+Ci,jΠi,j+1+Di,jΠi,j-1-Ei,jΠi,j=Fi,j的形式,即

(6)

Λ(Si+1,j-Si-1,j)Δφ。

(7)

根据超松弛迭代公式求解上述方程组得到各瓦块量纲一的气膜压力分布。耦合计算气膜厚度及压力分布过程中稀薄效应的修正系数与气膜厚度紧密相关,需要同时不断循环更新Poiseuille流量比的结果,微型多叶气体轴承静态性能计算的基本流程如图4所示。当迭代计算气膜压力满足(8)式收敛准则即终止迭代过程,相对误差δ取1.0×10-6。

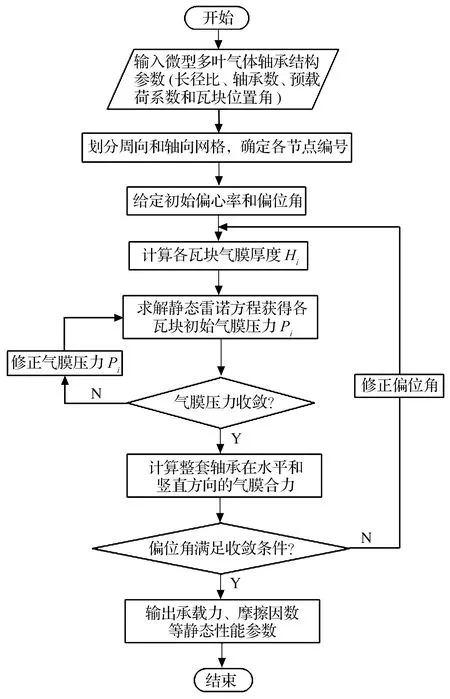
图4 微型多叶气体轴承静态性能计算的基本流程图

(8)

微型多叶气体轴承的静态性能由各部分圆弧瓦块共同决定,其在水平和竖直方向的气膜力为

(9)

则偏位角θ、量纲一的承载力CL和摩擦因数μb分别为

3 结果与讨论

为验证上述微型多叶气体轴承静态性能计算方法和自编程序的正确性,给出了长径比L/D=0.5,mp=0,Λ=0.5,α=115°,γ=38.9°时本文与文献[24]有关轴向槽气体轴承量纲一的承载力和偏位角的结果(表1),其中ε′为轴颈中心相对支点圆中心的偏心率(ε′=e/Cp)。文献[24]采用MATLAB中的PDE工具箱求解气体润滑雷诺方程。由表1可知,相同结构参数和运行参数下2种方法的结果非常接近,误差均在2.5%以内,验证了该算法的准确性和程序的可靠性。

表1 本文计算的承载力和偏位角与文献[24]的数值结果对比

本文选取微型多叶气体轴承的结构参数如下:半径间隙Cb为1 μm,瓦块的瓦包角α为100°,瓦上承载和瓦间承载的γ分别为-10°和50°,气体动力黏度为1.8×10-5Pa·s,环境压力pa为1.013×105Pa。

当ε′=0.6,L/D=0.1,mp=0.5,轴颈转速N为4×105r/min时,轴承的气膜压力分布如图5所示:预载荷系数较大时,微型多叶气体轴承的最大气膜压力高于相同结构参数的微型圆柱气体轴承,这是因为预载荷系数越大,瓦块内圆弧半径与轴颈半径的差值(装配间隙Cp)越小,相应的超薄气膜厚度也越小;瓦间承载微型多叶气体轴承的局部气膜压力最大,说明气膜压力峰值附近的瓦间沟槽吸入外部气体提高了润滑剂流量,很大程度降低了气体稀薄程度,从而提高了轴承的整体气膜压力。因此,微型多叶气体轴承可作为微型高速转子的有效支承。

(a) 微型圆柱气体轴承

当ε′=0.6,L/D=0.1时,轴颈转速和预载荷系数对轴承承载力的影响如图6所示:随着轴颈转速增大,承载力均近似呈线性增加的趋势,这是因为轴颈转速增加强化了轴承的动压效应,稀薄气流随转子高速旋转密度增大, 其稀薄程度有所降低;预载荷系数越大,微型多叶气体轴承的承载能力越强且承载力偏差越明显;当mp=0.5时,微型多叶气体轴承的承载力大于相同结构参数的微型圆柱气体轴承,说明预载荷系数较大时,微型多叶气体轴承可克服微型圆柱气体轴承承载力较大但稳定性差的缺点,满足微纳米尺度加工装配和超高速可靠运转的要求;瓦上承载微型多叶气体轴承的承载力比瓦间承载时的大,这是由于瓦上承载时的瓦块有效承载面积更大,连续性超薄气膜的范围较宽。

当ε′=0.6,L/D=0.1时,轴颈转速和预载荷系数对轴承偏位角以及摩擦因数的影响如图7所示:偏位角随轴颈转速的增大而逐渐减小,意味着轴承与转子在竖直方向的偏移量减小,有利于提升轴承的运转稳定性;预载荷系数越大,偏位角降幅越显著,瓦间承载时的偏位角明显小于瓦上承载时;摩擦因数随着轴颈转速的增大而线性增大,当mp=0.3和0.5时,微型多叶气体轴承的摩擦因数大于微型圆柱气体轴承,这是因为瓦块支点圆半径减小, 支点圆中心与轴承几何中心位置的不重合度增加,转子高速旋转导致的稀薄气流黏性剪切力增强;瓦间承载时的摩擦因数略高于瓦上承载时,这是因为轴向沟槽的“泵吸效应”增大了稀薄气体的流量,加剧了超薄气膜与轴颈表面的相互作用。

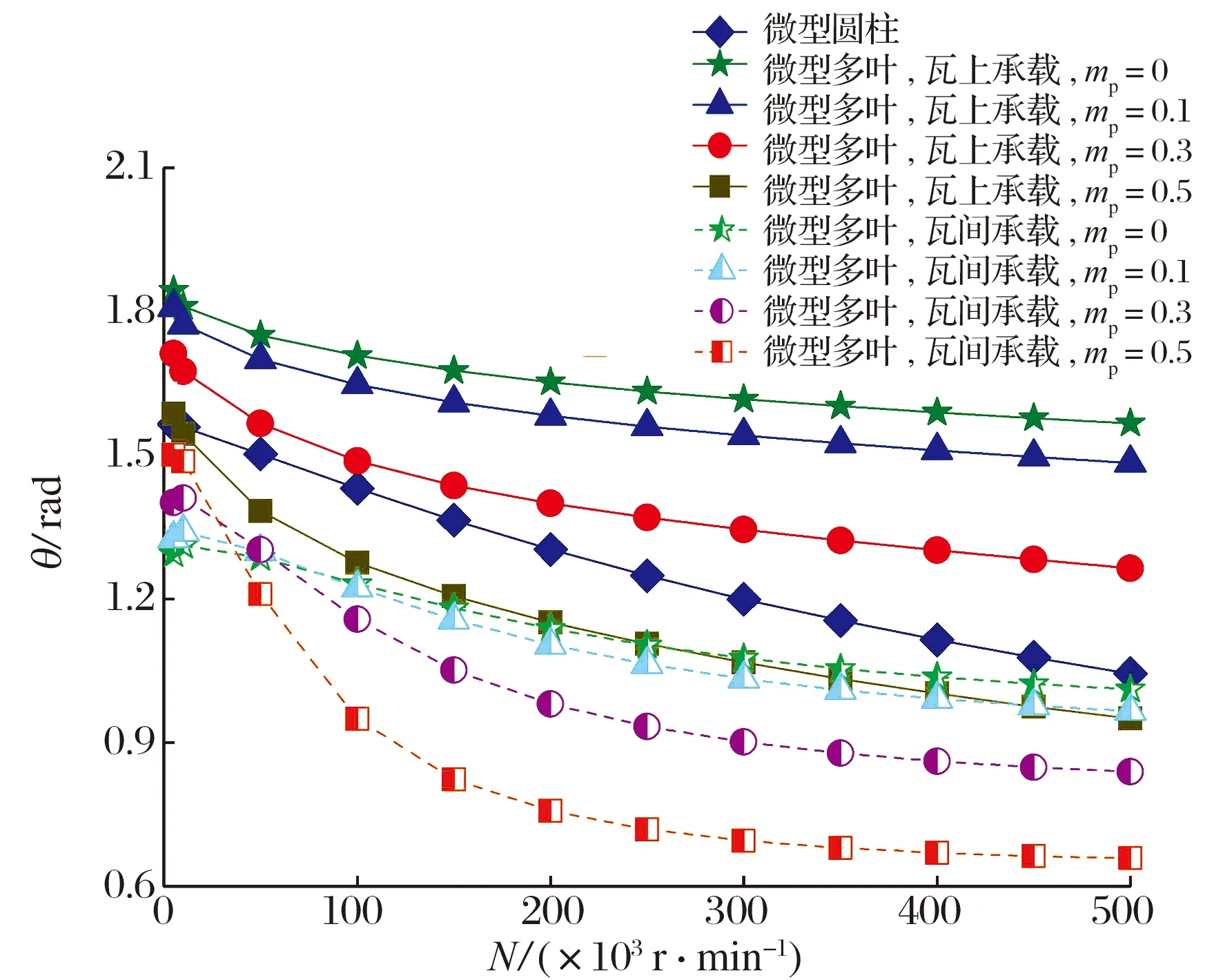
图7 轴颈转速和预载荷系数对轴承偏位角和摩擦因数的影响

当Λ=12,ε′=0.5时,长径比和预载荷系数对轴承承载力和摩擦因数的影响如图8所示:承载力均随长径比的增加而增加,长径比较小时,预载荷系数和瓦块分布位置的计算结果区别不大,而当L/D>0.4时,微型圆柱气体轴承的承载能力远高于微型多叶气体轴承,且随长径比增加,2种轴承的承载能力差距更明显,这是因为长径比增加对应轴承长度增大,瓦间沟槽破坏气膜连续性的弊端开始显现,动压效应减弱;由于超精密加工和硅片厚度的限制, 真实硅基微型气体动压轴承的长径比比传统气体轴承小1个数量级,通常为0.05～0.10,这表明长径比不是影响微型气体轴承润滑性能的主要结构参数;与轴颈转速对承载力的影响类似,相同长径比条件下,承载力随预载荷系数的增加而增大,瓦上承载时承载力更大;摩擦因数随长径比的增加而线性增加,预载荷系数较大时, 微型多叶气体轴承的摩擦因数高于微型气体圆柱轴承,而预载荷系数较小时,瓦块分布位置几乎对摩擦因数没有影响。

图8 长径比和预载荷系数对轴承承载力和摩擦因数的影响

当Λ=10,L/D=0.1时,偏心率和预载荷系数对轴承承载力和偏位角的影响如图9所示:随着偏心率的增加,承载力呈抛物线加速上升,这是由于偏心率越大,气膜厚度越小,形成压力场的压力越高,相应预载荷系数增加也可解释为气膜厚度的减小,提高了微型气体轴承的承载能力;相同偏心率条件下,瓦间承载时的承载力大于瓦上承载时,而且这种趋势在大偏心率时更突出,这是因为偏心率较大时,转子与瓦块的表面间隙极小,气体稀薄效应显著,从瓦间沟槽吸入的气体可有效降低气体稀薄程度,从而提高整体微型气体轴承的承载能力;但当ε′=0.9时,轴承内气膜厚度很小,从瓦间轴向槽内补充的气体不足以抵消稀薄效应对承载力的减弱作用, 此时微型圆柱气体轴承的承载力较高;偏位角随偏心率的增加而减小,说明承载力越大对应偏位角越小,偏心率ε′<0.4时,偏位角的变化幅度不明显。

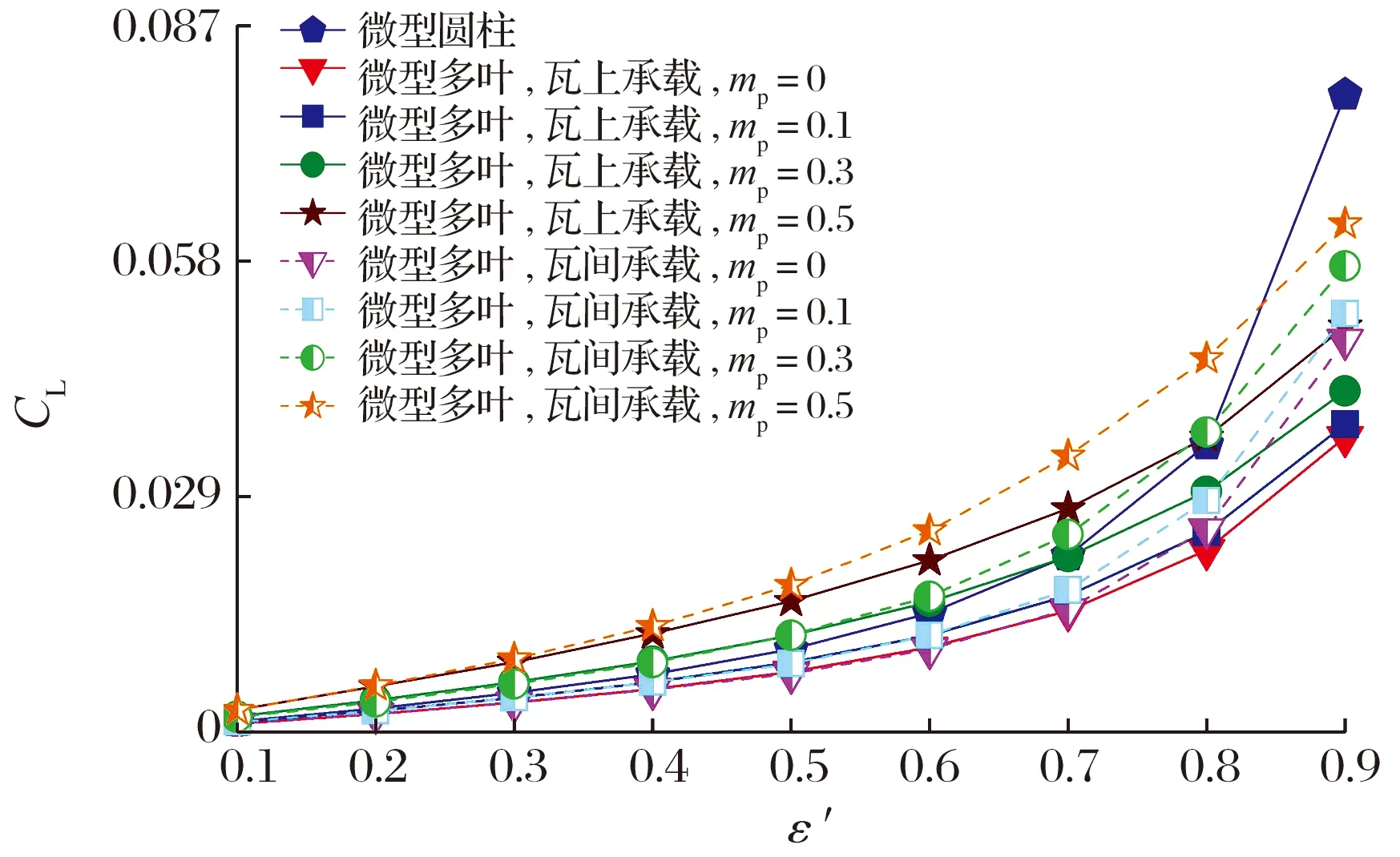
图9 偏心率和预载荷系数对轴承承载力和偏位角的影响

当Λ=10,L/D=0.1时,偏心率和预载荷系数对轴承摩擦因数的影响如图10所示:摩擦因数随偏心率增加而逐渐增大,这是因为偏心率变大导致气膜厚度减小,剪切应力提高;当ε′<0.5时,摩擦因数的增幅比较平缓,而偏心率较大时,摩擦因数快速增大;摩擦因数的增幅随预载荷系数的增加而显著增大;当ε′>0.5时,瓦间承载时的摩擦因数明显大于瓦上承载时,这是因为微型多叶气体轴承轴向沟槽泵吸的气体增大了膜厚方向速度梯度的剪切作用,同时气体稀薄程度的降低有效增大了气体黏度。

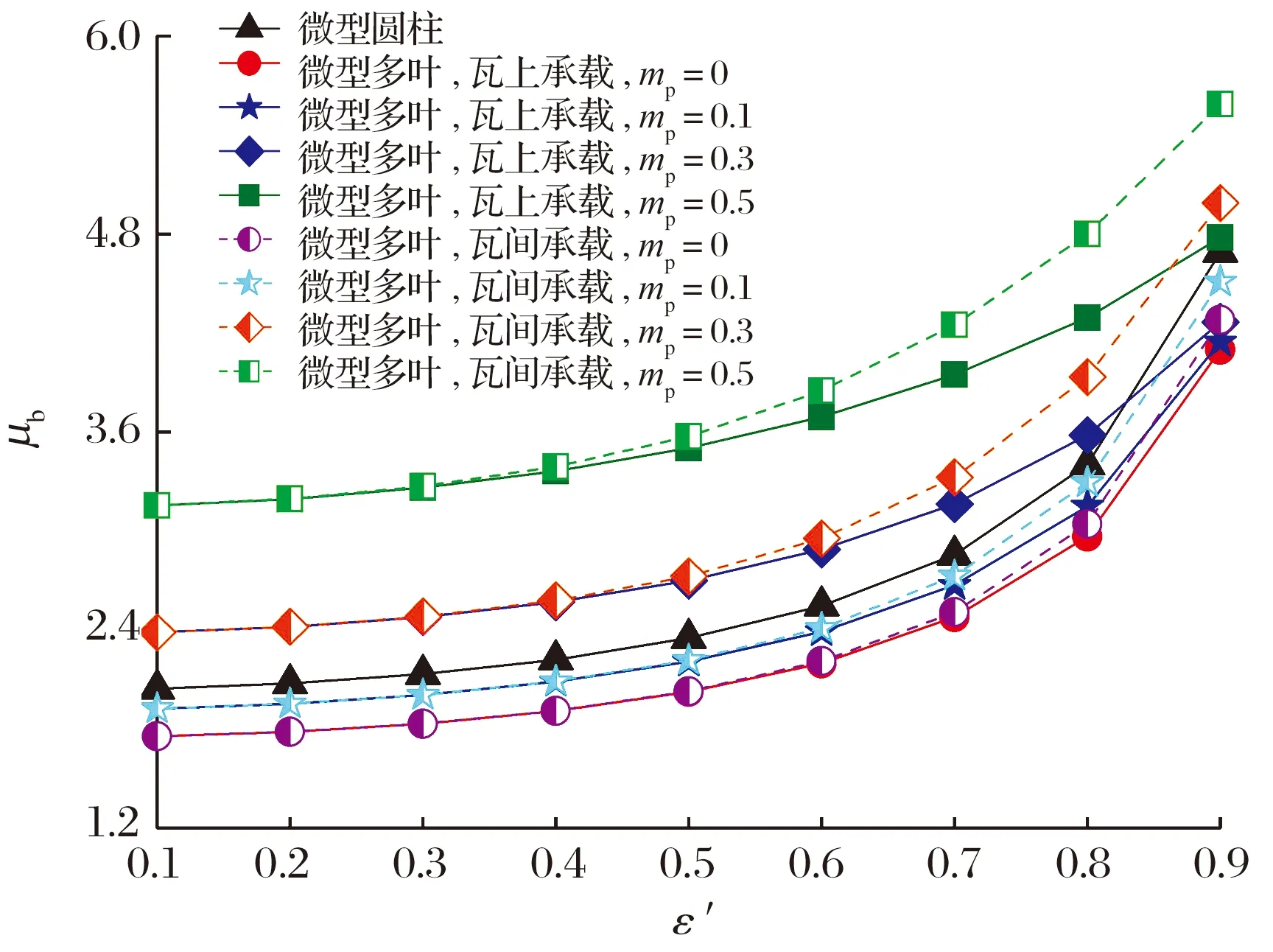
图10 偏心率和预载荷系数对轴承摩擦因数的影响

4 结论

本文介绍了微型多叶气体轴承稀薄气体润滑的静态修正雷诺方程及有限差分数值求解过程。研究了预载荷系数、瓦块承载方式和轴承参数对轴承静态性能的影响规律,得到以下结论:

1)当轴颈转速、偏心率和预载荷系数增加,瓦间沟槽吸入外部气体大幅降低了气体稀薄程度,气流相互作用增强,膜厚方向速度梯度的剪切作用加剧,瓦间承载微型多叶气体轴承的气膜压力最大,瓦上承载次之,微型圆柱气体轴承最小,而且瓦间承载时的摩擦因数大于瓦上承载时。

2)随着轴颈转速和长径比的增加,承载力均近似线性增加,这是因为提高轴颈转速增强了轴承的动压效应和稀薄气流的密度,增加长径比增大了各瓦块的承载面积。

3)承载力随偏心率的增加呈加速上升的趋势,当偏心率接近0.9时,瓦间沟槽泵吸外部气体提高承载力的作用要弱于气膜厚度减小带来稀薄效应降低承载力的作用,这时微型圆柱气体轴承的承载力较大。