噪声干扰下的CCSD-CNN轴承故障诊断方法
2023-10-17李辉徐伟烝
李辉,徐伟烝
(天津职业技术师范大学 机械工程学院,天津 300222)
随着人工智能的发展,深度学习在机电设备智能运维领域得到了广泛关注[1-3],故障诊断领域涉及的主要深度学习方法主要有自编码器(Auto Encoder,AE)[4]、卷积神经网络(Convolutional Neural Networks,CNN)[5]、深度信念网络(Deep Belief Network,DBN)[6]、循环神经网络(Recurrent Neural Networks,RNN)[7]和深度迁移学习(Deep Transfer Learning,DTL)[8]等。卷积神经网络充分利用了局部连接、权值共享和下采样等技术,不仅能有效避免参数过多导致的过拟合,而且运算效率较高,因此在故障诊断领域的应用较多[1]。
卷积神经网络常使用二维图像作为输入层,应用中通常采用信号预处理方法将一维振动信号转化为二维图像:文献[9]使用短时傅里叶变换(Short Time Fourier Transform, STFT)将电机轴承一维振动信号转换成二维时频谱图作为CNN的输入数据进行故障诊断;文献[10]提出一种基于深度卷积神经网络的故障诊断方法,利用短时傅里叶变换得到滚动轴承振动信号的二维时频谱并通过卷积神经网络自适应提取时频谱中的不同故障特征。短时傅里叶变换采用固定的窗函数,因而难以有效匹配变工况下轴承故障特征。文献[11] 将连续小波变换(Continuous Wavelet Transform,CWT)与CNN有效结合,应用于轴承和齿轮故障特征提取。文献[12]采用连续小波变换构建轴承振动信号的时频图并利用卷积神经网络实现自动模式识别。文献[13]利用小波包变换分解振动信号并重构小波包时频图,通过深度卷积神经网络实现不同工况、不同故障程度及故障类型轴承的模式识别。文献[14]利用离散小波变换构造时频矩阵,采用CNN进行特征提取,通过Softmax分类器实现故障分类。小波变换采用可调时频窗函数,能自适应地匹配轴承故障特征,但不同的小波母函数会得到不同的分类效果。在真实的工业场景下,采集到的数据除了被测轴承振动信号外,还往往混杂着各种各样的噪声,神经网络模型必须具有抗噪能力,才能精准地实现智能故障诊断[15-16]。
当机电设备中的轴承发生故障时,其振动信号往往是非线性、非平稳的非高斯信号,分析重点是其局部特征,而传统的时频信号处理方法难以有效处理该类信号[17]。另外,当设备工况(转速、载荷等)变化时,轴承振动信号中往往包含大量噪声和奇异值,CNN的特征提取能力也会显著下降[16]。振动信号的时频图刻画了非平稳信号的内在幅值和频率特征,信息刻画的越细微,越易于卷积神经网络进行信号特征的学习和提取,在噪声干扰下,基于短时傅里叶变换和小波变换等时频分析的信号预处理方法往往不能得到满意的诊断效果[18]。
轴承故障振动信号为典型的循环平稳信号[19-20],循环平稳方法能有效提取轴承的故障特征[21-22],谱相关密度(Spectral Correlation Density,SCD)能有效抑制信号中的高斯噪声,但当信号中含有非高斯噪声时,谱相关密度的性能会严重退化[23]。循环相关熵能有效处理非线性、非平稳、非高斯信号,在双频平面很好地刻画轴承的故障特征且具有很高的频率分辨率,能有效提取淹没在强噪声环境中的微弱信号特征[24-27],从而为CNN提供高质量的输入数据,提高传统CNN对非平稳、非线性、非高斯信号的自适应能力及其鲁棒性。因此,本文综合利用循环相关熵谱密度(Cyclic Correntropy Spectral Density,CCSD)和CNN的优点,提出了基于循环相关熵谱密度和CNN的轴承故障诊断方法(CCSD-CNN)。
1 CCSD-CNN故障诊断方法
1.1 循环相关熵
对于实信号x(t),其时变自相关熵函数可定义为
(1)
(2)
式中:τ为时间滞后量;E为数学期望;κσ(·)为满足Mercer条件的核函数,常采用高斯核函数;σ为高斯核函数的核长。
当实信号x(t)为循环平稳信号时,时变自相关熵函数Vx(t,τ)可展开为傅里叶级数形式,即
(3)
(4)
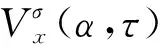
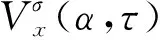
(5)
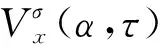
循环相关熵主要有以下性质:
1)循环相关熵利用了核函数κσ,核函数是一种非线性变换,将欧几里得空间的非线性数据转化为再生核希尔伯特空间的线性数据,因而循环相关熵能有效处理非线性信号。
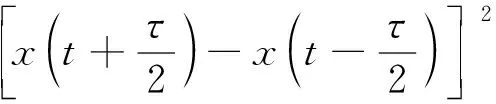
4)轴承故障振动信号为典型的循环平稳信号,属于一类特殊的非平稳信号,循环相关熵能在(α,f)构成的双频平面内有效刻画轴承故障特征且具有良好的频率分辨率,因此,循环相关熵能有效处理轴承故障诱发的非平稳信号[25]。
综上,充分利用循环相关熵的良好性能可以为卷积神经网络提供高质量的输入数据,有利于卷积神经网络对信号特征的学习和提取,优化CNN对非平稳、非线性、非高斯信号的自适应能力,提高CNN的鲁棒性和准确率。
1.2 卷积神经网络
典型的CNN是LeNet-5卷积神经网络结构[28],输入数据在经历多次卷积、激活和池化操作后被送入全连接层,并由输出层(分类器)输出模型的预测结果。本文提出的CNN模型借鉴LeNet-5卷积神经网络,模型参数见表1,包含2个卷积层,2个批归一化层,2个池化层,2个全连接层和1个Softmax输出层,卷积层和全连接层激活函数均采用ReLU函数。
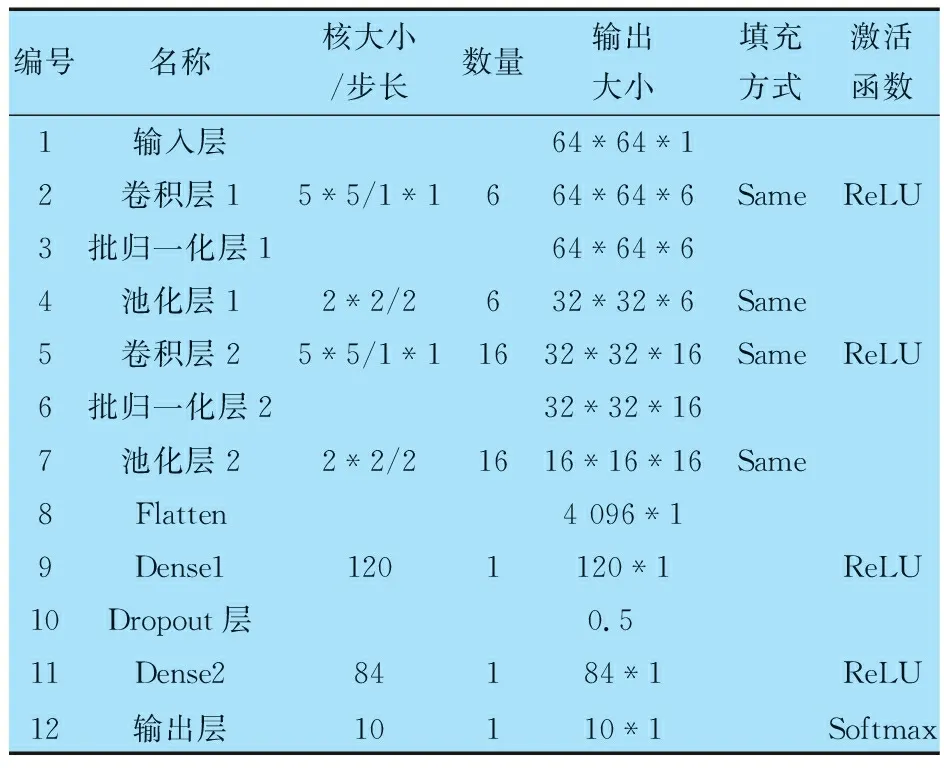
表1 卷积神经网络模型参数
1.3 CCSD-CNN故障诊断流程
如图1所示,CCSD-CNN轴承故障诊断方法的主要步骤为:
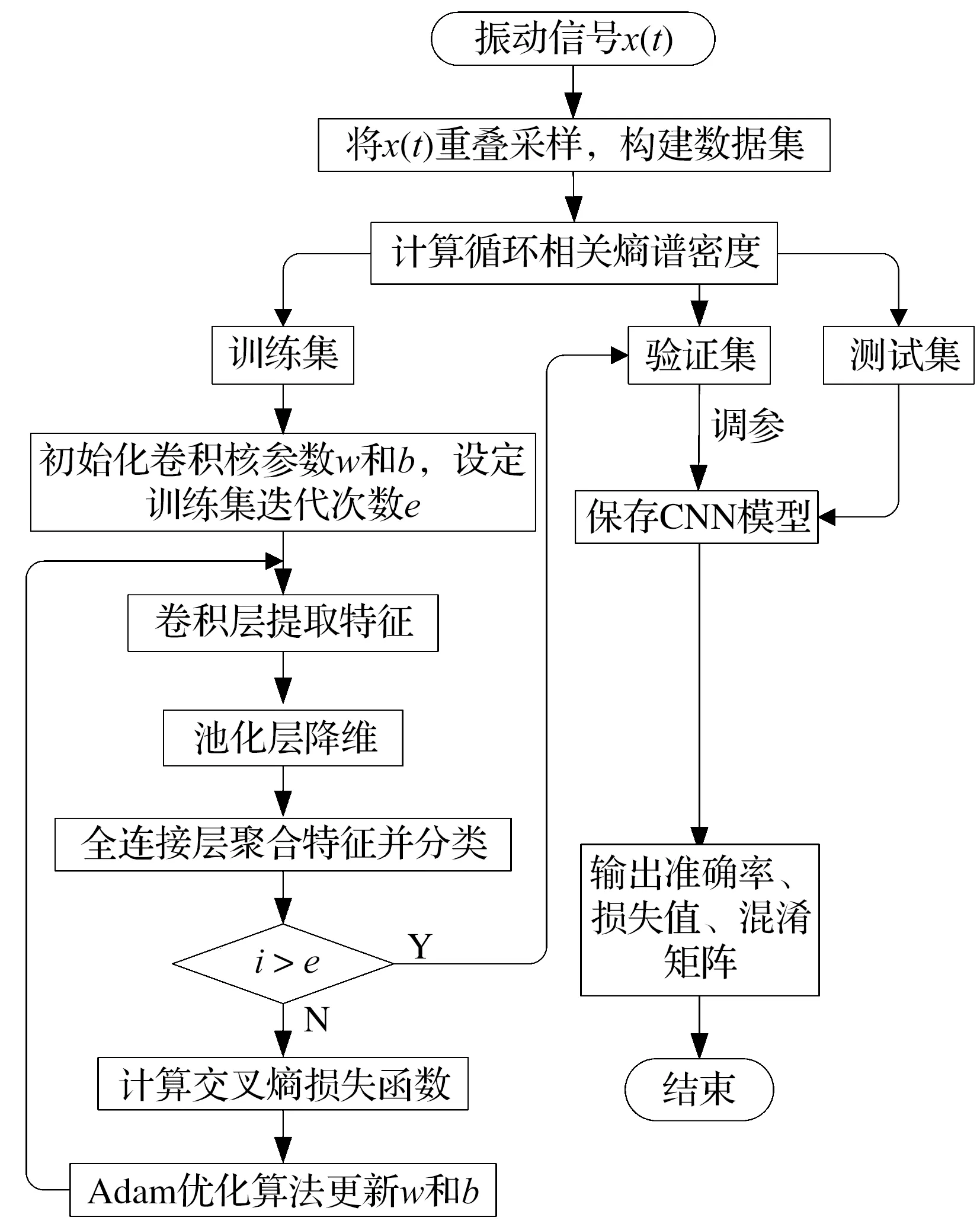
图1 基于CCSD-CNN的轴承故障诊断流程
1)对轴承故障振动信号进行重叠采样,进行数据集增广以构建轴承故障数据集,并将各样本数据归一化,将振动信号振幅控制在[0,1]。
3)将轴承故障数据集按6:2:2的比例划分为训练集、验证集和测试集。
2 基于CCSD-CNN的轴承故障诊断
2.1 CWRU电机轴承试验数据
将CCSD-CNN方法应用于美国凯斯西储大学(CWRU)滚动轴承数据集[29],振动信号采集对象为电动机驱动端(DE)的深沟球轴承,型号为SKF6205,采样频率为48 kHz。轴承故障类型分为钢球故障(BF)、内圈故障(IF)、外圈故障(OF),损伤直径分为0.178,0.356,0.533 mm,依据轴承故障类型和损伤直径将轴承钢球、内圈、外圈故障和正常状态分别标记为BF7,BF14,BF21,IF7,IF14,IF21,OF7,OF14,OF21,NC。
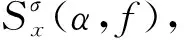
将验证集和测试集经CCSD预处理后输入训练好的CNN,验证集主要用于CNN模型参数的调整,测试集用于检验CNN的轴承故障准确率和泛化能力。按照CCSD-CNN轴承故障诊断流程从数据预处理、CNN特征提取识别、结果可视化分析3个方面进行详细试验分析与验证。
2.2 噪声干扰下CCSD故障特征提取
为验证循环相关熵在轴承故障特征提取方面的有效性,从数据集A中任选BF7,IF7,OF7和NC的一个样本,分别计算其谱相关密度(SCD)和循环相关熵谱密度(CCSD)。
2.2.1 原始振动信号
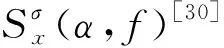
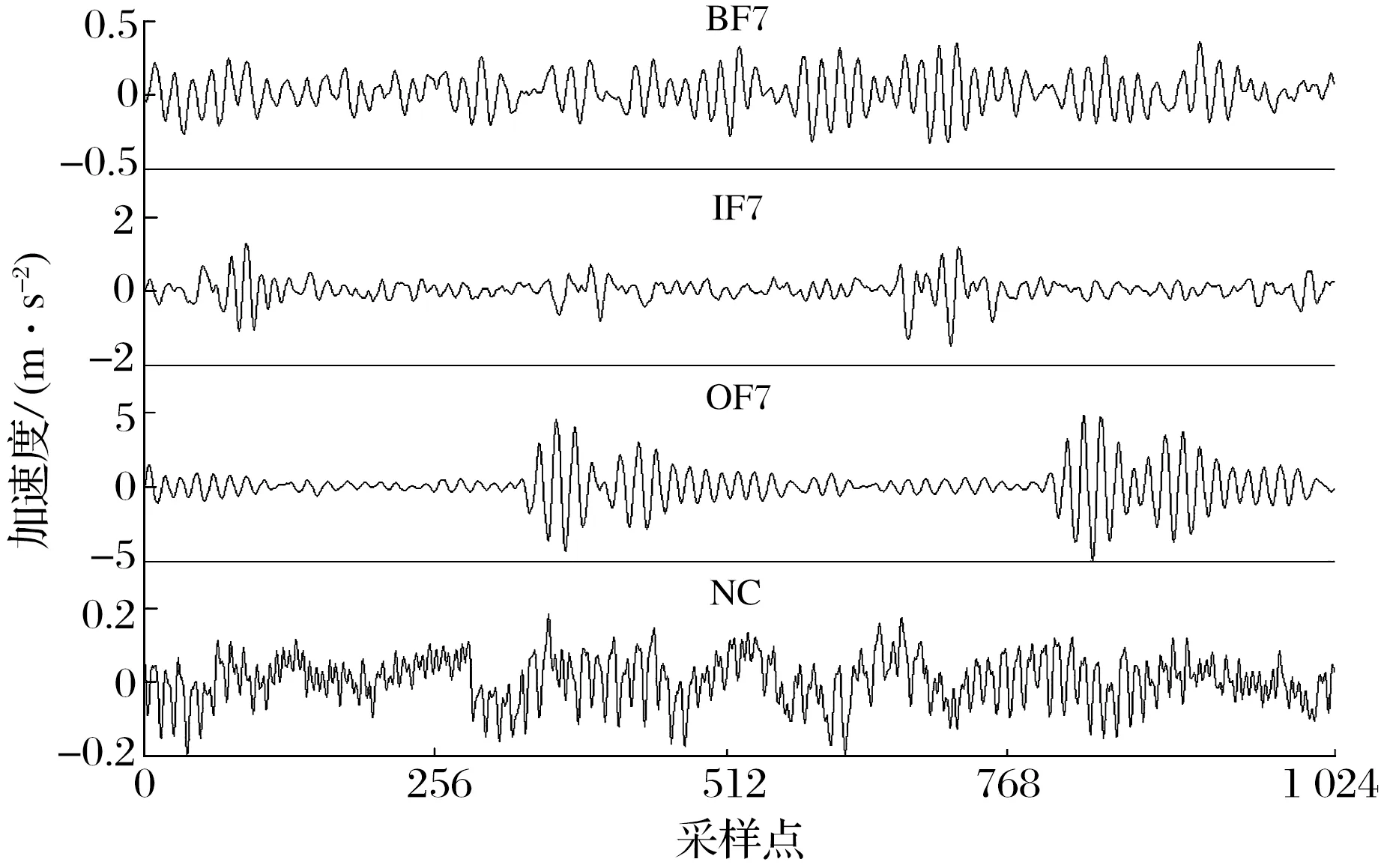
图2 轴承振动信号
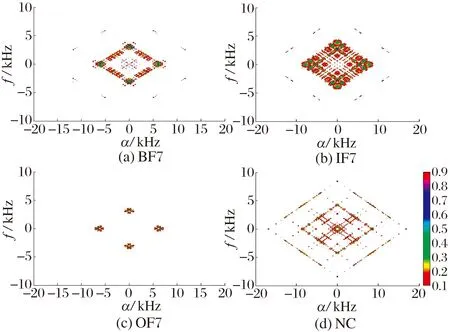
图3 轴承振动信号的谱相关密度
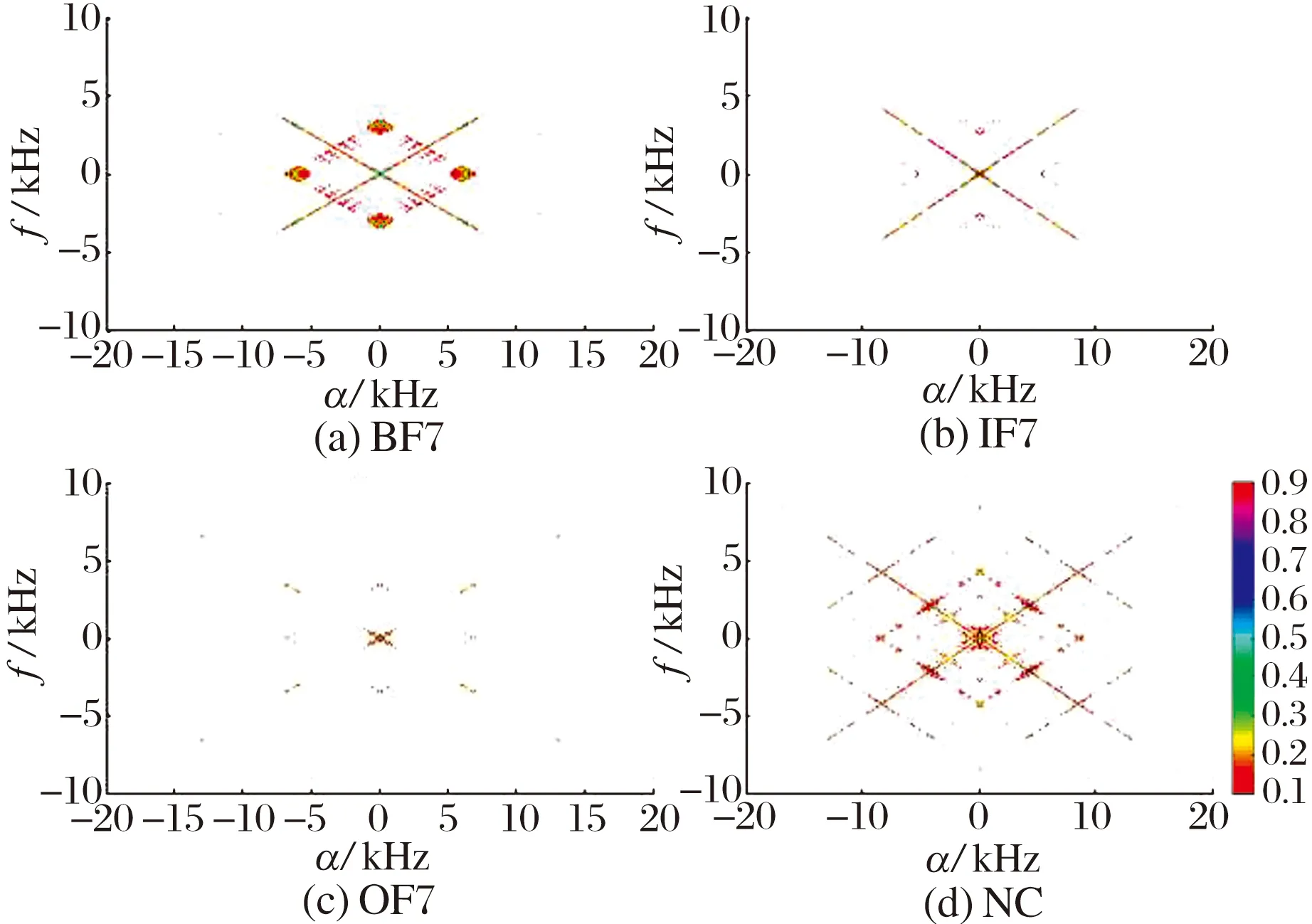
图4 轴承振动信号的循环相关熵谱密度
2.2.2 高斯噪声干扰
在轴承振动信号中添加信噪比(SNR)为-2 dB的高斯噪声,结果如图5所示:添加高斯噪声后,由于噪声对振动信号幅值具有平滑作用,减小了振动信号幅值之间的差异, 导致轴承故障产生的周期性冲击特征不再明显。
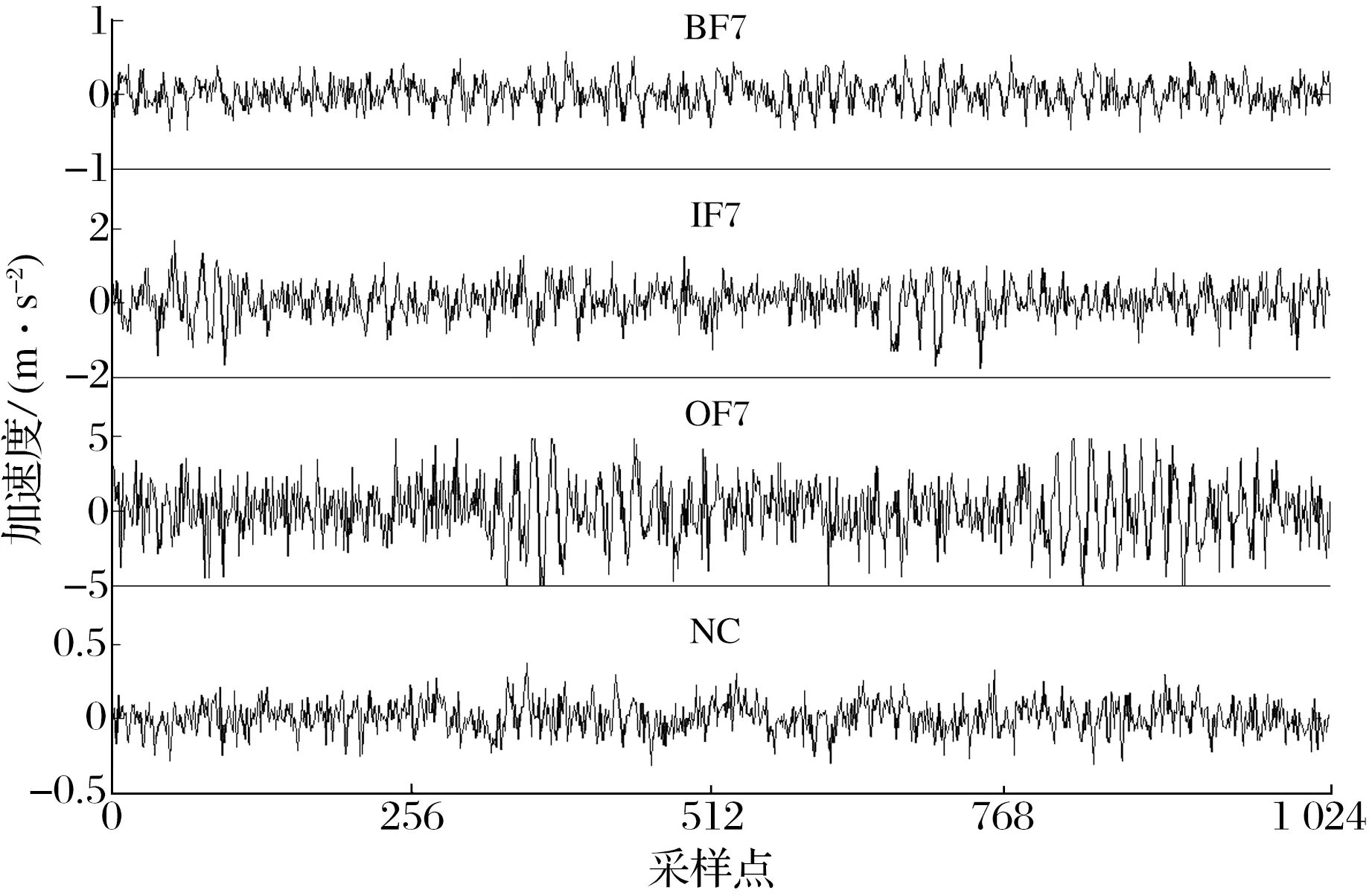
图5 添加高斯噪声后的轴承振动信号(SNR=-2 dB)
高斯噪声干扰下,轴承振动信号的谱相关密度和循环相关熵谱密度分别如图6、图7所示:由于噪声的影响,谱相关密度图中的菱形频谱结构更为明显,在更广泛的频率范围内存在非0幅值,尽管谱相关密度对高斯噪声具有自免疫能力,但高斯噪声的存在仍对谱相关密度产生了一定影响,降低了SCD的频谱分辨率;添加高斯噪声后,循环相关熵谱密度图的变化较小,而且比谱相关密度的频谱分辨率高,表明循环相关熵谱密度具有更好的高斯噪声抑制能力,在高斯噪声干扰下仍能有效提取轴承故障特征。
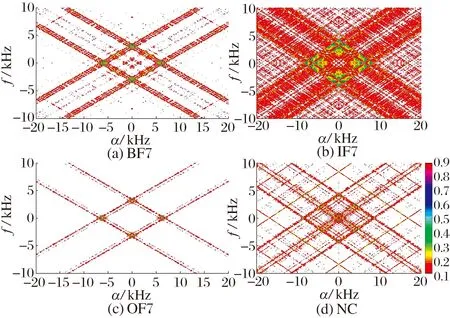
图6 轴承振动信号的谱相关密度(SNR=-2 dB)

图7 轴承振动信号的循环相关熵谱密度(SNR=-2 dB)
2.2.3 非高斯噪声干扰
随机选择10个幅值不等的脉冲信号模拟非高斯噪声,添加非高斯噪声后的轴承振动信号如图8所示:脉冲噪声的幅值远大于轴承振动信号的幅值,除外圈故障外,轴承振动信号基本上被脉冲噪声淹没,难以识别振动信号中的周期成分。
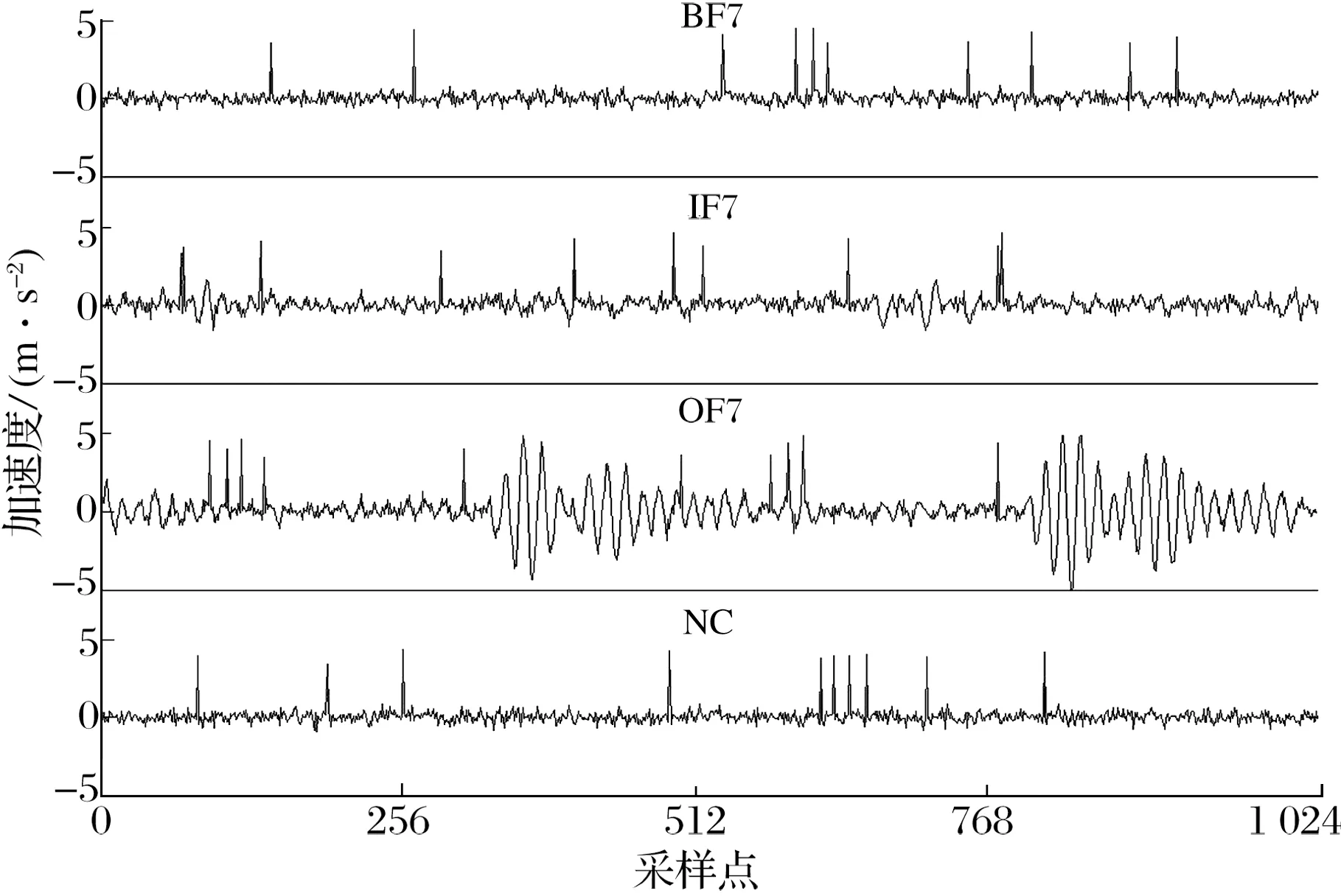
图8 添加非高斯噪声后的轴承振动信号
非高斯噪声干扰下,轴承振动信号的谱相关密度和循环相关熵谱密度分别如图9、图10所示:由于谱相关密度是基于信号的二阶统计量, 而脉冲噪声的二阶统计量并不存在,因此谱相关密度的性能退化,添加脉冲噪声后,谱相关密度图的频谱结构变得很模糊,频谱分辨率大大降低,很难提取轴承的故障特征;添加脉冲噪声后,循环相关熵谱密度图的变化较小,这是由于循环相关熵谱密度既包含信号的二阶统计量,又包含信号的高阶统计量,因此具有很强的非高斯噪声抑制能力,能在强脉冲噪声干扰下有效提取轴承微弱故障特征。
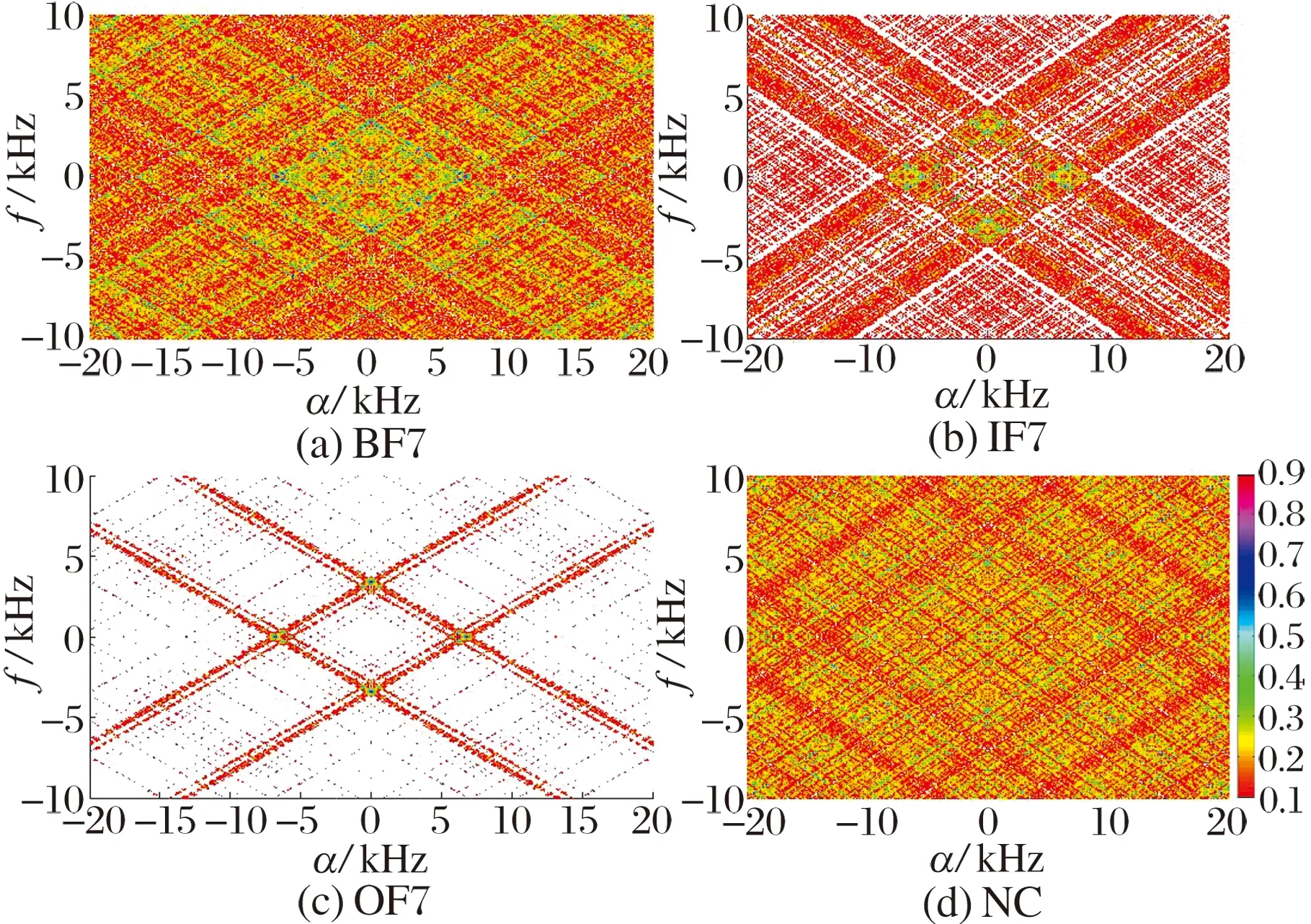
图9 添加非高斯噪声后轴承振动信号的谱相关密度
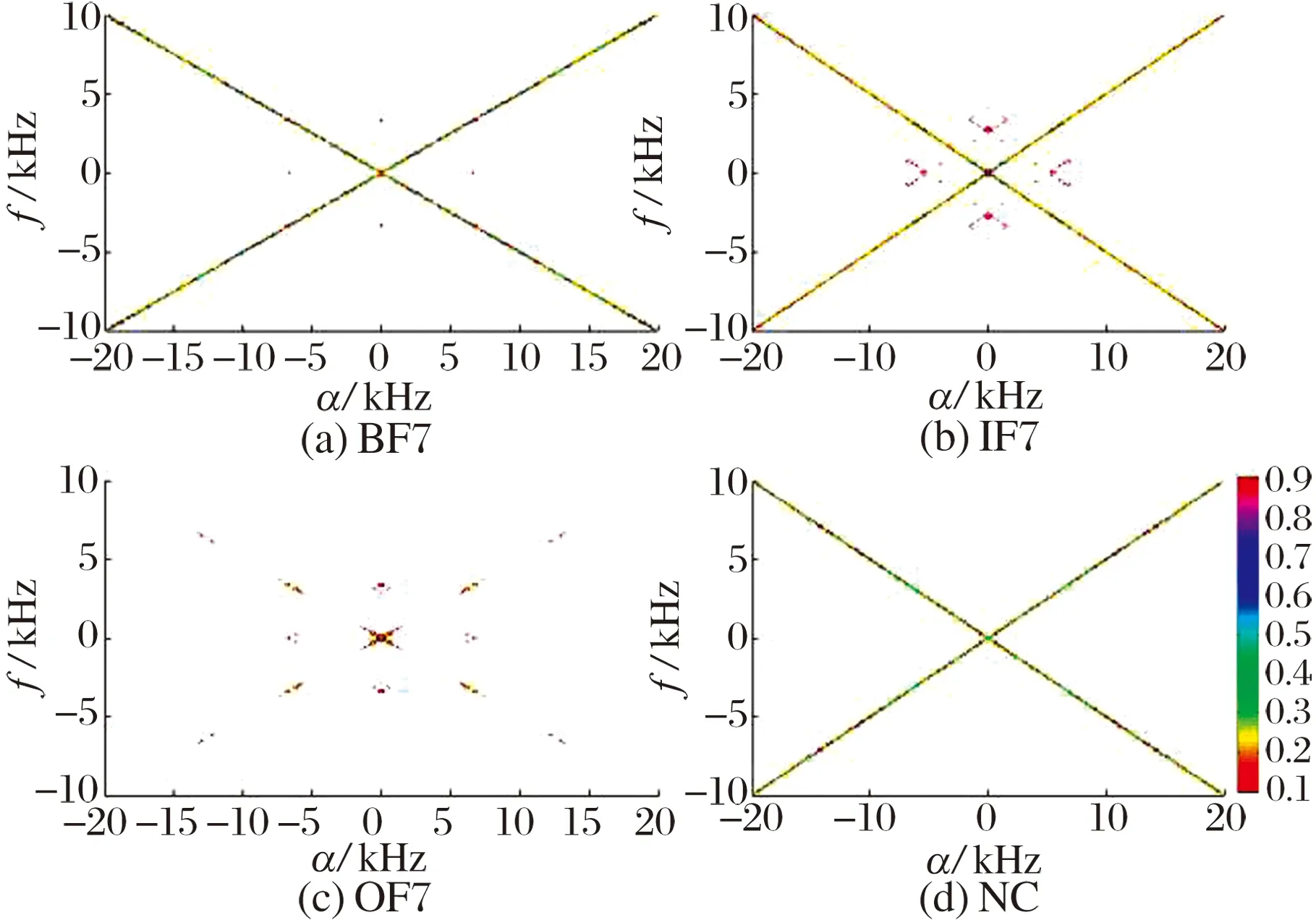
图10 添加非高斯噪声后轴承振动信号的循环相关熵谱密度
2.3 非高斯噪声干扰下CCSD-CNN故障诊断
对试验数据集的每个振动信号样本均随机添加10个幅值不等的脉冲信号,根据CCSD-CNN轴承故障诊断流程训练CNN,得到的准确率和损失值曲线如图11所示,在非高斯噪声干扰下,CCSD-CNN模型在训练迭代100次之后,故障诊断准确率高于95%,并且损失值逐渐趋近于0,表明CCSD-CNN模型稳定且训练速度较快。
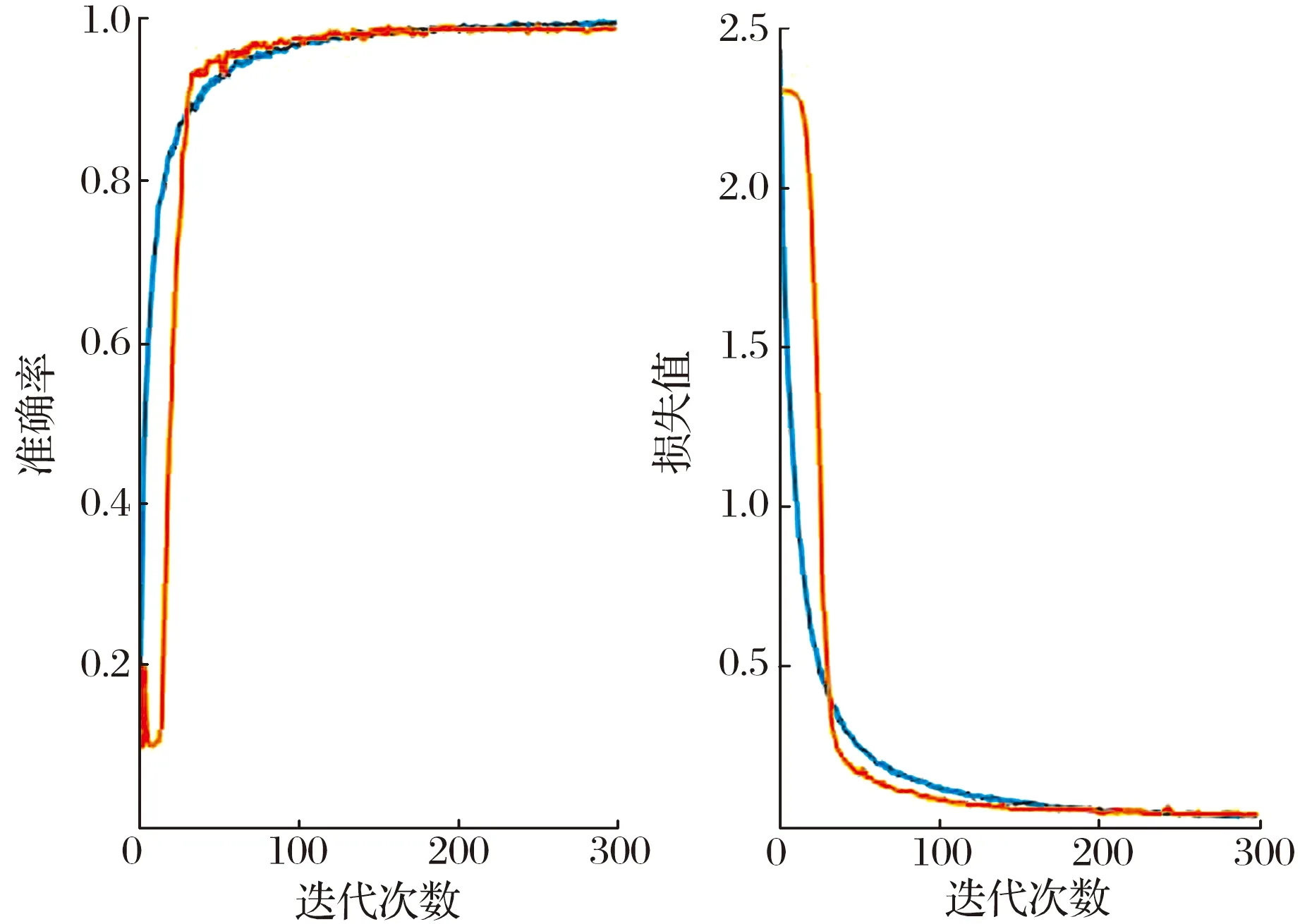
(a) 数据集A
添加非高斯噪声干扰后,将CCSD-CNN模型与STFT-CNN,CWT-CNN和SCD-CNN模型进行对比,其中STFT采用128点的Hanning窗,CWT采用Morlet连续小波变换,CCSD高斯核函数核长σ为1.72。各模型的诊断结果见表2(准确率取10次试验的平均值):在非高斯噪声干扰下,CCSD-CNN方法的准确率最高,3个测试集的平均准确率为98.53%,说明CCSD-CNN模型有效抑制了非高斯噪声,使得含非高斯噪声的振动信号经过CCSD预处理后,能获得高质量、高区分性的轴承故障特征图像,从而极大提高了CNN的故障特征提取能力。
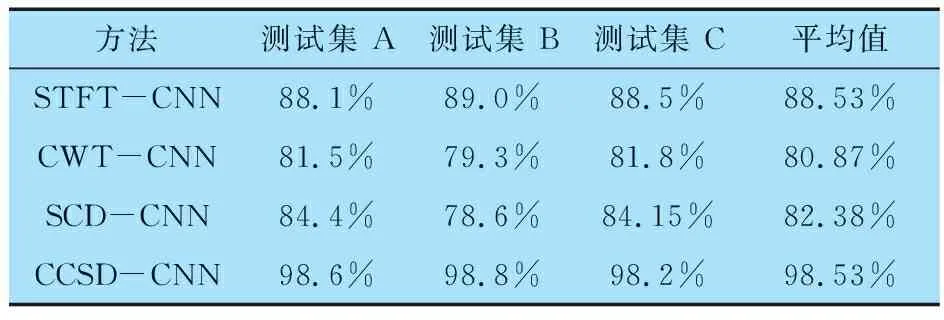
表2 非高斯噪声干扰下各模型的准确率
为进一步对比SCD-CNN和CCSD-CNN方法的特征提取能力,对添加非高斯噪声测试集的SCD-CNN和CCSD-CNN模型输出层特征进行t-SNE可视化[31-32],结果如图12所示:SCD-CNN模型只能将少数轴承故障进行分类,对多数轴承故障类型的辨别力较差,不同轴承故障类型间存在相互重叠,非高斯噪声干扰严重影响了SCD-CNN模型的特征提取能力,导致其鲁棒性变差;CCSD-CNN模型在测试集添加非高斯噪声的工况下,仍能清晰地划分不同类型的故障信号,10类不同故障信号之间只出现了少量的混叠,表明CCSD对非高斯噪声具有很强的抑制能力。因此,对含非高斯噪声的滚动轴承故障信号,CCSD-CNN方法比SCD-CNN具有更好的类内聚集性(类内间距小),且不同类别的间距较大,具有更好的非高斯噪声处理性能。
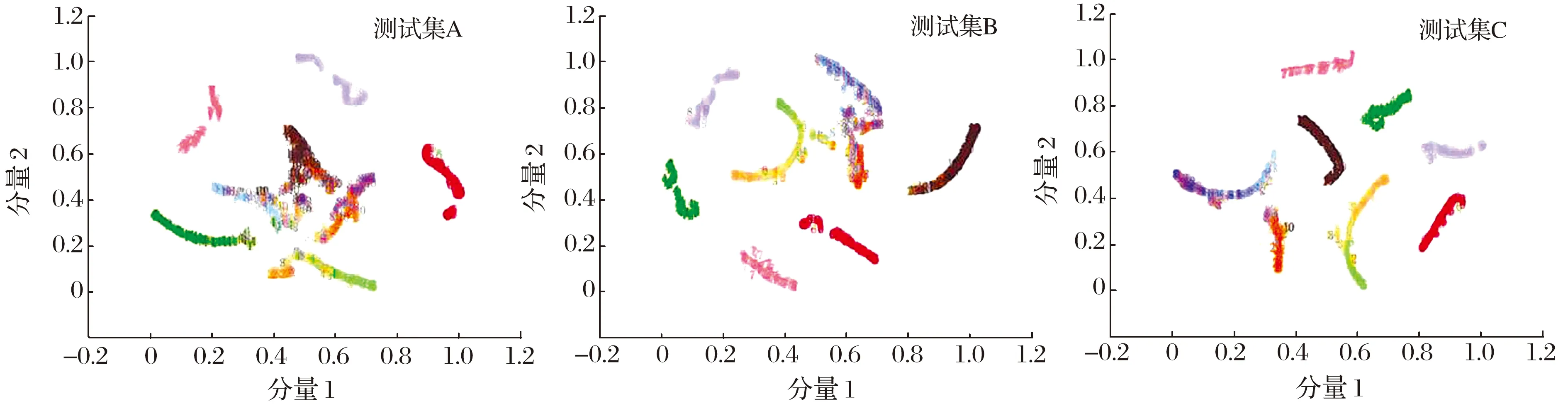
(a) SCD-CNN
2.4 高斯噪声干扰下CCSD-CNN故障诊断
试验数据集(3 hp)中添加不同信噪比(SNR分别为-6,-4,-2,0,2 dB)高斯噪声时,各模型的诊断结果(取10次试验的平均值)如图13所示:随着信噪比的提高,各模型的准确率都呈上升趋势,表明高斯噪声对CNN的诊断准确率有较大影响,但CCSD-CNN模型在不同条件下的准确率均高于其他模型。
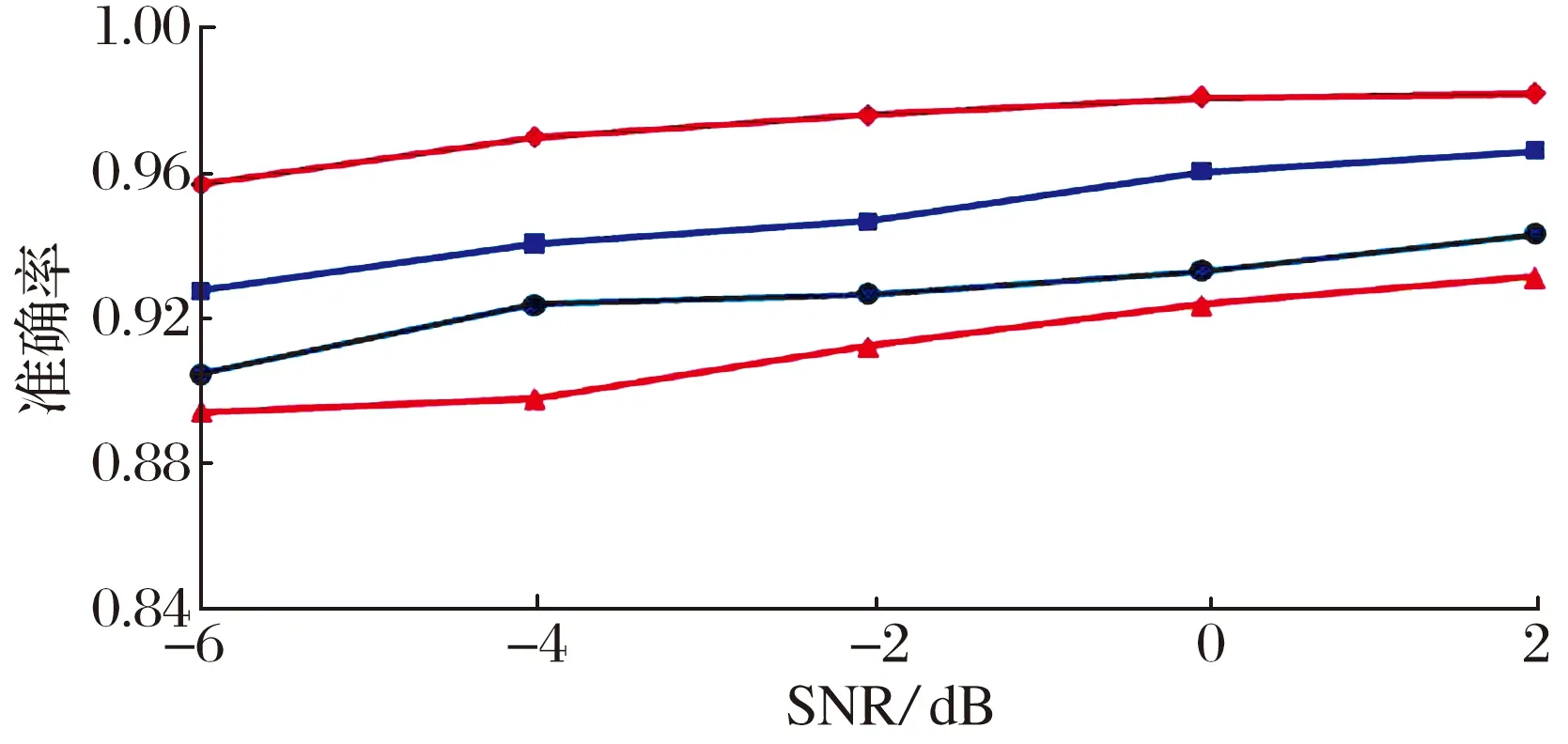
(a) 测试集A
3 结论
本文提出了基于循环相关熵谱密度和卷积神经网络的滚动轴承故障诊断方法,通过循环相关熵信号预处理有效增强了CNN的抗噪声干扰能力,提高了CNN网络的稳定性和诊断准确率:
1)从循环相关熵谱密度构成的双频平面(α,f)可以看出,不同的轴承故障类型具有不同的双频频谱特征且各故障状态的频率和幅值不同,即循环相关熵能有效刻画轴承不同故障状态,为CNN提供了高质量的输入数据。
2)在高斯噪声、非高斯噪声干扰下,CCSD-CNN模型的诊断准确率均高于SCD-CNN,STFT- CNN,CWT-CNN模型。
3)CCSD-CNN模型充分利用了循环相关熵的良好性能,改善了传统CNN对非平稳、非线性、非高斯信号的自适应能力,提高了CNN的鲁棒性。
