一种用于多视角雷达图像配准的改进RIFT算法

李焱磊 刘静博 刘文成 刘云龙 郭宇豪 王明明 梁兴东

（1.中国科学院空天信息创新研究院微波成像技术国家级重点实验室，北京 100190；2.中国科学院大学电子电气与通信工程学院，北京 100049）

1 引言

雷达图像配准是景象匹配导航［1］、图像融合［2］、三维成像［3］等很多应用中的关键步骤，其主要任务是求解不同时间、不同传感器或不同视角获取的多幅图像间的几何变换关系。目前，图像配准主要可以分为基于区域和基于特征的两类方法［4］。由于雷达独特的侧视和相干成像机制，其图像中存在局部非线性几何畸变和相干斑噪声，这使得基于区域的方法计算量大且容易产生局部极值［5］；与其相比，基于特征的方法计算量更小、鲁棒性更强，在雷达图像配准中应用更为广泛［5-10］。

尺度不变特征变换［11］（Scale-Invariant Feature Transform，SIFT）是最经典的基于特征的匹配方法，SIFT 对尺度、旋转的不变性以及对光照变化的鲁棒性，使其适用于多种不同类型的应用。目前，大量图像配准算法是以SIFT 为基础提出的［12-14］。在雷达图像配准领域，文献［5］利用双边滤波器替代SIFT 算法中的高斯差分算子进行尺度空间构建，在雷达图像中实现特征点准确检测；文献［6］使用指数加权均值比算子改进了SIFT 算法中的梯度计算方式，实现了雷达图像的鲁棒性配准。

由于雷达的侧视成像机制，同一目标在不同视角的雷达图像间可能存在明显的特征差异。尤其在目标相对于地面存在高程变化时，虽然现有技术可以利用数字高程模型校正图像中的几何失真，但在不同观测角度下，同一目标会表现出不同的散射特性，并对不同方向、大小的区域产生遮挡，即在不同视角的图像间存在非线性辐射畸变和不同的阴影特征。基于图像灰度梯度信息的SIFT 类配准算法在非线性辐射畸变和阴影差异的影响下，算法性能会出现大幅下降，无法稳定准确地完成多视角雷达图像配准。但是，在雷达图像匹配导航等实际应用中，多视角雷达图像配准是其无法避免的关键任务。同时，地表附属物丰富的区域图像纹理更加明显，与平坦地区相比可以检测出更多特征点，配准时更加关注这样的区域。因此，需要引入其他先进概念，研究对非线性辐射畸变和阴影差异具有鲁棒性的图像配准算法。

图像的灰度强度与灰度梯度信息对非线性辐射畸变十分敏感，相比之下，相位一致性（Phase Congruency，PC）特征与振幅无关［15］，当图像间存在辐射畸变时，其能够提供更鲁棒的特征检测与特征描述结果。基于相位一致性模型，文献［16］提出了相位一致性方向直方图（Histogram of Orientated Phase Congruency，HOPC），并在此基础上定义了相应的相似性度量，实现了多模态图像的配准，但其本质上是基于区域的匹配方法。文献［17］结合机器视觉中经典的矩分析方法实现了基于PC 的特征点检测，同时考虑到PC 易受噪声影响无法准确描述特征，选择构建最大索引图实现特征描述。但是，这种特征描述方法丢失了幅值、实部虚部关系等大量信息，容易产生错误匹配。除此之外，文献［18］提出了一种多尺度自适应分区相位一致性描述符，以应对图像间的几何变形与辐射畸变；文献［19］通过不同尺度上的最小PC矩提取图像中特征点，并使用相位一致性幅值与方向对特征描述符进行构建。然而由于图像间显著的辐射差异与阴影差异，将这些算法直接应用于多视角雷达图像配准时性能十分有限。

针对不同视角雷达图像存在不同阴影特征的问题，文献［20］利用数字高程模型（Digital Elevation Model，DEM），通过计算雷达视线与地面的相交次数对阴影区域进行检测，并在之后的匹配过程中为阴影区域增加掩膜，仅对非阴影区域进行匹配。文献［21］提出在大视角差异和地形起伏下提取山脊关键点，并使用关键点集的拓扑结构迭代实现关键点匹配，从而实现不同视角山区雷达图像的匹配。尽管取得了显著的成果，但上述方法均会受到应用场景的限制；当阴影区域是由房屋、树木等低矮地表附属物产生时，算法无法提取图像间的不变特征，进而无法实现多视角雷达图像的配准。

综上，为了实现存在丰富地表附属物的城镇、村庄等区域的多视角雷达图像配准，本文在RIFT的基础上，从提取视角不变特征和掩盖阴影差异的角度提出了一种改进RIFT算法。首先，本文设计了一种多特征描述方法，利用log-Gabor 滤波器实部和虚部的空间域性质对两种不同特征分别生成特征向量并进行匹配，使单一的特征变化不再对配准产生影响，增强算法对非线性辐射畸变的鲁棒性；其次，针对多视角雷达图像间阴影特性不同的问题，本文利用特征计算的中间结果对图像的阴影区域进行检测，并根据检测结果为特征向量添加掩模，最大限度地保留不随视角变化的特征信息。经过实验验证，本文所提方法能更有效地处理多视角雷达图像间的辐射畸变与阴影差异，实现图像的精确配准。

2 RIFT算法在多视角条件下配准性能分析

2.1 RIFT算法原理

RIFT 算法针对图像间存在非线性辐射畸变的多模态遥感图像配准问题提出。区别于使用图像强度或梯度信息的传统特征匹配方法（如SIFT等），RIFT 算法采用相位一致性模型，得到图像中对光照、对比度变化不敏感的频域特征信息，并在此基础上进行图像特征检测与描述，从而提高算法对非线性辐射畸变的鲁棒性，实现多模态图像的精确配准。RIFT 算法主要流程包括：特征检测、特征描述和特征匹配三部分；其中，特征检测和特征描述方法是其区别于传统算法且拥有良好性能的关键。

（1）特征检测

首先，使用二维log-Gabor 滤波器（2 Dimensional Log-Gabor Function，2D-LGF）对图像进行卷积，得到图像频率响应。2D-LGF 的空间域表达式可以写为［16］：

其中，滤波器的实部分量(x，y) 和虚部分量(x，y)分别被称为偶对称log-Gabor 小波和奇对称log-Gabor 小波。对于给定图像I(x，y)，利用2DLGF与图像进行卷积运算：

得到图像在尺度s和方向o上的振幅分量Aso(x，y)与相位分量φso(x，y)。

然后，利用相位一致性模型［4］求得相位一致性特征PC与方向o之间的关系：

式中，ωo(x，y)为加权参数；T为噪声补偿项；ξ是为了防止分母为零而设置的常量；·运算符中的值为负值时结果等于零，否则等于其本身；ΔΦso(x，y)为相位偏差函数。

最后，RIFT 算法根据相位一致性定义，参考经典的矩分析方法［22］，得到能够表征图像角点特征与边缘特征的最小矩图和最大矩图，并通过FAST、Harries等检测算法实现图像中的特征点检测。

（2）特征描述

特征描述主要包括特征计算和特征向量生成两部分。在特征计算过程中，RIFT 使用log-Gabor卷积结果构建最大索引图（Maximum Index Map，MIM），进而对特征进行描述。首先，计算图像在Ns个尺度的幅值响应之和Ao(x，y)。

对于图像的每个像素(xi，yj)，可以得到表示图像频域幅值响应与方向关系的No× 1 维向量，其中，Ns和No分别为滤波器的尺度和方向数量。找到该向量最大值Amax(xi，yj)所对应的方向索引ωmax，并将该值作为MIM 中(xi，yj)位置的像素值，即可得到整幅图像的MIM。

在特征向量生成阶段，对于每个特征点，选择以特征点为中心、大小为J×J的局部邻域，并使用标准差为J/2 的高斯函数对邻域像素进行加权。RIFT 算法将局部邻域划分为6 × 6 个子网格，在每个子网格中对MIM 进行统计以构建最大索引分布直方图。最后通过拼接所有子网格的直方图获得特征向量。

2.2 多视角条件下配准性能分析

由于雷达复杂的成像机制和成像方法，同一目标在不同视角的雷达图像中可能存在明显的特征差异，使得多视角雷达图像配准一直是一项富有挑战性的工作。图1中给出了不同视角下同一区域的成像结果，图中红色箭头指示了雷达照射方向。通过观察红色方框内的图像特征，可以明显看出A1、A2区域和其对应的B1、B2区域在不同视角下的特征差异，雷达从两个相对的方向分别观测到了目标的不同侧面。这类不同视角间的辐射畸变对匹配算法有很强的误导性［23］。

图1 不同视角下目标的散射特性差异Fig.1 Difference of target characteristics from different views

除此之外，由于雷达的斜视成像机制，存在高程起伏的目标还会对周围的目标产生遮挡，在图像中形成阴影区域。如图2 所示，图中红色箭头指示了雷达照射方向，由于雷达照射方向不同，同一目标会对不同区域造成遮挡，进而在图像间形成了红色方框内存在差异的阴影区域。这些特征差异会使图像配准变得更加困难。

图2 不同视角下目标的阴影差异Fig.2 Shadow difference of targets from different views

针对多视角雷达图像配准中存在的问题，通过开展RIFT算法配准实验，对其在多视角条件下的性能进行分析。

首先，在特征检测阶段，由于图像阴影区域与非阴影区域灰度差异较大，阴影边缘像素具有较大的灰度梯度，SIFT 等基于灰度梯度的配准算法会将很多阴影边缘像素检测为特征点。由于不同视角下雷达图像间的阴影区域存在差异，这些特征点在待配准图像间很难建立正确匹配，过多的错误匹配将会给后续去除离群点过程带来严重干扰，最终导致该类算法无法给出正确的图像配准结果。

RIFT 算法的特征检测结果如图3 所示。观察同一区域的最大矩图与最小矩图，阴影边缘和阴影内部像素幅值很低，其不会被检测为特征点。RIFT算法的特征计算方法对阴影边缘不敏感，能够有效避免此类不存在正确匹配的特征点对匹配造成干扰。与此同时，房屋、道路等随视角变化较小的纹理特征在最大矩图与最小矩图中拥有较高幅值，被检测为图像特征点。相较于基于灰度梯度的图像配准算法，RIFT算法能够有效地避免阴影区域的影响，对图像中的特征点进行准确检测，因此选择改进该算法以实现多视角雷达图像的配准。

图3 基于相位一致性的RIFT算法特征检测结果Fig.3 RIFT feature detection results

在特征描述阶段，由于图像中大部分相位一致性接近于零且易受噪声干扰，RIFT采用MIM对特征向量进行构建并根据特征点间MIM 的相似性进行特征匹配。但是，如图4 所示，以图像中A1与B1、A2与B2为例，同一区域在不同视角下分别表现出明显的阴影特征差异和非线性辐射畸变，使这些区域的MIM 存在巨大差异，进而会导致同一目标在两幅图像中会产生不同的特征向量，无法形成有效匹配。

图4 RIFT算法特征计算结果Fig.4 RIFT feature calculation results

综上，为了能够在不同视角的雷达图像间建立正确、稳定的匹配关系，还需要在RIFT 算法基础上进行改进，解决以下两点问题：

1）不同视角下同一目标不同的散射特性导致配准算法计算得到的图像特征不一致，进而使得同一目标在两幅图像中产生不同的特征向量，无法形成有效匹配；

2）当目标特征邻域内存在阴影区域时，不同视角雷达图像间的阴影区域差异会导致目标在两幅图像中产生不同的特征描述，进而使得同一目标在两幅图像中产生不同的特征向量，无法形成有效匹配。

3 基于多特征描述与阴影感知的改进RIFT算法

3.1 多特征描述

RIFT 算法使用图像与2D-LGF 卷积结果构建MIM，进而对特征点的特征进行描述。通过上文分析可知，在雷达图像中，同一目标在图像中的特征可能会随视角变化而改变，不同视角下同一目标的MIM 不具有相似性，利用其构建的特征向量同样存在较大差异，导致无法形成正确匹配。

根据RIFT 算法原理，MIM 基于图像滤波后的幅值响应构建，其中每个元素的值等于幅值响应序列最大值的索引。算法没有充分利用log-Gabor 滤波器实部、虚部卷积结果的全部信息以应对图像间非线性畸变，当卷积结果的实部或虚部任一响应发生变化时就会导致特征向量发生变化。当图像间非线性畸变严重时，继续使用MIM 进行特征描述会导致正确匹配点数减少甚至产生错误匹配，最终使得算法拟合得到的图像几何变换关系误差增大，图像无法准确对齐，如图5（a）、（b）所示。

针对此问题，本文提出了基于2D-LGF 卷积结果的多特征描述方法，利用偶对称log-Gabor 小波和奇对称log-Gabor 小波的空间域性质对雷达图像中两种不同特征进行提取并分别构建特征向量用于特征匹配，使单一的特征变化不再影响特征向量生成，增强算法对目标散射特性变化的鲁棒性。具体做法如下所示：

一维log-Gabor 滤波器的传递函数在频域中被定义为：

其中，ω0是滤波器的中心频率，σω是滤波器的带宽参数，一般通过逆傅里叶变换得到滤波器的空间域参数。一维奇对称log-Gabor 小波和偶对称log-Gabor 小波的空间域形状如图6（a）、（b）所示，其形状分别与图像处理中的梯度算子和拉普拉斯算子相似，在合适的尺度下能够对图像中灰度阶跃和灰度突起产生较大的响应，实现对不同特征的提取，如图6（c）、（d）所示。由于2D-LGF 可以通过一维log-Gabor 滤波器在不同角度进行高斯扩展获得［24］，二维奇对称log-Gabor 小波和偶对称log-Gabor 小波同样可以实现对图像中两种不同特征的提取。

图6 log-Gabor小波空间域性质Fig.6 Properties of log-Gabor wavelet in space domain

基于上述性质，改进RIFT算法特征向量生成方法如图7所示。

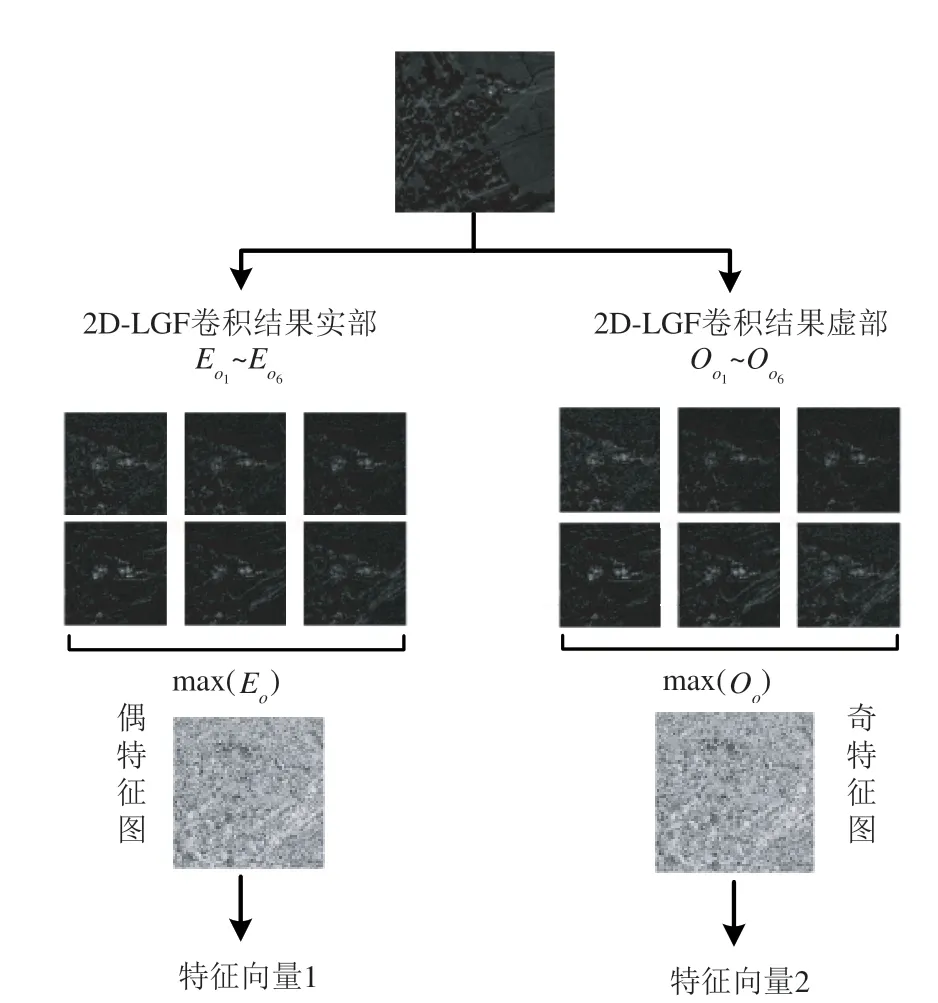
图7 改进RIFT算法特征向量生成方法Fig.7 Feature vector generation method

对于给定的图像I(x，y)，首先需要将图像与2D-LGF 进行卷积以获得奇对称log-Gabor 小波和偶对称log-Gabor 小波的响应eso(x，y)和oso(x，y)；然后在每个方向o上，分别将所有尺度得到的响应进行累加，得到实卷积序列E0(x，y)与虚卷积序列Ο0(x，y)。

最后，在两组卷积序列各像素位置(xi，yj)处找到的最大值max(E0)和max(O0)用以分别构建“奇特征图”与“偶特征图”，并在两幅特征图中生成针对不同特征的两组特征向量。

选取两张地面纹理信息丰富的不同视角雷达图像，利用本文提出的多特征描述方法对其进行匹配的结果如图8 所示。进行配准测试时，与RIFT 算法相比，除特征描述方法外其余均保持一致。从匹配结果中我们可以看到，相较于图5 中RIFT 算法的图像配准结果，本文提出的方法能够得到数量更多、更精确的匹配点集，配准后图像纹理特征能够得到更好的对齐效果，这表明多特征描述方法适用于解决多视角雷达图像问题中的非线性辐射畸变问题，对该问题拥有更高的鲁棒性。

图8 多特征描述方法多视角雷达图像配准结果Fig.8 Multi-view radar image registration results of multi-feature description

3.2 基于阴影感知的特征向量生成

除了可能变化的散射特性外，不同视角的雷达图像间还存在阴影区域的差异，这类差异同样会导致目标在两幅图像中产生不同的特征向量，使算法无法在多视角图像间建立有效的匹配关系。

在不同视角下，同一目标的特征邻域示意图如图9 所示，为了方便描述，设置子邻域数量为4 × 4，该目标在两个视角下的子邻域分别为a1～a16、b1～b16。从地面纹理信息可以明显看出两幅图像为相同区域，但是因为受到目标阴影的影响，a6，a7，a10，a11与b6，b7，b10，b11四个对应位置子邻域中的特征存在巨大差异；其他子邻域由于没有受到阴影影响，基本拥有相同的特征。如果采用RIFT 的特征向量生成方法，利用全部子邻域生成特征向量进行匹配，存在差异的子邻域将会生成不具备相似性的特征向量，进而导致出现错误匹配，影响图像的配准精度。

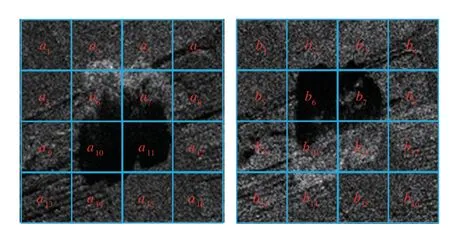
图9 不同视角下同一目标的特征邻域示意图Fig.9 Local image patch of the same object from different views

因此，为了解决阴影区域给多视角雷达图像配准带来的问题，本文提出了基于阴影感知的特征向量生成方法，通过图像阴影检测的方法标记阴影像素，并为受阴影影响严重子邻域生成的特征向量施加掩膜，保留其他子邻域生成的特征向量进行后续匹配。具体流程如下所示。

首先，对图像中的阴影区域进行检测。由于阴影区域灰度很低，经高斯滤波后，存在阴影的雷达图像的像素灰度分布曲线相较于无阴影图像在低灰度区存在明显失真［25］。受该思路的启发，我们在研究中发现：当雷达图像中存在阴影时，经2D-LGF滤波得到幅值分量序列Ao(x，y)（归一化至[0，128]）同样会在低灰度区存在失真现象，如图10所示。

图10 不同雷达图像的幅值分量分布Fig.10 Amplitude component distribution of different radar images

其中，失真是指滤波得到的幅值分量分布曲线中某一区域的形状不符合整体变化趋势。在曲线的失真区域，对应幅值分量大小的像素数量几乎停止增加甚至减少。也就是说，在失真区域幅值分量分布曲线的梯度会出现连续接近零或为负的现象。基于幅值分量分布曲线的梯度可以确认曲线是否存在失真区域，进而估计阴影区域灰度大小，实现雷达图像的阴影区域检测。

设雷达图像幅值分量最小值为amin，当Ao(xi，yj)=k时对应的像素数量为Q(k)，Q取最大值时对应的幅值分量为amax。由于阴影区域灰度值较小，失真区域一定位于曲线左半部分，因此只对[amin，amax]内的曲线梯度进行分析。与此同时，分布曲线的起始和峰值区域梯度也很小，会对曲线失真判断造成干扰，在检测前需要将这两个区域排除。设置起始区域和峰值区域的边界长度为Nb，最终需要进行分析的区域为[amin+Nb，amax-Nb]。综上，曲线的梯度为：

设曲线左半边的平均梯度为Gradm，寻找曲线中梯度小于Gradm/2 所有幅值分量，如果曲线中存在连续Nd个幅值分量对应的梯度均小于Gradm/2，则认为此区域为失真区域，并将该区域梯度分量平均值的m倍作为阈值对阴影进行检测。

实现图像中阴影区域检测后，还需要在此基础上消除阴影区域对特征向量的影响。在特征向量生成过程中，首先，以特征点为中心选择大小为J×J的邻域并将其分成6 × 6 个子邻域（每个邻域边长为J/6），并在每个子邻域中统计各方向的奇、偶特征图用于生成初始特征向量Ve0，Vo0，特征向量长度为6 × 6 ×No=36No。然后，统计各子邻域中的阴影像素数量Nsh对子邻域进行有效性检测。当Nsh＞(J/6)2×Tn，即阴影像素数量占子邻域总像素数量比例大于Tn时，认为该子邻域中的特征受阴影影响严重，其在两幅图像间可能存在较大差异，特征向量中由该子邻域生成的部分不应参与后续匹配过程，其中Tn为子邻域无效阈值。因此，为阻止特征向量中的无效部分参与特征匹配，需要在特征向量中为其添加“掩膜”。设掩膜向量为Vmask

Vmask长度与特征向量长度相等。v1，v2，v3，…，v36均为长度为No的向量，其在Vmask中的位置分别对应36 个子邻域所生成的特征向量在初始特征向量中的位置。当第n个子邻域阴影像素数量过多被检测为无效子邻域时，将vn设置为全0向量，否则为全1向量。改进RIFT算法输出的特征向量为

其中，⊙表示哈达玛积，即两向量对应元素相乘。配准算法在特征匹配时一般利用特征向量的欧氏距离建立初始的匹配关系，在此过程中，需要计算特征点到另一幅图像中所有特征点的欧式距离并进行比较。但是由于阴影区域的差异性，算法输出的特征向量无效部分可能并不重叠。如果直接对欧氏距离进行计算，两个特征向量将会出现一个特征向量中某部分被掩膜向量置零，而另一个特征向量对应部分未被掩膜向量置零的情况，进而导致欧式距离计算结果不正确。因此，对于将要计算欧氏距离两个特征向量，需要对其无效区域取并集共同施加掩膜再进行匹配，即

示意图如图11所示。需要注意的是，当特征向量中被掩膜覆盖的元素占总元素比例大于TV时，该特征向量的匹配结果并不稳定，需要将这类匹配点对删除。最后，将特征向量归一化，使不同特征点间的欧氏距离能够直接进行比较。除此之外，阴影区域是由存在高程起伏的目标产生的，这类目标可能还会存在小幅度的几何畸变，可以采用适当扩展掩膜面积的方式防止其对匹配可能造成的干扰。

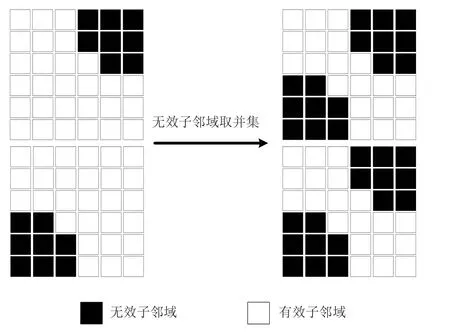
图11 阴影感知匹配示意图Fig.11 Sketch Map of shadow perception matching

选择一组阴影面积较大的不同视角雷达图像，利用本文提出的多特征描述方法，比较采用阴影感知特征向量生成方法前后的多角度雷达图像配准效果。在配准测试时，除了特征向量生成方法不同外，其余均保持一致。原始图像与图像阴影检测结果如图12所示。对比原始图像与阴影检测结果，图像中的绝大部分阴影区域得到了有效检测。由于雷达图像相干斑噪声的影响，一些像素的灰度与阴影像素灰度近似，导致阴影检测结果中出现了小面积虚警（几个像素大小）。但是，由于算法通过阴影像素数量与子邻域像素数量的比值决定是否需要为特征向量施加掩膜，这类小面积虚警不会干扰特征向量生成结果。

采用阴影感知特征向量生成方法前后的多角度雷达图像特征匹配结果如图13 所示。由于图像阴影区域的影响，不对阴影处理直接进行匹配时，如图13（a）所示，红框内的三对特征点发生了明显的错误匹配，这些错误匹配导致配准算法输出的图像间几何变换关系误差增大，最终使图像无法正确对齐。利用本文提出方法对阴影进行处理后，虽然算法在匹配点数量上改变并不明显，但在配准准确性上明显优于传统算法，在图像中并没有出现明显的错误匹配，图像的纹理细节也得到了正确的对齐，如图13（b）所示。

图13 采用阴影感知特征向量生成方法前后图像配准结果Fig.13 Image registration results before and after shadow perception

利用本文3.1、3.2节提出的配准方法后，图1、图2 中的图像配准结果如图14 所示。通过观察配准后的棋盘图，图像纹理细节能够得到良好的对齐效果。图1、图2 所列出的两种情况的图像配准问题得到了有效解决。

图14 本文方法多视角雷达图像配准结果Fig.14 Multi-view radar image registration results of proposed method

4 多视角雷达图像配准实验

为了验证改进RIFT 算法对多视角雷达图像配准问题的有效性，实验选取了多组不同视角且拥有丰富地表附属物区域的雷达图像进行配准，对结果进行定量评估并与三种先进的算法进行了比较。为了保证实验的公平性，所有匹配方法均采用最近邻距离比［26］（Nearest Neighbor distance ratio，NNDR）方法为基础选取初始匹配点，使用快速样本共识［27］（Fast sample consensus，FSC）方法进行离群点剔除得到最终的匹配结果。

4.1 数据说明与评价指标

本文选取了中国四川地区的机载SAR 图像开展配准实验，成像数据获取视角示意图如图15 所示，分别在三条航线上对同一区域进行正侧视成像（图中箭头方向表示飞机飞行方向）。实验利用本文提出的算法对数据中四组具有典型性的不同视角图像进行配准，所选四组图像如图16 所示，具体参数如表1 所示。实验所选区域中包含了大量房屋、树木等地表附属物，这类地表附属物在不同视角图像中存在明显的特征差异和阴影差异，给图像配准带来巨大困难。

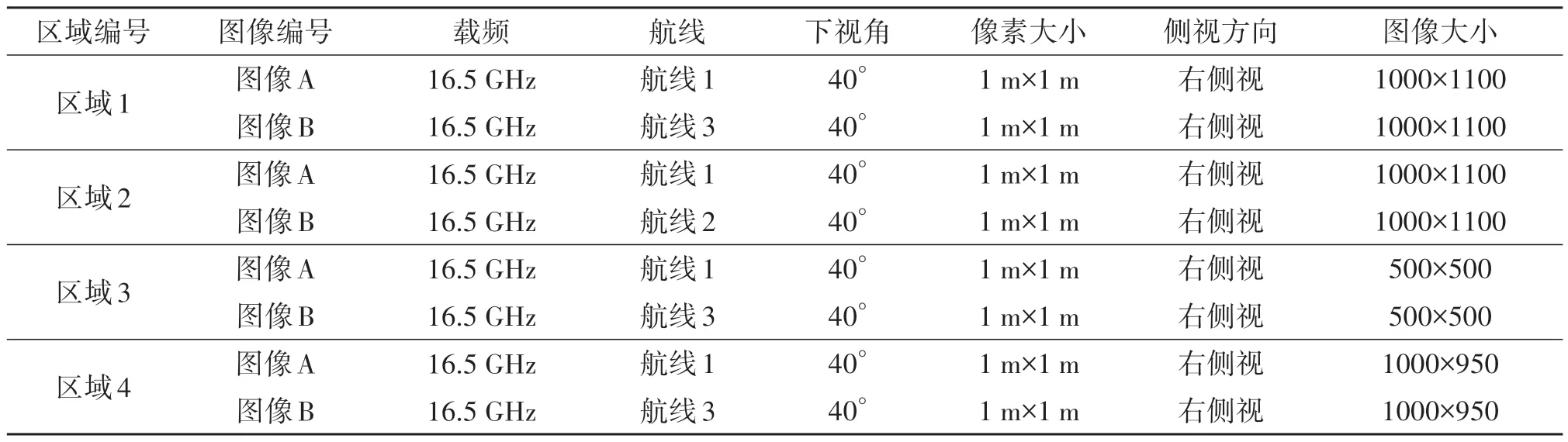
表1 本文使用的SAR图像参数Tab.1 SAR image parameters used in this paper

图15 数据获取视角示意图Fig.15 Views of data acquisition

图16 配准实验数据Fig.16 Data of registration experiment

本文使用均方根误差、正确匹配概率和正确匹配点数量作为评价指标。

1）均方根误差：实验采用仿射变换模型拟合待配准图像间的几何变换关系。对于每组图像，我们挑选3 组特征明显的对应关系，并使用这些对应关系在配准后几何位置的均方根误差来评估配准算法的精度；

2）成功匹配概率：实验采用FSC 方法对初始匹配点集进行离群点剔除，由于该方法具有随机性，为了保证实验结果的说服力，每组匹配图像执行20次匹配，成功匹配次数占总匹配次数的比例即为成功匹配概率；

3）正确匹配点数量：经过NNDR 建立初始匹配关系，并经过FSC 进行离群点剔除后剩余的匹配点对数量。

实验中，认为配准得到的均方根误差小于10时图像得到成功匹配。

4.2 参数优化

本文在RIFT 算法的基础上对其特征检测与特征描述方法进行了改进，所使用的参数中子邻域边长J、2D-LGF 方向数No、尺度数Ns沿用RIFT 算法中的设定，即J=96、No=6、Ns=4，不再对参数调整进行实验分析。除此之外，本文使用的主要参数包括：阴影检测参数Nb、Nd、m和特征向量生成参数Tn、TV。

阴影检测参数中：Nb为阴影检测中的边界区域长度，检测前需要将分布曲线两侧长度为Nb的区域去除，防止分布曲线起始和峰值区域对曲线失真判断造成干扰。通常，Nb越大防止干扰的性能越好，但设置过大会导致失真区域被错误去除。Nd为失真区域长度，当图像幅值分布曲线的梯度中连续Nd个幅值上的梯度小于一定值时，则认为该区域为失真区域。Nd过小时，局部异常值会被错误检测为失真区域；Nd过大时，由于图像失真区域长度有限，算法无法对阴影实现有效检测。m为阴影检测阈值系数，阴影检测时，将失真区域对应滤波幅值平均值的m倍作为检测阈值，m设值过小会导致阴影检测存在漏检，反之则会导致阴影检测发生虚警。为了实现阴影的准确检测，进而完成图像的精确配准，本文以区域3 的雷达图像作为待检测图像，设计了三个独立实验以调整变量至最优值。其中每个实验只有一个参数作为变量，其他参数为固定值，具体参数设置如表2 所示。对与每个参数，使用阴影检测结果与真是阴影区域的相似性作为评价指标，实验结果如图17所示。

表2 阴影检测参数设定实验预设Tab.2 The details of parameter settings

图17 阴影检测参数设定实验结果Fig.17 Experimental results of shadow detection parameter setting

从实验结果可以看出，当Nb=3、Nd=3、m=1.4时，算法的阴影检测结果最接近雷达图像中真实的阴影区域，取得最优的检测结果。而参数取其他值时，阴影检测均会出现一定程度的虚警和漏检现象，因此将阴影检测参数设置为：Nb=3、Nd=3、m=1.4。

特征向量生成参数中，Tn为子邻域无效阈值，用于判断子邻域所生成的特征向量是否需要添加“掩膜”。Tn设置过高会导致受阴影影响较小的子邻域中的特征被忽略，特征向量包含的特征信息减少；相反则会使算法无法有效消除不同视角图像间阴影差异的影响。参数TV用于判断施加掩膜后，剩余的特征向量长度是否可以实现特征的稳定匹配。TV越大则算法所保留的特征点的特征向量有效长度越长，其中包含的特征信息越多，匹配结果越稳定；但与此同时，图像中受阴影影响较小的特征点不再参与匹配，图像间部分正确匹配被剔除。因此，合适的特征向量生成参数同样重要。本文以4.1 节中选取的四组图像作为待配准图像，设计了两个独立实验以调整变量至最优值。其中每个实验只有一个参数作为变量，其他参数为固定值，具体参数设置如表3 所示。对于每个参数，将图像执行十次配准，使用平均匹配点数量和正确匹配概率作为评价指标，实验结果如表4、表5所示。

表3 特征向量生成参数设定实验预设Tab.3 The details of parameter settings

表4 Tn设定实验结果Tab.4 Experimental results of Tn

表5 TV设定实验结果Tab.5 Experimental results of TV

从表4、表5 显示的实验结果中可以看出，当Tn=0.5、TV=0.4 时，本文所提算法在匹配点数量和正确匹配概率两项性能上达到最优。因此，在性能分析实验中，将特征向量生成参数固定为Tn=0.5、TV=0.4。

4.3 实验结果

本文采用的对比算法分别为SIFT［11］、SARSIFT［6］、RIFT［17］。其中，SIFT 是经典的光学图像配准算法，SAR-SIFT 专用于合成孔径雷达图像配准，RIFT是用于多模态图像的配准方法，实验前已将各算法参数调整至最优。多种算法的特征点匹配结果如图18 所示。表6、表7 分别给出了算法在多视角雷达图像配准性能指标。

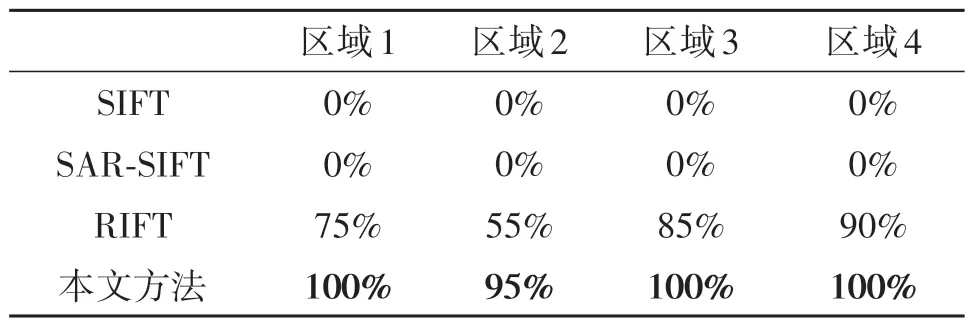
表6 不同配准算法的成功匹配概率Tab.6 Successful matching probability of different algorithms

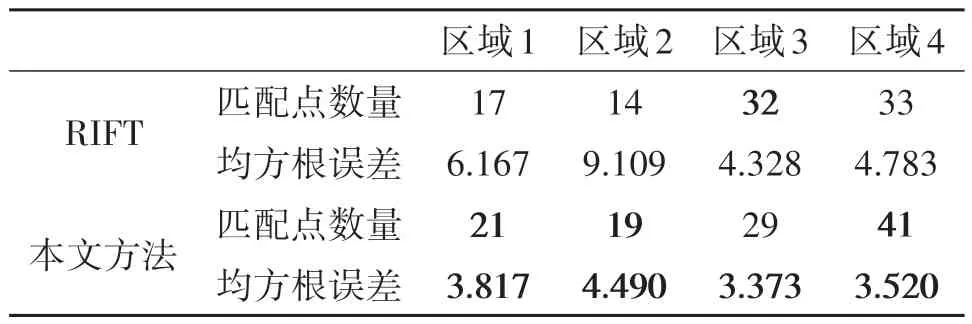
表7 不同配准算法配准性能对比Tab.7 Comparison of registration performance of different algorithms

图18 不同配准方法的特征匹配结果对比，从左至右分别为区域1～区域4Fig.18 Comparison of feature matching results of different methods，from left to right are area 1 to area 4

接下来对个图像间的配准结果进行具体分析。区域1 为城镇区域图像对，两幅图像分别从相对的照射方向上得到，由于区域中丰富的地表附属物，其导致图像间存在明显的非线性辐射畸变和阴影差异。基于梯度的SIFT、SAR-SIFT算法无法有效提取图像中的特征点，同样无法准确提取图像中的相似特征生成特征向量，最终得到错误的匹配结果。基于相位一致性的RIFT 算法在75%的成功匹配概率下，平均每次成功匹配得到17 对匹配点；而本文方法在100%的成功匹配概率下，平均每次匹配得到21 对匹配点，相较于RIFT 取得了更好的特征匹配结果。

区域2 与区域1 所选区域相同，但不同的是，区域2 两幅图像分别从垂直的照射方向上得到，相较于区域1，区域2 图像间存在着更明显的非线性辐射畸变。在其影响下，SIFT、SAR-SIFT 算法同样无法得到正确的匹配结果；RIFT算法的成功匹配概率下降到55%；而本文方法依旧能够以95%的成功匹配概率稳定输出正确的图像配准结果，在其他性能指标上也优于现有算法。

区域3 与区域4 为村庄区域图像对，区域中大量如树木、土堆等地表附属物，雷达图像中纹理特征与阴影多由这些物体产生，这类目标在不同视角间非线性辐射畸变较小，但存在明显的阴影差异。从匹配结果中可以看出，SIFT、SAR-SIFT 仍然无法对图像进行正确匹配；RIFT算法的各项性能指标与区域1、区域2 结果相比有明显提高，由于辐射畸变较小，利用MIM 特征描述方法也能够在图像间获得一定数量的匹配点对，在进行区域3 匹配时其得到的正确匹配点数甚至略高于本文提出算法。但是在阴影区域的影响下，RIFT 算法配准结果并不稳定，存在10%～15%错误匹配概率而且配准误差较大，本文提出方法在成功匹配概率和均方根误差两个指标上均存在显著优势。

利用本文方法进行图像配准得到的棋盘图如图19所示，从图中可以看出不同区域的图像在细节处拼接整齐，图像拥有较高的配准精度。

图19 本文方法图像配准得到的棋盘图Fig.19 Checkerboard mosaic map of our method

在本文选取的四组数据中，由于图像间雷达视线方向接近垂直或相对，雷达发射的电磁波会照射在目标完全不同的侧面，相较于其他视角关系，图像间将表现出更为明显的差异。利用这组数据能够更好的说明本文算法在多视角雷达图像配准中的有效性。与此同时，所选区域中的地表附属物的高度相较于地面变化较小，不会在多视角雷达图像间表现出显著的几何畸变，进而在实验中可以忽略几何畸变对配准产生的影响。结合实验结果可以看出，针对存在丰富地表附属物的城镇、村庄等区域，本文所提出的方法能够在多视角条件下实现SIFT 与SAR-SIFT 无法完成的雷达图像配准功能；除此之外，与性能最好的RIFT 算法相比，其成功匹配概率平均提高29.5%，正确匹配点数量平均提升14.6%，并且配准均方根误差可降低36.2%。本文方法可在保证高可靠性与高精度的前提下实现存在丰富地表附属物区域的多视角雷达图像配准。

5 结论

为了提高算法对非线性辐射畸变和阴影区域差异的鲁棒性，实现存在丰富地表附属物区域的多视角雷达图像配准，本文分析并总结了现有算法在多视角雷达图像配准中的存在的问题，并在此基础上提出了一种基于多特征描述和阴影感知的改进RIFT 图像配准算法。首先，算法利用log-Gabor 滤波器实部和虚部的空间域性质对雷达图像中两种不同特征进行提取并分别构建特征向量用于特征匹配，使单一的特征变化不再影响特征描述，增强算法对非线性辐射畸变的鲁棒性。其次，在特征向量生成过程中，利用log-Gabor 滤波器对阴影区域响应低的性质，实现对图像阴影区域的检测，并为受阴影影响严重子邻域生成的特征向量施加掩膜，保留图像中的相似特征进行后续匹配。实验表明，该方法能够在多视角雷达图像间建立稳定、准确的匹配关系，性能明显优于现有算法。