风光火打捆系统暂态稳定性及其虚拟同步机策略研究

余明昊， 顾雪平， 李少岩

(华北电力大学 电气与电子工程学院，河北 保定 071003)

0 引 言

随着国内外对于各类化石能源的消耗不断加剧及自然环境的恶化,减少对传统火电的依赖性是必然的趋势。而风电、光伏等新能源发电形式具有无污染、资源丰富等优势。在我国,风电、光伏等新能源的建设分布与我国的用电需求在空间分布上有逆向趋势。我国主要的风电大多分布在西北地区,同时光伏发电也大多处于光照资源丰富但消纳电能能力不足的西北地区,而我国的主要电能需求则在华中以及沿海经济发达地带。所以,将电能外送便成为了解决新能源发电、用电不平衡问题的首选方法。

以风光火打捆交直流混联外送系统为基础,将电能送至电能消纳能力强、需求高的地区能高效地缓解电力的不平衡消纳情况。但风电、光伏等新能源的高比例并网会导致电力系统的整体暂态稳定性更加复杂和难以预测,同时会引起系统送端惯量和系统暂态稳定裕度的下降[1,2]。目前,以虚拟同步机策略作为改善新能源高比例并网引起的送端惯量问题的方法虽已被广泛接受,但还未有研究将虚拟同步机策略与风光火打捆外送系统相结合。因此,需要对典型风光火打捆交直流混联外送系统的暂态稳定性及其惯量提升问题进行深入的研究。

目前针对风光火打捆或风火打捆系统的暂态稳定性方面已进行了一定地研究。文献[3-6]从理论和仿真等方面分析了多种不同指标对风火打捆外送系统的暂态稳定性的影响机制,并提出了控制算法方面的改进。文献[7]针对风光火打捆系统,分析了火电配比及多种直流运行故障对系统的影响机理,并讨论了风电、光伏的故障脱网时序。文献[8]针对风火打捆系统中的双馈风电机组,给出了其等效外特性,并仿真分析了其暂态特性以及故障穿越时风机的故障响应。而针对风电、光伏机组的VSG策略,文献[9-11]首先从基础原理、实现方法和控制目的等方面介绍了应用于风电和光伏的VSG控制策略的相关概念,总结了VSG控制策略的研究现状。文献[12]以双馈风电机组参与有功调频后稳定运行为目标,提出了一种以风速和频率偏差值为参考的虚拟同步机参数自适应控制。文献[13]将风火打捆系统与VSG策略相结合,分析了电网故障和风速扰动下VSG策略的有效性,但并未在送端计及光伏机组并入的影响。总体上看,针对风光火三者打捆系统的各方面研究以及结合虚拟同步机策略的送端惯量提升问题的研究依然较为初步,需要更进一步的探索。

本文基于PSCAD仿真软件,首先搭建了风电、光伏、火电打捆外送系统的基础仿真模型,包括送端的双馈风电机组、光伏、火电机组部分的模型以及高压直流模型等。选取火电机组功角首摆角度和功角波动恢复情况为指标来表征打捆系统的暂态稳定性。之后通过仿真分析了不同的交流故障类型、送端风光火三者占比以及直流整流侧控制方式对打捆系统暂态稳定性的影响,并给出了相应结论。之后在双馈风电机组和光伏的换流器环节中引入虚拟同步机控制策略,并通过仿真验证了该控制策略对送端打捆系统惯量的有效提升,旨在为风光火打捆交直流混联电网送端系统的建设与高效运行提供帮助和参考。

1 风光火打捆交直流混联系统建模

1.1 光伏系统模型

光伏发电系统主要由光伏电池阵列模块、并网换流器及其内部控制模块组成。

依据光伏电池的内部参数,经过化简便能得出可用于工程计算的光伏电池组的模型表达式[14,15]。

(1)

式(1)中:Isc、Im分别为短路电流和最大功率点的负载电流;Uoc、Um则分别为开路电压和最大功率点的负载电压。

在d-q-0坐标系下,光伏机组换流器的机电暂态等效方程为

(2)

式(2)中:Ed、Eq、id、iq为换流器交流电压和交流电流的d、q分量;L为连接电抗;f为系统频率;Ud、Uq为电网侧电压的d、q分量;R为连接电阻;s为微分算子。

1.2 双馈风电机组模型

本文以双馈风电机组作为风光火打捆系统送端风电部分的仿真模型对象。DFIG相对异步风力发电机和直驱式交流永磁同步发电机等类型的风机具有风能转换效率高、可靠性高、调度灵活、经济性好等一系列优点。

DFIG仿真模型的主体部分主要由风轮机、发电机、换流器模块以及电气控制、轴系传动模块等部分组成,如图1所示。

双馈风电机组的运动过程可以使用电压、磁链等方程组来表示。双馈风机的电压方程组分为定、转子电压方程两个部分:

(3)

双馈风力机组的定、转子磁链方程为

(4)

转矩运动方程为

(5)

式(3)、(4)、(5)中,ud1、ud2、uq1、uq2分别为机组定、转子侧电压的d、q轴分量;id1、id2、iq1、iq2分别为机组定、转子侧电流的d、q轴分量;ψd1、ψd2、ψq1、ψq2分别为定、转子磁链的d、q轴分量;np为发电机的极对数;T1、T2分别为电机的拖动转矩和电磁转矩;ω、ωs分别为转子机械角速度和d-q坐标下相对于转子的角速度;L1、L2、…、Ln分别为d-q坐标下定、转子的自、互感;J1则为机组转动惯量。

1.3 直流输电系统模型

本研究中,直流系统的仿真模型主要由线路模块、控制模块以及其他附加控制模块组成。直流换流站以准稳态模型运行,对其自身的暂态过程加以忽略,直流换相过程用代数方程的方式描述,直流线路模型以T型等值电路表示[16]。

高压直流输电部分的数学等效模型:

(6)

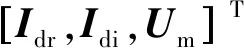
2 虚拟同步机控制部分建模

由于风电、光伏等新能源旋转备用容量小、与电网解耦运行等特点,过高的新能源占比会引起打捆外送系统送端的低惯量、低阻尼等问题,使得系统更易受故障或功率波动的影响,最终可能导致系统在大扰动下失稳。而将虚拟同步机控制策略引入打捆系统送端风电、光伏机组的并网换流器中可以有效改善送端系统的低惯量及欠阻尼问题。

VSG技术指将传统同步发电机机电暂态方程嵌入风电或光伏机组外送电力电子变换器控制策略中,使其模拟同步电机电磁与机械运动外特性[17]。

为避免建模过于复杂同时兼顾实用性,本文以二阶同步电机模型为仿真建模目标。VSG控制模拟的同步电机二阶转子运动方程可以表达为

(7)

式(7)中:Tm和Te分别表示原动机机械和电磁转矩;θ1表示功角;ω和ωref分别表示转子角速度和额定角速度;J参数为转子的转动惯量系数;D参数为转子的阻尼系数。

而定子电气方程可以表示为

(8)

式(8)中:uabc为定子侧感应电动势;eabc为定子侧三相输出端电压;Ls、Cs分别为电枢电感和电容。

采用以上两式建模,建模过程相对简便,同时也能保证逆变器具备所模拟的同步电机的惯量特性。

VSG的基本结构主要包括主电路和控制电路等几部分,其中主电路部分主要包括并网换流器以及LC滤波电路等。VSG的总体控制结构如图2所示。

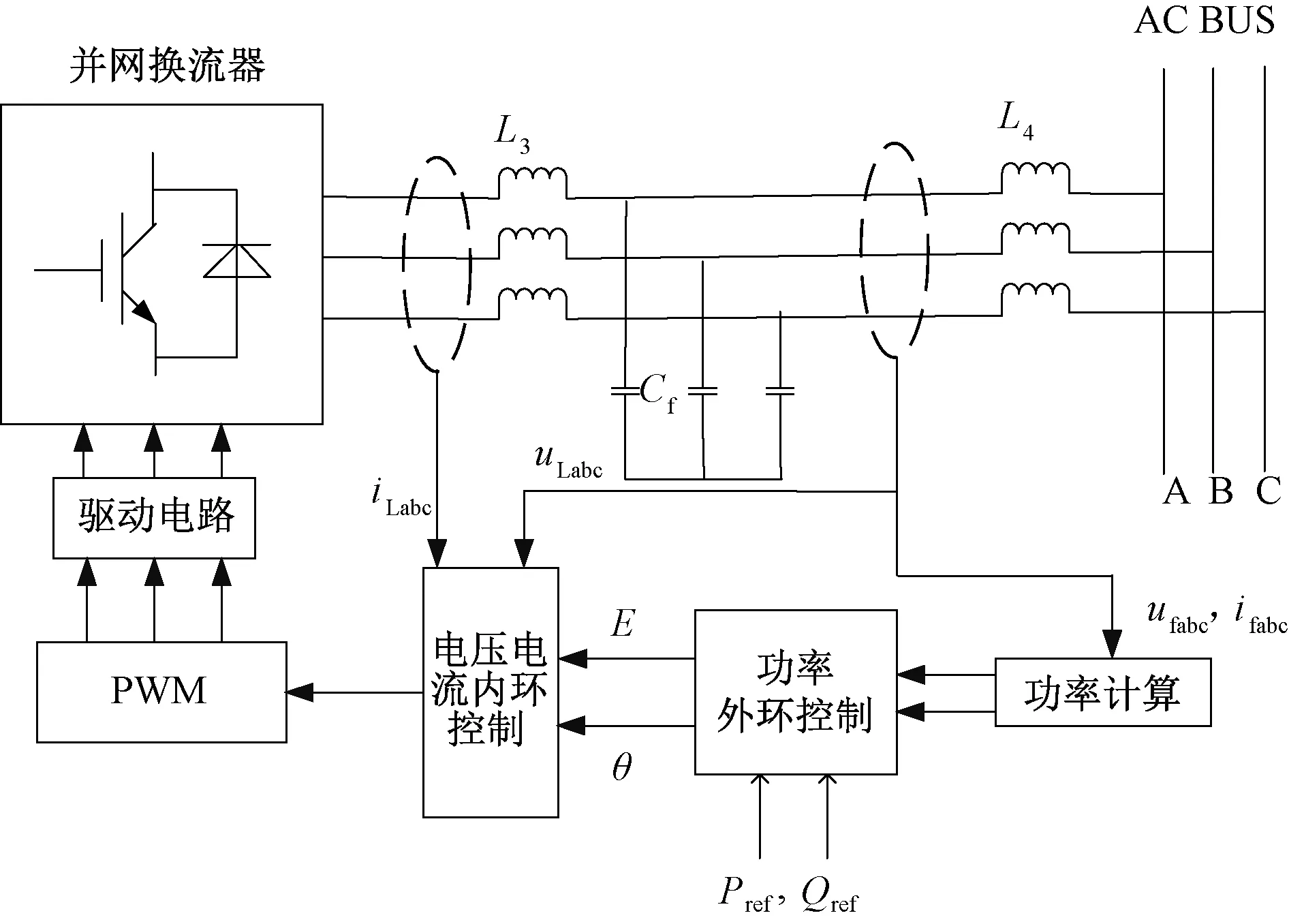
图2 VSG总体控制结构图

VSG控制算法主要在于功率外环控制部分中的有功-频率下垂控制环(P-f)和无功-电压下垂控制环(Q-E)两个部分。

VSG有功-频率、无功-电压下垂控制方程可以表示为

(9)

式(9)中:ω0、ωn分别为电网同步角速度和模拟机械角速度;Kp、Kq分别为有功-频率下垂系数、无功-电压下垂系数;Pout、Qout分别为功率计算部分得出的电网实时有功、无功。

VSG的核心计算部分是结合式(7)与式(9),通过功率给定值Pref、Qref与功率计算部分得出的传递功率Pout、Qout,经过控制环的内部计算得出虚拟内电势幅值E与相位角θ。VSG的功率控制环结构图如图3。

图3 VSG功率控制环结构图

3 打捆系统暂态稳定性仿真分析

3.1 仿真系统

本文基于PSCAD仿真平台搭建了风光火打捆外送系统的基础仿真模型。送端由双馈风电模块、光伏发电模块、火电机组模块构成,经由交、直流外送线路联接至两受端系统,如图4所示。

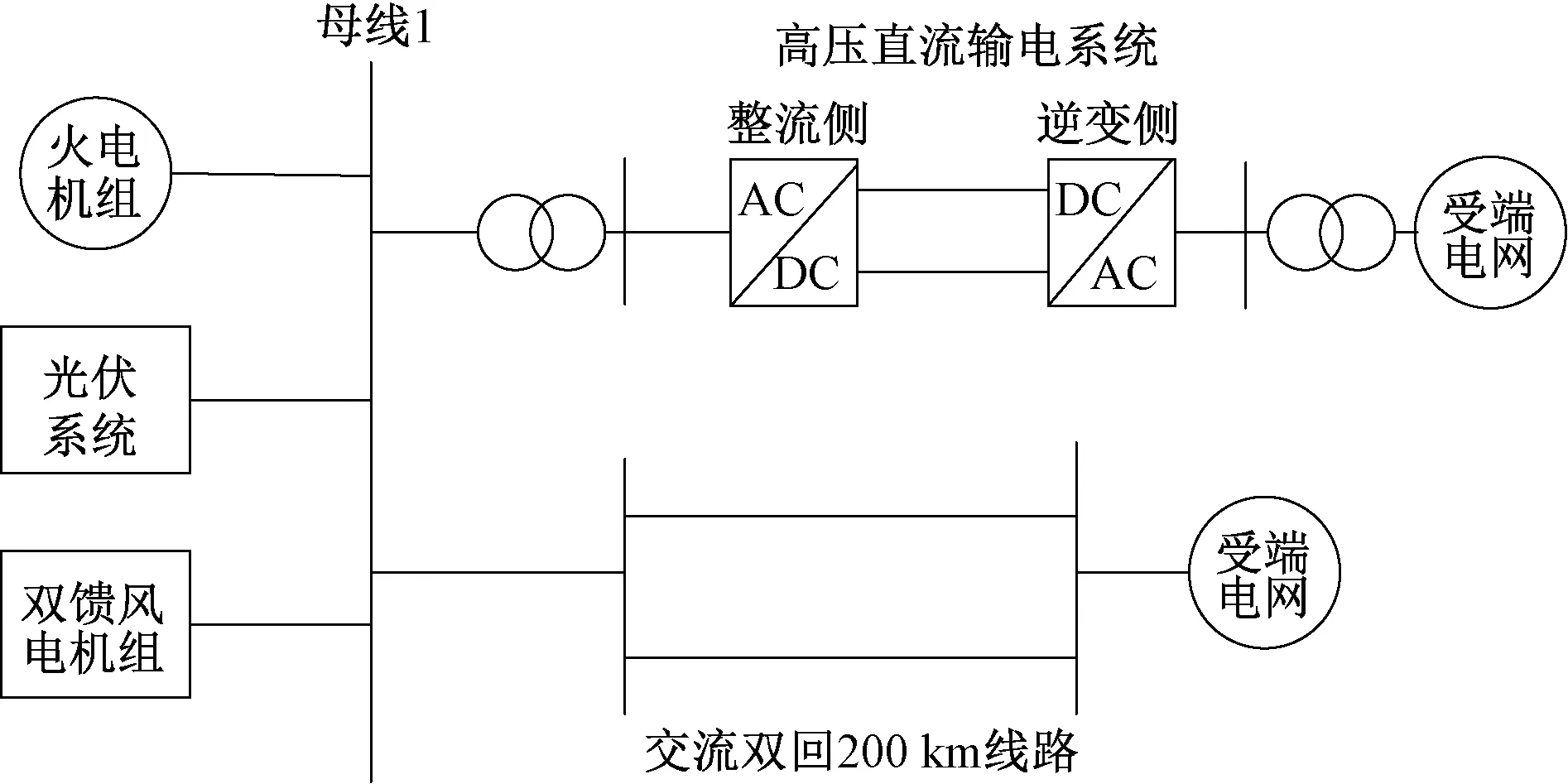
图4 风-光-火打捆外送系统拓扑结构示意图

风电机组的风速输入初始为11 m/s,输入光伏电池组的光照强度初始为1 000 W/m2,温度为25℃。汇流母线1基准电压为500 kV,双馈风电机组通过33/0.4/0.4 kV、33/500 kV变压器汇入母线,光伏发电系统通过33/0.4 kV、33/500 kV变压器汇入母线。HVDC部分电压等级为±500 kV,输送线路长度为500 km,额定换流器容量为500 MVA。交流线路由电压等级500 kV的双回输电线路组成,线路长度为200 km。

3.2 仿真分析

针对打捆外送系统,文献[18-21]基于EEAC法从理论方面分析了新能源占比对打捆外送系统暂态稳定性的影响:若维持送端总输出功率一定,当受端系统为无穷大系统时,即受端系统的惯量与容量均远大于送端系统时,新能源占比的提升会使系统暂态稳定性得到改善;而当受端系统为非无穷大系统时,系统暂态稳定性会随新能源占比的增加先提升后下降,此时即存在一个最优风光火配比可使系统暂态稳定性最优。

本仿真中两受端系统均为非无穷大系统。对风电、光伏、火电的出力情况进行分组,情况如表1所示。

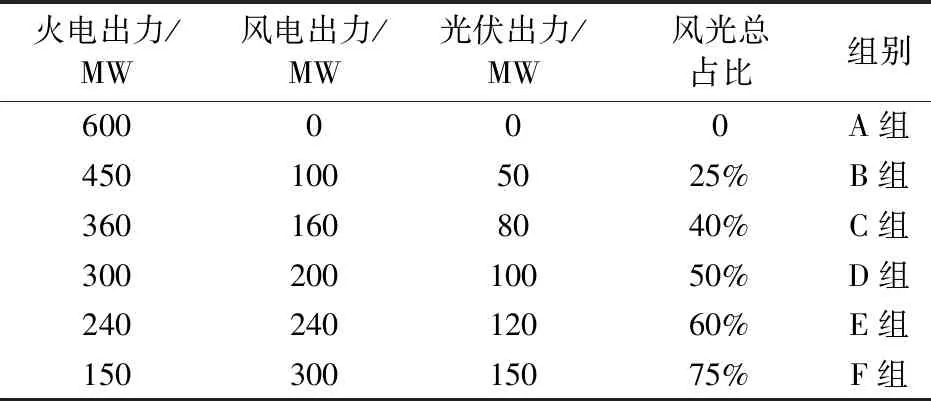
表1 风光火配比分组情况

保持送端总出力600 MW不变,首先在不考虑虚拟同步机策略的情况下仿真不同的故障类型对系统暂态稳定性的影响。选取火电机组功角首摆角度和故障恢复后功角波动的恢复情况作为判据。功角首摆越小,故障恢复后功角波动恢复的越快,系统暂态稳定性越好。

在C组配比工况下,分别设置单相接地和三相接地故障发生在交流同一回线路50%处,故障发生在2.5秒,持续0.1秒后故障清除。火电机组的功角仿真曲线如图5所示。

如图5所示,当打捆系统发生三相故障时,火电机组功角首摆角度高于单相故障的功角首摆角度,且故障恢复后功角波动的恢复情况也差于单相故障,恢复周期更长,由此可知相比于单相故障,三相故障对系统暂态稳定性的造成影响更大。三相故障是对系统危害最大的故障类型,所以后续其他工况的仿真中都将以三相故障作为研究对象。

之后分析风电、光伏、火电三者的占比对打捆系统暂态稳定性的影响。当风光的总出力占比为0、25%、50%、75%时(A、B、D、F组),设置三相故障发生在交流某一回线路50%处,故障发生在3秒,持续0.1秒后故障清除,火电机组功角波动如图6所示。

图6 风光占比对火电机组功角的影响

由图6可以看出,故障发生后,A组配比的功角首摆最大,B组其次,D组最小。故障恢复后,功角波动的恢复速度同样随着风光占比的增加而提升,但当风光占比达到75%(F组)时,系统发生故障后波动失稳。

可知,随着风电、光伏的占比在打捆系统中增加,系统的功角首摆特性和故障恢复后的功角波动情况都有所改善,但随着风光总占比的进一步增加,系统暂态稳定性会转而呈现出下降趋势,所以在本系统中存在一个最优的风光占比。

为进一步验证该结论,通过仿真求得了不同风光火占比情况下火电机组功角极限切除时间,如表2所示。

表2 不同风光火占比下火电机组功角极限切除时间

由表2可知,D组配比对应的火电机组功角极限切除时间最长,这也验证了系统暂态稳定性随风光占比的增加呈现出先提升后下降趋势的结论。

为确定本系统中的风光火最优配比,对风光占比为40%、50%、60%(C、D、E组)进行仿真分析。

由图7可知,C组仿真的功角首摆和波动恢复情况均略好于D组配比,而E组仿真中系统失稳。

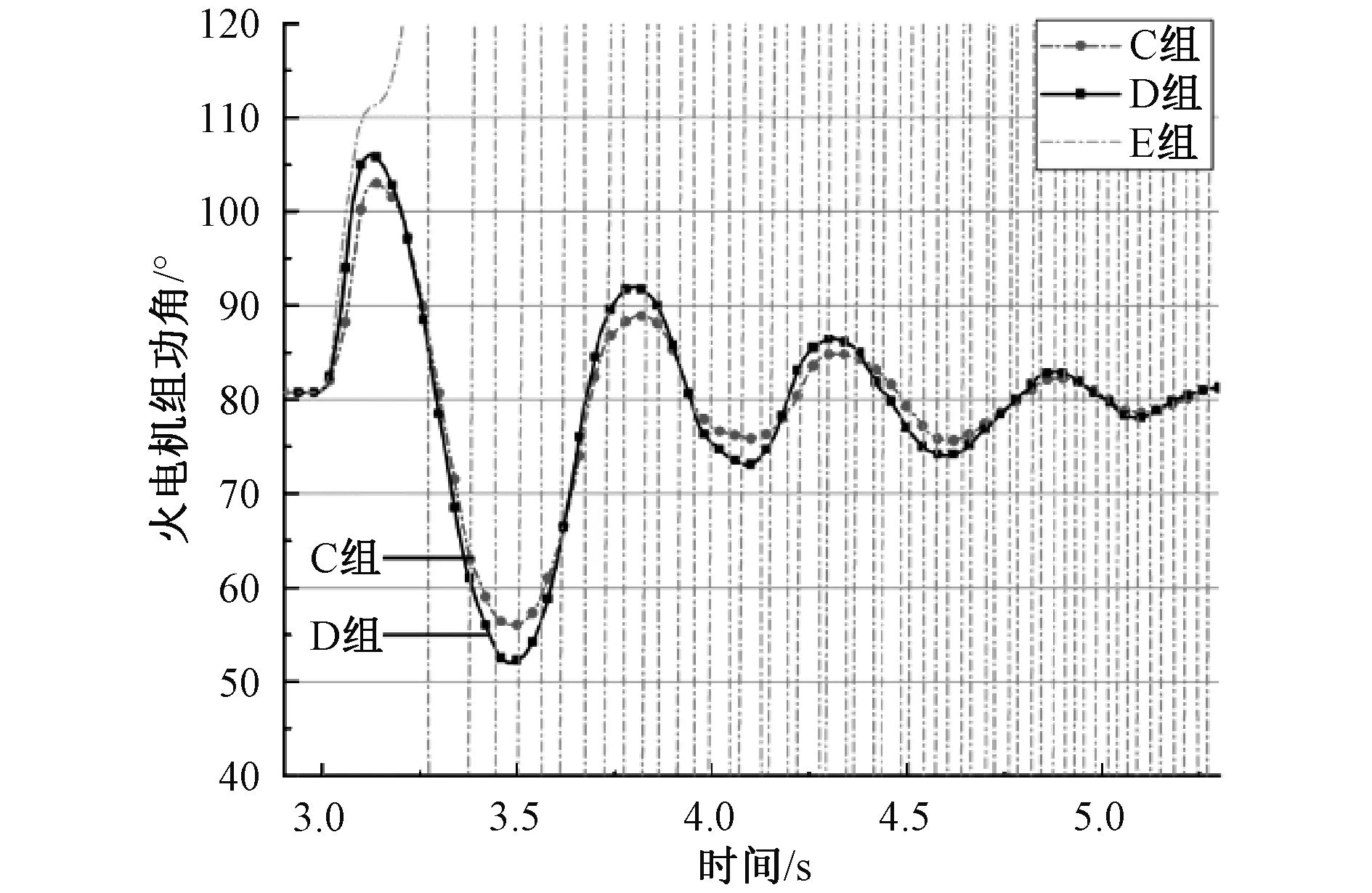
图7 不同风光火配比下功角情况

由表3可知,C组配比极限切除时间最长,而当风光配比继续上升时,火电机组的极限切除时间在呈现下降趋势。综上数据,本模型中对应的最优风光占比应该在40%左右。

表3 不同风光火占比下火电机组功角极限切除时间

实际当中,不同打捆系统的新能源最优配比受系统参数设置、模型拓扑结构等各种因素的影响而有所不同,应通过更加具体的仿真加以确定。

3.3 直流线路控制方式对系统暂态稳定性的影响

HVDC系统的整流侧有多种控制方式,不同的控制方式会对系统产生截然不同的影响。

依旧以图4系统C组数据为仿真对象,设置三相故障发生仿真3秒时交流一回线路50%处,故障持续0.1秒后清除。仿真分析HVDC系统整流侧分别以定功率和定电流方式运行时的暂态稳定性。

由图8可以看到,定功率控制方式下,打捆系统出现失稳。可知,HVDC系统整流侧采取定电流方式时系统的暂态稳定性优于定功率方式。

图8 不同直流控制方式下功角情况

若HVDC系统整流侧采用定电流控制方式,系统优先保证电流恒定,则直流电压会伴随换流母线电压因扰动产生的下降而减小。此时HVDC系统的输电功率和吸收的无功功率均会下降,降低了对交流系统支撑能力的需求;若HVDC系统整流侧以定功率方式运行,故障发生后,HVDC系统将优先保证输电功率的稳定。此时换流母线的电压水平出现下降,为维持输电功率,直流电流会升高,这增加了对系统换相角和无功功率的需求。所以,HVDC系统整流侧以定电流方式运行相比于定功率方式对于风光火打捆系统的暂态稳定性更有利。

3.4 虚拟同步发电机控制仿真分析

为验证VSG控制算法与打捆系统送端风、光两机组结合后的可行性及有效性,仍以图4系统C组数据为基础仿真分析风、光机组有无VSG控制策略的区别。设置三相故障发生仿真3秒时交流一回线路50%处,故障持续0.1秒后故障清除。VSG仿真参数如表4所示。

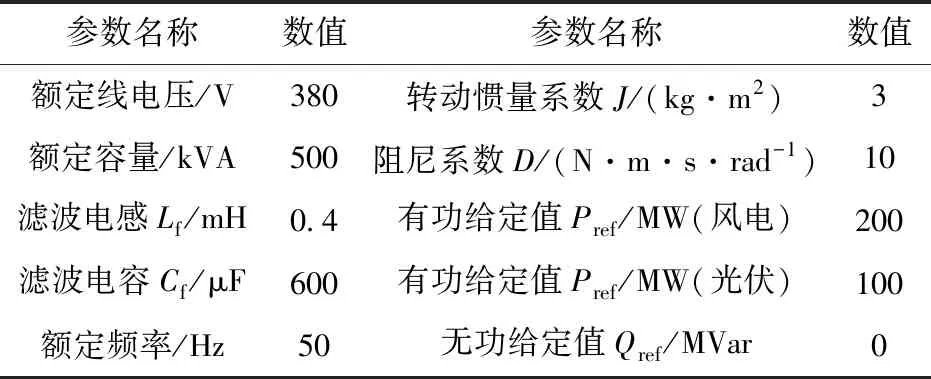
表4 VSG仿真参数

扰动发生后,可以看到图9～10中,风电和光伏机组输出功率受扰后的首摆幅度、波动频率以及恢复速度都优于VSG策略加入前。而从图11看,母线频率受扰后的摆动幅度和恢复到稳态的时间也都有所优化。图12中可以观察到,送端火电机组的功角摆幅有所减小,恢复速度也更快,VSG控制策略有效地改善了火电机组的功角响应。从各项仿真结果可以看到,送端系统风电与光伏机组并网换流器中加入VSG控制策略后,风、光机组受扰后的各项输出响应均有所优化,系统送端表现出了更好的惯量特性。

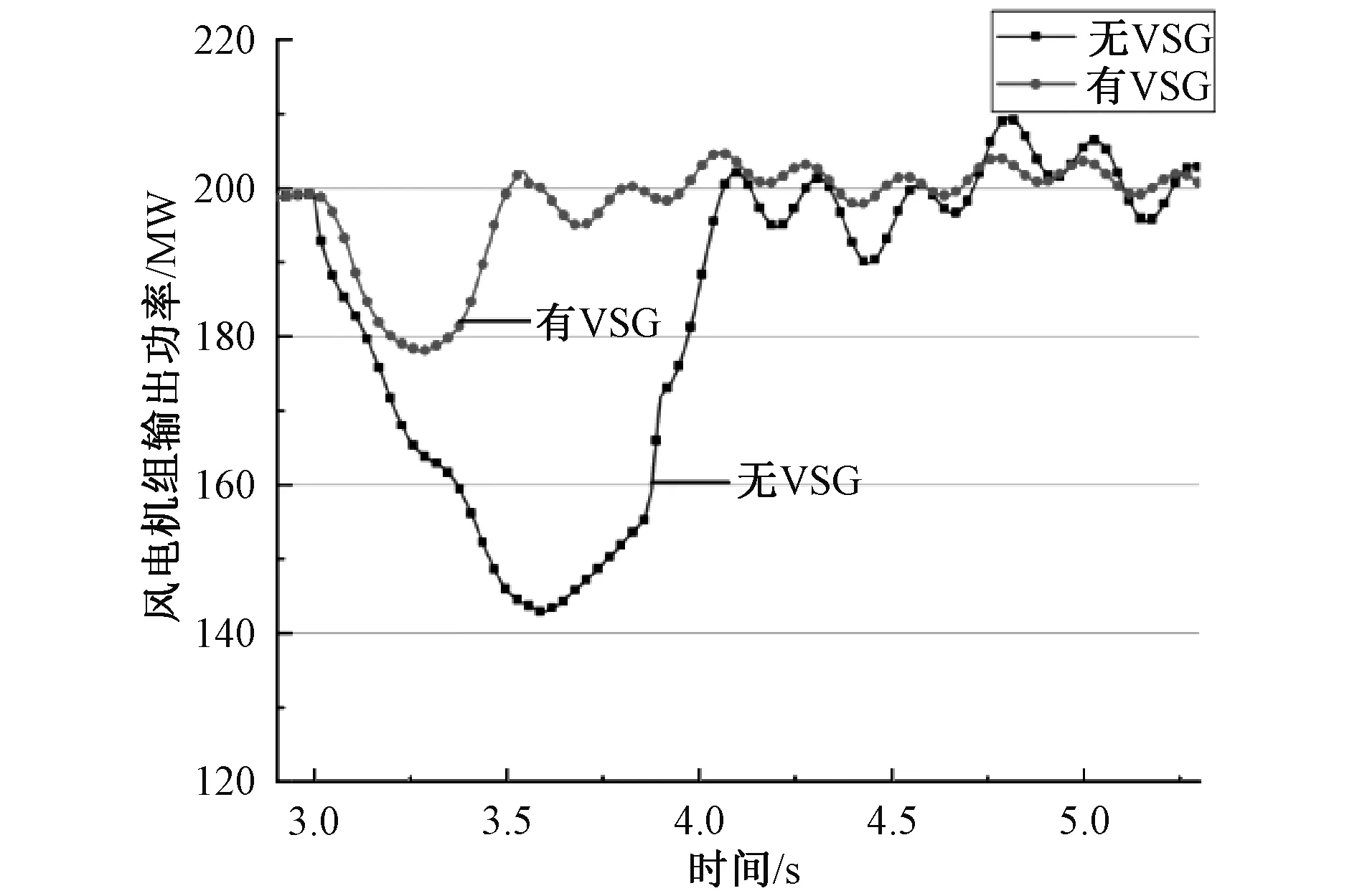
图9 风电输出功率对比图

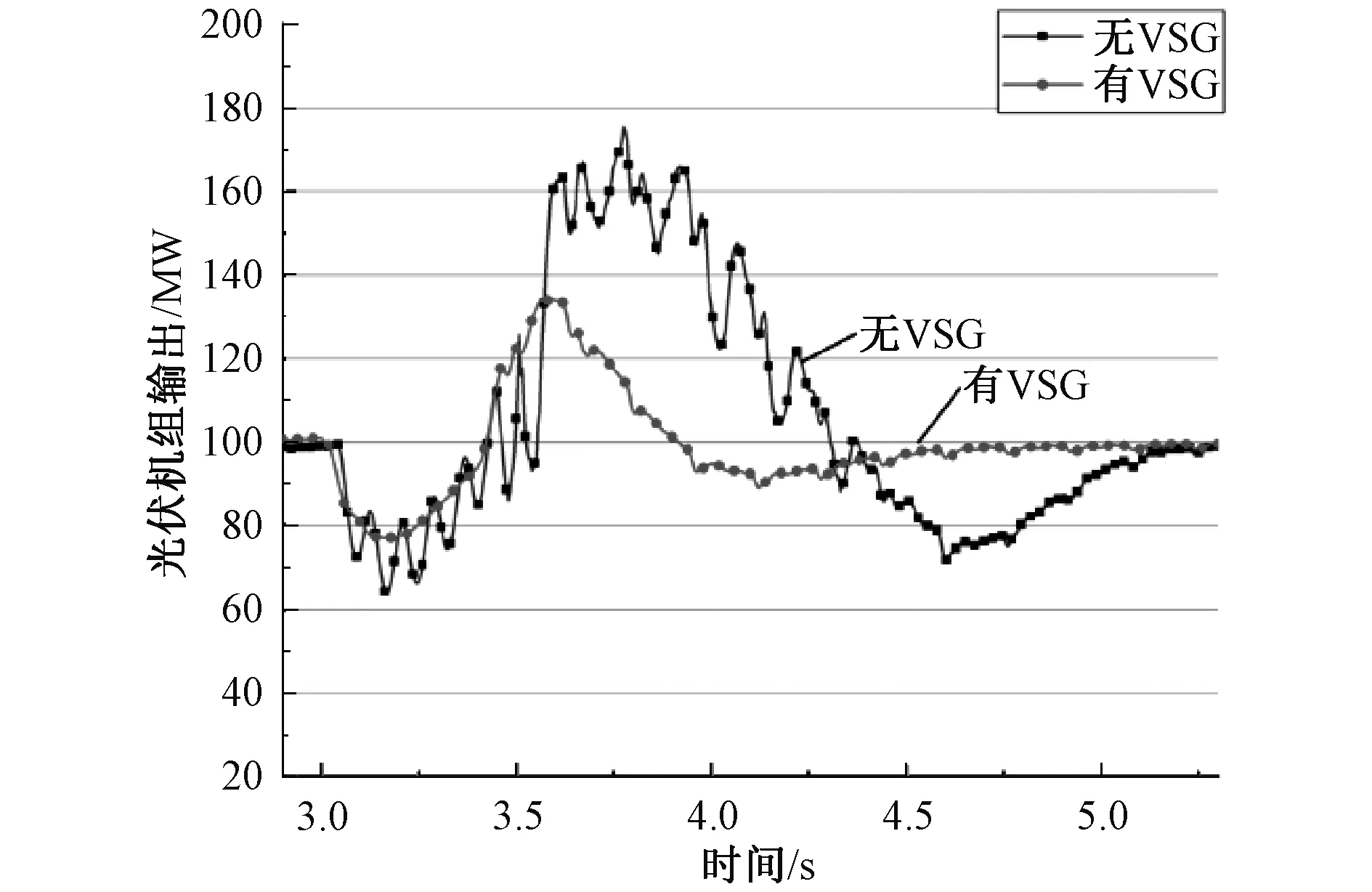
图10 光伏输出功率对比图

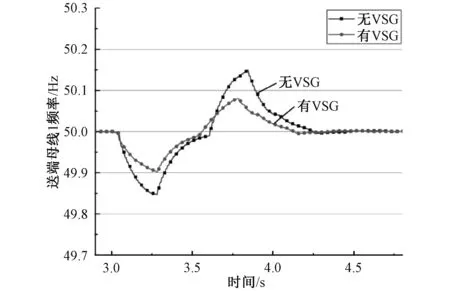
图11 汇流母线1频率对比图

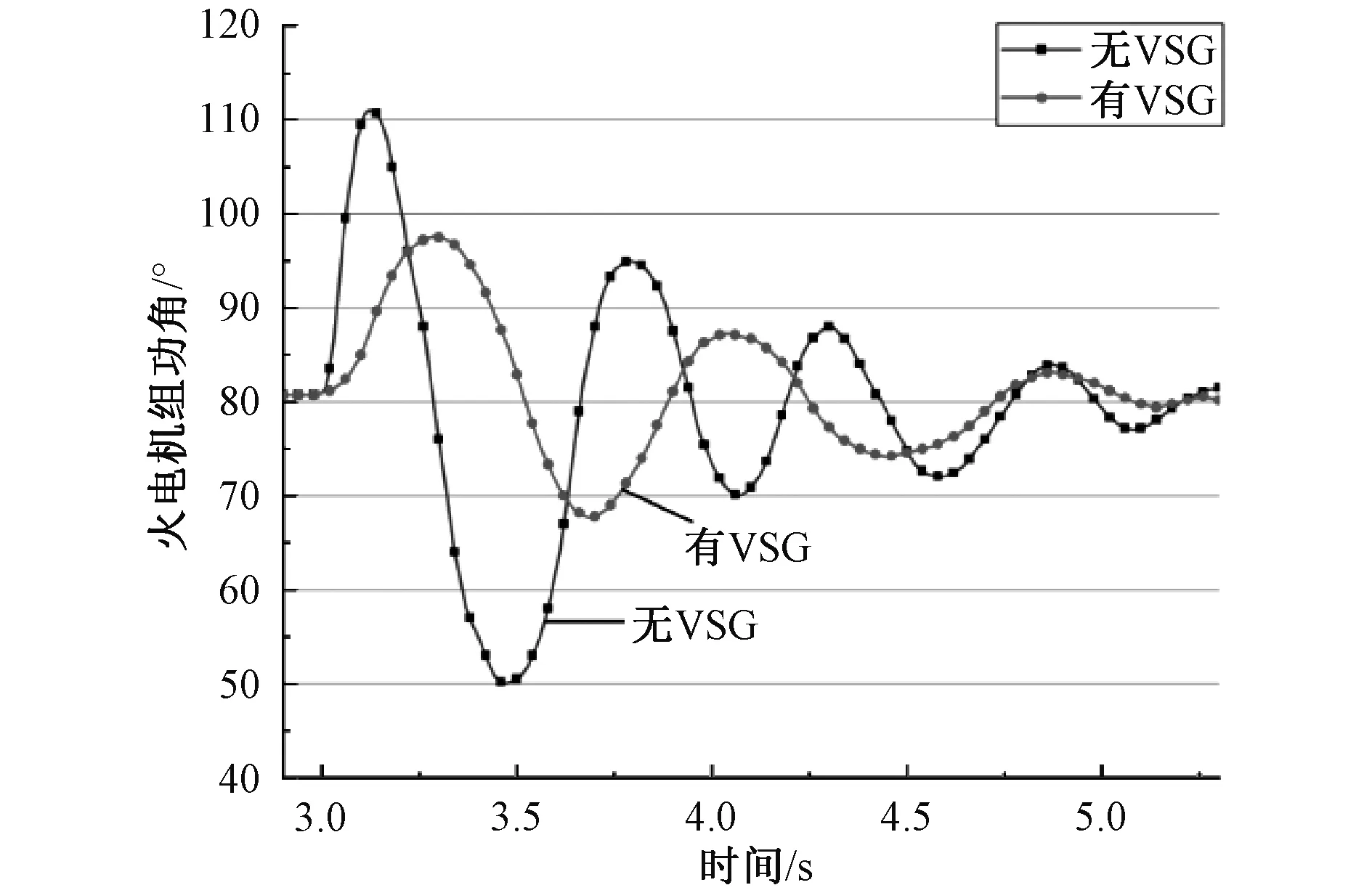
图12 火电机组功角对比图

4 结 论

对典型风光火打捆交直流混联外送系统的暂态稳定性的仿真分析和基于虚拟同步机策略解决打捆系统送端低惯量问题都具有着重要意义。本文基于PSCAD仿真软件搭建了风光火打捆外送系统的基础仿真模型,深入分析了交流故障类型、风光火占比以及直流控制方式对打捆系统暂态稳定的影响,并通过将虚拟同步机策略与打捆系统中的风电、光伏机组有效结合给予了系统送端虚拟惯量支撑,通过仿真得出了与理论相符的结论:

(1)三相故障对比单相故障对系统稳定的影响更加严重。维持送端总出力不变,当系统受端非无穷大时,随着风电、光伏出力占比的增加,打捆系统的暂态稳定性呈现出先提升后降低的趋势,针对功角特性存在最优配比。

(2)HVDC系统整流侧采取定电流方式比定功率方式拥有更优的总体暂态稳定性。

(3)VSG策略与打捆系统送端风、光机组结合能有效改善送端系统机组受扰后的响应,使系统送端表现出了更好的惯量特性。