基于ESPRIT-PSA与LightGBM算法的感应电动机转子断条数目诊断新方法
2023-10-16许伯强王晨曦何俊驰
许伯强, 王晨曦, 何俊驰
(1.华北电力大学 电气与电子工程学院,河北 保定 071003;2.广东电网有限责任公司肇庆供电局,广东 肇庆 526060)
0 引 言
转子断条是异步电动机的一种典型故障模式,其故障比例仅低于轴承故障和绕组故障,占总故障类型的7% ~ 10%[1]。若不及时处理,随着故障程度加深会极大降低电机的使用寿命[2]。因此转子断条故障诊断对提高异步电动机运行的可靠性起着至关重要的作用。
由文献[3]可知,转子断条会令电机电流和磁场产生周期性变化,这将导致电机定子电流中出现频率为(1±2s)f1为(s为电机转差率,f1为供电频率)的边频分量。通过测量该边频分量达到转子断条诊断目的的方法称为电机定子电流信号分析方法MCSA (Motor Current Signal Analysis)[4]。关于此法的研究已经较为完善,然而在低转差率的情况下,电机定子电流的边频分量会被工频分量淹没[5];另外,电机在负载波动时,电流也可能会产生(1±2s)f1频率的分量,为MCSA类方法的诊断带来困难[6]。
为此文献[7]对瞬时无功功率信号进行频谱分析进而实现对电机转子断条故障的诊断,其本质为:当转子发生断条故障时,其瞬时无功功率的表达式中会出现频率为2sf1的故障分量。这类方法通常称为电机瞬时无功功率信号分析(MIRPSA)类的转子断条故障诊断办法[8]。其优势在于只需滤除瞬时无功功率频谱中的直流分量就能准确分析出故障分量,因此只要能够有效区分瞬时无功功率频谱中的故障分量是由转子断条故障引起的还是由负荷波动等非故障因素引起的,即使在低转差率状况下,MIRPSA类方法也能实现准确的故障诊断[9]。
需要注意的是,虽然文献[10]推导了感应电动机发生转子断条故障时瞬时无功功率的解析式,但是在实际诊断中发现基于此式的诊断结果与转子实际断条数目有较大偏差。并且,通过快速傅里叶变换FFT(Fast Fourier Transform)对故障分量进行计算需要较高的信号采样时长。有鉴于此,本文将采用旋转不变信号参数估计技术(ESPRIT)、模式搜索算法(PSA)与轻型梯度提升机(LightGBM)结合的方法进行转子断条故障诊断。
本文首先采用ESPRIT-PSA技术测量转子发生断条故障时瞬时无功功率的2sf1分量,经实验验证,ESPRIT-PSA能够准确测定2sf1分量的幅值;同时,此方法即使针对短时信号仍能实现高频率分辨力,可有效回避负荷波动的影响。之后,计算出与电机瞬时无功功率的2sf1分量对应的各相电压、电流等23个变量作为故障特征,并通过分类器计算出故障特征所占权重。继而选择权重最高的5个变量作为LightGBM学习的特征变量并通过5折交叉验证测试模型准确性。最后将LightGBM训练所得模型与其他主流的机器学习模型进行对比以验证该方法的有效性。
1 ESPRIT-PSA算法
基本的ESPRIT方法可以视为是一种最小二乘估计子,其作用是将原观测空间约束到一个维数等于谐波分量个数的子空间之中。虽然ESPRIT突破了傅里叶变换在频率分辨力上的局限性,但无法直接使用传统的ESPRIT方法求解广义特征问题[11]。因此本文采用在工程实际中广泛应用的总体最小二乘ESPRIT算法,即TLS-ESPRIT。即使如此,其对故障特征分量的幅值大小的计算仍存在较大偏差[12],因此本文采用ESPRIT与PSA结合的方法以确定故障特征分量的频率和幅值。ESPRIT-PSA提取故障特征流程如图1所示。
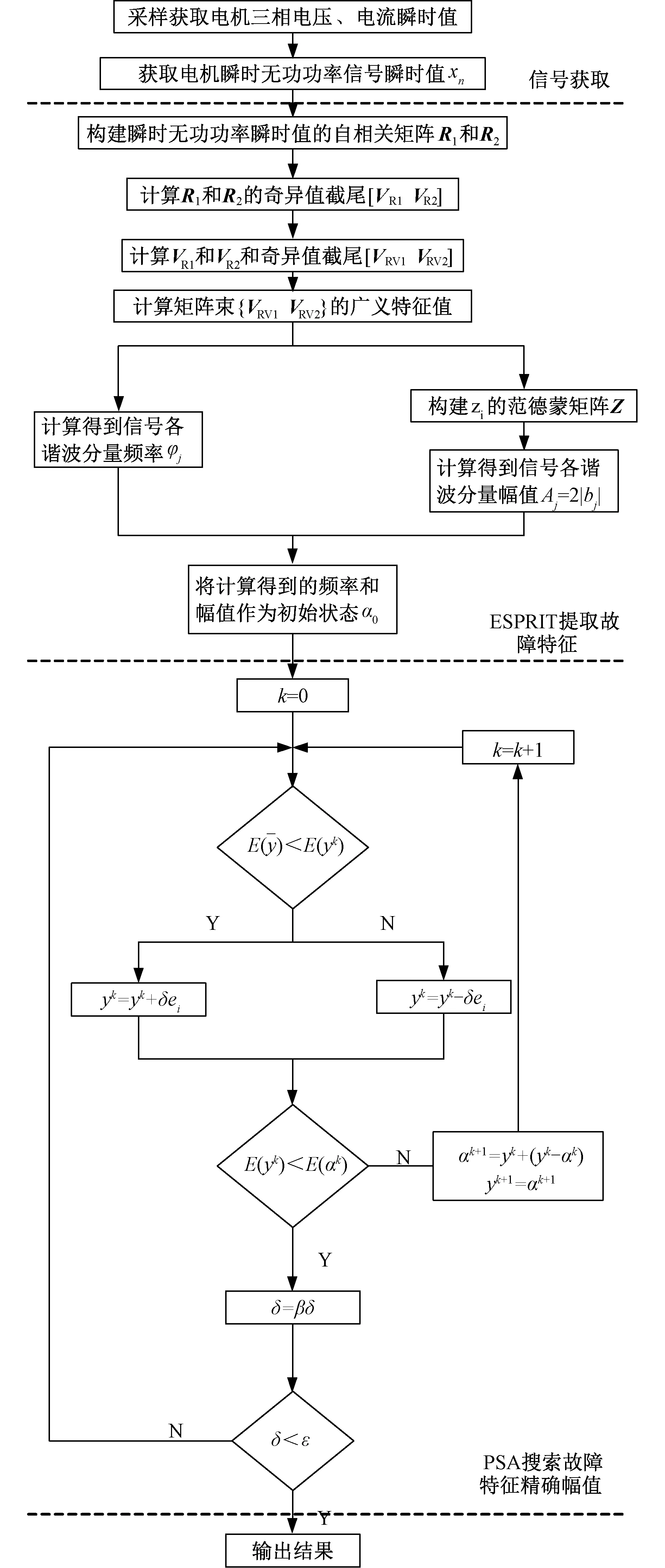
图1 ESPRIT-PSA提取故障特征流程图
图1中,自相关矩阵:R1=Cxx,R2=Cxy,yn=xn+1。
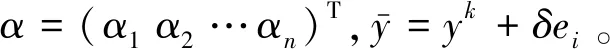
异步电动机发生转子断条故障后,其瞬时无功功率表达式可由式(1)模拟,以此分析ESPRIT-PSA算法应用于转子断条故障诊断的可行性。在实际仿真时,选取转差率s=0.3%并添加了一个方差为0.5、均值为0的高斯噪声,以模拟实际运行时电机转差率甚低和可能存在测量信号被干扰的情况,仿真结果如表1所示。

表1 ESPRIT-PSA仿真计算结果
(1)
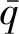
由表1数据可知:ESPRIT-PSA算法能够准确确定转子断条故障特征分量的幅值和频率。根据式(1),对Aq、γ、s、f1的取值进行随机、组合性地变换而进行了大量测试,其结果与表1相符。
至此,毋庸置疑:ESPRIT-PSA算法可以用于转子断条故障的诊断;但是,仅依靠测量瞬时无功功率2sf1分量的幅值和频率,再代入现有判据的方法无法准确诊断出转子断条故障的数目[10]。
2 LightGBM算法
基于上述存在的问题,本文采用LightGBM训练针对转子断条故障的分类模型以代替传统的公式判据。LightGBM算法是Boosting算法的新成员,且是由微软公司开发的机器学习方法。LightGBM算法是对GBDT(Gradient Boosting Decision Tree)算法的高效实现。与其他的机器学习算法相比,LightGBM算法具有这些优势:训练效率更高;占用内存较低;准确率更高;支持高效并行化学习;可以处理大规模数据[13]。
2.1 生成数据集
首先在使用LightGBM训练模型前,需要构建输入数据集和对应标签。首先将ESPRIT-PSA算法计算得出的Aq作为第一个特征变量置入数据集中。再通过对采样获得的电机三相电压、电流的瞬时信号进行计算,得到定子三相电压幅值、三相电流幅值、三相电压相位、三相电流相位、正序电压有效值、负序电压有效值、零序电压有效值、正序电流有效值、负序电流有效值、零序电流有效值、正序阻抗模值、负序阻抗模值、零序阻抗模值、平均有功功率和平均无功功率,这23个与Aq对应的衍生故障特征。将这23个与Aq对应的故障特征置入数据集,由此得到数据集{X}。
标签分类转子断条数目,记为0~2分别对应正常、转子有1根断裂和转子有2根断裂3种状态,形成标签数据集{Y}。
2.2 LightGBM模型
LightGBM是基于预排序的决策树算法[14],其目标函数如下:
(2)
本文为减小模型过拟合度,定义LightGBM损失函数如下:
(3)
式中:l表示预测值与真实值的差距,Lm表示m次迭代后的损失函数,γ和λ是设定的参数,T为叶子节点数,wj表示第j个叶子节点的输出值。
2.3 基于LightGBM的模型构造
在训练模型前,需要将数据集{X}及其对应的标签{Y}以8∶2的比例分割为训练集和测试集。之后采用GridSearchCV(网格搜索)进行超参数调优,模型最优参数如表2所示。
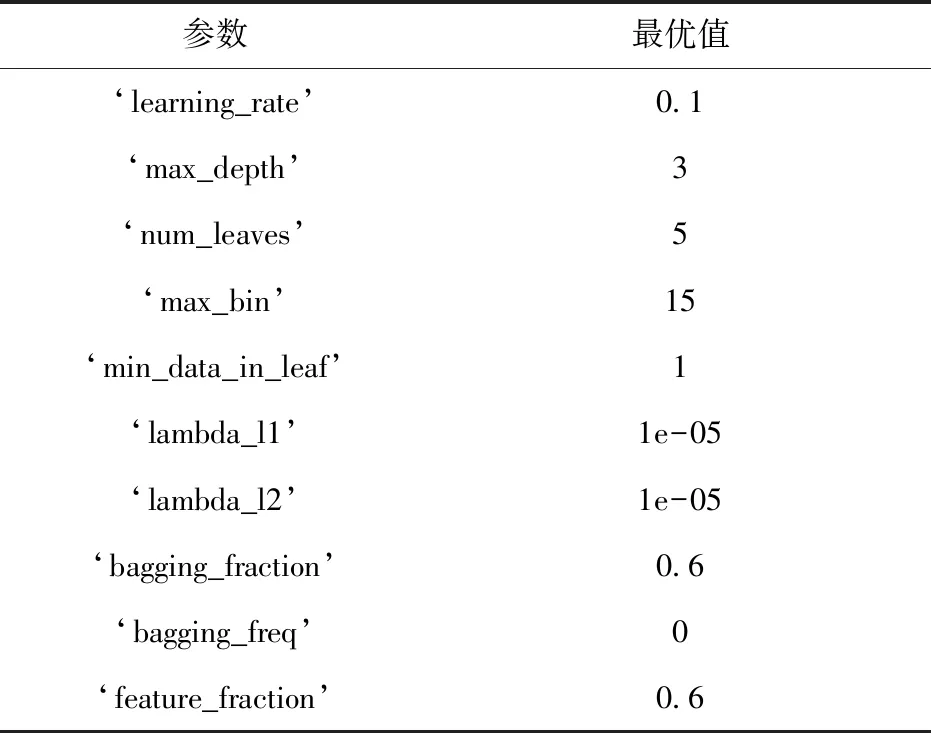
表2 超参数调节
最后根据此最优参数设定LightGBM模型各变量的值并输入数据集训练模型。
3 基于ESPRIT-PSA与LightGBM算法的异步电动机转子故障诊断方法
3.1 基本流程
本文的故障诊断基本流程如下:
(1)测取定子三相电流信号瞬时信号和定子三相电压信号瞬时信号。
(2)由定子三相电压电流计算得到瞬时无功功率并滤除其直流分量,记为qA。
(3)通过滑动窗口法(窗口中包括1 s的数据)对qA做ESPRIT-PSA分析,确定其p个主频率分量的幅值、频率和初相角。取其中频率为2sf1的分量,其幅值大小记为Aq。
(4)构建训练LightGBM模型的输入数据集和对应标签。
(5)将Aq在内的5个变量作为特征量与故障标签整理形成10 535×5的二维输入数据集{X}和10 535×1的标签{Y}。
(6)将数据集以8∶2的比例分割为训练集和测试集,将其代入LightGBM模型中训练,并进行参数调优已获得诊断效果最好的模型。
瞬时无功功率特征分量的幅值Aq、平均有功功率P、平均无功功率Q、A相电压幅值Um、A相电流幅值Im均是通过滑动窗口法(窗口中包括时长1秒的数据)对采样信号进行处理得到的。具体而言,电机正常时,满载得到1 201组样本数据,半载、空载每种负载下可通过上述工作得到1 050组样本数据,即包括3 301组样本数据;电机转子1根断条故障和转子2根断条故障时,满载各得到1 317组数据,半载、空载每种负载情况下各得到1 150组样本数据,即两种状态各包括3 617组样本数据,则3种状态一共包含10 535组样本数据。
3.2 实验结果与分析
实验电动机为一台Y100L-2型三相异步电动机,额定电压380 V,额定功率3 kW,额定频率50 Hz。为进行转子断条实验,确保故障转子确实达到了工程实际的故障程度,除其正常转子外,另配备了两个故障转子(距端环10 mm处钻孔,深度10 mm,直径6 mm)用以模拟断条故障。这两个故障转子分别存在一根断裂导条和连续两根断裂导条,如图2所示。

图2 实验设备
负载采用直流测功机,通过对直流电机的调整以使异步电动机分别处于满载(转差率s约3.84%)、半载(转差率s约1.94%)和空载(转差率s约0.33%)的状态,并对两个故障转子进行大量实验。以电机处于空载,转子发生连续两根导条断裂故障时为例,某时间段电机瞬时无功功率的频谱如图3所示,具体实验数据可参考表3。
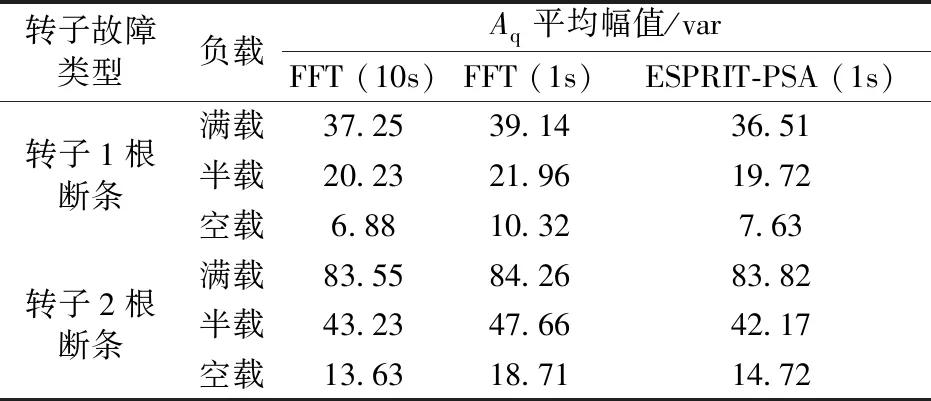
表3 转子断条故障实验结果
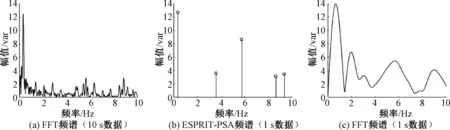
图3 空载情况下瞬时无功功率频谱
本文中瞬时无功功率的FFT频谱均为滤除其直流分量后进行细化FFT分析后的频谱。
由表3可知:在满载、半载的情况下,对10 s数据进行细化FFT分析、对1 s数据进行细化FFT分析和对1 s数据进行ESPRIT-PSA算法分析,三者计算得到的Aq幅值结果基本吻合。但对1 s数据进行细化FFT分析,发现其在电机空载时计算数据误差过大并且对于1 s数据的处理结果,ESPRIT-PSA算法分析的瞬时无功功率幅值更接近对10 s数据进行细化FFT分析的结果。因此ESPRIT-PSA算法是更为理想的故障特征提取方法。
这就说明用ESPRIT-PSA算法测量转子断条的瞬时无功功率是可行的,并且由于其只需要1 s的数据即可保证其故障测量性能,此法也可以有效避免负荷波动的情况。
表4为特征权重排名,权重由分类器依据特征对分类结果影响程度自动计算得出。具体的权重计算方法可参考文献[15]。为避免故障特征太多在高维空间中出现样本稀疏、距离计算困难等问题,本文选择权重占比前5的变量作为LightGBM模型学习的特征变量。

表4 LightGBM特征权重排名
本文特征量的数量K最终确定为5是通过多次实验,综合考虑模型过拟合度及正确率后,选择特征权重排名前5的特征进行模型训练。结果如表5所示。

表5 模型选取不同数量特征量的训练结果
表中的实验所用数据为相同数据,且模型已经过最优参数调整。由表中数据可知,当n=5时和n=6时,模型精度最高。但n=6时,其5折交叉验证正确率较低,这是因为特征量的数量增多容易导致模型过拟合。因此本文最终选择的特征量的数量为5。
3组独立实验下,LightGBM训练的数据集分类精度平均结果如表6所示。由表6可知,最优参数下的LightGBM训练模型在不同负载情况下都能达到99.9%的分类准确度。为防止此结果是由训练集和测试集的选择不佳而导致的,本文选择使用5折交叉验证的方法对模型性能进行评估。所谓5折交叉验证,就是将数据集随机等分为5份,每次取其中4份作为训练集,用剩下的1份作为测试集,训练5次得到5个模型,最后将这5个模型的平均测试效果作为最终的模型结果。

表6 调优后的LightGBM准确率
为充分验证所提模型性能,本文将LightGBM算法与经过超参数调优的随机森林、XGBOOST、AdaBoost、多层神经网络这几种主流的机器学习算法进行对比。测试将采用8∶2的比例分割数据。即将总数据量的80%作为训练集,剩余20%作为测试集。将分类后的数据集代入各分类器中进行训练,并对模型进行参数调优以获得效果最优的模型。在3组独立实验下,各分类器最优模型的5折交叉验证平均准确率、每次训练所用平均时间以及精确率和召回率如表7、表8和表9所示。
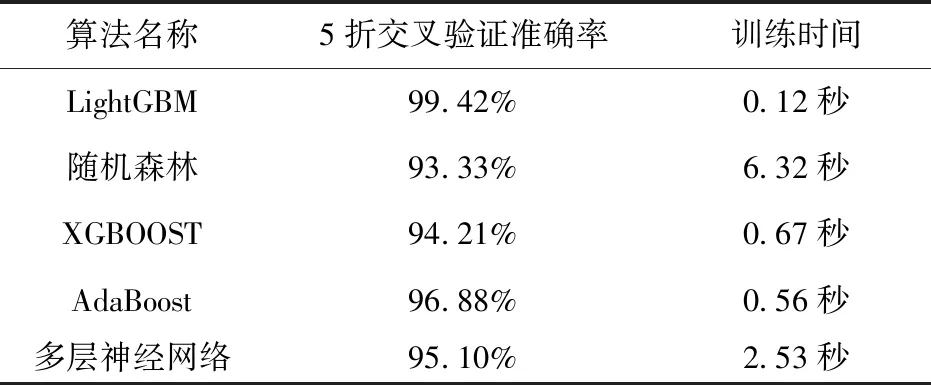
表7 各算法交叉验证准确率及时间对比

表8 各算法精确率对比
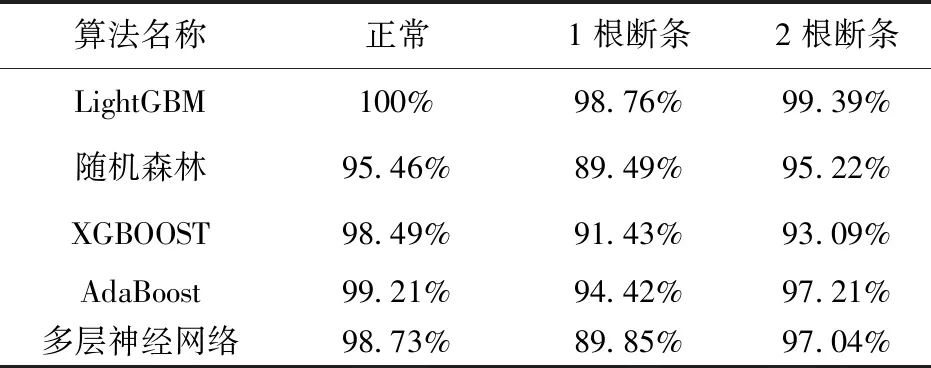
表9 各算法召回率对比
表7、表8和表9数据表明:LightGBM算法在模型准确率、精确率、召回率等方面均明显优于其他主流算法。
基于LightGBM算法的转子断条数目诊断结果如表10、表11和表12所示。
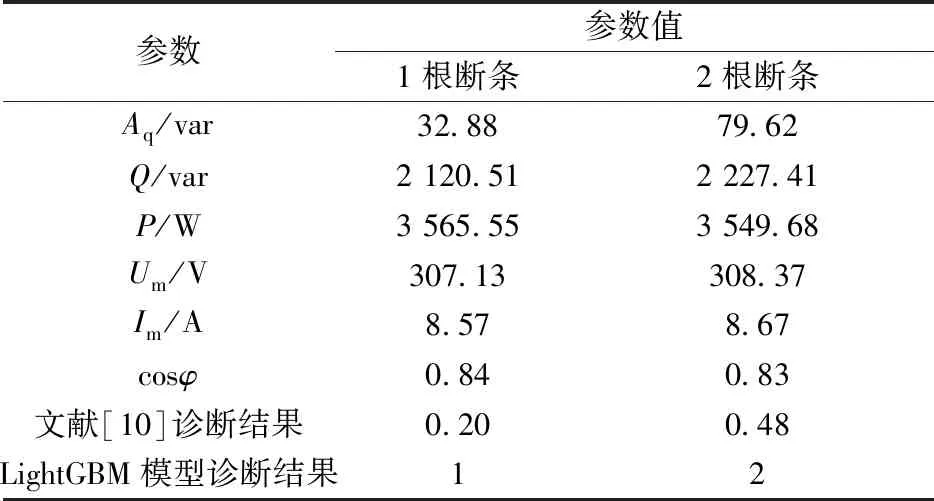
表10 电机满载情况下的诊断结果

表11 电机半载情况下的诊断结果
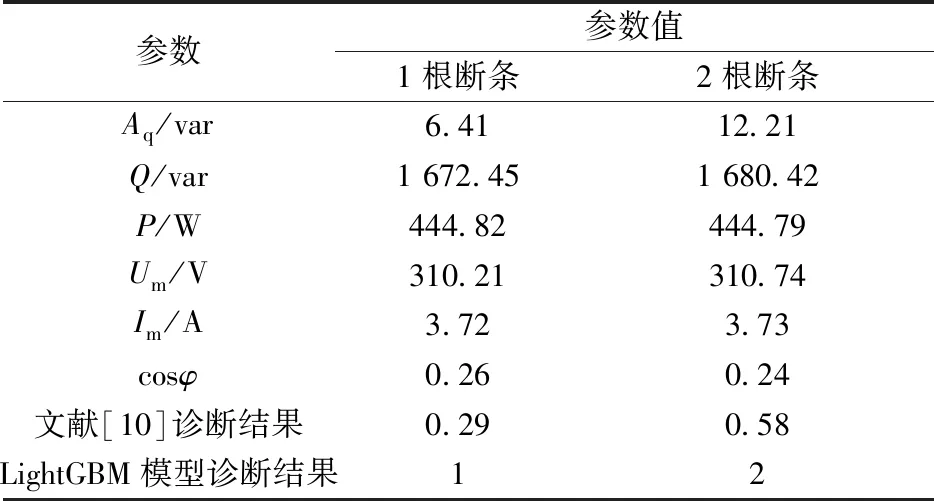
表12 电机空载情况下的诊断结果
表10、表11和表12的数据表明:现有判据对转子断条数目的诊断结果存在较大偏差。虽然具有一定参考价值,但在实际应用中仍需根据情况对其结果进行校正优化,存在很大限制。而基于LightGBM算法的转子故障诊断模型在不同负载情况下均能准确诊断转子故障数目,可以作为理想模型进行电机转子故障数目诊断。
4 结 论
本文提出了一种基于ESPRIT-PSA与LightGBM算法结合的转子断条故障诊断新方法。通过实验的方法得出以下结论:
(1)即使对于短时信号,ESPRIT-PSA算法仍具备较高的频率分辨力,并且可以准确估计转子断条故障的特征分量——瞬时无功功率的2sf1分量。
(2)在ESPRIT-PSA估计的基础上,结合细化FFT分析计算得出与之对应的定子单相电压幅值、电流幅值、平均有功功率等变量可以为机器学习提供可靠的分类依据。
(3)基于LightGBM算法的故障诊断模型以瞬时无功功率的2sf1分量为主要特征,经实验验证,即使在电机空载低转差率情况下仍能准确诊断转子断条数目。
然而由于实验条件的限制,本文并未讨论在电机负载变化、电压波动时该方法的有效性。该领域的研究具有重要的意义,因此在未来研究中我们将重点解决这些问题。
