LW30-252型SF6高压断路器潜伏性故障声信号识别方法
2023-10-16刘云鹏廖思卓王博闻
刘云鹏, 韩 帅, 廖思卓, 杨 宁, 高 飞, 王博闻
(1.河北省输变电设备安全防御重点实验室(华北电力大学),河北 保定 071003;2.中国电力科学研究院有限公司,北京 100192)
0 引 言
高压断路器作为一种重要的输变电设备,其操动机构能否正确动作,直接关系到系统的安全运行。根据统计表明,高压断路器的操动机构机械故障占全部故障的70%~80%[1]。开展高压断路器操动机构机械状态评估与故障诊断技术具有重要意义[2]。
目前,对于断路器机械故障诊断的研究通常以振动或声纹信号为基础,配合人工神经网络、动态时间规整和支持向量机等算法进行模式识别[3]。振动信号检测方面:文献[4]基于断路器故障时振动信号的发生时间产生变化的特点,将振动信号的时间参数作为故障特征,采用FCM识别断路器的故障类型;文献[5]研究了单类支持向量机在断路器诊断中的应用,将正常状态下断路器振动信号作为训练样本,利用高斯核的支持向量机进行训练,以此来判断断路器是否发生故障;声纹信号检测方面:文献[6]利用小波包处理断路器声纹样本,用RVM对故障信号进行诊断,最终诊断结果具有较高的准确率;文献[7]以EEMD-关联维数作为特征向量,采取BP神经网络处理该向量,将识别率进一步提升。而随着深度学习技术的发展,相关方法已在语音识别、说话人识别等领域进行了广泛应用,在断路器故障识别方面也有部分应用报道,文献[8]使用小波时频图与卷积神经网络相结合对断路器故障进行了故障识别,但其所识别的故障皆为较为严重的故障,时域与频域信号差异极为显著,而初期的轻微故障未有提及,文献[9]使用的LSTM-CNN断路器故障识别模型在正常与某单一故障分类问题上具有极高准确率,但涉及到更贴近实际应用的多分类场景时则准确率有所下滑。高压断路器实际应用中的各类常见故障(拒动故障、误动故障、卡涩故障和断裂故障等)大多与其操动机构密切相关,而此类故障往往是由潜伏性机械故障(油缓冲器漏油、弹簧疲劳、传动销磨损等)逐步发展累积形成的,潜伏性故障早期特征不够显著,如不及时发现处理易发展成严重故障造成更严重的经济损失,当前针对潜伏性故障的研究主要关注于过热和放电[10],而机械类潜伏性故障研究较少,因此需要对其特征提取与早期识别开展进一步研究。
断路器机械类故障识别主要围绕动作时的振动或声纹信号进行分析与处理,振动与声纹是机械波在不同介质中的不同表现形式,但在实际使用过程中,振动传感需要在断路器上进行打孔部署,且部署位置不同对监测结果具有极强的影响[11],而声纹传感器则无需与断路器本体直接接触,且测点位置少量偏离对声信号的响应差异较小,在现场应用时更为便捷。综上,本文将以更符合现场应用场景的断路器的潜伏性机械故障声纹为对象,进行诊断方法研究。
高压断路器型号较多,本文主要围绕LW30-252型SF6高压断路器展开研究,通过搭建断路器试验平台,采集断路器在不同潜伏性故障运行状态下的声纹信号,并利用一种混合倒谱计算方法与卷积神经网络结构对不同故障状态下高压断路器开合闸声音信号进行区分。首先通过现场采集的方式形成了声信号样本库;然后,分别采用梅尔倒谱系数(Mel Frequency Cepstral Coefficient, MFCC)、伽马通滤波倒谱系数(Gammatone Filter Cepstral Coefficient, GFCC),幂律归一化倒谱系数(Power-Normalized Cepstral Coefficient, PNCC)对原始信号进行降维与初步特征提取;最后,引入卷积神经网络(Convolutional Neural Networks, CNN)作为分类器,与MFCC、GFCC、PNCC三重特征形成的混合倒谱(Mixed- Cepstral Coefficient)共同构成6种运行状态的分类模型,并通过数据集验证模型的有效性。
1 MCC-CNN故障声信号识别方法
断路器声信号识别整体流程如图1所示,首先将由传声器采集的断路器动作声信号转化为具有时域频域两个维度的时频谱图,然后通过计算MFCCs、GFCCs与PNCCs等3种倒谱对原始时频谱进行特征提取和降维,最后使用卷积神经网络作为分类器进行故障类型识别。整个流程可大致分为声信号的采集、预处理与模式识别三部分,其中声音信号的预处理方法最为重要,其主要作用是对断路器原始时域信号进行特征提取和数据压缩,从而减少后续识别模型的运算量并提升识别效果。

图1 断路器声信号辨识流程
1.1 断路器动作声信号时频谱计算
断路器声信号的时域信号为一维的脉冲信号,其特征性信息不够明显,可使用短时离散傅里叶变换的方式将其转化为二维时频谱,有利于提高深度学习模型的识别速度与识别准确率。短时傅里叶变换过程中需要进行分帧、加窗以及离散傅里叶变换。其中,窗函数通常可选择汉明窗,以减少傅里叶变换造成的频谱泄漏,长度为N的汉明窗w(n)公式如下:
(1)
将离散后的时域帧进行短时离散傅里叶变换即得到时频谱矩阵:
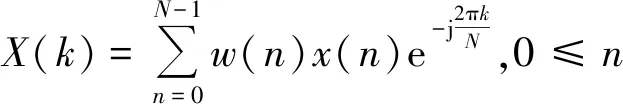
(2)
其中,k为频点序号,x(n)为原始离散时域信号。
1.2 混合倒谱特征计算
断路器潜伏性故障一般特征不明显,因此在进行断路器声纹诊断时,要在保证声信号辨识速度的前提下提取其声纹特征,从而提高识别准确率。而在语音识别领域广泛使用的倒谱系数计算方法能够对样本进行数据压缩的同时保留合闸关键声纹信息,从而实现断路器声信号的压缩与特征提取,有助于改善后续衔接的卷积神经网络等分类器的诊断速度与诊断准确率。
各种倒谱系数都具备信号降维与特征提取功能,然而不同倒谱系数都具有各自优势和局限性,因此许多研究[12,13]将多种倒谱进行混合使用,以获得更好的特征提取效果。在各类倒谱系数中,MFCC的构建基础是听觉模型,GFCC的构建基础是耳膜模型,而PNCC在噪声背景下的声音特征提取方面更具优势,以上倒谱在语音识别领域都已经得到了一定程度的应用[14],因此本研究选取MFCC、GFCC[15]、PNCC[16]作为基础倒谱特征,构成倒谱特征矩阵,用于后续的特征融合和声信号识别,计算流程如图2所示。
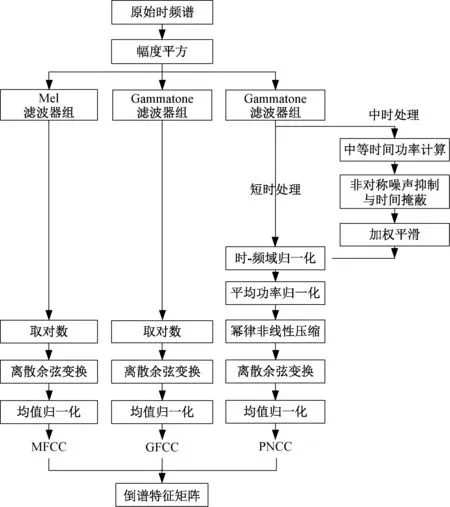
图2 声信号倒谱特征矩阵计算流程图
(1)MFCC计算
MFCC是基于人耳听觉感知特性的一种倒谱参数,在频域人耳听到的声音高低与频率不成线性关系,而在Mel域,人耳感知与Mel频率是成正比的。其关系可以用下式表达:
Mel(f)=2 595 lg(1+f/700)
(3)
梅尔频率倒谱系数的计算是以帧为单位进行的,以下为梅尔频率倒谱系数的具体计算步骤:
首先按式(1)计算得到每帧频谱X(k),k为频点序号,对每帧X(k)取模后平方得到功率谱。将功率谱通过频域为三角形的Mel尺度滤波器组得到新的参数R(k),如式(4)所示,滤波器组频率下限为fmin,上限为fmax,G为Mel滤波器数量。
R(k)=X(k)Hp(k)
(4)
其中,Mel滤波组Hp(k)由滤波器编号p、Mel滤波器数量G以及滤波器中心频率f(p)决定,计算公式如下:
(5)
然后将R(k)取自然对数:
(6)
接着通过离散余弦变换(DCT)得到W维MFCC,在断路器识别任务中,W可设为G:
(7)
最后需要进行均值归一化。经上述步骤便可得到G维的MFCC。
(2)GFCC计算
GFCC的提取过程与MFCC提取过程几乎相同,两者区别在于功率谱通过的滤波器组是由G个不同尺度参数和形状参数的伽马滤波器组成的Gammatone滤波器组,而非Mel尺度滤波器。滤波器组频率上下限同样为fmax与fmin,后续计算步骤也相同。
(3)PNCC计算
PNCC的提取过程的前两个步骤与GFCC相同,当功率谱通过Gammatone滤波器后得到P[m,l],其中,m表示帧数,l表示信道编号。其中,M为平滑窗口的大小,一般将每一帧与前后两帧做平滑处理,此时M=1计算中时平均功率:
(8)
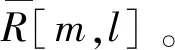
(9)
l1=max(l-p,1)
(10)
l2=min(l+p,N)
(11)
其中,N表示信道数量,p一般设4。
(12)
利用平均功率估计值μ[m]可对T[m,l]进行平均功率归一化:
(13)
(14)
其中,λμ为遗忘系数,一般设置为0.999。k为系数,可设置为任意常数。
为了更加接近人耳听觉神经的压缩感知特性,不同于MFCC所采用对数非线性,PNCC采用幂律非线性压缩:
V[m,l]=U[m,l]1/15
(15)
最终进行离散余弦变换和均值归一化即可得到PNCC。
分别完成MFCC、GFCC、PNCC计算后,将三者合并为一个[Z×G×3]的倒谱特征矩阵,其中Z为时域分量,取决于原始时频谱的时间帧数;G为频域分量,等于各倒谱系数的计算时的滤波器数量,数量越多信息越丰富,而数据量也随之增大,一般设定区间为40到48[12,13],本文中设置为40。
1.3 卷积神经网络计算
由于倒谱特征矩阵是由多个同尺寸二维图谱叠加而成的三维图谱,因此可引入在图像识别领域具有代表性的卷积神经网络(convolutional neural network,CNN)可作为声信号倒谱特征矩阵的分类器。在图像识别领域,CNN通常将彩色图像拆分为红绿蓝(RGB)三个颜色层作为网络的输入层,从而对不同色彩变化的特征进行学习感知。相似地,本研究将声信号的三种倒谱构成的倒谱特征矩阵作为输入层,构建混合倒谱系数-卷积神经网络(Mixed Cepstral Coefficient-Convolutional Neural Network,MCC-CNN)识别模型,从而进行声音分类识别。相较于人工设计的倒谱混合方法,通过深度神经网络的学习机制对三种倒谱进行融合能够使混合倒谱的融合方式具有自适应性。
断路器合闸声纹数据已经进行降维压缩,因此通过一个类VGG[17]的轻量化CNN网络即可实现分类,如图3所示。其中网络结构参数的输入层按照输入样本的尺寸进行设置,而卷积核、池化核尺寸及相应的移动步长选用应用较为广泛的参数,最终经过结构参数调试,确定了包含3个卷积-池化层与4个全连接层的整体网络结构。在网络中,加入了批规范化与概率为0.5的Dropout操作,以防止过拟合与梯度消失[18],详细结构参数如表1所示。
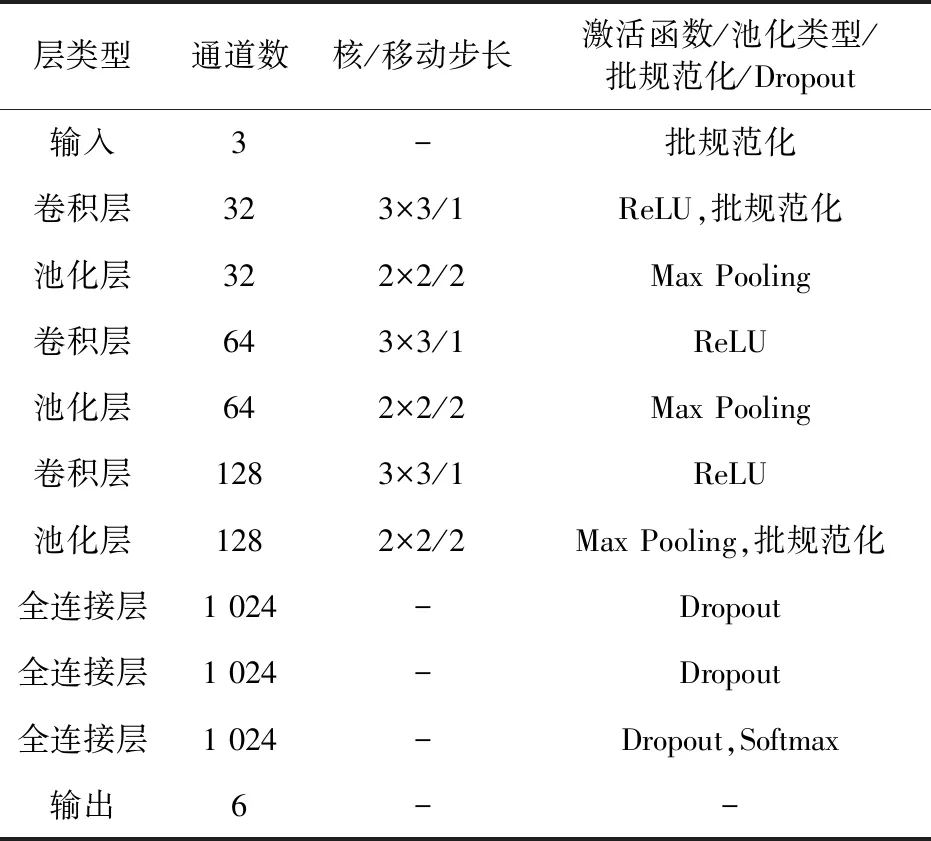
表1 CNN网络结构参数

图3 类VGG的轻量化CNN网络结构
在确定网络参数后需要使用了反向传播算法对CNN进行卷积核W与偏置值b的参数训练。
首先,设定各层的W与b为随机数值,作为初始值。
然后,开始迭代训练。以一组数量为m为样本批次为例,设定样本编号为i,层编号为l。将CNN输入层的数值分为全连接层、卷积层、池化层和输出层四种情况进行前向传播计算,公式分别如下:
ai,l=σ(zi,l)=σ(Wlai,l-1+bl)
(16)
ai,l=σ(zi,l)=σ(Wl*ai,l-1+bl)
(17)
ai,l=pool(ai,l-1)
(18)
ai,L=softmax(zi,L)=softmax(Wl*ai,L-1+bL)(19)
其中,ai,l与zi,l分别为第i个样本在第l层的输出结果和卷积结果,σ为激活函数,pool为池化函数,softmax为归一化指数函数。当前向传播计算至输出层后,通过损失函数计算输出层的损失值δ,并开始反向传播计算各层损失值,按层的类型分为全连接层、卷积层和池化层三种情况进行前向传播计算,公式分别如下:
δi,l=(Wl+1)Tδi,l+1⊙σ′(zi,l)
(20)
δi,l=δi,l+1*rot(Wl+1)⊙σ′(zi,l)
(21)
δi,l=upsample(δi,l+1)⊙σ′(zi,l)
(22)
其中,δi,l为第i个样本在第l层的损失值。rot为翻转函数,可将卷积核上下、左右各翻转一次。upsample为上采样函数。跟据δi,l计算结果即可更新第l层的Wl、bl,更新公式为:
(23)
(24)
α=η/m
(25)
其中,η为学习率。
最终,不断更新的Wl、bl的变化值都小于停止迭代阈值,则跳出更新循环。
2 潜伏性机械故障模拟及数据采集
高压断路器主要部件包括储能单元、传动单元和控制单元三大部分,LW30-252型SF6高压断路器及其内部的CT26型弹簧操动机构实物图如图4所示,CT26型弹簧操动机构结构示意图如图5所示,其结构紧凑、集成度高,但在使用过程中也面临机械故障等共性困扰[19]。因此,本文基于CT26弹簧操动机构的结构原理,围绕油缓冲器漏油、合闸弹簧疲劳、传动轴销磨损、主轴卡涩、地脚螺栓松动5种典型高压断路器潜伏性机械故障展开人为故障设置与模拟实验,为后续的声纹分类实例构建数据集。

图4 LW30-252型SF6高压断路器及操动机构

图5 CT26弹簧操动机构结构图
2.1 高压断路器试验平台及故障设置
(1)油缓冲器漏油故障
油缓冲器是稳定CT26型弹簧操动机构的重要部件,当分合闸动作成功后,能够迅速削弱弹簧盈余的势能与整个机构的动能,避免多余能量冲击本体,造成机构损伤。而缓冲器漏油则会导致其吸收能量的能力下降,若不能早期发现将间接引发诱发机械故障,使整个机构使用寿命大幅下降。故障设置时,将缓冲器内270 mL的缓冲油倒出30 mL,从而削弱其缓冲能力,模拟油液初期泄漏时的状态,如图6所示。

图6 油缓冲器漏油故障模拟设置
(2)弹簧疲劳故障
合闸弹簧是CT26型弹簧操动机构合闸动作的核心部件,当断路器进行合闸动作前,合闸弹簧将电机输入的能量存为弹性势能,当合闸弹簧经过反复压缩和释放,其存储弹性势能的能力将下降,疲劳程度严重时将导致合闸失败,为了模拟合闸弹簧疲劳故障,将预压缩量减少30毫米,减小其弹性势能上限,如图7所示。

图7 合闸弹簧疲劳故障模拟设置
(3)传动轴销磨损故障
传动销是拐臂与断路器拉杆间的重要连接原件,能够起到动能传递与机械固定的作用。若传动轴销出现磨损将导致其连接稳定性下降,将出现传动过程晃动现象,影响合闸动作,严重时将导致拉杆等部位损坏,可人为将传动轴销磨细,模仿其磨损状态,故障设置时,通过打磨将传动轴销直径由16 mm削减至15 mm,扩大了其晃动空间,从而模拟传动轴销轻度磨损故障,如图8所示。

图8 传动轴销磨损故障模拟设置
(4)主轴卡涩故障
主轴传递弹簧弹性势能的重要组件,由于要传递的冲量极大,因此其机械强度与整体运转流畅度都对分合闸动作具有重要影响。主轴运动通道的轨迹上若出现卡涩情况,将影响整体设备使用寿命,严重时会导致分合闸动作失败。故障设置时,将相扣的A31.5型碟簧组成阻力工装,对弹簧筒内壁应力进而造成形变,从而模拟主轴轻度卡涩故障,如图9所示。
(5)地脚螺栓松动故障
地脚螺栓主要用于将断路器整体固定在地基上,起到稳定断路器的作用。但在多次断路器冲击下,地脚螺栓可能会被振至松动状态,为断路器倾倒等严重事故埋下安全隐患。在保证断路器整体不发生倾倒的前提下,将断路器8个地脚螺栓中的3个用扳手拧松,从而模拟地脚螺栓轻度松动故障,如图10所示。
2.2 声音信号采集及数据集构建
由于断路器的合闸声信号较强,本文将以合闸信号为例,进行样本数据库构建与后续算例验证。LW30-252型SF6高压断路器在合闸时声音为120 dB的宽频信号,因此相应的声学传感器应选择动态响应广、频带范围较宽的传声器。而采集场景四周较为空旷可近似为自由场,综上本文使用14423L自由场声音传感器进行声信号采集,其关键参数如表2所示。另外,为确保记录的信号完整性,相应数字信号采集卡采样频率为200 kHz。

表2 声音传感器技术参数
为了丰富高压断路器声纹特征库,从而提高声纹识别模型的泛化能力,课题组制作了位置可调的声音支架,可根据需要自动调节三个传感器的上下、左右、前后三维位置,每个方向最远距离为340毫米。通过处于不同空间位置的三个声音传感器,可采集到更丰富的声音信息。
采集时用三脚架支撑三维立体声音支架,与操动机构中心高度平齐,在机构的正前方,距离机构外壳前后距离为75厘米、高度为150厘米的位置,三个传感器分别在三维立体支架的最高最前、最左、最右的位置,现场布置情况如图11所示。

图11 声音采集现场图
在实验室条件下施加工频电压进行断路器的声信号采集。高压断路器机械信号经三路声音传感器对故障信息进行采集,每一次合闸分别产生3组信号样本。按2.1节方式分别完成5种故障布置后,对断路器进行分合闸操作与声音信号采集工作。
以正常状态的合闸声纹为例,3个位置采集得到信号波形及包络线如图12所示,包络线平滑数值为100。3通道包络线的互相关性如表3所示,3个通道声信号两两间的皮尔斯相关性系数平均可达到0.893 2,说明不同位置对声纹信号的影响较小,整体基本一致又稍有差异。因此,3个通道数据共同用于模型训练,有助于提升识别模型的泛化性。

表3 声信号包络线相关系数
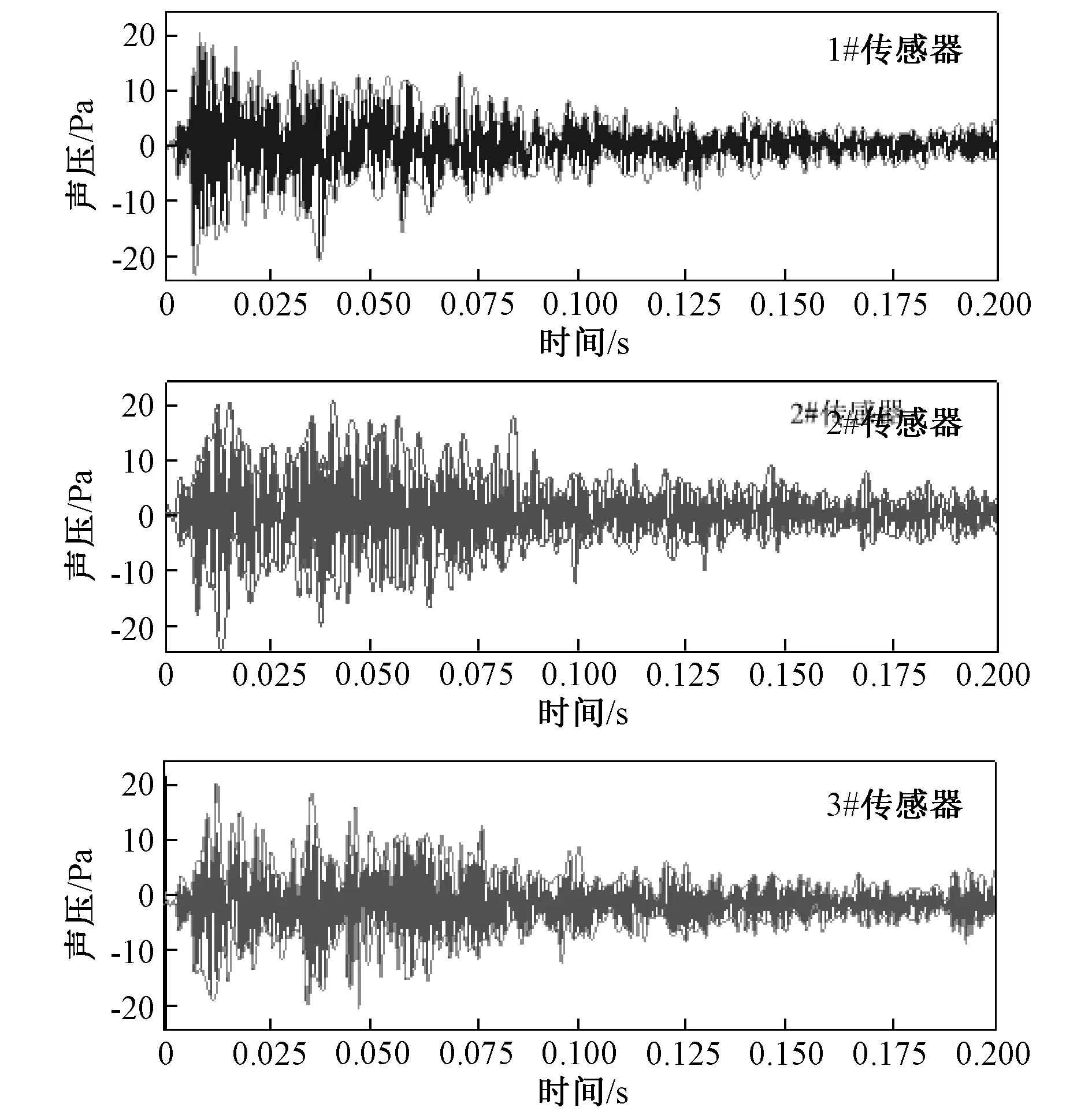
图12 声音采集装置不同位置波形对比
为保证深度学习的有效性,每种故障状态下需要进行200次合闸动作,每次合闸将得到来自3个传感器的3个样本,各故障分别累计600个样本。在进行模型训练时需要对样本进行数据集划分:从3 600例合闸声纹样本中,各类样本中随机抽取500例,共同组成3 000例训练集,其余600例共同组成测试集,最终形成数据集样本分布如表4所示。
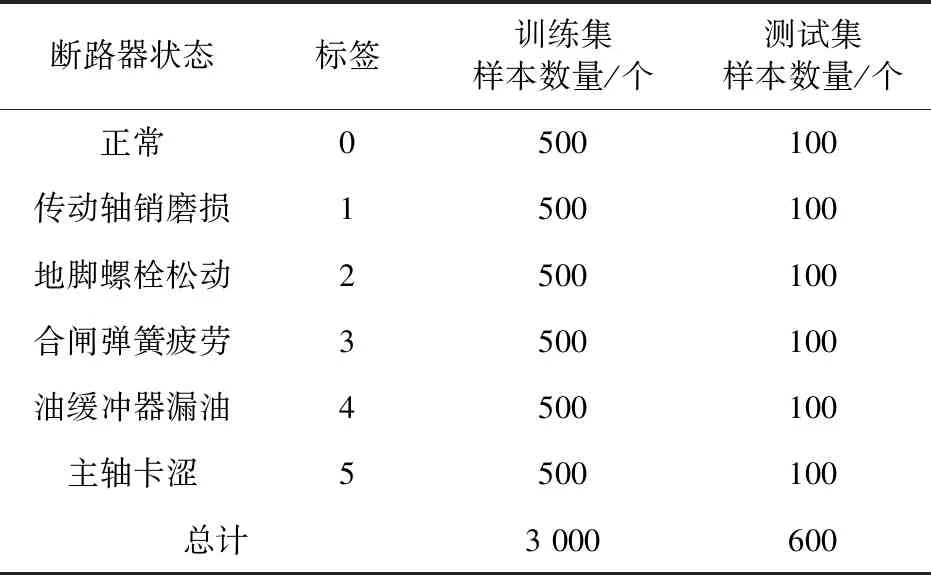
表4 声音数据集样本分布
3 潜伏性机械故障声纹识别
本节将以上文构建的LW30-252高压断路器合闸声纹数据集为基础,进行数据预处理与识别模型训练。
3.1 数据预处理
在进行模型训练与识别前,需要将数据集内数据按1.1、1.2节的方法转化为倒谱特征矩阵。
首先,对0.2 s的原始时域断路器合闸声信号分帧,计算帧长N设为1 024、邻帧交叠长度设为128。由帧长、邻帧交叠长度与样本采样点数可算得本文的声原始时频谱数据尺寸为[44×512]。断路器不同状态下的合闸声信号时频谱图对比如图13所示。由图13中可以看到,5类潜伏性故障的时频谱图具有一定差异,但整体上较为相似,通过人工设计特征量难以区分,因此后续将引入深度神经网络模型作为分类器进行故障识别。

图13 不同状态声信号时频谱图对比
然后,根据合闸声信号时频谱分别计算MFCC、GFCC、PNCC三个特征值,构成倒谱特征矩阵,计算时的fmin与fmax分别设为0 Hz与100 kHz。以正常状态合闸声信号为例,计算结果如图14所示。经过信号降维与特征提取后的倒谱特征矩阵中,矩阵时域分量Z为44,矩阵的频域分量G设为40,声信号的MFCC、GFCCs、PNCC倒谱特征层数为3,即尺寸变为[44×40×3]。倒谱特征矩阵的计算在保留声纹特征的基础上进行了数据压缩,能够提升了后续深度学习的运算效率。
最终,将所有带有标签的倒谱特征矩阵样本按随机顺序输入到CNN网络进行训练。
3.2 参数优化与识别模型结果
为了提高模型性能,研究对MCC-CNN识别模型进行学习率η和批尺寸m进行了优化,整体训练过程按照1.3节中的方法进行迭代。
MCC-CNN识别模型的训练集损失率如图15所示。学习率设置过大将导致不收敛或收敛情况不稳定,学习率设置过小则会导致训练速率过慢。由测试结果可知,当学习率为0.001时,训练集损失率下降较为稳定且训练速度较快。批尺寸不同对模型准确率与训练时间都有一定影响。总训练时间、最终准确率如表5所示,当批尺寸为12与16时准确率达到了100%,综合考虑迭代速度后,认为批尺寸为12时识别模型性能最优。
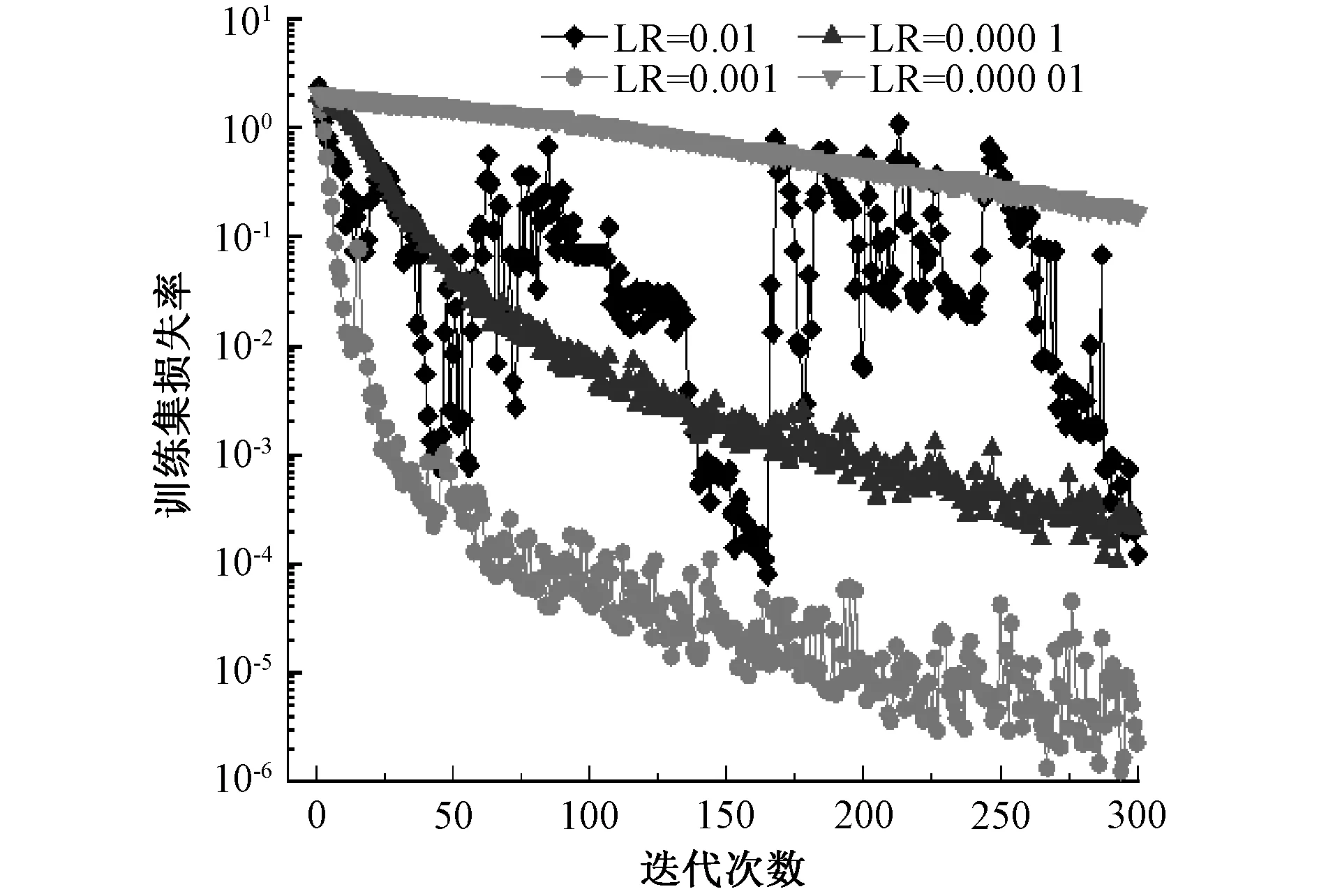
图15 不同学习率对MCC-CNN模型的损失率影响
通过对学习率优化,得到最终的MCC-CNN识别模型,结果如图16所示。MCC-CNN模型在迭代了20次之后,测试集识别准确率即可稳定在100%,迭代100次时损失率可达到10-6左右。

图16 MCC-CNN模型识别准确率与损失率
为进一步对比本文方法的效果,对MCC-CNN、MFCC-CNN、GFCC-CNN、PNCC-CNN以及常规CNN模型的辨识成功率和运算时间进行了对比,结果如表6所示,可见MCC-CNN模型在识别成功率上表现最佳,证明了本文所提出MC-CNN声识别模型的优越性。
与直接使用时频谱图输入CNN网络进行训练和识别的方法相比,MCC-CNN经过了混合倒谱计算的预处理后,数据量计算量大幅下降,样本的数据减少也意味着降低了深度神经网络的识别难度,因此能够提升识别率和降低识别时间。与使用单独某种倒谱系数预处理方法的方法相比,MCC-CNN使用更多类型的倒谱特征能够适应多种潜伏性机械故障声信号,而且从结果上来看,训练得到的MCC-CNN计算速度没有明显劣于数据量更小的单一倒谱系数的方法,提高了准确率的同时计算速度没有明显下降,这是由于Dropout操作剔除了许多冗余的神经元连接,从而优化了计算效率。
4 结 论
本文围绕LW30-252型SF6高压断路器进行了典型机械故障进行声纹识别方法研究,得到了以下结论:
(1)本文所采用的故障设置方法能够模拟断路器的不同潜伏性机械故障状态,在合闸动作的声信号时频谱图中能够体现声信号微弱差异,能够反映潜伏性故障出现时声信号的早期特征,能够为后续MCC-CNN识别模型提供有效支撑。
(2)通过提取声信号的各类倒谱信息并与卷积神经网络结合,能够通过断路器合闸动作声信号进行潜伏性机械故障的状态进行识别,相较于直接将时频谱输入卷积神经网络的方法,本文方法的识别速度与识别准确率都有一定提升。
(3)在潜伏性机械故障声纹诊断中,混合倒谱方法相较于单种倒谱提取方法而言,在识别准确率方面具有更强的优势,但计算速度会略有下降。
