优化学案教学模式 提升数学思维品质

⦿ 甘肃省民乐县第一中学 张 勇

1 提出问题

“学案”教学的优势是不言而喻的,那么是不是所有“学案”都能发挥其积极作用呢?答案自然是否定的.“学案”教学中存在的一些问题是值得反思的.

1.1 是否实现减负增效

实施“学案”的目的之一是提高学生的自主学习能力,然学生的学习能力参差不齐,对于一些学习能力较弱的学生来说,很少有时间和精力完成“学案”,因而使“学案”流于形式.同时,高中生课业负担繁重,学习科目较多,若每门课都增加课前导学内容,势必会给学生带来沉重的负担.因此,如何避免“学案”教学加重学生课业负担是值得教师深思的一个问题.只有找到一个合适的支点才能保证“学案”有序进行,并发挥其重要价值.

1.2 是否符合学生实际

在日常教学中发现,有些“学案”设计并没有联系教学实际从学生的认识水平出发,只是为了“学案”而设计“学案”.学案设计过于形式化,不仅难以激发学习热情,而且会因学案不符合学生最近发展区而使学生产生挫败感,对课堂教学并未产生积极的效果,导学活动因此而失效[1].

1.3 是否客观高效

实施“学案”就是通过问题的引导,充分暴露学生的思维过程,进而结合学生反馈的信息,有针对性地调整教学策略,为提升教学有效性提供宝贵的教学资源.然在实际教学中,部分教师不重视课前导学的检测和分析,仅照本宣科地按照教学计划实施教学活动,使得课前导学与课中教学脱节,长此以往,会减弱学生对学案的关注度,不利于学生自主学习能力的培养.

1.4 是否兼顾全员发展

个体间是存在差异的,那么“学案”设计是否考虑了个体间的差异呢?若“学案”采用“一刀切”的模式,势必会造成一些人吃不饱,一些人又消化不了的现象,这样学生的参与度会大大降低,不利于“以生为主”教学计划的开展,不利于全员发展.

可见,在制定“学案”时,必须以“学生实际”为出发点,使“学案”有明确的目的性、启发性、延伸性、层次性,让每个学生在自主探究和合作讨论中都能有所收获,有所发展,真正成为课堂的主人[2].

2 解决策略

课堂是动态变化的,为此“学案”不能一成不变.教师在教学中应根据学生实际不断优化,进而发挥“学案”的真正价值.笔者以“数列”章节习题课教学为例,浅谈如何实现“学案”的优化,供参考.

2.1 科学指导预习

在数学教学中发现,大多师生认为只有新课才需要细致全面的预习,而复习课或习题课只需多“刷题”.可见,学生在数学学习时还是习惯于“题海”.殊不知,对于复习课和习题课来讲,课前预习尤为重要,这是学生认知体系建构的最佳时机.在本章习题课前,为帮助学生建立函数与数列的联系,丰富解题策略,开拓视野,笔者设计了如下导学内容.

数列与函数息息相关,被视为特殊的函数,结合以下问题你是否能将数列与函数建立联系呢?

(1)若公差d≠0,则等差数列的通项公式可以视为什么函数?

(2)在等差数列的前n项和公式中,若d≠0,它又是什么函数?

(3)联想等比数列,你又有什么发现呢?

这样通过几个简单的问题,促使学生将数列与一次函数、二次函数、指数函数建立联系,为此在解题时除了应用数列的相关性质,还可以利用研究函数的思想方法来研究数列,这无疑给数列问题的求解带来了巨大的便利.其实,很多数学知识间都是存在联系的,然让这些相关或相似的内容建立联系,离不开教师的科学指导.为此,教师要善于从全局或整体上来引导学生进行知识的建构,只有将分散的知识点建立联系,才能形成完善的认知体系,进而便于知识的迁移,提高学生解决问题的能力[3].

2.2 合理安排教学内容

因为本节课是习题课,所以教师在课前精心挑选了5道较为典型的问题让学生独立求解,试图通过学生反馈的问题来实现查缺补漏,强化学习效果.题目如下:

(2)已知数列{an}对任意的p,q∈N*满足ap+q=ap+aq,且a2=-6,那么a10=______.

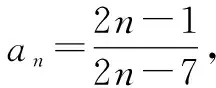
(5)已知数列{an}的通项公式为an=n2+λn(λ∈R),且{an}是递增数列,则λ的取值范围是______.

在“学案”实施中发现,大多学生感觉问题偏难,若全部完成需要较长时间,这样不仅增加了课业负担,而且极易挫伤学生自信心.为此,教师又对题目进行仔细推敲,缩减相似题目.第(3)(4)(5)题都是关于函数单调性的问题,为此仅保留了第(5)题,这样从时间安排上更为合理,不会让学生因任务重而产生厌学情绪.同时,修改后题量适中,学生有较多时间进行思考,有利于自主探究和合作交流活动的开展,有利于思维深刻性的培养.

2.3 开展课前检测

在数学教学中,课前预习流于形式,这与教师的课前检测有一定关系.在传统教学中,预习作业以口头作业为主,学生潜意识里认为这项作业并不重要.同时,部分教师认为教学任务较重,若进行课前检测会占用宝贵的课堂时间,则很可能难以完成教学任务.因为不重视、不检测,才使得数学预习流于形式.学生的自主学习能力并没有因为课前预习而获得较大提升.基于此,教师针对上面“学案”内容,以问题串的方式开展课前检测,进而通过检测效果灵活调整教学计划.

问题1“学案”中的三个问题你是如何求解的?

设计意图:因课前大多学生已经顺利求解,教师引导学生通过口述的方式呈现求解过程,这样有利于培养学生的语言表达能力,为学生合作交流奠定坚实基础.同时,借助求解过程暴露学生的思维,便于教师有针对性地进行引导,从而提高教学有效性.

问题2分析这三个问题,你能找出对应的函数模型吗?

设计意图:与课前导学相呼应,引导学生运用函数的思想来看待数列问题,从而将二者建立联系,完善学生认知体系.

问题3第(5)题有几种求解方法?

设计意图:引导学生从不同角度进行观察和思考,从而找到不同的解法,这样将一题变成了多题,强化了学生对第(5)题的理解.当学生理清了第(5)题的来龙去脉后,教师可以引入“学案”中删除的第(3)题和第(4)题,让学生进行巩固练习,这样通过进一步强化让学生挖掘出问题的本质,善于利用函数的思想来解决数列问题,进而提高解题效率.

问题4在解决以上问题的过程中,应用了哪些数学思想方法?

设计意图:引导学生对解题过程进行反思,进而提炼出有价值的数学思想方法,以便学生更好地掌握问题的本质,提升学习能力.

这样,在问题链的引领下,通过有目的性的合作探究,学生在顺利解题的基础上完成了解题策略的优化.同时,通过对问题本质的挖掘、对数学模型的抽象与数学思想方法的提炼,优化了学生数学思维和数学品质.

2.4 开展拓展训练

众所周知,数列是高中数学的一个教学重点,也是高考必考题型之一.为此,在本章复习时,不能仅限于常规题目的讲解,也要关注知识的拓展延伸,从而借助综合应用提升学生解题信心.

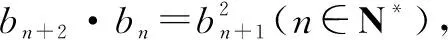
(1)求数列{an}和{bn}的通项公式;

(2)记cn=an·bn,是否存在正整数M,使得对一切n∈N*,cn≤M恒成立?若存在,请求出M的最小值;若不存在,请说明理由.

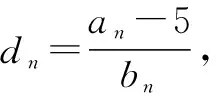
第(1)问的难度不大,为了给问题(2)(3)预留出较多的时间,教师在授课时并没有详细讲解,而是直接给出答案,让学生课后进行完善,通过课后总结归纳完成相关知识的内化.对于后面两问,部分学生容易产生畏难情绪,为此,教师可以带领学生一起探究,通过有效的梳理帮助学生理清问题的来龙去脉,从而帮助学生树立解题信心.同时通过有效的拓展,揭示了知识体系的内在联系和规律,有利于实现知识的迁移,促进学生解题能力的提升.

总之,“学案”设计和实施要坚持“以生为本”,切实从学生实际出发,激发学生参与热情,培养学生良好的数学思维品质,真正实现“减负增效”.