坐标伸缩变换视角下的椭圆探究

⦿ 安徽省蚌埠市第四中学 穆 颖

1 起因

蚌埠市2022届高三年级第二次教学质量检查考试理科卷第20题考查了椭圆问题,原试题如下:

“工艺折纸”是一种把纸张折成各种不同形状物品的艺术活动,在我国源远流长,某些折纸活动蕴含丰富的教学内容.例如,用一张圆形纸片,按如下步骤折纸(如图1):

图1

步骤1:设圆心是E,在圆内异于圆心处取一点,标记为F;

步骤2:把纸片折叠,使圆周正好通过点F;

步骤3:把纸片展开,并留下一道折痕;

步骤4:不停重复步骤2和3,就能得到越来越多的折痕(如图2).

图2

已知这些折痕所围成的图形是一个椭圆.若取半径为4的圆形纸片,设定点F到圆心E的距离为2,按上述方法折纸.

(1)以点F,E所在的直线为x轴,线段EF的中垂线为y轴,建立平面直角坐标系,求折痕所围成的椭圆C(即图1中M点的轨迹)的标准方程.

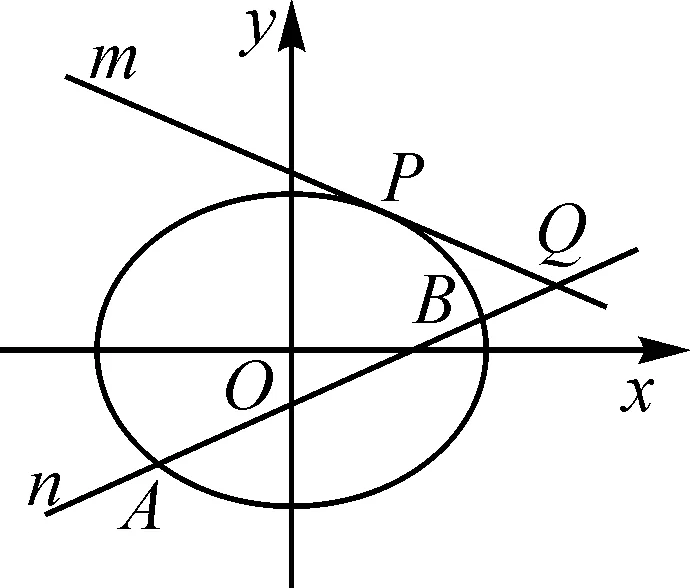
图3

证明:|AQ|,|PQ|,|BQ|成等比数列.

参考答案如下:

由直线m与椭圆C相切于点P,可知

Δ=s2-4(s2-3)=0.

又s>0,所以解得s=2.

由x2-2x+1=0,解得x=1.

即|PQ|2=|AQ|·|BQ|.

故|AQ|,|PQ|,|BQ|成等比数列.

2 分析

在第(2)问的证明中,为了求出|AQ|,|PQ|,|BQ|的表达式,需要多次把直线方程和椭圆方程、直线与直线方程联立,再使用弦长公式,运算量着实比较大.我们可否另辟蹊径,找到一种简捷的处理方法呢?在本题中直线PQ是椭圆C的切线,直线AB是椭圆C的割线.在研究圆时,已学习过圆的切割线定理.若把椭圆伸缩变换成圆,再借助圆的切割线定理,是不是就可以得证了呢?变换中还需要关注变换前两点间距离与变换后两点间距离是否成比例.

3 探究

在人教A版数学选修4-4中,学习了坐标伸缩变换,伸缩变换的常用性质主要有以下几点:

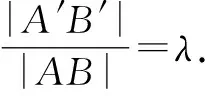
性质2若坐标伸缩变换前直线与曲线相切(相交、相离),则坐标伸缩变换后直线与曲线依然相切(相交、相离).

性质4若坐标伸缩变换前图形的面积为S,则坐标伸缩变换后图形的面积S′=λμS.

4 巩固练习

无独有偶,在人教版数学选修4-4第38页有如下一道例题:

如图4所示,AB,CD是中心为点O的椭圆的两条相交弦,交点为P,两弦AB,CD与椭圆长轴的夹角分别为∠1,∠2,且∠1=∠2,求证:|PA|·|PB|=|PC|·|PD|.

图4

课本通过设直线的参数方程并与椭圆方程联立,借助参数t的几何意义,推出|PA|·|PB|=|PC|·|PD|,这样需要进行大量的纯字母运算.那么,可否找到一种快捷的解法呢?在本题中线段AB,CD都是椭圆C的弦.在研究圆时,已学习过圆的相交弦定理.若把椭圆伸缩变换成圆,再借助此定理,就可以得证.

图5

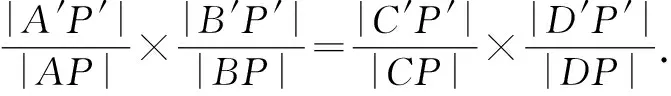
由圆的相交弦定理,知|A′P′|·|B′P′|=|C′P′|·|D′P′|,故|PA|·|PB|=|PC|·|PD|.

5 结束语

从以上的解答中,我们或许会惊叹:这简直不像是解析几何题了,几乎没有计算量!是的,坐标伸缩变换可将椭圆转换为圆,而圆具有椭圆不具备的许多特殊性质,并且和圆有关的问题还可以借助初中平面几何知识来解答,从而避免繁杂冗长的计算,提高解题效率.