UCM协同理论控制机制及应用的研究进展

杨宗青 ，米 靖，周松芳，万祥林，张强峰

（1. 湖南师范大学 体育学院，湖南 长沙 410012；2. 湖南师范大学 体适能与运动康复湖南省重点实验室，湖南 长沙 410012；3. 湖南师范大学 湖南省体育公共服务研究基地，湖南 长沙 410012；4. 北京体育大学，北京 100084；5. 广州铁路职业技术学院，广东 广州 510430）

如何利用人类运动系统中多个自由度（degree of freedom）实现特定的运动目标？这是经典的“自由度问题”，也被称为“Bernstein 问题”。该问题自Bernstein（1967）提出以来，成为运动控制领域中的一个核心议题。运动系统（肢体、关节、肌肉）在许多任务中是冗余的，即运动冗余（Gelfand et al.， 1998）。也就是说，通常有多个关节或肌肉可用于控制一组任务变量，如控制手在空间中的位置或方向。运动冗余会产生运动变异。研究者起初认为运动变异是运动冗余系统在运动过程中产生的“噪声”，会影响任务目标的准确性，但从技能学习的过程看，运动变异被认为是一种“有目的的探索过程”（Davids et al.，2005），也是人体运动系统的控制策略（王爱文 等，2017）。Bernstein（1947）发现，当铁匠多次用铁锤敲击凿子时，单个关节的轨迹变异大于铁锤的轨迹变异，因此提出了“运动协同”的观点，即“协同层面”在其多层次运动控制系统中有2 个主要功能：1）负责将众多元素（如肌肉）组合在一起，从而缓解运动冗余问题（减少自由度），以加强运动控制；2）确保运动的动态稳定性，这对于控制不可预测的、变化的外力和内在的身体状态至关重要。前一个功能后来发展为协同的第一种定义，即共享模式的协同，加之最初主要是通过肌电图进行相关问题的分析，因此称之为“肌肉协同理论”（Latash et al.， 2015）；第二个功能则在50多年后成为非受控流形（uncontrolled manifold，UCM）假说的基础，发展为协同的第二种定义，即误差补偿模式的协同（Latash et al.， 2021）。因为该协同的分析指标是基于UCM计算得出，因此称之为“UCM 协同”（Martin et al.，2009）。

如今，运动协同已经成为动作控制领域中无法回避的问题。肌肉协同理论提出的模块化控制理念，能够对原始变量的控制起到降维的作用，缓解了运动冗余（Latash et al.， 2015）。然而肌肉协同理论并没有完全解决运动冗余的问题（Latash et al.， 2021）。有关肌肉协同是在中枢神经系统中编码，还是由于任务约束而被激活的问题，仍存在争议（杨毅等，2020）。基于肌肉协同作用的神经表征在运动皮质区域中的证据寥寥无几，鲜有研究直接将人类初级运动区域内的神经反应与基于协同的肌肉控制或皮层所规划的降维策略联系起来。肌肉协同理论也未能回应外周约束相对于中枢命令在生成肢体耦合运动方面的相对贡献问题。

UCM 是由Scholz 等（1999）提出的一种关于动作控制的革命性理念，并有其严谨、系统的分析计算方法。其初衷是为了分解冗余运动系统中的变异，以及判断特定任务中哪些变量由神经系统重点控制。UCM 假说极大地促进了人们对运动协同的理解和分析，对研究与运动科学和神经科学相关的协同有着独特的贡献。近年来，UCM协同理论在动作行为领域的应用日趋增多，国内学者将“uncontrolled manifold”翻译为“无控制流形”或“非控制流形”，但鉴于这一概念所表达的确切含义是“在平行于UCM 的空间中，基本变量的组合不受中枢神经系统的控制”，有被动的意味，因此将UCM 翻译为“非受控流形”可能更为贴切。那么，UCM 协同的基本理念是什么？其能否解决运动冗余的问题？相比肌肉协同理论有何独到之处？UCM 协同的分析过程和评价指标有哪些？其存在的证据及其神经控制机制是什么？UCM 协同具体应用在哪些领域，解决了哪些问题？本研究围绕这些问题进行综述，以期深刻认知和理解UCM 协同理论，并展望该理论在未来研究和应用中的发展趋势。

1 UCM协同的基本理念以及与其他协同或控制理论的比较

1.1 UCM协同的基本理念

UCM 协同具有误差补偿特征，即基本变量之间可相互补偿因变异而产生的误差，从而保持任务变量或结果变量的稳定输出（Reisman et al.，2003），这种协同概念与结果稳定性联系了起来。根据这一定义，协同是指在执行特定任务的过程中，保证重要任务变量稳定的神经组织。该定义认为运动冗余并不会成为中枢神经系统的负担，而是作为一种丰富的资源，允许各基本变量（自由度）之间进行灵活的变异和配合，在同时应对其他任务或外界扰动时，仍能保持动作结果的稳定（Prilutsky et al.， 2002）。这是UCM 意义上的协同相对于抽象地量化共享模式协同（独立于功能任务）的一个特殊优势（Vaz et al.， 2019）。因此，Gelfand 等（1998）提出了富余原则（principle of abundance）假设，即所有层次的自由度总是参与所有的任务，以确保结果的稳定性和过程的灵活性。过去所提出的自由度冗余（redundancy）的概念隐含着自由度过多的意味，而自由度富余（abundance）的概念则有越多越好的含义。

1.2 UCM协同与肌肉协同理论的区别

肌肉协同理论是指原始变量中，某组变量（如一组肌肉）激活水平平行变化，并由一个协同元控制，该协同元所控制的变量的激活或运动程度成固定比例，即在这些变量之间存在“协同”或特定运动（或激活）“模式”（Krishnamoorthy et al.，2003）。这种通过对原始变量进行矩阵分解（如主成分分析法、非负矩阵分解法）所得出的运动协同模式是一种运动元素之间共享活动的模式，简称为“共享模式”（sharing patterns），其通过降维实现对原始变量的间接控制，缓解运动冗余。共享模式的协同是抽象的，着重于动作过程的稳定，是一种模块化控制。但这种协同的概念却难以解释这样的情形：在有外界干扰的情况下，保持动作结果稳定的同时，还能使运动具有较高程度的适应性和灵活性（Latash et al.， 2007）。

UCM 协同与肌肉协同理论虽然都溯源于Bernstein（1947）的“运动协同”理念，且均有客观证据支撑（表1），但存在本质的区别。具体体现在：1）肌肉协同理论是一种共享模式（模块化）的协同，即某运动时间段（点）各基本变量之间固定的耦合模式，而UCM 协同是误差补偿模式的协同，指的是各基本变量之间的相互补偿，基本变量的自发波动会对任务变量或结果变量产生影响，误差补偿模式就是将这种影响最小化（Reisman et al.，2003）。2）肌肉协同理论致力于通过降维缓解运动冗余，而UCM 协同则将运动冗余作为一种丰富的资源加以充分利用。3）肌肉协同理论偏重于动作过程的稳定，而UCM 协同强调的是动作结果的动态稳定性控制（Vaz et al.， 2019）。4）肌肉协同理论是抽象的，UCM 协同是针对具体任务的特定组织，服务于具体的任务目标（Latash et al.， 2007）。另外需要说明的是，两种理论主要是理念上的区别，二者都可以分析肌肉、关节、肢体等冗余系统中的协同关系。

表1 3种理论假说的比较Table 1 Comparison of Three Theoretical Hypotheses

1.3 UCM协同与对照设置假说的联系

UCM 协同与对照设置假说存在天然的联系（Latash，2010a）。二者均基于动态系统理论，其基本理念一致，都认为中枢神经系统动态地控制动作，但不是决定运动结果的唯一因素，动作结果还取决于机体内部之间，以及机体与环境之间的相互作用（表1）。

对照设置假说（referent configuration hypothesis）是平衡点假说（equilibrium point hypothesis）的一种发展和推广。在过去的50 年里，平衡点假说已经从描述简单的单关节系统控制的假说，发展为能解释复杂运动（如多关节运动）的理论（Latash et al.，2010）。平衡点假说的主要思想是通过肌肉激活阈值的改变，对具体运动进行神经控制，因此也被称为阈值控制理论（threshold control theory）（Feldman et al.， 2009）。根据对照设置假说，神经控制器设定了一个身体的对照设置，在这个设置下，所有肌肉通过拉伸反射处于激活阈值。实际设置和对照设置之间的差异诱发肌肉活动。（Latash， 2010a）。

两种假说对同样的行为所描述的角度不同：UCM 协同描述了元素（基本变量）输出的协变，而对照设置假说则深入至神经系统的控制（Latash， 2010a），两者相结合能起到相辅相成的效果。已有研究结合对照设置假说阐述UCM 协同产生的机制（Latash， 2010a），还有研究将UCM协同与对照设置假说统一起来，进行数学建模，有效解析了UCM 协同产生的神经机制（Martin et al.， 2009， 2019）。

2 UCM协同的分析过程及评价指标

常用于评价UCM 协同的指标有4 个：VUCM（任务无关变异）、VORT（任务相关变异）、ΔV（协同指数）以及预期协同调整（anticipatory synergy adjustments）。本文以在二维平面上做指向运动的任务为例，阐述UCM 的分析过程（评价指标的计算过程）。任务要求在多次重复的动作中尽量指向并触及同一个位置的点（图1）。

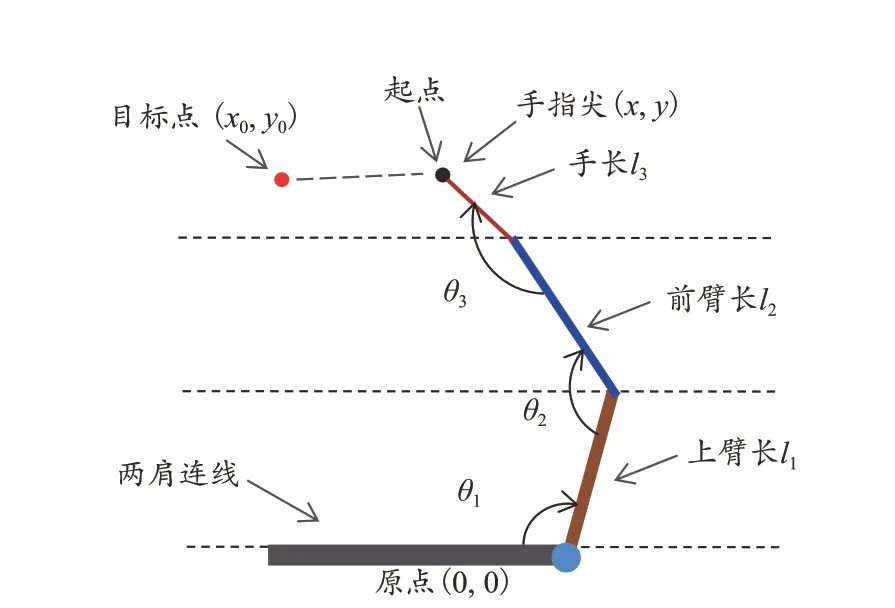
图1 手在桌面上做指向运动的示意图Figure 1. Schematic Diagram of Pointing Movement of Hand on the Desktop

2.1 建立基本变量和任务变量的函数关系

在二维平面（桌面）上做指向运动时（图1），上臂只允许在水平面内运动，肩、肘、腕关节分别只允许一个自由度运动（肩水平内收外展、肘屈伸、腕内收和外展），在指向运动结束瞬间，这些关节角度组成基本变量并张成一个角度空间（为简化，只分析指向任务结束瞬间手臂的姿势）。然后将指向运动结束时手指尖的坐标位置（x，y）称为任务变量（或结果变量、受控变量）。原点位置（0，0）为两肩连线和上臂的交点。

基于几何学，任务变量与基本变量之间形成一个函数关系：(x，y) =f(θ1，θ2，θ3)，表达式如下：

需注意的是，该分析采用的基本变量是关节角度（Monaco et al.， 2018），而非Scholz 等（1999）的分析中所采用的环节角度（各环节相对于水平线所形成的角度）。Sternad 等（2010）研究发现，采用2 种不同的角度，计算所得出的结果也不同。Scholz 等（2014）分析认为，用环节角度表示的基本变量之间不能相互独立，而是相互影响的，这就人为地使各基本变量之间产生协变，导致结果失真。解决该问题的方法是采用关节角度定义各基本变量，保持基本变量之间的相互独立，虽然在计算上比采用环节角度更复杂，但有利于保证计算结果的真实性（Scholz et al.，2014；Sternad et al.，2010）。

当每次指向运动结束，手指尖处于同一位置，比如准确指向固定的目标点（x0，y0）时，相对应的关节角度的集合即为以上方程的解集。其中θ1、θ2、θ3分别表示肩的水平内收外展角、肘的屈伸角、腕的内收外展角，以弧度表示，假设这3 个角度的取值范围都为（0，π）。l1、l2、l3分别表示上臂、前臂和手的长度，其长度分别为l1=1.0，l2=0.8，l3=0.3（Scholz et al.，1999）。理论上讲，这些关节角度之间可以有无限种组合，因为效应系统关于任务的描述是冗余的：3 个关节（空间维度n=3）控制着手末端位置的2 个元素（x，y）（空间维度d=2）。事实上，这些关节角度的集合形成了一个一维（n-d=1）的流形，称之为UCM，因为在这个流形里，对关节组合的控制是不必要的，它们并不影响任务变量的位置，在这个空间中各基本变量的所有变异都可归类为VUCM（Scholz et al.，1999）。

2.2 对流形UCM进行线性化

由于手指尖运动的几何模型是非线性的，而UCM 是一个曲线空间，需要对其进行线性化，这样一个线性化的UCM 定义了2 个子空间，即非受控子空间（该空间中发生的关节角度变异即为VUCM）和其正交补空间（该空间中发生的变异即为VORT）（Scholzet al.，1999）。线性化首先需要确定一个对照设置，对照设置（θ01，θ02，θ03）可选择在指向运动结束时多次重复动作的平均关节角度（可根据试验数据求得）。线性化则是基于几何模型在对照设置处的雅可比矩阵（手指尖坐标在平均关节角度θ0处对关节角度的偏导数），即：

另外，对于一些解析计算很复杂的情况，可通过建立基本变量与任务变量的线性回归来估算雅可比矩阵（Freitas et al.，2010）。例如，要建立肌电激发模式（基本变量）与足底压力中心位置（任务变量）的雅可比矩阵，只能通过实测数据的线性回归来估算（Krishnamoorthy et al.，2003）。

雅可比矩阵的零空间记为ε，是一个基向量，为线性化的UCM，即：

本例中的基向量ε=［θ1-θ01，θ2-θ02，θ3-θ03］T，是一维的列向量（n-d=1）。基向量ε，即等式（3）中所有θ1、θ2、θ3的解集，张成了线性化的UCM（零空间）（图2）：θ1、θ2、θ3为3 个关节角度，实曲线表示一个恒定的手的末端点的位置（x=-0.5，y=0.8）所对应的一组关节角度（各环节的相对长度，上臂l1=1.0，前臂l2=0.8，手l3=0.3）［同Scholz 等（1999）的参数设置］，实曲线即为一维流形UCM（一维流形为曲线，二维流形为曲面，依此类推）。虚直线为实曲线在平均关节角度θ0（θ01= 2.782，θ02= 1.51，θ03= 0.805 6）处的切线，虚直线即为在θ0处线性近似化的流形UCM。基向量ε张成的空间，平行于该流形UCM。

图2 三关节角度空间的UCM及其线性化的UCMFigure 2. UCM of Space Formed by Three Joint Angles and Its Linearized UCM

2.3 分解基本变量中变异

计算每次试验的各关节角度分别与其平均关节角度（根据所有试验计算）的差值，3 个关节的差值，即3 个自由度组成一个包含3 个元素的列向量Δθj（j表示第j次试验）（Scholz et al.，1999）。

将Δθj向量分解为2 个空间（投影到2 个空间）：与零空间平行的空间［Δθ׀׀(j)］和与零空间垂直的空间［Δθ┴(j)］。计算如下：

其中εk为零空间ε的第k列，共n-d列，n为基本变量空间维度，d为结果变量空间维度，本例中n-d=1，因此零空间ε只有1 列。

2.4 VUCM、VORT和ΔV

2 个投影在总试验次数中的方差分别为：

M为总试验的次数，每一次试验用j表示。

一般认为，如果ΔV为正，说明存在UCM 协同效应。VORT的值越小，表明在做指向运动的过程中，任务变量受神经系统控制的程度越大，完成任务的准确性越高。VUCM虽被称为任务无关变量，但并非与任务变量没有关系（Latash，2010a），VUCM本身不会改变任务变量，但提供了系统的灵活性，体现在：1）可以使用相同的基本变量执行其他任务；2）可以应对被施加在其中一个（或几个）基本变量上的意外扰动；3）有证据表明，有目的地增加VUCM可能与允许系统在异常条件或不确定条件下探索各种解决方案有关（Freitas et al.， 2009；Yang et al.， 2007）。

当指向一个目标时，外界的瞬时扰动或多或少地对各关节及手指的运动产生影响。如果手指仍能准确触及目标，就表明产生了UCM 协同或运动等效（motor equivalence）（Scholz et al.，2014）。在量化有外界干扰的UCM 协同时，可先进行一组无干扰的测试，确定基本变量和任务变量的关系，并求出雅可比矩阵，然后计算各基本变量在若干次测试中所得的平均值（无干扰的情形），并在该平均值处求得零空间。接着，计算各基本变量的实际值（有干扰的情形）与其平均值（无干扰的情形）的差值，再对各基本变量的变异进行分解（计算过程如2.3、2.4 所述）。有研究采用该方法计算发现，在面对突然的外界扰动时，有舞蹈经验者与普通人群相比，控制身体重心的协同能力显著更强（Koh et al.，2020；Wang et al.，2019）。

2.5 预期协同调整

虽然运动稳定性在大多数任务中至关重要，但有时也可能会适得其反。例如，如果个体想要快速改变一个变量（以切换到不同的任务），那么通过强大的协同来确保该变量的高稳定性并不是神经系统的最佳策略。稳定性和灵活性（敏捷性）之间存在此消彼长的关系。一些研究表明，中枢神经系统能对运动协同进行调整，为快速切换动作做准备（Olafsdottir et al.， 2005； Shim et al.， 2005；Zhou et al.， 2013）。在快速切换任务前的200～300 ms，ΔV（总方差中VUCM的相对数量）显著下降（图3），这就是预期协同调整（Latash et al.，2015）。如果说ΔV表示在执行任务时的稳定性，预期协同调整则表示转换任务时的敏捷性。从一个任务转换至另一个任务时，需首先破坏原有的协同作用，才能重建新的协同作用。这个破坏—重建的过程持续时间越短，即预期协同调整值越小，表明中枢神经系统越敏捷和灵活（Latash et al.，2015）。

图3 预期协同调整（Latash et al.， 2015）Figure 3. Anticipatory Synergy Adjustments （Latash et al.， 2015）

3 UCM协同的神经控制部位和控制模型

在UCM 理念创立之前，绝大多数有关运动控制的实验测试使用的是非冗余运动（对运动进行人为约束），这与实际的运动控制相差甚远，自UCM 理念出现之后，运动科学家才开始系统地利用运动装置固有的冗余来分析运动是如何被控制的（Martin et al.，2009）。

3.1 UCM协同的神经控制部位

UCM 协同是一种动态稳定性的协同（Latash et al.，2007）。动态稳定性在中枢神经系统中是普遍存在的。它是神经元网络生物物理学的一个基本特征，神经元网络能在外部或内部扰动后恢复到原来的状态（Wilson，1999）。Paus 等（1993）的研究发现，前扣带运动皮质能通过促进恰当的运动反应和（或）抑制不恰当的运动反应参与对运动的控制。那么，能否由此推断UCM 协同是由大脑皮质控制的？以下几个研究提供了否定回答。

在音节产生的任务中，人类下颚的意外扰动会导致远离扰动部位的发音器官发生代偿性活动，使音节仍然正常产生（Kelso et al.， 1984）。需注意的是，该代偿性活动的反应潜伏期约为20 ms，大脑皮质根本来不及对其进行控制。关于脊蛙的擦拭反射研究表明，即使其中一个关节的运动意外受阻，或者一个远端环节承受了重负荷，青蛙也能准确地擦拭其背部或前肢的刺激物（Berkinblit et al.，1986）。一项涉及躯干运动的“指向触及”任务研究发现，当躯干意外受到约束时，在躯干停止运动后40 ms内，可以检测到手臂关节间协调的变化，从而保持手指向目标点的运动（Rossi et al.， 2002）。这些反应不太可能是由皮质通路引起的。因此有研究推测协同的误差补偿特征可能仅依赖于脊髓和脑干通路（Reisman et al.，2003）。

近年来对神经系统疾病患者的研究为理解运动稳定性的神经生理机制作出了重要贡献。小脑损伤患者的单关节屈伸功能未受影响，但却无法正常完成多关节的复合运动，因此推断小脑是多关节复杂运动的重要协调控制部位（刘宇，2010）。大量研究表明，帕金森（Ambike et al.，2021）、多发性硬化症（Jo et al.，2016b）、橄榄体脑桥小脑萎缩（Park et al.， 2013b）、脊髓小脑变性（Asaka et al.，2011）患者在执行动作时的ΔV存在不同程度的降低，且帕金森患者在预期协同调整上，其ΔV降低的幅度更小（Jo et al.，2015），并同时表现出调整时间上的延迟（Falaki et al.，2018；Park et al.，2012）。这些病症的共同点是与基底神经节或小脑等皮质下环路的病变有关。

与基底节和小脑的病变不同，中风幸存者在指向任务（Reisman et al.， 2003）和手指力量产生任务（Jo et al.，2016a）中的ΔV没有出现变化，这表明中风幸存者保留了结合基本变量以稳定目标任务的协同能力。Reisman 等（2003）研究了8 名中风幸存者［（60.6±4.7）岁］的运动能力，被试曾患过1 次皮质中风，导致手臂功能中度受损。尽管脑患侧的对侧手臂和同侧手臂相比，在整体运动模式（共享模式的协同）上存在差异，绝对指向误差更大，运动时间也更长，但其多关节ΔV相似。此外，中风患者与同龄的健康对照组相比，其ΔV也未见显著性差异。

对神经系统不同病理学的UCM 研究结果表明，稳定性控制与神经系统的不同功能有关：整体运动模式受皮质脊髓束损伤的影响更大，有证据表明，中风患者大肌群的肌肉独立性和共收缩性降低，反映了下行神经通路的部分中断，并与运动功能缺陷相关，但稳定整体运动模式的UCM 协同能力更多地受到皮层下通路功能障碍的影响，大部分中风患者不存在这个问题（Latash et al.，2015；Park et al.，2012， 2013b）。

综合以上证据，研究者认为，与UCM 协同存在密切联系的是皮层下结构（如基底神经节和小脑），而不是大脑皮层（Latash et al.，2015）。这与Houk（2005）的理论比较吻合，该理论认为大脑通过分布式处理模块控制运动，2 个解剖学定义的分布式处理模块（联合成环路的神经元结构）存在不同的功能：1）连接基底神经节的环路，负责行为的选择和启动；2）连接小脑的环路，负责行为的放大和细化。

3.2 UCM协同的控制模型

尽管有大量的实验研究支持UCM 协同，但只有少数研究尝试对如何实施这种控制方法进行建模和解释（Goodman et al.，2006）。目前用来解释UCM 协同机制或假说的有最小干预原则（minimal intervention principle）对照设置机制和中枢反向耦合（central back-coupling）机制。研究者在这些机制或假说的基础上，建立了旨在反映UCM 协同特征的数学模型，主要分为3 类：第一类是以最小干预原则为基础的反馈控制模型；第二类不是严格意义上的数学模型，既不完全属于反馈控制，也不完全属于前馈控制，重点从对照设置机制的角度分析UCM 协同特征；第三类则是结合了中枢反向耦合机制和对照设置机制的前馈控制模型。

3.2.1 反馈控制模型（最小干预原则）

Todorov 等（2002）提出了动作技能的最优反馈控制原理，该原理遵循“最小干预原则”，即只有当偏离平均轨迹的运动偏差干扰任务结果时才会被纠正。通过只纠正与任务相关的误差，该模型将噪声的潜在影响降至最低（Scott， 2002），因此能产生基本变量变异的UCM 结构。Todorov 等（2002）解释了最小干预原则能够成立的原因：最优反馈控制器并没有从纠正任务无关偏差中获得益处，因为它唯一需要控制的是任务结果，而这种偏差不会干扰任务结果。此外，产生的校正控制信号也会产生噪声，会增加控制过程的复杂性。中枢神经系统不会控制每个关节（环节）的精确运动，只有当关节（环节）的运动使任务偏离预定目标时，系统才会施加控制（McCaskey et al.，2018）。

Reimann 等（2017）针对人体静止站立时重心稳定性的控制，建立了4 种不同的反馈控制模型，即近端关节共收缩的踝关节策略（A 模型）、近端关节局部反馈控制的踝关节策略（B 模型）、多关节协调的踝关节策略（C 模型）、多关节协调的分布式策略（D 模型）。将模型所模拟的数据与实验测试数据进行对比发现，主动协调不同关节间肌肉激活的控制律（C 和D 模型）产生了正确的变异模式（方差模式），而单独控制每个关节的控制律（A 和B 模型）则未能产生。这说明UCM 协同是中枢神经系统在关节之间主动协调的结果。C 和D 模型同样遵循最小干预原则，但与Todorov 等（2002）所假设的动作控制的“最优反馈控制”并不完全一致。在Reimann 等（2017）的研究中，控制器的最优性似乎并不重要。该研究假设D 模型是最优的，因为其产生所期望的任务反馈，能在关节角度变异最小的情况下稳定空间中的身体。相比之下，C 模型产生的关节空间变异更大。然而，这2 种模式产生的协方差结构非常相似。这一结果支持了Loeb（2012）所提出的观点：满足于“足够好”的解决方案比满足于最佳方案更有利于生物系统。从生物系统的整体角度看，满足于“最小干预原则”的解决方案不止一个，在不同的情境下，不同的方案各有优劣。

3.2.2 对照设置模型（对照设置机制）

大多数现有动作协同模型的共同缺点是使用外显变量［如肌肉力、关节力矩、关节角（速度）］的语言，而不是试图将外显变量与神经控制变量的变化联系起来。这隐含着该语言足以代表中枢神经系统控制策略的假设，但外显变量表现出的协同可能并不是因为神经控制器组织了一组基本变量之间的协变，而是由身体对照设置的基本控制机制所致的（Latash，2010a），这与Reimann 等（2017）提出的“UCM 协同是中枢神经系统在关节之间主动协调的结果”的观点有所不同，前者偏向于机体与外部环境的相互作用，后者强调神经系统的控制作用。

Latash（2010a）认为，根据对照设置机制，基本变量之间由2 种类型的协变模式构成，一种是由对照设置的控制引起的，另一种不是由这种控制机制决定的。Latash（2010a）以棱镜式抓法抓握物体为例进行了说明（图4）。假设大拇指产生的法向力为F1，4 个手指产生的法向合力为F2，每个手指（食指、中指、无名指、小拇指）的法向力分别为FⅠ、FM、FR、FL。

图4 设置APREF产生手指对物体的主动握力Figure 4. Setting a Value of APREF Produces Active Force of the Fingers against Object

中枢控制器设置对照孔径（referent aperture，APREF）。实际孔径（actual aperture，APACT）和APREF之间的差异（APACT＞APREF）引起神经元产生动作电位，导致大拇指和其他四指产生相向移动，直至APACT=APREF，如果手指无法移动，则会对物体的壁面产生主动握力（图4）。这种控制模式总是导致2 个相反的力相等（F1＋F2=0），如果APREF偏离中心（图4B），则可能在不同的空间位置实现。由于F1＋F2=0是一个含有2 个未知量的方程，一个方程含有2 个未知量，因此理论上会产生运动冗余，会导致拇指产生的法向力和四指产生的法向合力之间的协变，以将总的合力稳定在接近0 的水平，即限制了VORT的大小，以保证尽可能准确完成目标任务。根据对照设置假说，这种协变是由所设置的APREF引起的。有趣的是，如果2 个相对的效应器（分别产生F1和F2）属于2 个参与者，则此控制方法将不可用，因为2 个参与者必须为每个效应器设置对照坐标，而不是APREF值，这导致在横向方向稳定合力的ΔV显著降低（Gorniak et al.，2009）。

在固定的APREF下，单个手指对照位置的协变机制较为复杂。4 个手指可分为4 个对照位置，即Ri（i=食指、中指、无名指和小指），满足给定APREF的Ri组合有无限个，即F2=FⅠ＋FM＋FR＋FL。对这些组合的变化并不需要施加任何限制，因此这是不受神经控制机制决定的协变模式（Latash，2010a）。

上述案例通过对照设置假说的神经控制原理，对UCM 协同进行了更深刻的剖析，即VUCM至少可分为2 类：一类由对照设置（中枢机制）控制，以限制VORT，保证目标任务的准确完成；另一类则不需通过对照设置控制，这类协同提高了任务过程的灵活性和抵抗外界干扰的能力。

3.2.3 前馈控制模型（中枢反向耦合机制）

对于一些比较慢速的动作，有足够的延迟时间进行反馈。但对于一些快速的动作（如反馈时间＜40 ms），在动作完成的过程中，高级中枢来不及参与反馈。但在这些快速的动作中，仍然表现出UCM 协同效应，这显然用反馈控制理论无法解释。Latash 等（2005）提出了中枢反向耦合（central back-coupling）机制的假说，该机制的神经基础是闰绍细胞所构成的回返式抑制。

3.2.3.1 结合中枢反向耦合机制的前馈控制模型

Latash 等（2005）以4 个手指的协同用力为例，构造了中枢反向耦合模型（图5）。命令信号（A 级）分布在4 个神经元上，产生特定的共享模式，用公式表达为：S（t）=［si，sm，sr，sl］，其中矩阵S为A 级神经元总的兴奋值输出，t 表示时间，即S会随时间t而变化，下标表示单个手指（分别为食指、中指、无名指、小拇指），其兴奋的比例分别为0.31、0.29、0.21、0.19，使4 个手指总的兴奋值保持在1.00。

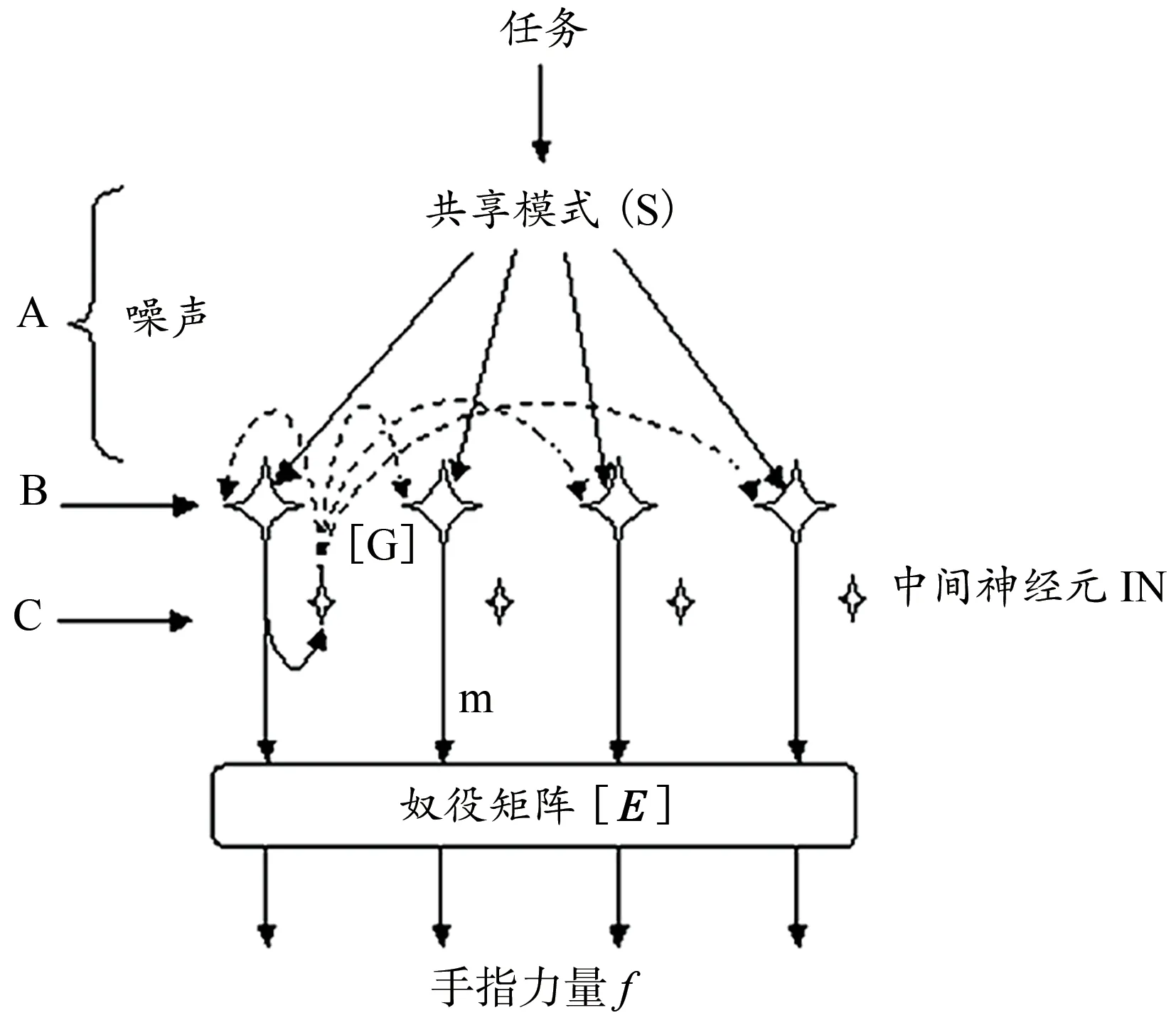
图5 构成中枢反向耦合模型基础的网络（Latash et al.，2005）Figure 5. The Network of the Central Back-CouplingModel（Latash et al.，2005）

假定发出信号的同时会产生噪声，导致单个神经元（B 级）的兴奋输入随机偏离共享模式所规定的值，SB（t）=S（t）＋N（t），其中SB为A 级神经元经噪声干扰后输入至B级神经元的信号，N=［ni，nm，nr，nl］是噪声向量。每个B 级神经元在输出下行兴奋性信号的同时，还将兴奋性信号投射至中间神经元（C 级有4 个中间神经元），然后中间神经元将抑制性信号投射回所有4 个B 级神经元，即抑制性投射（图5 中的虚线箭头），由此构成神经元的反向耦合机制。这些反向耦合回路的特点是增益（由增益矩阵G产生）、时间延迟（Δt），并且由阈值控制。因此，至B 级神经元的总输入量BⅠN（t） =SB（t）＋［G］m（t-Δt），其中m（t）是B 级神经元的输出，Δt是反向耦合的时间延迟。除了投射到C 级中间神经元上，B 级神经元的输出还通过手指之间的奴役矩阵［E］进行转换，从而产生手指力f=［E］m，通过这一系列过程，在神经控制层面上表现出UCM 协同特征，保持了四指总力的稳定（Latash et al.，2005）。

Goodman 等（2006）在中枢反向耦合假设的基础上，提出了一种前馈控制（feed-forward control）模型。该模型基于2 个假设：1）在中枢神经控制层面上存在2 个输入信号，即与任务变量相关的信号和与任务变量无关的信号。而基本变量（效应器层面的变量）的方差被认为是2 个变量的方差成分之和。2）神经控制器掌握着基本变量的微小变化与结果变量变化之间的映射信息（系统的雅可比矩阵），此模型中的感官反馈仅用于更新此映射信息，而不参与纠正正在进行的控制信号。该模型在实质上类似于Bullock 等（1993）所倡导的方法，Bullock 提出了一种神经元网络，该网络通过学习从末端效应器到关节坐标的坐标变换形成一种结构，这种结构可以从一组运动等效解中选择一个解。

3.2.3.2 结合中枢反向耦合机制和对照设置机制的前馈控制模型

Martin 等（2009）以手指在二维平面上的指向运动为例，建立了一个多自由度的运动生成模型，具体模型包括（图6a）：

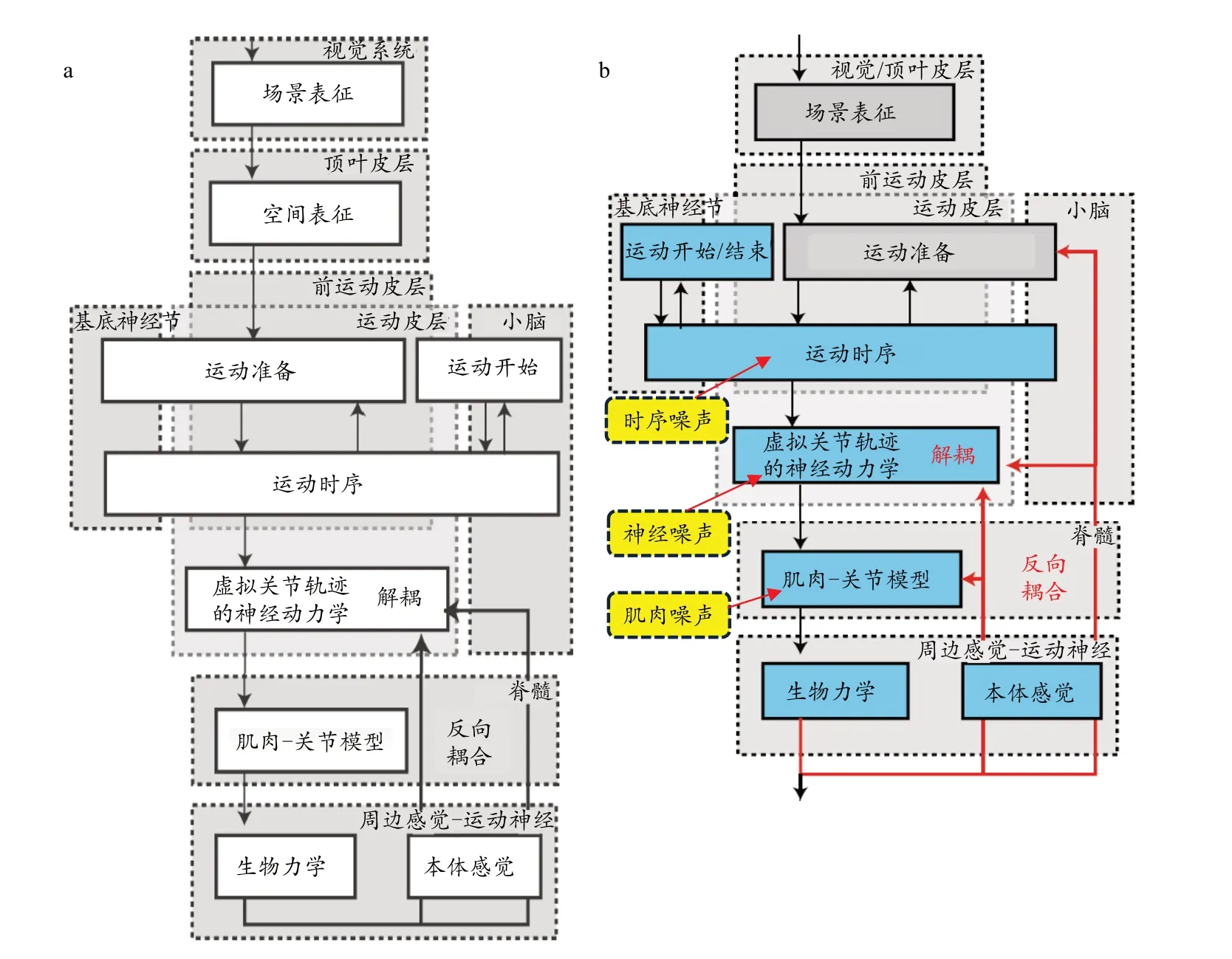
图6 多自由度的运动生成模型Figure 6. Motion Generation Model of Multi-degree Freedom

1）1 条回路（黑色实线）：本体感觉信息对虚拟关节轨迹的反向耦合回路。2）浅灰色虚线方框表示在中枢神经系统中信息处理过程的结构图。3）黑色虚线方框则表示不同的神经器官所控制的区域，包括视觉/顶叶皮层、前运动皮层、运动皮层、基底神经节、小脑、脊髓、周边感觉运动神经。4） 8 个模块（实线方框）：场景的神经表征（包括空间表征）和运动准备模块（灰色实线方框）已由其他研究者建模（Zibner et al.， 2011），因此在模型中仅用参数值表示。该模型重点对运动的起始和结束、运动时序、虚拟关节轨迹的神经动力学、肌肉-关节模型和生物力学5 个模块（蓝色实线方框）进行建模，而对于本体感觉模块则与虚拟关节轨迹的神经动力学相结合（形成反向耦合回路）进行建模。

该模型基于动态系统理论的思维，以神经元动力学为模型的核心。动态系统理论以过程为导向，符合生理学原理。神经元动力学包括：1）启动和终止运动的神经动力学；2）生成时序信号的神经振荡器，该信号可沿末端效应器的运动路径调节其节奏和进度；3）激活肌肉和关节运动的神经元动力学。该神经元动力学基于对照设置机制中的阈值控制，由人工神经网络通过接收来自神经振荡器的时序信号产生平衡点，平衡点的时间曲线会驱动每个关节的运动，从而生成虚拟的关节轨迹（Latash，2010a）。在此动力学模型中，移动末端效应器与不移动末端效应器的虚拟关节速度向量动态解耦。根据反向耦合机制，所感知到的实际关节设置被耦合回该神经元动力学模型中，更新虚拟轨迹，因此产生了未按原来神经指令执行的任务等效运动。任务等效运动、自运动、UCM 运动在本质上是相同的，均指在运动过程中基本变量所产生的变异不会影响任务结果。该研究的模型推演数据很好地拟合了实验测试数据，并发现关节速度包含大量不会移动末端效应器的自运动。Martin 等（2009）认为，低阻抗肌肉关节系统的控制不完善，以及多关节肌肉所引起的肌肉关节系统之间的耦合，是产生自运动的主要原因。

Martin 等（2009）进一步分析发现，这些自运动现象不是中枢神经系统预先计划好的，说明解决多自由度运动系统冗余的问题，并不是神经系统的首要任务。这与平衡点假说的理念一致，即神经控制层面实际上并没有解决冗余问题，只是限制了不同自由度之间可能的协调，而冗余问题的解决方案是在神经肌肉元素自身之间以及这些元素与环境之间的相互作用之后出现的（Feldman et al.，2009）。

Martin 等（2019）为检验噪声对运动变异的影响，以及解释UCM 协同的方差结构（VUCM-VORT＞0），在此前模型的基础上，增加了时序噪声、神经噪声、肌肉噪声等模型，这些噪声会对运动系统进行随机扰动（图6b）。另外增加了一条反馈控制回路，即本体感觉信息通过脊髓反馈至运动准备的回路（图6b 红色长实线），由于是快速的分立运动，反馈控制回路可以忽略。

该模型推演数据也很好地拟合了实测数据。通过改变模型中的不同组成部分，并记录其对方差结构的影响，发现产生UCM 协同的可能原因有：1）神经噪声和解耦的作用。运动指令层面上的神经噪声以及运动指令在与UCM 平行和与UCM 正交的2 个子空间上的解耦导致方差结构中出现UCM 特征。2）肌肉噪声和肢体不完美的控制。肌肉及其周边反馈控制不能完美地控制肢体，因此偏离了下行运动指令所规定的关节设置轨迹，从而表现为UCM 协同的方差结构。3）反向耦合的作用。反向耦合负责更新虚拟关节轨迹。运动过程中，一般会受到内部（神经噪声、肌肉噪声等）或外力的扰动而产生关节设置的变化，发送到肌肉的运动指令则根据实际感知到的关节设置进行更新，这与Martin 等（2009）的研究一致，即将感知到的关节设置反向耦合到运动指令中，运动指令随后在UCM 空间内顺从于感知到的关节设置。这种反向耦合可以被视为一种神经机制，其执行类似于Todorov等（2002）所提出的“最小干预原则”。反馈控制与反向耦合在本质上是相反的，在反馈控制中，运动指令会改变实际感知到的运动；而在反向耦合中，运动指令会顺从于实际感知到的运动（Martin et al.， 2019）。

3.3 探寻神经控制层面的UCM协同

尽管有行为学和神经病理学的证据支持UCM 协同，并且大量的假设模型也能有效地模拟UCM 协同，但这些证据仍然是间接的，因为在神经控制变量层面上解释机械层面上的观察结果并不容易。基本表现变量（如关节转动）不仅与神经控制变量有关，还与外力有关，包括依赖于其他关节运动的交互作用力（Latash， 2010a）。UCM协同也不是计划好的，而是由肌肉骨骼系统中相对较低的阻抗、互动力矩、多关节肌肉等控制问题所导致的（Martin et al.， 2009）。神经层面相比肌肉层面有更大的变异，肌肉层面相比肢体运动层面又有更大的变异，以致通过肢体运动层面的变异来分析神经的控制特征成为挑战（刘宇，2010）。因此，机械运动层面上的特定协变模式并不意味着神经控制变量之间必定存在协变。

根据对照设置假说，生物力学和肌电图等基本变量的变化是通过交互命令（reciprocal command，“R 命令”）和共激活命令（coactivation command，“C 命令”）进行间接参数控制的结果，这些命令定义了运动神经元池激活的空间范围（Madarshahian et al.， 2022）。R 命令与主动肌和拮抗肌中的运动神经元的交互控制输入有关，C 命令定义同时激活2 个相对肌群的空间范围（Latash et al.， 2021）。猴子的皮层记录以及关于人和动物的研究已经证明存在独立的神经元系统，以交互激活和共激活主动肌和拮抗肌（Feldman et al.，1995）。

随着UCM 分析方法应用的广泛和深入，一些研究者跨越运动学、动力学和肌电层面，尝试结合对照设置机制，将UCM 协同推广到神经控制层面的变量分析，即从基本力学变量或肌电变量推断R 命令和C 命令的变化，并探索在这些控制变量空间中维持控制命令输出稳定所表现出的协同（Ambike et al.，2016；Reschechtko et al.，2017）。这些研究采用多指用力任务，发现在｛R 命令；C命令｝空间中有很强的稳定总命令输出的UCM 协同，但将这种方法扩展到其他任务有较大难度，也无法量化预期协同调整，因此尚未推广至实践应用（Latash et al.，2021）。将该方法应用于分析单个运动单位空间内（Madarshahian et al.，2021）和多个运动单位空间之间（Madarshahian et al.，2022）的协同也取得了一些进展，但这些研究尚处于初步尝试阶段。

3.4 小结

综上所述，神经系统在运动控制的过程产生UCM 协同的基本步骤为：

1）中枢神经系统根据特定任务目标预设虚拟的末端效应器轨迹，指定对照设置，以确定各肌肉和关节的激活阈值。

2）在实际执行动作的过程中，由于运动控制系统的不完美和复杂性，在系统内部会产生时序噪声、神经噪声、肌肉噪声等，再加上有外力扰动的情形下，会导致运动偏离原先的设定（运动变异），此时肌肉已不能完全按神经系统原先发出的指令执行。环节之间的相互补偿使运动仍然不会偏离任务目标。该过程实质上相当于中枢反向耦合的过程，即运动指令在UCM 空间内顺从于感知到的关节设置，从而产生VUCM。这个过程仅在脊髓中就可以完成。如果通过环节之间的相互补偿仍不足以抵抗系统噪声或（和）外力的扰动，且动作持续时间很短，来不及进行反馈调节，则会使运动偏离任务目标，此时会产生VORT。如果动作的持续时间足以让中枢神经系统进行反馈调节，则发生：

3）反馈调节机制。进行反馈调节的主要中枢是小脑。需注意的是，UCM 协同产生的过程有几个特点：其一，据反馈控制机制，运动层面的UCM 协同是中枢神经系统在关节之间主动协调的结果；但据前馈控制机制，运动层面的UCM 协同不一定非得中枢神经系统主动控制，因为运动指令在UCM 空间内会顺从于感知到的关节设置。其二，产生UCM 协同的主要来源有神经和肌肉系统产生的噪声、各运动环节之间的互动力矩、多关节肌肉的控制，其中各运动环节之间产生的互动力矩可能是最主要的来源。其三，对于一个多自由度的运动，不一定会产生反馈调节的控制，但由于环节间互动的动力学起作用，一定会产生反向耦合的控制。其四，随着某专项技能的提高，利用环节间互动力矩的能力和多关节肌肉耦合不同关节的能力会提高，相应的产生UCM 协同的能力也会提高。

4 UCM协同在动作行为领域中的应用

UCM 理念自创立以来，已得到广泛的应用。其中包括技能学习过程中运动协同的变化、神经性疾病患者的动作控制、健康老龄化、儿童动作发展、运动（职业）技能控制等方面的研究。

4.1 技能学习过程中运动协同的变化

相关领域对运动技能的学习进行了大量研究，从不同的角度提出了运动技能形成的阶段理论。巴甫洛夫根据经典条件反射理论，强调以大脑皮质活动为基础的暂时性神经联系，将运动技能的形成分为泛化、分化、巩固和自动化3 个阶段（王瑞元 等，2013）。有学者根据执行动作过程中注意分配的变化，将技能形成分为认知、固定、自主3 个阶段（Anderson， 1982； Fitts et al.， 1967），或者分为控制处理和自动化处理2 个阶段（Schneider et al.， 1977）。而Schmidt（1975）根据一般动作程序理论，认为练习的过程就是建立和提取一般动作程序，并对力量、速度、方向等动作参量形成动作图式的过程。以上理论主要是从大脑皮层的某些变化，或者大脑皮层对信息的处理方式等特征出发，对运动技能的形成进行分类，但尚未涉及运动协同方面的特征。

早在20 世纪40 年代，苏联生理学家Bernstein（Latash et al.，1996）就以自由度数量变化的理念提出技能获得的三阶段理论：第一阶段，通过对动作的限制，以消除冗余的自由度；第二阶段，一些自由度逐渐被释放，导致在基本变量层面上的变异增加；第三阶段，各自由度之间变得更加协调，以利用动作执行过程中产生的反应式现象，如关节之间的互动力矩。因此，从运动生物力学的角度分析认为，利用环节间反作用力的能力提高，改善了协调能力（Bernstein，1967）。运动技能提高的过程实际上就是神经控制的主动肌肉力矩对外力矩和被动的反作用力矩的控制、协调与适应的过程（刘宇，2010）。技能学习的早期阶段，限制部分自由度的运动似乎能使控制更简单。然而，有研究发现，在快速运动期间，保持众多关节中的其中一个关节不动，需要精确修改穿过关节的肌肉控制信号（Koshland et al.，1991； Latash et al.，1995）。也就是说，虽然关节未动，但对关节的神经控制并未减弱。

从肌肉协同理论的角度看，通过训练会产生更加优化的运动协同。国内学者对该理论和现象进行综述或应用研究指出，协同作用激活系数和肌肉协同向量都能被技能学习调节（杨毅 等，2020），随着动作技能水平的提高，修饰后的肌肉协同元会在更加困难的相似动作任务中被共享（张百发 等，2021）。但肌肉协同理论所表征的是一些主要基本变量的共享模式，因此只能发现练习对共享模式特征的影响。而运动协同的另一个特征，即基本变量（自由度）之间协变的灵活性和结果变量的稳定性，则需借助UCM 协同理论进行分析（Latash et al.，2007）。由于动作的起始条件和外力都在不断变化，以及环节之间会产生互动力矩，基本变量之间的协同模式不是一成不变的，而是能够相互补偿因误差产生的变异，从而保持动作结果的稳定（Wu et al.，2014）。

从UCM 协同理论的角度看，技能学习的过程主要涉及的是各自由度协变模式的变化，而不是自由度数量的变化（Wu et al.， 2014， Yang et al.， 2005）。如果练习能使基本变量空间中的变异增加，同时使结果变量的变异减少，则是增强了基本变量之间的协变（Wu et al.，2014）。而协变模式的量化则可以ΔV作为评判指标。如图7 所示，E1和E2分别表示2 个基本变量，虚直线表示线性化的UCM 空间，椭圆形区域表示实际的基本变量值变异的范围。沿VUCM方向的变异不会影响任务变量值，被认为是动作技能提高、动作灵活性增强的表现，沿VORT方向的变异则会使任务变量值改变，被认为是动作技能较差、动作不稳定的表现。图7 展示了通过练习所可能产生的5 种ΔV的变化：图7A 表示2 种变异成比例改变，ΔV不变；图7B 表示VUCM比VORT减少得更多，ΔV减少；图7C、D、E 则分别表示VUCM减少、不变或增加而引起的ΔV增大。有关准确性动作的研究显示，练习可能使ΔV降低（Domkin et al.，2002）、不变（Domkin et al.，2005）或增加（Kang et al.，2004； Yang et al.， 2005），尚未形成一致结论。练习引起动作ΔV改变而导致动作协调模式的变化不但发生在健康年轻人群，还发生在唐氏综合征患者（Scholz et al.，2003）和健康老年人群（Olafsdottir et al.，2008； Wu et al.，2013）中。但相关研究中鲜见图7E 所示的变异情况。

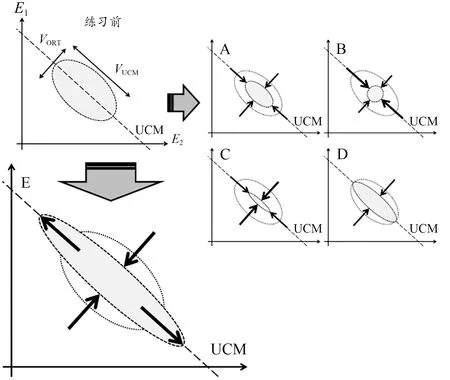
图7 练习后基本变量（E1、E2）在空间中5种可能的方差结构变化Figure 7. Five Possible Changes in the Structure of Variance in the Space of Two Elemental Variables （E1， E2） after Practice

Latash（2010b）结合UCM 理念和平衡点假说提出了技能学习的两阶段模型：第一阶段，VORT显著减少，同时VUCM变化不明显；第二阶段，VUCM减少，同时VORT变化不明显。第一阶段的变化可解释为根据任务的要求增强了动作协同。在平衡点假说中，第一阶段可被视为由2 个步骤组成：1）根据任务目标设置适当的对照设置轨迹；2）为稳定对照设置轨迹，多关节（多肌肉）的协同更加完善（Latash，2010b）。在第二阶段，运动的控制所涉及的因素除了准确和稳定地完成所要求的任务之外，还包括对动作美学、速度、舒适性、经济性以及抵抗外部扰动等因素的考虑，这导致在UCM 内对各单个基本变量组合的选择更具特异性，从而引起VUCM减少（Latash，2010b； Wu et al.，2014）。功能磁共振成像研究发现，长期的训练能使运动员在执行动作时的脑区激活更加精简高效，发展出有针对性的、高效的，并只与任务相关的神经网络组织（娄虎 等，2020；Milton et al.，2007）。一项壶铃摆动实验研究发现，在最初的练习之后，VUCM仍然很高，这表明被试在持续探索可能的运动解决方案；在多次练习之后VUCM降低，可能是被试对原有解决方案进行选择性的利用，即产生了动作定型（Beerse et al.，2020）。

综上，练习不是寻求产生最佳绩效的唯一动作模式，而是各基本变量之间协调关系的发展。在练习前期增强了中枢对VORT的控制，以保证任务完成的准确性，而不受中枢控制的VUCM基本保持恒定，体现了对可能的运动解决方案的探索。在练习后期，VUCM的降低则体现了任务特异性要求。

4.2 神经性疾病的诊断和康复

4.2.1 中风后遗症

中风后运动的特征通常表现为：不对称的步态模式、躯干和非麻痹肢体的代偿性运动、运动协调模式改变和动作变异增加（Lofrumento et al.， 2021）。有关中风患者与健康人群任务变异表现的研究得出了中风患者ΔV降低（Reisman et al.， 2005）、ΔV无显著变化（Jo et al.，2016b；Reisman et al.， 2003； Srivastava et al.，2016）、VUCM相似（Gera et al.，2016；Reisman et al.， 2003；Srivastava et al.，2016）、VUCM大于对照组（Kang et al.，2017）、VORT大于对照组（Gera et al.，2016； Kang et al.，2017；Reisman et al.，2005）等不同结论；以及中风患者在做伸手触够动作时，稳定重心的ΔV无差异，但在稳定终点位置时ΔV偏低（Tomita et al.，2020）。

值得注意的是，Reisman 等（2003，2005）的2 个研究得出了不同的结果，这2 个研究的测试对象均为中风患者，其任务均为做伸手触够动作。不同的是，做伸手触够动作时，在2003 年的实验中，其触够幅度不超出手臂的范围，而在2005 年的实验中，触够幅度超出了手臂的范围，必须靠躯干的转动使上臂产生外展，才能完成任务。而对中风患者来说，由于皮层的受损，导致上臂的外展和肘关节的屈曲存在病态的耦合，使肘伸展能力不足，减少了肘关节的有效活动范围，从而限制了环节之间的协同能力（Reisman et al.， 2005）。

总的来说，在有关UCM 的ΔV比较上，大部分研究并没有发现中风患者与健康人群存在显著差异。这表明中风患者保留了结合基本变量以稳定任务绩效的协同能力。但这并不意味着中风患者协同的共享模式没有发生变化。Reisman 等（2003）指出，与对照组相比，虽然VUCM和VORT无显著性差异，但中风患者的运动时间更长，手的路径变化更大，绝对指向误差更大。有证据表明，由于下行神经通路的部分中断，中风患者的大肌群肌肉独立性和共收缩性降低（Clark et al.，2010）。

4.2.2 帕金森

姿势不稳或运动稳定性受损是帕金森病的主要致残特征（Ambike，2021；Freitas et al.，2020）。研究发现，与健康对照组相比，帕金森患者的ΔV更低（Falaki et al.，2016，2018），预期协同调整幅度更低（Jo et al.，2015），并同时表现出延迟（Falaki et al.，2018； Park et al.，2012）。在知觉上，动觉知觉表现出不同形式的受损（Ricotta et al.，2021）。

帕金森患者在早期并不会表现出姿势不稳定症状（Falaki et al.，2016）或者明显的脑部病变症状（Park et al.，2012），但在UCM 协同特征上却表现出显著的恶化（ΔV降低、预期协同调整延迟等）。例如，Falaki 等（2016）发现帕金森病患者的ΔV降低，但站立时压力中心向前或向后移动的幅度和峰值速率未见显著差异。因此，UCM 测量可以作为可靠的早期预测指标，以检测帕金森患者在动作稳定性上的神经控制问题。鉴于通常只有在脑部黑质严重变性后才能做出诊断（Park et al.，2013a），应充分发挥UCM 测量的早期诊断作用，以便更早介入治疗（Vaz et al.，2019）。

帕金森病患者服用左旋多巴胺能药物后，通过增加VUCM（Falaki et al.，2017）或减少VORT（Park et al.，2014），进而增加ΔV。当脑深部刺激处于开启的状态时，患者ΔV未发生显著变化，但预期协同调整有显著改善，调整幅度更大且发生得更早（Falaki et al.，2018）。

4.2.3 其他神经性疾病

多发性硬化症（Jo et al.，2016a）、橄榄体脑桥-小脑萎缩（Park et al.，2013b）、脊髓小脑变性（Asaka et al.，2011）等患者的ΔV都存在不同程度的降低。痉挛性脑瘫患者在多手指用力任务中，协同用力以稳定总力量的能力与正常人群无显著差异，但预期协同调整的能力更弱（Kong et al.，2019），在步行时的单肢和双肢支撑阶段，控制重心和头部位置稳定性的能力弱于健康对照组（Song et al.，2021）。此外，青春期前的唐氏综合征儿童行走时控制身体重心的ΔV显著低于正常的同龄儿童（Black et al.，2008）。

4.3 健康老龄化

进入老年期后，人类神经运动系统会发生各种生理变化，特别是中枢神经系统结构中的神经元会发生萎缩或死亡（Gorniak et al.， 2011）。老年人会表现出中枢和外周神经系统的亚临床功能障碍，如皮质间抑制受损（Beijersbergen et al.， 2013），出现更大、更慢的运动单位（Cole et al.，1999），肌肉共激活增加、肌束神经再生、肌纤维萎缩、肌纤维减少（Thompson，2009），以致肌力降低。UCM 协同中的稳定性指标（ΔV）和敏捷性指标（预期协同调整）对轻微的运动障碍均十分敏感。健康老龄化会导致ΔV和预期协同调整指数下降（Olafsdottir et al.， 2008）。中枢神经系统中感觉和运动神经元的变化可能是老年人运动协同能力降低的潜在机制（Latash et al.， 2006； Olafsdottir et al.，2007）。

Shafizadeh 等（2019）对12 篇有关多指用力的实验研究进行了元分析，发现衰老对多指任务协同的影响非常显著。老年人在这些任务中所表现出的UCM 协同能力显著低于年轻成人，无法正常维持手指握力的稳定性。除了多指协同的任务外，老年人在姿势控制（Freitas et al.，2012）、步行（Wang et al.， 2017）以及“坐-站立”（Anan et al.，2017）等过程中稳定重心的多关节协同能力也比年轻人低。过度的肌肉（主动肌和拮抗剂）共收缩可能是老年人重心稳定控制能力下降的主要原因（Wang et al.，2017）。过度的肌肉共激活会影响姿势稳定性，容易失去平衡而增加跌倒的风险（Yamagata et al.， 2019a）。

然而，一些研究发现，老年人能保持与年轻人相同水平的协同能力。这类研究主要涉及稳定指向或稳定触够目标的上肢多关节协同（Greve et al.，2017；Xu et al.，2013），以及步行时稳定摆动脚横向位置（Krishnan et al.，2013），或双脚支撑阶段的合力（矩）（Cui et al.，2020）、“坐-站立”时稳定矢状面内重心（Greve et al.， 2019）的环节（或关节）协同能力。

Xu 等（2013）认为，上肢多关节指向或触够任务相对于精确的手指力量产生任务，是日常生活中更常用的动作，许多日常动作需要整合多个来源的感觉信息，在这些自然的动作任务中并未发现老年人的协同能力受损。

更有趣的是，有研究发现，老年人表现出高于年轻人的协同水平。这类研究主要涉及稳定触够方向（Krüger et al.，2013）、“坐-站立”时稳定地面反作用力（Greve et al.，2013）、步行时稳定摆动脚的横向位置（Eckardt et al.，2018），以及稳定步长（Rosenblatt et al.，2020）的关节协同能力。此类研究认为，老龄化会导致稳定某些任务变量的协同能力下降，也会引起稳定其他任务变量的协同能力增强（Krüger et al.，2013）。释放某些自由度以稳定重要任务变量，是神经肌肉系统补偿衰老所致的力量不足的策略（Greve et al.，2013）。年龄会影响执行动作的准确性，但不一定会影响执行动作的灵活性（Greve et al.，2017）。变异的增加（VUCM的增加＞VORT增加）并不是运动控制能力下降的标志，而是神经肌肉系统的一种有意识的策略，以补偿可能与年龄有关的力量和平衡能力下降的情况（Eckardt et al.，2018）。但只有在最大限度地发挥神经肌肉功能时，才可能动用更多的运动协同，以补偿与年龄相关的神经肌肉功能缺陷（Greve et al.，2019）。例如，Greve等（2013）研究发现，在执行“坐-站立”任务期间，当力量需求接近极限时，老年人稳定地面反作用力的ΔV增加，因此，实验条件的控制是影响老年人协同能力发挥的重要因素。

有关老年人步行的系列研究发现，有高跌倒风险的老年人相比低跌倒风险的老年人，稳定摆动脚（额状面内）的ΔV显著更高（Yamagata et al.，2019b，2019c），相反，稳定身体重心（垂直方向）的ΔV显著更低（Yamagata et al.，2021）。提示，所选择的受控变量（任务变量）不同，所得出的ΔV差异可能较大。从UCM 协同的分析过程可以看出，并不是所有变量都可作为中枢神经系统控制的变量，如果将实际不受神经系统控制的变量作为受控变量，则研究结果反映不出实际的协同能力，甚至可能产生误导。从步行的稳定性看，身体重心的稳定显然比摆动脚的稳定更重要，因此，身体重心的稳定可能是神经系统优先控制的变量。如前所述，老年人稳定重心的多关节协同能力显著低于年轻人。因此，通过对身体各环节的协同控制以稳定身体重心，可作为老年人抵抗跌倒风险的重要能力。Wang 等（2019）的研究发现，在受到扰动后稳定身体重心的过程中，有丰富舞蹈经验的老年人表现出更高的多肌肉ΔV和更早的预期协同调整，进一步验证了身体重心控制的重要性。

综上所述，大部分研究表明老年人在多指用力任务中稳定总力，以及在各种任务中稳定身体重心的协同能力显著低于年轻人。老年人步行时稳定身体重心的ΔV越低，跌倒的风险也更大。也有研究发现在执行其他任务时，老年人的协同能力与年轻人无显著差异，甚至更高，其原因可能有：1）不同任务的神经控制机制可能不同（Shafizadeh et al.， 2019）；2）协同能力的提高是神经肌肉系统补偿力量和平衡能力下降的一种有意识的策略（Eckardt et al.，2018），当力量需求接近极限时，老年人会动用更多的运动协同（Greve et al.，2013，2019）；3）所选择的受控变量可能并不是神经系统实际要控制的变量，导致研究结果反映不出实际的协同能力。因此，后续研究可根据不同的任务，选择合适的受控变量（任务变量）和实验条件，以进一步探索健康老龄化是否，以及如何影响多关节协同和多指用力控制。

4.4 儿童动作发展

儿童首先要学会调节身体各环节的运动以控制身体重心，然后才能达到类似成人的运动协同能力，这一过程需要约10 年的时间（Wu et al.，2009）。Shaklai 等（2017）通过多指按压任务发现，4～12 儿童的手指用力ΔV随着年龄增长呈线性增加，说明手指间发力的协同能力岁年龄增长提高，并且这种提高不是通过增加VUCM，而是通过选择性地减少VORT实现的。Golenia 等（2018）研究了儿童期中期（5～10 岁）的指向触及动作的发展，发现随着年龄的增长，目标等效变异（即VUCM）和非目标等效变异（即VORT）逐渐下降，且目标等效变异的下降幅度大于非目标等效变异的下降幅度，这表明随着年龄的增长，运动ΔV下降，这样的结果似乎不符常理。Golenia 等（2018）认为可能与儿童的探索行为有关。在儿童中期，协同作用是在这些探索过程的基础上得到完善的，这一方面反映在目标误差逐渐减少，另一方面反映在目标等效变异和非目标等效变异的减少。大多数年幼儿童的探索发生在协同作用内部（目标等效变异），这种探索随着年龄的增长迅速减少。然而，寻找属于协同的一系列解决方案需要在协同的边界进行探索。可能年龄较大的儿童更接近协同作用的边界，这意味着有更多的机会在协同作用外部（非目标等效变异）进行搜索，这可能解释了为什么非目标等效变异在发育过程中比目标等效变异的变化速度更慢。有研究表明，如果目的本身是促进变化，控制稳定性的丧失可能是有益的（Latash， 2021）。

4.5 运动（职业）技能控制

应用UCM 方法对专业运动技能或职业技能的运动协同特征进行分析，有利于揭示技能水平高低的本质区别。目前的研究主要集中在目标任务控制和身体重心控制的过程中所产生的UCM 协同方面。

4.5.1 目标任务的控制

Morrison 等（2016）对高尔夫挥杆击球动作分析发现，高水平球手比低水平球手能更好地利用自身富余的（abundant）自由度，据此认为，要想在高尔夫运动中达到更高的技术水平，可能不仅仅在于技术的最佳化，而更多地在于发展对人体中富余自由度的控制。

Ⅰino 等（2017）研究发现，在乒乓球正手击上旋球的动作中，在击球时影响拍面角度（垂直方向）的关节角度的变异程度上，高水平球员显著小于中水平球员，并且在击球时稳定拍面角度（垂直方向）的冗余利用程度上，高水平球员趋于更大，由此得出，在乒乓球的击球瞬间，利用关节设置（joint configuration）的冗余来稳定拍面角度的能力可能是影响动作结果的一个关键因素。

Serrien 等（2018）对6 名高水平反弓射箭运动员在瞄准时的姿态控制和上肢动作的研究发现，在准确性高的射箭中（得9、10 分），稳定箭头方向的目标等效变异显著大于非目标等效变异。相反，准确性较低的射箭中（得6～8 分），在瞄准阶段的大部分时间内未能达到显著差异。该分析表明，精英射手没有必要（甚至也没有可能）在瞄准过程中最小化所有自由度的运动，而是利用冗余运动链的变异结构，从而稳定相关表现变量（箭头方向）。

4.5.2 身体重心的控制

Mӧhler 等（2019）以13 名有经验的年轻跑步者为测试对象，研究运动疲劳对跑步时重心轨迹控制的影响发现，受试者处于疲劳状态时，在跑步腾空阶段的VORT（任务相关变量）增加，但ΔV并没有发生显著性变化。表明有经验的跑步者在疲劳状态下也能够有效地控制身体重心的轨迹。Mӧhler 等（2020）的另一项研究比较了不同水平的跑步者（新手和专家），在不同速度（10、15 m/s）跑步时控制重心的差异。研究发现：1）不同速度下，不同水平的跑步者在稳定重心的ΔV上并无显著差异，且均为ΔV＞0，表明2 组人群在跑步中都有稳定身体重心轨迹的协同作用。2）2 种类型的变异（VUCM和VORT），在支撑阶段显著大于腾空阶段。3）在速度为15 m/s 的情况下，新手组2 种类型的变异（VUCM和VORT）均显著大于专家组；在速度为10 m/s 的情况下，2 种类型的变异无组别差异。表明专家组在不同的速度下，采用了更一致的跑步方式。

Koh 等（2020）比较了有职业舞蹈经验的人群和普通人群在面对突然的外界扰动时，控制身体重心的能力。研究发现，与普通人群相比，有舞蹈经验者在控制身体重心时，显示出更大的VUCM，表明舞蹈者能更充分地利用身体的冗余自由度。由此可推断，长期的专门舞蹈训练提高了中枢神经系统利用身体冗余自由度的能力。需要特别指出的是，该研究采用单个环节质心的相对坐标作为基本变量（之前的研究一般是采用关节角度作为基本变量）。另外，计算雅可比矩阵的对照设置并不是有扰动时多次重复动作的平均值，而是无扰动时的平均值。

林辉杰（2013）结合肌肉协同理论和UCM 分析了掷铁饼动作的协调特征，发现在精英组和普通组运动员在运动协调元的灵活性表现出明显的差异。精英组中，在控制铁饼速度、人体重心位移、左脚位移、肩髋角以及拉引角等任务参数时，运动协调元活动的功能变异性（VUCM）更高，表明对这些运动任务参数的控制程度更高。

5 总结与展望

UCM 协同是一种为稳定目标任务，各基本变量之间进行误差补偿的协同。一些动物实验和神经病理学现象表明，控制UCM 协同的神经部位存在于皮质下，包括脊髓、小脑和基底神经节。许多研究也发现在运动学、动力学和肌电层面都存在UCM 协同现象，表明几乎在所有的运动冗余系统中都会产生UCM 协同。一些神经控制模型也有效地解释了UCM 协同产生的机制和过程，发现神经系统和肌肉系统产生的噪声，以及各环节之间的互动力矩和多关节肌肉对不同关节的耦合，可能是产生UCM协同最主要的原因。但以上的研究证据仍然是间接的，难以证伪。

为了进一步验证UCM 协同理论，获得更直接的证据，未来的研究可探索无损的，且能直接干预脑深部神经区域的方法。目前能够对这些区域进行刺激干预的手段有脑深部刺激和光遗传学等技术，但脑深部刺激技术需要在患者脑内特定的神经核团和神经组织中植进电极，只能应用于重症病人的治疗；光遗传学技术目前还处于动物实验阶段，距临床应用还有许多问题亟待解决。因此，在这些技术能无损地应用于普通人群的实验之前，病理学案例和动物实验仍然是UCM 协同在神经控制层面上的主要证据。另一个路径是应用环节互动的动力学方法。例如，针对执行多自由度的运动，对环节之间互动力矩的利用率和多关节肌肉对各关节的耦合程度进行量化，并将这些指标与UCM 协同指标进行相关性分析，以验证UCM 协同产生的主要来源是否来自于各环节之间的互动力矩和多关节肌肉的耦合。

目前将UCM 协同应用于体育领域的研究尚不多。原因可能是在体育运动中，特别是竞技体育运动中，动作和环境要复杂很多，这会大大增加实验测试时的控制难度。但竞技性运动因为对动作质量要求高，更注重神经系统对动作的控制，因此理论上更容易找到高水平运动员在运动神经控制方面的证据。期待未来有更多的研究基于UCM 协同理念，设计接近运动实际情形且可控的实验方案，以探索高水平运动员的运动控制机制。针对特定的运动技能，结合UCM 协同以及其他协同理论的原理，设计有效提高协同控制能力的方法和手段，也是值得今后深入探索的课题。