基于结构平衡理论和高阶互信息的符号网络表示学习算法

郁 湧，钱天宇，高 悦，艾合买提尼牙孜，刘金卓*

(1.云南大学软件学院 昆明 650504；2.云南大学云南省软件工程重点实验室 昆明 650504；3.云南大学跨境网络空间安全教育部工程研究中心 昆明 650504)

在一些网络中，节点之间的连接关系根据不同的涵义可以分成两类：正关系和负关系。其中，正关系表示积极的涵义，如喜欢、信任、合作、支持等；而负关系表示消极的涵义，如讨厌、不信任、对立、否决等[1]。若将相关网络中的正关系标注为正号，负关系标注负号，就形成了一个符号网络。目前，符号网络存在于很多的领域，如社交网络用户之间存在朋友与敌人关系、生物领域细胞间存在促进与抑制作用、国际关系中国家之间存在合作与敌对关系、游戏网络中玩家存在协作与竞争关系等。对符号网络进行分析和研究也越来越成为社会网络研究中不可忽视的部分[2]。

在针对符号网络结构的研究中，一个重要的问题就是如何合理有效地对符号网络的结构信息进行表示。传统的网络结构表示主要采用高维稀疏矩阵的形式，但高维稀疏矩阵往往需要更多的时间和空间成本。随着人工智能和机器学习的突飞猛进，越来越多的研究领域都融入了深度学习等相关技术，而传统的网络结构表示方法都无法直接应用这些算法，为此，研究人员开始转向探索网络节点的低维向量表示的方法，即网络表示学习(network representation learning)或网络嵌入(network embedding)。网络表示学习是衔接网络中原始数据和网络应用任务的桥梁，旨在将网络中的节点表示为低维稠密向量，并且能够最大程度地保留原网络中的结构信息和特性。

虽然，网络表示学习的研究已经取得了一系列的成果，但现有的方法大都仅适用于无符号网络，将其应用于符号网络会导致网络中符号涵义等关键信息丢失，难以获得质量较高的节点表示学习。如在朋友敌人网络中，互为敌人关系的节点可能会在嵌入空间被放得很近，这十分不合理。为此，需要研究针对符号网络的表示学习方法。

本文基于结构平衡理论和高阶互信息原理来对符号网络的拓扑结构进行研究，旨在建立结合机器学习与传统网络理论的相似度指标，提出一种新的符号网络表示学习方法SNSH (signed network representation learning algorithm based on structural balance theory and high-order mutual information)，并用于解决无向符号网络中的链路符号预测问题。

1 相关工作

网络表示学习旨在用低维、稠密、实值的向量表示网络中的节点。一般来说，通过网络表示学习得到的节点嵌入需要体现节点的各项特征，并能在各种下游任务取得良好的性能。

网络表示学习已被广泛应用于节点分类[3-4]、链路预测[5]、聚类[6-8]、可视化[9]、节点排序[10-11]、社区分析[12]、图形生成[13]、异常检测[14]等任务，并取得了良好的效果。节点分类的目的是根据其他节点和网络的拓扑结构来确定节点的标签；链接预测是指预测未来可能出现的缺失或链接；聚类用于寻找相似节点并将它们分组；可视化可用于洞察网络结构[15]。在符号网络中，主要的下游任务是链路符号预测[16]，即预测节点之间边的符号类型。

网络表示学习的方法大致可以分为矩阵分解、随机游走、深度学习和其他4 个类别。如基于矩阵分解的Laplacian Eigenmaps[17]、HOPE[18]等，基于随机游走的DeepWalk[19]、node2vec[20]等，基于深度学习的SDNE[21]、DNGR[22]、GCN[23]等，还有混杂的LINE[24]等。

对于符号网络表示学习，SiNE[25]通过多层神经网络来优化基于结构平衡理论指导的目标函数，对符号网络的表示进行了学习。Signet[26]修改了word2vec[27]模型的采样方式，通过随机游走构造高阶结构平衡环来拟合远距离邻居节点对节点符号的影响。SGCN[28]将GCN 推广到符号网络中，并基于平衡理论设计了一种新的信息聚合器。SNEA[29]利用自注意机制来提高符号网络表示学习的效果。SDGNN[30]引入了一种新的逐层有向符号网络GNN模型。但这些方法都并未考虑高阶互信息对节点嵌入的影响。

本文提出的基于高阶互信息的符号网络表示学习算法，通过将符号网络中的关系反转，生成网络的负符号嵌入、负特征属性向量、负局部概括等负信息。该项工作通过负信息强化网络的正信息，以此捕获网络中高阶互信息所隐含的信息量。

2 问题定义

本文涉及的符号网络的定义如下：将符号网络用无向图表示，记为G=(V,E,S)。其中V代表社交网络中节点的集合，E代表网络中节点之间关系的边集合，S={1,-1}代表边的符号关系。对于∀e(i,j)∈E， 则s(i,j)表 示节点vi与 节点vj之间的关系符号，s(i,j)=1代表“+”，表示节点之间具有信任、合作、友好、支持等积极关系；s(i,j)=-1代表“-”，表示节点之间具有不信任、敌对、讨厌、否决等消极关系。

2.1 结构平衡理论

结构平衡理论是无向符号网络研究的理论基础，为无向符号网络的结构分析提供了依据。根据该理论，在无向符号网络中，由k(k≥3)条边组成的闭合环是结构平衡的当且仅当该环上所有边的符号之积为正。文献[31]研究表明，真实符号网络中结构平衡环的数量远大于不平衡环的数量，且随着网络结构的演变，不平衡的结构会朝着平衡的结构转换。此外，文献[32]用大量实证分析表明，结构平衡理论能更好地捕获并分析无向符号网络中节点间的相互作用模式以及结构平衡性。

结构平衡理论[33]最初仅在个体层面上提出，接着由文献[34]在群体层面的图论形成中加以推广，而后又由文献[35]发展为可聚类图的概念。最近，结构平衡理论被扩展为符号网络中的一种结构，它应确保节点的“朋友”比“敌人”更近[36]，即节点的位置应该离“朋友”(或具有正链接的节点)比“敌人”(或具有负链接的节点)更近。这种节点之间的结构描述如图1 所示。图中，对节点1 来说，它的“朋友”节点2 在特征空间上的距离应当相对于它的“敌人”节点3 来说会更近些。

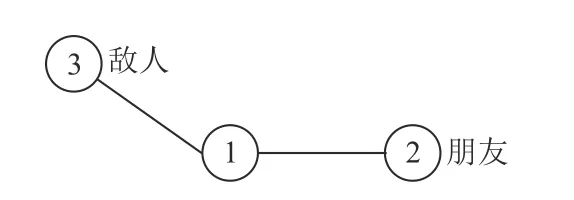
图1 结构平衡理论示意图

2.2 互信息

互信息可以度量两个随机变量之间的相互依赖性。给定两个随机变量X和Y，它们的互信息为：

式中，H(X)和H(X|Y)分 别表示熵和条件熵；H(X,Y)表示X和Y的联合分布。

为了测量多个随机变量之间的相互依赖性，在信息论中引入高阶/多元互信息的概念[37]。高阶互信息是互信息在随机变量数目增多时的推广，给定N个随机变量，高阶互信息的定义与互信息的定义类似，具体为：

高阶互信息不仅能捕捉所有随机变量对之间的互信息，还能衡量随机变量间的协同作用。

2.3 深度图互信息

深度图互信息( deep graph infomax, DGI )[38]是一种自监督或无监督的机器学习方法，其主要思想是最大化网络G:I(h,s)的概括向量s和节点嵌入hi之间的互信息。

DGI 使用负采样来最大化I(h,s)，首先它通过函数G=生 成一个补图， 然后使用同一个编码器来分别获得正图的节点嵌入和补图的节点嵌入，本文考虑到符号网络的特殊性，通过转换链接的符号正负来生成负网络。即对于负网络，=-si j，其余属性与图G保持一致。

正网络G通过聚合网络中所有节点的方式得到整图的特征表示，即概括向量，对于给定的概括向量s，DGI 使用一个鉴别器D来区分正网络嵌入hi和 负网络嵌入。

给定节点嵌入hi、概括向量s和负节点嵌入，可以通过下面的目标函数来最大化hi和s之间的互信息：

式中，D是一个用来区分负节点嵌入和真实节点嵌入的鉴别器； Θ表示参数空间； E表示期望。

3 SNSH 算法

3.1 算法的基本框架

本文提出的基于结构平衡理论和高阶互信息的符号网络表示学习算法SNSH，通过改进的上下文词向量模型得到节点的局部符号嵌入，又通过一个单层的图卷积神经网络(graph convolutional network,GCN)得到网络的局部嵌入矩阵和全局概括向量，同时使用节点的出/入度等有价值特征作为其特征属性向量。本文通过最大化这三者间的高阶互信息，挖掘符号网络中隐含的内部信息、外部信息与联合信息。

本算法由局部符号信息拟合、网络结构拟合、特征属性向量构造和最大化高阶互信息4 个部分组成，其基本框架如图2 所示。

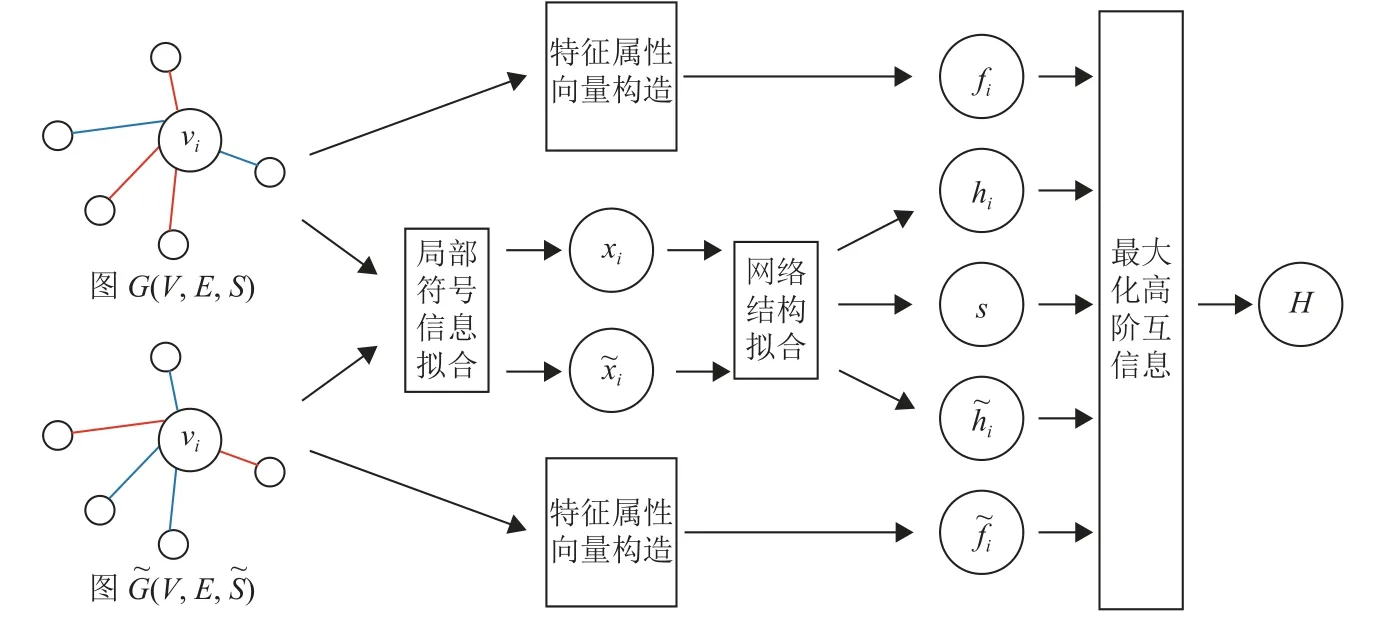
图2 算法整体框架图

1) 局部符号信息拟合

局部符号信息拟合用于得到符号网络中节点的局部符号信息。该模块改进了传统上下文的节点嵌入模式，首先根据节点的直接邻居构造正负关系邻居集，接着基于结构平衡理论，使用新的负采样方式优化节点嵌入，从而捕捉节点对与直接邻居间的符号信息。

2) 网络结构拟合

网络结构拟合用于进行全局网络结构传播拟合。该模块使用能体现网络符号信息特征的嵌入作为输入，经过单层GCN 的聚合，得到体现网络局部特征的嵌入矩阵H与体现网络全局特征的概括向量s。

3) 特征属性向量构造

特征属性向量构造用于得到综合考虑节点内在特征的特征属性向量。在该模块中对每个节点计算其度数、正邻居节点数、负邻居节点数以及体现节点建立正向链接趋势的指标，并将其构成节点特征属性向量。这些指标在传统符号链路预测方式中被证明能够有效体现节点特征。

4) 最大化高阶互信息

最大化高阶互信息用于最大化符号网络节点的高阶互信息，涵盖节点嵌入与概括向量之间的外部信息量、节点嵌入与特征属性向量之间的内部信息量，以及节点嵌入与概括向量和特征属性向量两者间的联合信息量，更有利于全面地捕捉符号网络隐含的特征信息。

3.2 局部符号信息拟合

1) 模型构建

使用P维向量xi∈RP作为节点vi∈V的局部符号向量表示，不同节点vi与vj之 间的相似度P(vi,vj)为：

式中， σ是sigmoid 函数。

基于结构平衡理论，最大化正关系节点间的相似度，并最小化负关系节点间的相似度，目标函数构造为：

式中，sij∈{1,-1}。

通过最大化式(5)，就可以得到节点vi的局部符号特征的k维向量表示xi。

2) 节点对采样

在这里，SNSH 拓展了传统的负采样策略，依据边的类型，在相应集合中选取负采样节点，以使其适用于符号网络。如对于sij=1的正关系节点对，该方法从节点vi与vj的 负邻居集及进行采样，来最大化节点vi与vj之间相对于其负邻居集中节点的相似度。同理，对于sij=-1的负关系节点对，从节点vi与vj的 正邻居集及进行采样，来最小化节点vi与vj之间相对于其正邻居集中节点的相似度。因此，基于条件独立假设和特征空间的对称性假设，可以为每个节点构造目标函数：

式中，sij=1；siu=-1； σ是sigmoid 函数。

3) 模型优化

为了方便计算，改进了传统的负采样方式，每次仅优化一对节点及确定数目的负样本。同时采用定义虚拟节点的方法，解决了部分节点不存在负样本的问题。

本模块采用了创新的负采样方式，基于词向量模型及结构平衡理论，对符号网络中的正负关系进行了拟合，最终得到了可以体现符号网络特性分布的p维节点嵌入矩阵X，供后面使用。

3.3 网络结构拟合

在该部分使用一个节点嵌入编码器ε=RN×P×RP×d→RN×d来进行网络结构拟合。模型的输入是节点的局部符号信息拟合向量xi∈XP，目标是生成d维节点嵌入矩阵H(用hi来表示矩阵H的第i行向量)以及概括向量s。该编码器是一个单层的GCN：

使用拟合符号结构后的节点嵌入作为GCN 的输入，而非重新定义GCN 的传播模式，并引入ω1,ω2∈R来 控制自连接的权重。较小的 ω1或 ω2表明，节点本身在生成其嵌入中起着更重要的作用，这也意味着降低了其邻居节点的重要性。对于正关系和负关系给予不同的权重，以拟合它们在传播中对邻居的不同影响。

编码器产生的hi嵌 入了以节点vi为中心的网络的区域特征，而不仅仅是节点本身。为了得到网络级别的概括向量s，使用函数RN×d→Rd，通过聚合节点特征的方式来得到整图的特征表示，函数定义为：

3.4 特征属性向量构造

传统方法使用节点的入度、出度、地位、建立正向边趋势等属性对边符号进行预测[39]，实验表明，这些节点的特征属性对节点的特征学习是有意义的，但它们往往在符号网络表示学习方法中被忽略。对节点vi∈V，其特征属性向量fi∈F表示为：

式中， dei代 表节点vi的 度；分别表示节点vi的 正关系邻居数以及负关系邻居数； pri表示节点vi建立正向边的趋势，其计算方法为：

3.5 高阶互信息估计

对于符号网络中的节点，使用最大化高阶互信息来综合考量3 类变量，分别是节点嵌入hi、网络的概括向量s和节点的特征向量fi。

根据高阶互信息的定义，当N=3，有：

该式可进一步化为：

式中，I(X1;X2,X3)表 示变量X1同 变量X2,X3的联合分布之间的互信息。通过使用hi，s和fi替 代X1，X2，X3，可以得到式子：

式中，I(hi,s)捕获外部信息量，即节点局部嵌入h与全局嵌入之间s的依赖；I(hi,fi)捕获内部信息量，即节点局部嵌入h与节点本身特征属性向量f之间的依赖；I(hi;s,fi)捕获联合信息量，即外部和内部信息量之间的交互。即通过外部信息量、内部信息量和联合信息量三者，可以衡量网络的高阶互信息，这3 个信息量的嵌入过程如图3 所示。在高阶互信息最大化模块，将依次进行目标函数的构造。

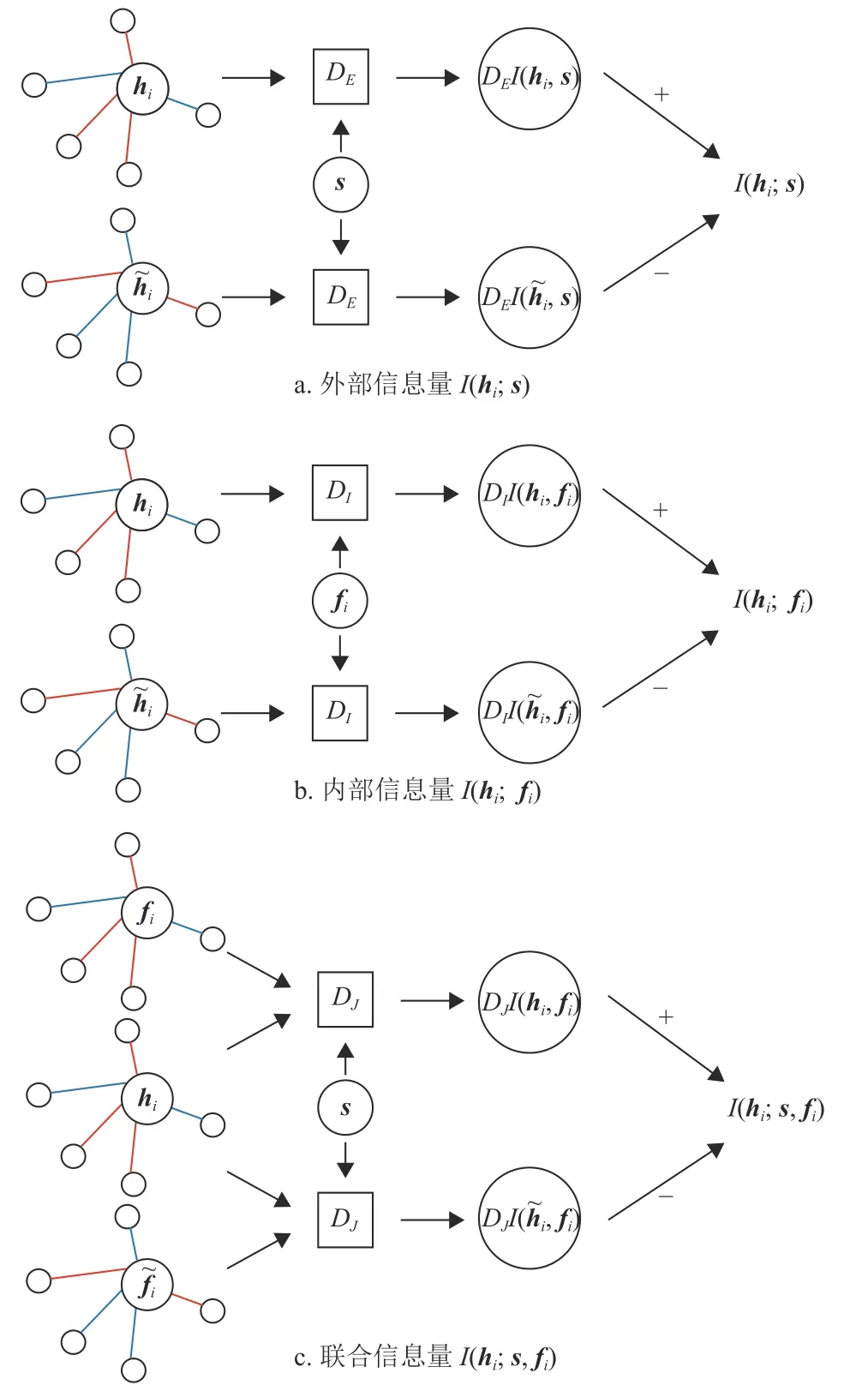
图3 外部、内部和联合信息量示意图

3.6 高阶互信息最大化

通过最大化局部互信息来捕获整个网络的高阶信息量。根据式(13)，最大化高阶互信息等同于最大化3 种局部互信息：

接下来，给定节点嵌入矩阵H、概括向量s及其特征属性向量矩阵F，最大化式(13)中的3 种信息量来对参数进行优化，最终目标函数为下：

式中， λE， λI和 λJ是训练参数。

分别计算3 种信息量的交叉熵，外部信息量I(hi;s) 对 应的交叉熵LE为：

内部信息量I(hi;fi) 对 应的交叉熵LI为：

联合信息量I(hi;s,fi) 对 应的交叉熵LJ为：

式中，hi和分别是图G的正节点嵌入和负节点嵌入。

同时，对于联合信息量，去除了在外部和内部信息量中所捕获的信息，因此仅对属性向量取反。

DE，DI，DJ分别是3 种表示对分数的鉴别器，本文参考HDMI，应用了一个简单的双线性评分函数：

4 实验与分析

4.1 实验数据集

为了研究符号网络中的学习表示，选取了4 个真实的符号网络数据集进行实验，即Bitcoin-Alpha，Bitcoin-OTC[40-41]，Slashdot[42]和New Guinea，表1列出了相关数据集的统计信息。

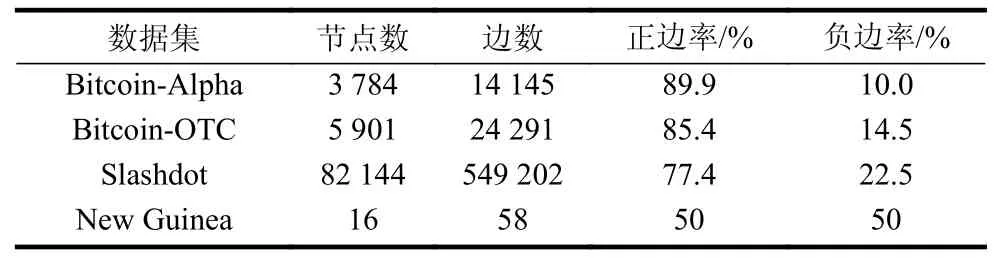
表1 实验数据集统计信息

Bitcoin-Alpha 和Bitcoin-OTC 数据集都来自支持比特币消费的开放市场，由于比特币账户的匿名机制，网站出于安全考虑建立了在线信任网络，用户可以选择对他人信任或不信任。Slashdot 是一个技术新闻网站，用户之间可以创建双向的好友或敌人关系，代表他们对彼此之间的态度。New Guinea是一个拥有16 个节点的数据集，表示新几内亚中部高地16 个部落之间的关系。

以上4 个数据集，都是符号网络研究领域的经典数据集，比较具有代表性。对于这些数据集中的网络，本文忽略其中的链接方向，统一将其视为无向网络进行研究。

4.2 链接符号预测描述

链路符号预测问题，即给定符号网络中存在的一组链接，将其排除在训练集之外的同时，希望能预测出它们在节点对之间的符号正负性。

为此，训练了一个二分类器，该分类器根据一对节点的输入特征集来预测其对应的符号 (本文使用逻辑回归模型)。本文将两个节点的最终嵌入向量直接相连来作为模型的输入，并利用训练数据中边的标签对模型进行训练。鉴于数据集中正链接数远多于负链接数，同时使用F1 与AUC 两种指标来评估算法的效果，更高的F1 及AUC 都意味着更好的性能。对于每个数据集，随机选择50%的数据作为测试集，其余50%作为训练集。

4.3 链路符号预测效果分析

为了验证本文提出算法的有效性，选择了DeepWalk[19]、LINE[24]、SNEA[29]、SGCN[28]、SDGNN[30]这5 个算法，来与SNSH 算法在链路符号预测任务上进行对比实验。在评估SNSH 算法的性能时，将局部符号信息嵌入和高阶互信息嵌入拼接以作为线性模型的输入特征，另外，测试了仅考虑其中一种额外信息量时模型的效果，分别为SNSH-E、SNSH-I、SNSH-J，其实验结果如表2 和表3 所示。在该部分，选取Bitcoin-Alpha、Bitcoin-OTC 和Slashdot这3 个数据集，用以进行实验效果的分析对比。

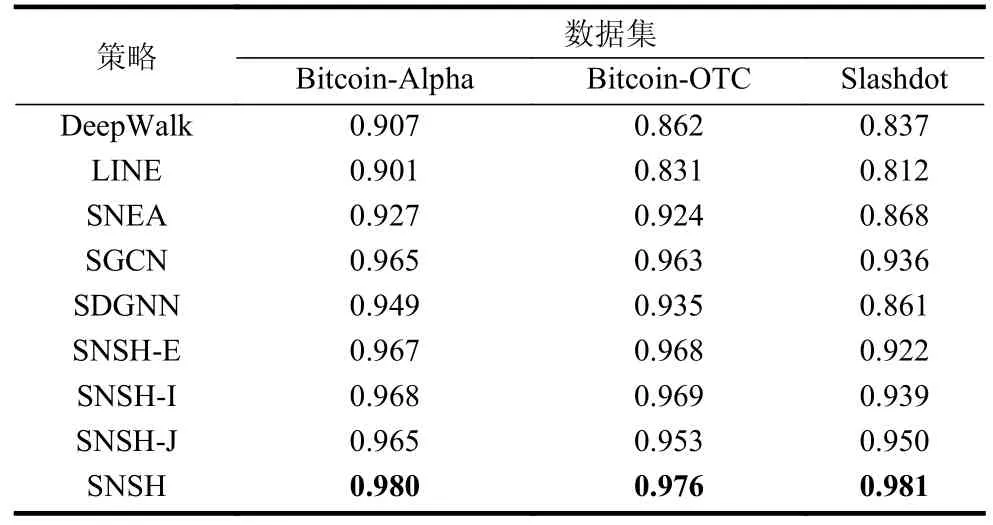
表2 F1 衡量的链路符号预测任务算法效果对比

F1 分数是用来衡量二分类模型精确度的常用指标，是模型精准率和召回率的调和平均，由于真实符号网络中绝大部分都是正向边，因此所有算法得到的F1 分数都较高，但本文算法还是在所有数据集上取得了最好的效果。

在AUC 指标上，SNSH 同样获得了最好的性能。同时可以看到，针对3 个中大型符号网络数据集，SNSH 算法的实验结果稳定，F1 指标分别为0.980、0.976、0.981，AUC 指 标 分 别 为0.921、0.916、0.871，显示了算法良好的稳健性。

实验表明，本文方法在所有指标与数据集上取得了最佳的效果。并且，仅考虑单一信息量的SNSH模型也取得了超过现有算法的效果。这证明本文选取的信息量，能够有效提取到真实网络中的额外信息。SNSH 算法能高效地拟合真实符号网络中的信息，从而得到有效的向量表示。

4.4 算法合理性分析

为了衡量算法对网络真实结构的拟合效果，接下来进行验证分析SNSH 学习的嵌入空间是否遵循结构平衡理论的原理。

分别使用LINE、SGCN 与SNSH 算法对New Guinea 网络的拓扑结构进行嵌入来进行效果分析。具体来说，分别将网络作为算法的输入，经过训练得到了数据集在网络嵌入后的二维表示，其绘制结果分别如图4、图5、图6 所示。

图4 LINE 二维嵌入效果示意图

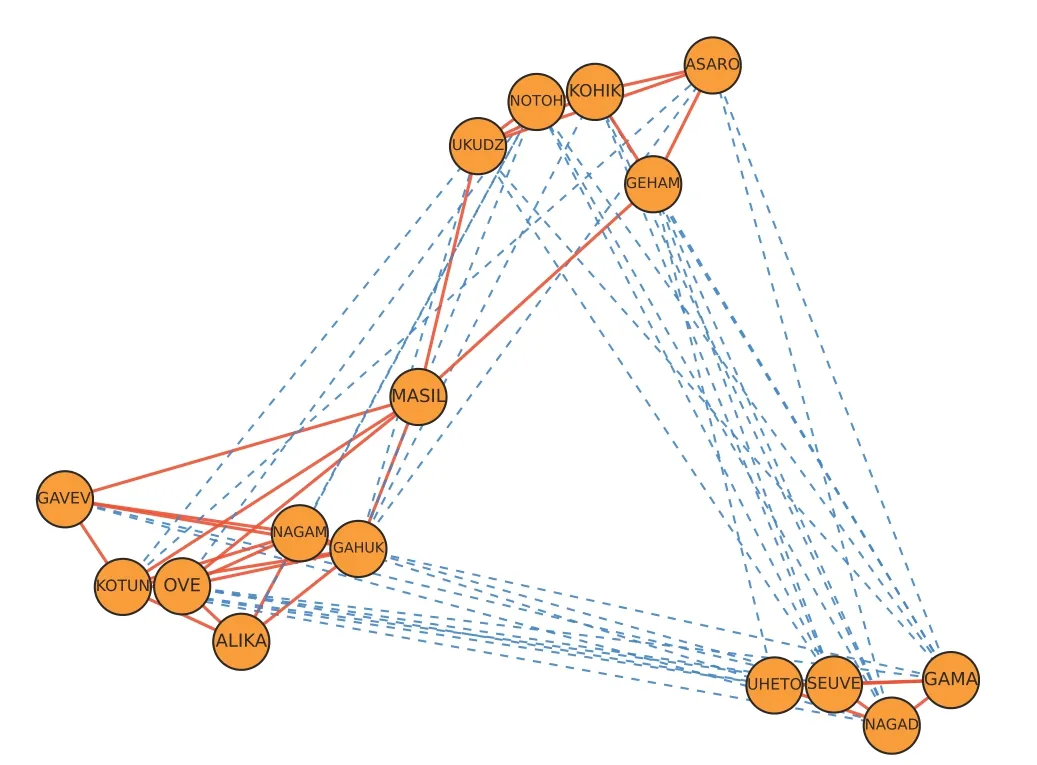
图5 SGCN 二维嵌入效果示意图

在示意图中，网络中的正边用加粗表示，负边用虚线表示。在由LINE 算法得到的图4 中，节点分布杂乱无序，不符合符号网络的特征。相对而言，从考虑了符号网络特性的SGCN 算法与SNSH算法得到的图5 和图6 可以看出，代表正关系的线条普遍较短，代表负关系的线条普遍较长。这表明具有正边关系的节点在二维空间上是接近的，而具有负边关系的节点在二维空间上是疏远的，更符合符号社会网络的特征，且能与社会结构平衡理论的观点相印证，即节点的“朋友”比节点的“敌人”更近。

在图5 和图6 的对比中，由SNSH 算法得到的图6 拥有更清晰合理的网络节点布局，在部分节点上优于SGCN。可以说，SNSH 算法更好地拟合了数据集的真实结构，这体现了算法的合理性与解释性。因此，SNSH 所学习到的嵌入是符合结构平衡理论和符号网络真实情况的。本文使用的实验数据、相关源代码和算法的描述等内容详见链接：https://github.com/amoius/SNSH。

5 结 束 语

针对现有网络表示学习领域中符号嵌入方法的缺失与嵌入深度的局限性，本文提出了一种基于结构平衡理论与高阶互信息的符号网络表示学习方法SNSH，来对符号网络中的隐藏信息进行更深层的挖掘。在不影响甚至提高准确率的情况下，对符号网络的内部、外部及联合信息进行了捕捉，从而得到符合符号网络特性的节点嵌入。在3 个真实数据集上进行了链路符号预测性能的对比实验，并在New Guinea 数据集上进行了可视化实验，验证了本文所提模型具有较高的有效性与合理性。未来计划将算法拓展到复合符号网络表示学习等问题的研究中。