量子近似优化算法在投资组合优化中的应用

吴涵卿，袁淏木，陈柄任，吴 磊，李 鑫，李晓瑜

(1.建信金融科技有限责任公司 上海 浦东区 200120；2.四川元匠科技有限公司 成都 611730；3.电子科技大学信息与软件工程学院 成都 610054)

近年来，量子计算所获得的各领域的关注与日俱增[1-2]。然而，容错(fault-tolerant)量子计算机在近期出现的可能性仍然较低[3]。因此，近期能够真正付诸实际应用的量子计算算法将主要围绕中等规模噪声量子(noisy intermediate-scale quantum,NISQ)计算机展开。大部分NISQ 计算机上的算法都是经典-量子混合的，这类算法将待解决问题中经典计算机上计算较为困难而适合量子计算完成的部分交由量子计算机完成，而其他部分仍然由经典计算机完成。这类算法通过经典计算机上的优化方法，不断迭代含参量子线路中的参数以得到优化后的量子线路，进而得到所期望的量子态，因而被称为变分量子算法(variational quantum algorithm, VQA)[4]。

在VQA 中，文献[5]提出的量子近似优化算法(quantum approximation optimization algorithm,QAOA)能够高效解决具有特定特征的无向图上最大割(max-cut)问题。这一问题在经典计算机上是NP 完备的[6]。文献[7]在其基础上提出了量子交替算子拟设(quantum alternating operator ansatz,QAOA)，通过对量子线路上算子结构的不同设计，将文献[5]提出的近似优化算法拓展到有关字符串、排序和流程规划的一系列问题上，因而可以视作前者的拓展。本文将二者及在其之上进一步衍生的这一类算法统称为量子近似优化算法，并在下文以QAOA 指代。

目前，除了QAOA 之外，还有运用其他类型的量子算法进行投资组合优化的研究。如文献[8]提出了基于HHL 的最优化均值-方差模型的方法，这一方法经文献[9]的拓展，可以解决任意数量的整数约束和预算约束下的均值-方差模型下的投资组合优化问题。文献[10]提出了NISQ 硬件条件下HHL 解决投资组合优化问题的方法。这些基于HHL 的投资组合优化方案所考虑的解空间是连续的，而非QAOA 所关注的离散化模型。由于HHL 的关键要素QRAM 的高效实现仍待探索[11]，因而基于HHL 的投资组合优化算法相较在NISQ时代的实际应用仍有一定的距离。文献[12]提出了基于Grover 搜索算法的投资组合优化方案，其考虑的问题与下文中介绍的投资组合优化再平衡模型相同，这一方案的优点在于量子线路的设计清晰简洁，可解释性强。然而，该算法对于均值向量和协方差矩阵中非整数的系数按比例使用整数近似，受限于NISQ 时代较少的量子比特数，面对非整数参数的投资组合优化问题存在着精度不足的瓶颈。另一方面，利用量子退火进行投资组合优化也是许多研究关注的重点，如文献[13]对于反向量子退火在投资组合优化中的应用的研究以及文献[14]对于量子退火中的控制对于无约束组合优化问题求解的影响。量子退火由于其对应的硬件发展较为成熟、规模较大，因此在近期有可能展现量子计算相较经典计算的优势，但其所能带来的效率提升如何却仍待探索[15]。此外，亦有利用量子随机游走进行投资组合优化的研究[16]，其实际上属于QAOA 的一种变体。总而言之，QAOA 对于本文所关注的NP 难的离散投资组合优化问题有着精度更高、更可能在NISQ 时代付诸实际应用的优点。

1 均值-方差模型

1.1 马科维茨的均值-方差模型

均值-方差模型[17-18]是金融学中最经典的模型之一。假设投资者有n个备选资产，其收益率均为随机变量。这些资产的期望收益率向量为μ=((μ1,)μ2,···,μn)T∈Rn， 收 益 率 的 协 方 差 矩 阵 为Σ=σi j∈Rn×n。 投资者可以对这n个资产进行加权组合。记其在第i个资产上的投资份额为xi，则该投资组 合 的 向 量 表 示 为x=(x1,x2,···,xn)T∈Rn。相 应地，该投资组合的期望收益为 μTx， 方差为xTΣx。投资者希望在给定期望收益 μ0∈R时，最小化投资组合的方差，于是可作如下优化：

由于协方差矩阵一定是半正定的，因此，式(1)可在经典计算机上以多项式时间复杂度的算法解决。

式(1)的一个等价形式如下[19]：

式中， η ∈[0,1]； 1 =(1,1,···,1)T。 η代表了投资者在风险和收益二者间的权衡情况，称为权衡系数。显然，当η =0时，投资者只关注收益，倾向于选择最为激进的投资组合；而当η =1时，投资者只关注方差，倾向于选择最为稳健、方差最小的投资组合。

1.2 均值-方差模型的离散化

1.3 投资组合再平衡问题

投资组合再平衡(Rebalancing)问题[20]是式(3)的拓展。在再平衡问题中，投资者在决策前已经有一定的持仓y=(y1,y2,···,yn)T。在单笔交易成本T≠0 的 情况下，式(3)相当于y=(0,0,···,0)T的特殊情形，而一般情况下， ∃i,yi≠0。于是，就有了本文剩余部分所关注的模型：

显然，这一问题仍旧是NP 难的。

2 QAOA 的投资组合优化建模

2.1 QAOA 的基本框架

QAOA 将原问题的可变向量映射为量子比特的张量积，经量子线路变换后，将逆映射作用于测量结果得到特定条件下近似最小(大)化目标函数的可变向量取值。以最小化问题为例，QAOA 的基本框架如下。

1)设投资者需要最小化的目标函数为可变向量z的函数f(z),z∈Rn。则需要构造合适的映射φ(·)，φ(z)=|φ〉,〈φ|φ〉=1， 并确定目标函数对应的哈密顿量C，使得f(z)=〈φ|C|φ〉。

4)通过经典计算机上的优化算法(如梯度下降法)，不断迭代更新参数 γ ,β。每次迭代计算得到新的 γ ,β值之后，重复步骤3)，将新参数下的演化算子作用于初态 |φ0〉，测量末态并计算出新的函数值，进而利用新的函数值算出下一步迭代的 γ,β，直至算法收敛为止。此时，算法得到最终的一组参数γ*,β*及其对应的演化算子U(γ*,β*)。

2.2 投资组合优化问题的QAOA 建模

为形式统一，可以变换式(4)中的交易成本项，得到：

则最小化式(4)中的f(z)等价于最小化：

对于任意zi,i∈{1,2,···,n}， 将其映射到si1,si2两个量子比特的张量积 |si1〉⊗|si2〉 上 ，即φ(zi)=|si1〉⊗|si2〉。令：

具体地，zi和si1,si2的映射关系如表1 所示[20]。

表1 zi 和 si1,si2的映射关系

此外，本文约定φ-1(|1〉⊗|1〉)=0。

考虑泡利-Z 矩阵(Pauli-Z matrix)：

那么由于：

有关系式zi=〈φ|Ci|φ〉。 因此，目标函数g(z)对应的哈密顿量为：

自此，本文构造完成了上一节步骤1)所需的对应关系，得以进行QAOA 的后续步骤。

3 利用QAOA 进行投资组合优化的不同方法

3.1 软约束下的标准QAOA

文献[5]提出QAOA 时所选定的初态为均匀叠

文献[20]的实验结果显示，软约束下的标准近似优化算法解决投资组合优化问题的效果相较经典穷举法(brute-force search)没有明显的优势，因此本文的数值模拟将不涉及该方法。

3.2 软约束下的热启动QAOA

对于最大割等整数优化问题，在经典计算机上，可以采用随机取整(randomized rounding)[23-24]的方法，利用放松原问题的整数约束进行优化所得到的结果寻找整数约束下的最优解。相应地，也可以利用放松整数约束的经典优化结果设计QAOA初态，这种方法被称作热启动[25](warm-starting)。对于式(4)，记：

令：

则s1,s2∈[0,1]n，z=s1-s2。求解：

则软约束下热启动的初态：

相应地，算法使用混合算子U(BSWS,βk)，其中：

当 si=1或 si=0 时 ，BWS仅能在相位的意义上改变相应的量子比特。为了避免出现诸如放松整数约束时的最优解和原问题恰好分别为0 和1 的情形，令：

混合算子U(BSWS,βk)并不能保证优化过程在HD下进行，因此本节引入3.1 节所述的惩罚项A(1Tz-D)2对优化过程进行约束。因此，本文称本方法为软约束下的热启动QAOA，在下文用SWSQAOA 指代。

3.3 软约束下的连接热启动QAOA

3.2 节中的混合算子U(BSWS,βk)均由单比特门构成，并没有考虑不同量子比特之间的相关性。因此，一个自然的想法便是在混合算子中引入不同量子比特的相互作用因素。可以构建连接混合算子U(Bcop,βk)[26]，其中：

本文约定n+1 ≡1,n+2 ≡2。是有关参数t∈[-1,1]的 量子门操作，其中t代表不同量子比特之间的相关性，同 γ ,β相同，由经典优化算法确定最优值。自此，本文得到了软约束下使用连接混合算子的热启动QAOA，在下文用SX-QAOA 指代。

3.4 硬约束下的标准QAOA

另一种解决使用X-混合算子时容易得到非可行解的方法是修改混合算子的设计。XY-混合算子[22]U(BXY,βk)能 够使得只要初态| φ0〉∈HD，近似优化算法一定在 HD内进行，因而能够显著地减小算法最小化目标函数的搜索范围。

在两类主要的XY-混合算子中，全连接(complete-graph)XY-混合算子[22]考虑了所有可互相交换(即交换后，量子态所对应的资产组合不违背约束条件)的两个量子比特，在投资组合优化问题的背景下，即：

而环形XY-混合算子(ring mixer)[20,22]仅考虑了相邻的可互相交换的两个量子比特。尽管前者在实现效率上较后者略低，但由于其优化效果更好[22]，因此本文选用完全图XY-混合算子作为硬约束下的混合算子。

4 数值模拟及分析

4.1 数据及参数介绍

本文基于股票收益率和协方差数据进行数值模拟，比较不同QAOA 方法求解投资组合优化式(4)的效果。模拟所使用数据为由2021 年第3 季度A 股3 847 支股票(已剔除单日收益率大于20%及含有缺失值的股票)日收盘价计算得到的日均收益率及收益率协方差数据。

对于p=1,2,3,4的不同情形，本文分别进行1 000次数值模拟。每次数值模拟，均从3 847 支股票中随机抽取12 支股票，将其日均收益率及收益率协方差矩阵代入式(4)，并分别用经典穷举法、SWSQAOA、 SX-QAOA 及H-QAOA 进行求解。如图1所示，在参数设置方面，本文根据一定的分布随机生成参数y, λ,D的 值。记第m∈Z+次模拟中，参数y, λ,D的 取 值 分 别 为ym=(ym1,ym2,···,ym12)T，λm,Dm，则：

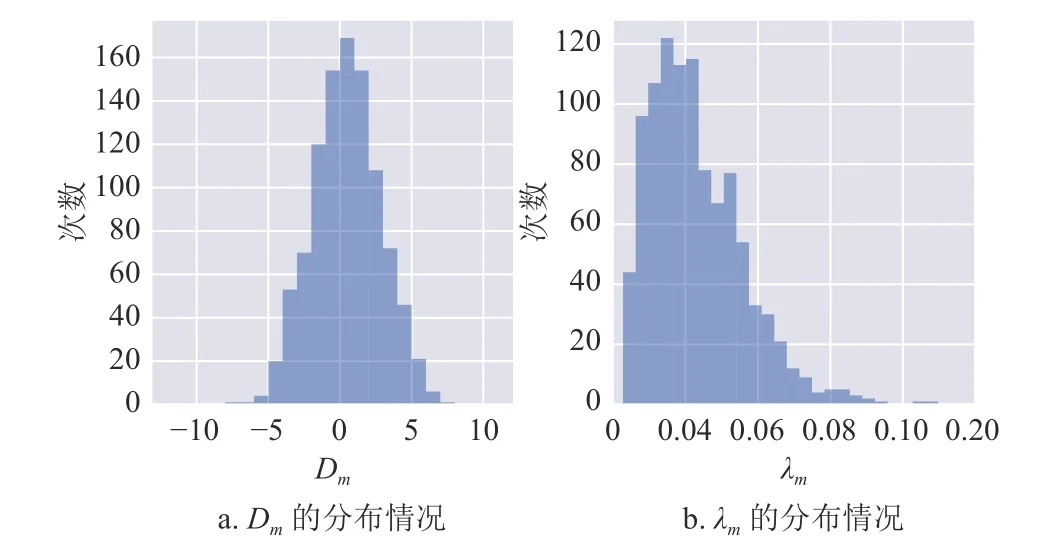
图1 D m 和 λm的分布情况

此外，本文令 γ,β 的初值均为p维 0 向量，t的初值为0.2，并设置m1=m2=1000, ϵ=0.25[25]，惩罚项A=50， 交易成本T=0.14。

4.2 数值模拟结果分析

本文从近似比(AR)和成功比例(SR)两个角度比较不同QAOA 方法的效果。对于第m次实验，某QAOA 方法的近似比A Rm的定义为：

其中：

而在1 000 次实验中，某QAOA 方法成功比例 SR的定义为：

即该QAOA 方法成功找到全局最优解的次数比例。

数值模拟的近似比情况如图2 所示，不同近似比结果的累计密度如图3 所示。

图2 各方法的平均近似比

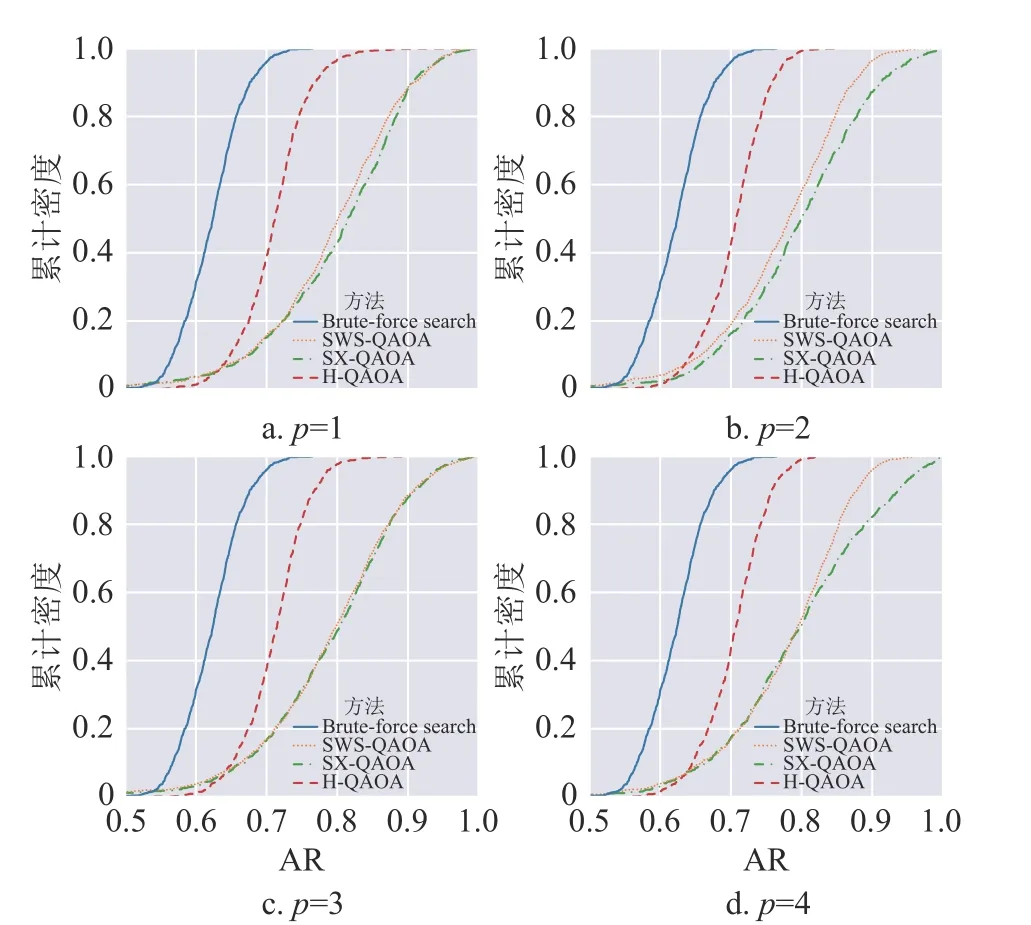
图3 各方法的近似比的分布

图中所涉及4 种方法按近似比从高到低排序分别为SX-QAOA、SWS-QAOA、H-QAQA 及穷举法，各量子算法较经典穷举法均有至少7%的提升。为了进一步确定不同方法的效果是否有显著差异，本文基于中心极限定理(central limit theorem)[27]，假定4 种方法近似比的均值均服从正态分布，对其差异进行双边t检验。本文取上、下临界值分别为相应t分布的97.5%分位数和2.5%分位数。假设检验结果如图4 所示，可以认为t统计量高于上临界值说明该组前一方法的平均近似比显著高于后一方法，若低于临界值说明该组前一方法的平均近似比显著低于后一方法。其他情况意味着该组的两种方法的平均近似比差异不显著。

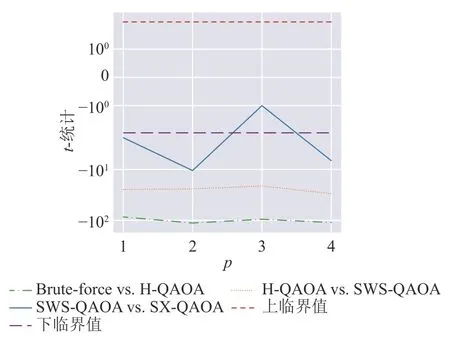
图4 各方法平均近似比差异的假设检验结果

可见，除p=3时SWS-QAOA 和SX-QAOA 的平均近似比差异不显著之外，其余11 组假设检验结果均显著。本文进一步确定了在近似比的意义上各方法均存在显著差异。量子算法相较经典穷举法在平均近似比上均有着显著的提升，其中SX-QAOA表现最优。

3 种不同QAOA 方法的成功比例情况如图5 所示。

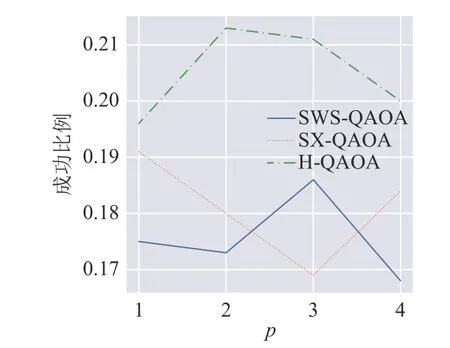
图5 各方法的成功比例

直观上看，若将3 种QAOA 方法按照成功比例从高到低排序，则最高的为H-QAOA，但SWSQAOA 和SX-QAOA 较难区分高低。与之前类似，本文进行各方法成功比例差异的双边t检验，以判断其是否显著。结果如图6 所示。

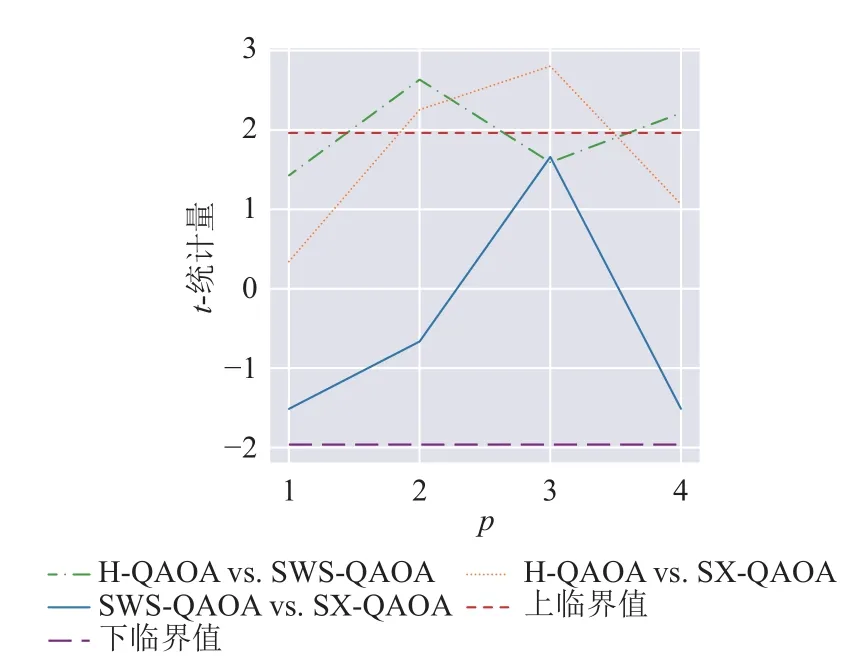
图6 各方法成功比例差异的假设检验结果

可见，仅在p=2及p=4时，H-QAOA 的成功比例显著高于SWS-QAOA 的成功比例；在p=2及p=3时，H-QAOA 的成功比例显著高于SX-QAOA的成功比例。而其余组假设检验的结果均不显著。因此，本文认为，在成功比例的意义上，H-QAOA略优于SWS-QAOA 和SX-QAOA，但后二者之间难分伯仲。

5 结 束 语

本文对于QAOA 在投资组合优化中的应用从理论建模、不同方法及数值模拟等多角度进行了详细的讨论。针对未来相关领域的研究，本文有如下两点展望。

1)回顾前面介绍的各种利用QAOA 进行投资组合优化的方法，可以注意到，软约束QAOA 能够利用放松整数约束的经典优化结果进行热启动，起到类似经典算法中随机取整的效果。然而，软约束QAOA 搜索空间是全状态空间，而满足约束条件的子空间 HD仅仅是其中的一个超平面。随着n的增大，软约束QAOA 所搜索的空间将几乎全是非可行的冗余状态。因此，在测量次数m1,m2不变的情况下，随着n的增大，软约束QAOA 很可能将逐渐失效。另一方面，现有的硬约束QAOA 尽管将搜索空间缩小至 HD内，但是并未利用经典优化的结果进行初态设计，存在进一步提升的可能。如何将放松约束的经典优化结果与硬约束的QAOA结合起来将成为一项有价值的课题。

2)从数值模拟结果来看，各QAOA 方法的近似比和成功比例并未随着p的增大而单调递增，这表明更加复杂的模型并没有带来更好的表现。此外，各QAOA 方法的成功比例均为20%左右，搜索得到全局最优解的概率并不高。导致QAOA 表现不及预期的原因很可能是QAOA 的经典优化过程中常见的所谓贫瘠高原(barren plateau)问题[4,28]以及QAOA 本身存在的可及性缺陷(reachability deficits)问题[29]。前者往往使得经典优化算法提前终止，进而导致QAOA 无法找到理论最优值 |φ*〉；而后者表明，即便找到了 |φ*〉，但可及性缺陷仍然可能较大，这意味着使用某些演化算子的QAOA的效果可能存在着无法逾越的理论上限。如何针对投资组合优化问题设计更加合适的演化算子以解决这些问题亦将是一项富有意义的工作。