Latin 方阵和二维量子漫步相结合的图像加密

蒋建伟，张 田，陈祯羽，马鸿洋*

(1.青岛理工大学信息与控制工程学院 山东 青岛 266520；2.青岛理工大学理学院 山东 青岛 266520)

随着互联网与多媒体技术的快速发展，信息的安全性问题日益凸显。数字图像作为信息传输的主要载体之一，如何有效地保护图像的信息不被窃取是当今的一个热门研究课题。保护图像信息安全的方法主要分为两类：图像加密[1-5]和图像水印[6-9]。图像加密的原理是针对图像的像素点的位置和像素值按照特定的方式做出改变，从而在变换之后的图像上无法获取原图像的数据信息；图像水印是通过把图像嵌入载体图像以此来达到隐藏图像信息的效果。如今的图像加密技术已经发展得比较成熟，其中主流的加密方法有： DNA 编码加密[10-12]、混沌系统加密[13-15]、魔方置乱加密[16-18]、 Arnold 置乱变换[19-22]等。

Arnold 置乱变换是在研究遍历理论时提出的一种变换方法。由于Arnold 置乱变换最初的实验对象是猫的图片，所以Arnold 置乱变换也叫作“猫脸变换”。Arnold 置乱变换是一种在有限区域内进行反复折叠和拉伸变换的置乱方法，凭借其置乱直观、具有周期性等多种优点，经常与混沌系统相结合被用于图像加密。文献[23]在Arnold 置乱变换和混沌系统的基础上，设计了一种以彩色图像为载体的抵抗几何攻击的数字水印方案。该算法可以有效地解决图像质量和鲁棒性之间的冲突问题。文献[24]提出了一种基于Arnold 置乱变换和Hardmard 单像素的彩色图像加密算法。该加密算法只需要一个桶形探测器就可以对彩色图像实现成像质量好、安全性能高的加密效果。

近年来，量子计算与量子通信飞速发展，为许多经典算法难以有效解决的难题提供了新的思路以及发展方向。量子随机行走是经典随机行走与量子计算相结合而生成的。量子随机行走已与多种经典算法相结合，存在于许多加密以及搜索算法中[25-28]。量子随机行走相比于经典随机行走主要有两方面的优势：1)量子随机行走具有量子计算的并行性特点，因此它有着更快的运行速度；2)量子随机行走有着更大的密钥空间，如果把量子随机行走应用于加密算法中，能使加密算法中的随机序列有更强的随机性，加密图像从而可以更好地抵御暴力攻击。文献[29]设计了一种基于量子漫步和离散余弦变换的彩色图像加密方案，利用量子漫步的控制参数替代随机掩膜来作为加密过程中的密钥，有利于密钥的管理与传输。文献[30]将量子漫步与双随机相位编码技术相结合，提出了一种新型图像加密技术，量子漫步被用来在双随机相位编码的过程中生成随机掩码。

Latin 方阵是一种特殊的方阵，它的每一行或每一列中的元素各不相同，但是每一行以及每一列中的元素种类是相同的。Latin 方阵具有直方图均匀、密钥空间大等诸多优点，在图像加密方面有很大优势[31-33]。文献[34]将Latin 方阵与混沌系统相结合研究出了一种图像加密方案，该加密算法利用Latin 方阵与混沌系统的同质性使得方案本身具有更好的混淆和扩散效果。文献[35]设计了一种新型的图像加密方案：首先利用混沌系统生成随机序列，再利用两个随机序列生成Latin 方阵，然后用Latin 方阵以及随机矩阵完成像素值替代，从而完成图像加密。

本文将Arnold 变换与Latin 方阵、量子漫步相结合，设计了一种新型的图像加密方式。其中Arnold 变换和Latin 方阵用来对图像进行处理，然后对置乱之后的图像使用加取模扩散方法进行像素值的变换。解密过程为加密过程的逆过程。

1 相关工作

1.1 Arnold 置乱变换

Arnold 置乱变换被定义为：

式中， αn, βn表示变换前图像中的像素点坐标；αn+1和 βn+1表示经过变换之后图像的像素点坐标；N表示图像的长度；n表 示当前所变换的次数；x,y为参数(本文采用x=y=1)。在图像解密时，可以用Arnold 反变换(这里 α=β=1)，反变换的公式为：

Arnold 置乱变换的原理如图1 所示。

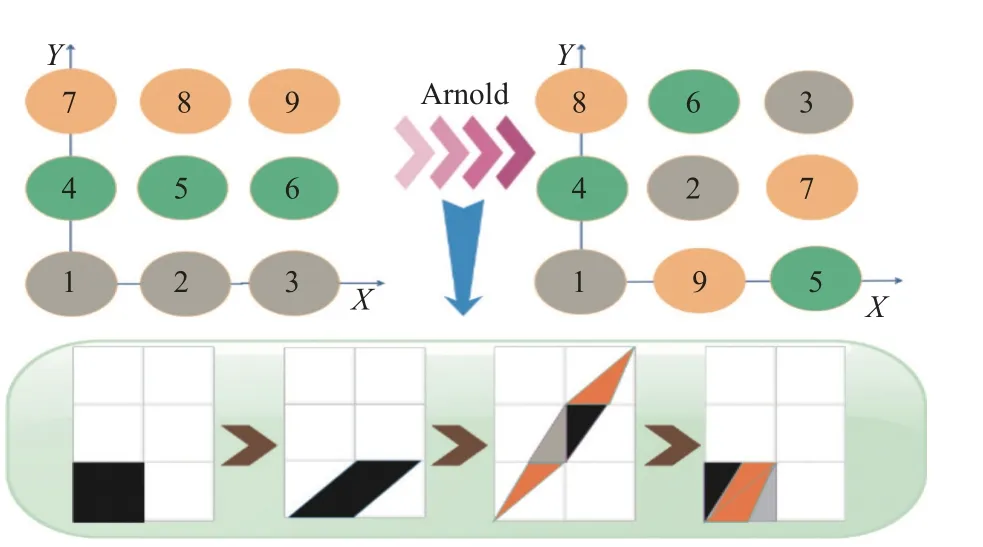
图1 Arnold 变换原理图

1.2 量子漫步

量子漫步是量子计算中的一个重要模型。如今量子漫步有连续量子漫步和离散量子漫步两种计算模型，本算法利用的是离散时间量子漫步。离散量子漫步是经典漫步与量子计算结合而来的。离散量子漫步在经典漫步的基础上引入了硬币态的概念，它的每步行走由硬币态控制操作和偏移操作共同决定。首先进行硬币态操作，再由硬币态的输出来决定下一步如何移动。而量子漫步的希尔伯特空间由粒子的位置空间与硬币空间张量而成，故量子漫步的动态演化可以看作是一个酉算符反复作用到叠加态上，其中酉算符可以表示为：U=SC，其中，S为偏移算子，C是硬币算符。

本文采用Hardmard 算子作为硬币算符，S作为偏移算子。当硬币态为0 时，位置态将前进一步；反之当硬币态为1 时，位置态将后退一步：

在二维空间内的交替量子漫步中，如图2 所示，偏移算子可看作两部分组成：X轴方向上的偏移算子和Y轴上的偏移算子：

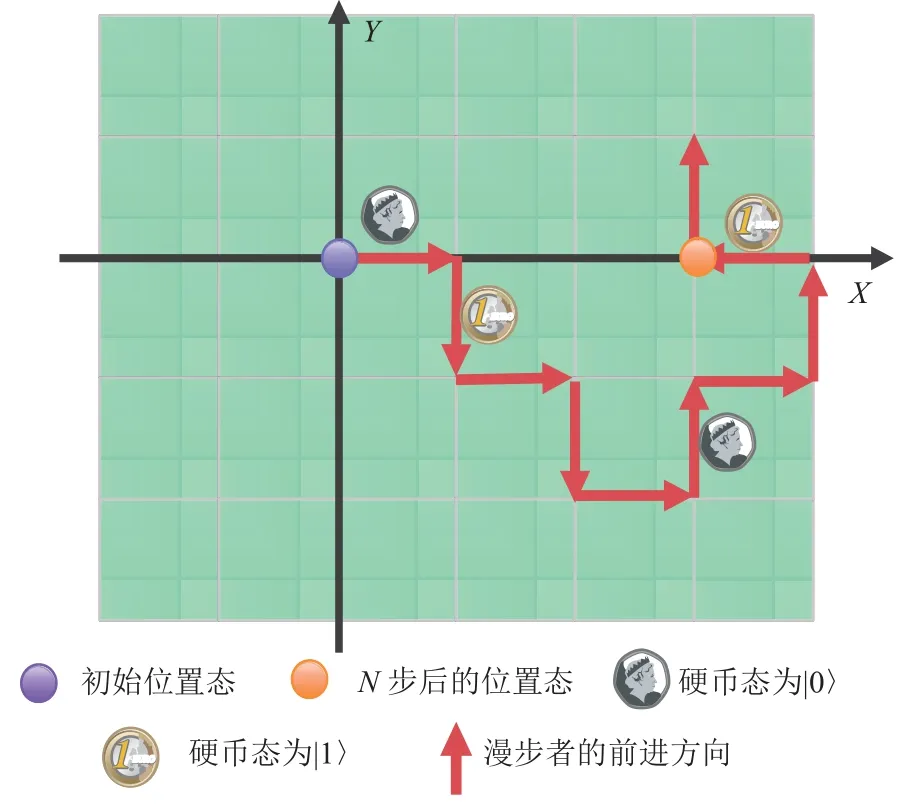
图2 量子漫步原理图

假定交替量子漫步的初始态为 | ψ0〉，则在N步行走之后的叠加态为：| ψN〉=UN|ψ0〉。

根据漫步在位置(x,y)的概率大小得到概率矩阵：

1.3 Latin 方阵

对于一个n阶方阵A=(ai,j)n×n，如果该方阵正好有n种不同的元素，并且每一种元素在同一行或同一列里只出现一次，那么这种方阵称作Latin 方阵。Latin 方阵在图像加密中具有促进像素值的均匀分布，平衡图像矩阵中的像素值的作用。图3a～图3d 分别对应3～6 阶Latin 方阵。

图3 Latin 方阵

2 算法流程

该算法的加密过程分为4 个过程：1) Arnold变换；2)利用量子漫步生成随机序列从而生成Latin 方阵；3)由Latin 方阵和两个随机矩阵生成与图像矩阵做异或操作的密钥矩阵；4)对图像进行加取模扩散处理。如图4 所示。

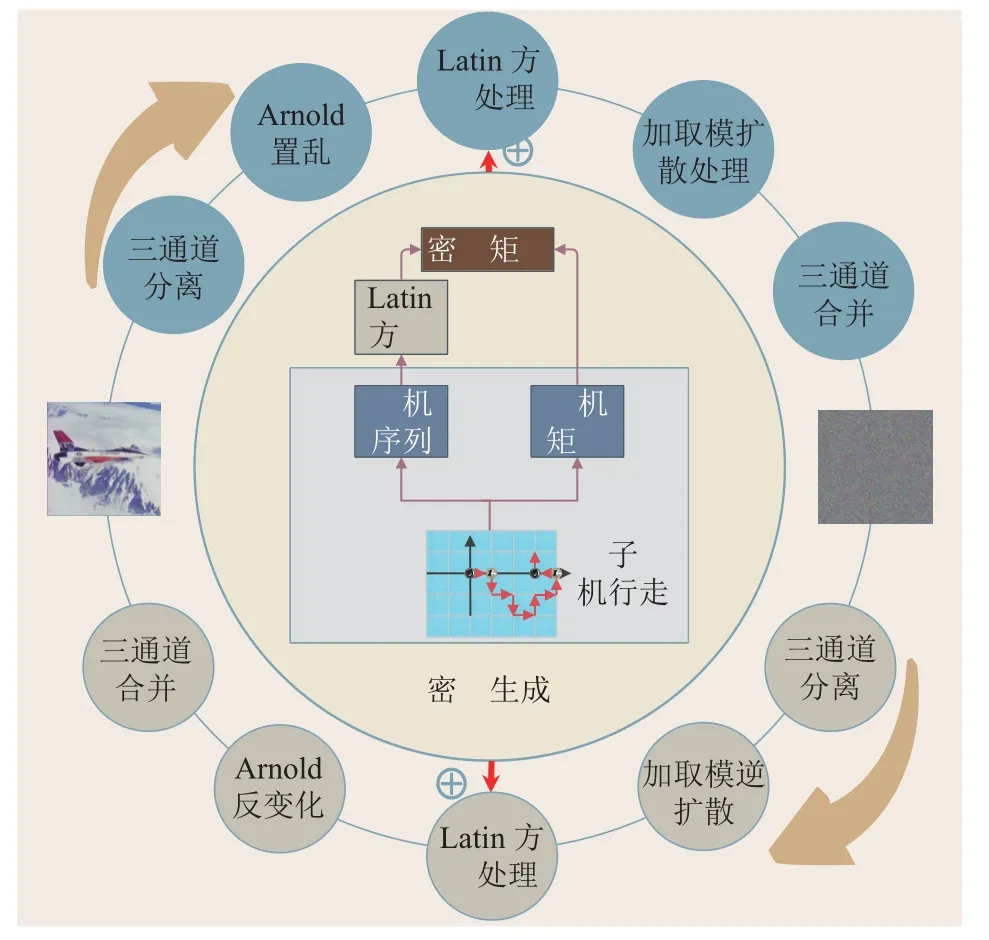
图4 算法流程图

2.1 加密步骤

1)输入待加密的大小为M×N的彩色图像I，将图像分别按行、列进行位置置乱得到初步置乱图像Io，然后把初步置乱图像Io分解成3 个单通道图像R1,G1,B1：

2)对分离后的3 个单通道图像R1,G1,B1分别进行Arnold 置乱，得到单通道像素点置乱图像R2,G2,B2。Arnold 置乱变换的公式如下：

3)通过离散量子漫步生成一个长度为512 的随机序列P1，然后把该随机序列平均分成两个长度为256 的随机序列P2和P3，并对两个随机序列利用文献[32]中的方法生成Latin 方阵LS：

4)利用量子漫步生成两个长度为M×N的随机序列P4和P5，通过如下的方法将随机序列的各个数据转化为大小在0～255 的序列S1和S2，然后把S1和S2转 化为大小为M×N的矩阵Q1和Q2：

5)利用Latin 方阵LS、Q1和Q2生成新的密钥矩阵Q3。 其中将LS作为 参 考 矩阵，Q1和Q2分别控制查找行、列：

6)将三通道图像R2,G2,B2分别与得到的密钥矩阵Q3按 位异或得到图像R3,G3,B3，即：

7)对图像R3,G3,B3进行加取模正向、逆向扩散处理得到单通道加密图像R4,G4,B4，加取模扩散算法的正向以及逆向公式为：

式中，Ci代 表R,G,B这3 个单通道加密图像；Pi代表R3,G3,B3；Si代 表随机序列；Di代表经过加取模扩散得到的单通道加密图像R4,G4,B4。

8)将3 个单通道加密图像合并得到最终加密彩色图像Ie。

2.2 解密步骤

1)将加密图像Ie的R,G,B三通道分离，得到3 个单通道加密图像R4,G4,B4：

2)对单通道加密图像R4,G4,B4进行加取模逆向、正向逆扩散处理得到图像R3,G3,B3。加取模扩散算法的正向以及逆向公式为：

3)将R3,G3,B3这3 幅单通道图像分别与加密阶段量子漫步产生的密钥矩阵Q3进行按位异或操作，得到图像R2,G2,B2：

4)对得到的R2,G2,B2这3 幅单通道图像分别进行Arnold 反变换，得到图像R1,G1,B1。Arnold 反变换公式如下：

5)将R1,G1,B1三通道图像合并，并对其进行行列置乱逆变换，得到解密图像。

3 实验结果及性能分析

为验证加密算法的可靠性与安全性，本文主要对Plane、Boat、Milk 和Lena 4 幅大小为512×512的彩色图像进行仿真实验以及结果分析。本文量子漫步选用参数(400, 801, π/3, π/2)。下面对图像的直方图、信息熵、相关性、抗攻击性、密钥空间及密钥敏感性多性能进行分析。

3.1 仿真结果

为证明该加密算法的可行性，本文对4 幅彩色图像进行了仿真实验，实验结果如图5 所示。由图5 可见，在加密后的图像上无法获得任何原图像的视觉信息，而解密后的效果与原图视觉感上是一致的。

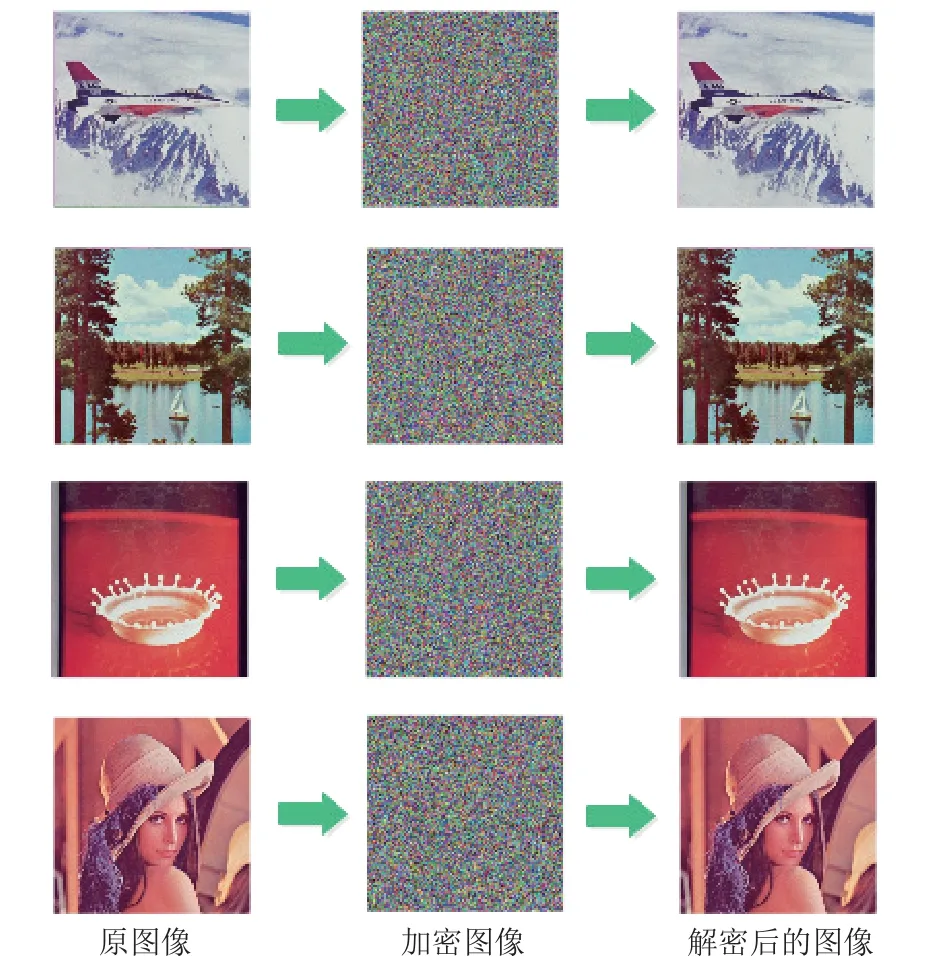
图5 加密和解密图像

3.2 直方图分析

直方图由一系列垂直的条纹组成，用以表示数据的分布情况：横轴为像素值，代表0～255 的色阶；纵轴表示图像中此像素值的像素点个数。本文对图像的原图及其加密图像的R,G,B三通道分别进行了直方图测试，测试结果如图6～图8 所示。

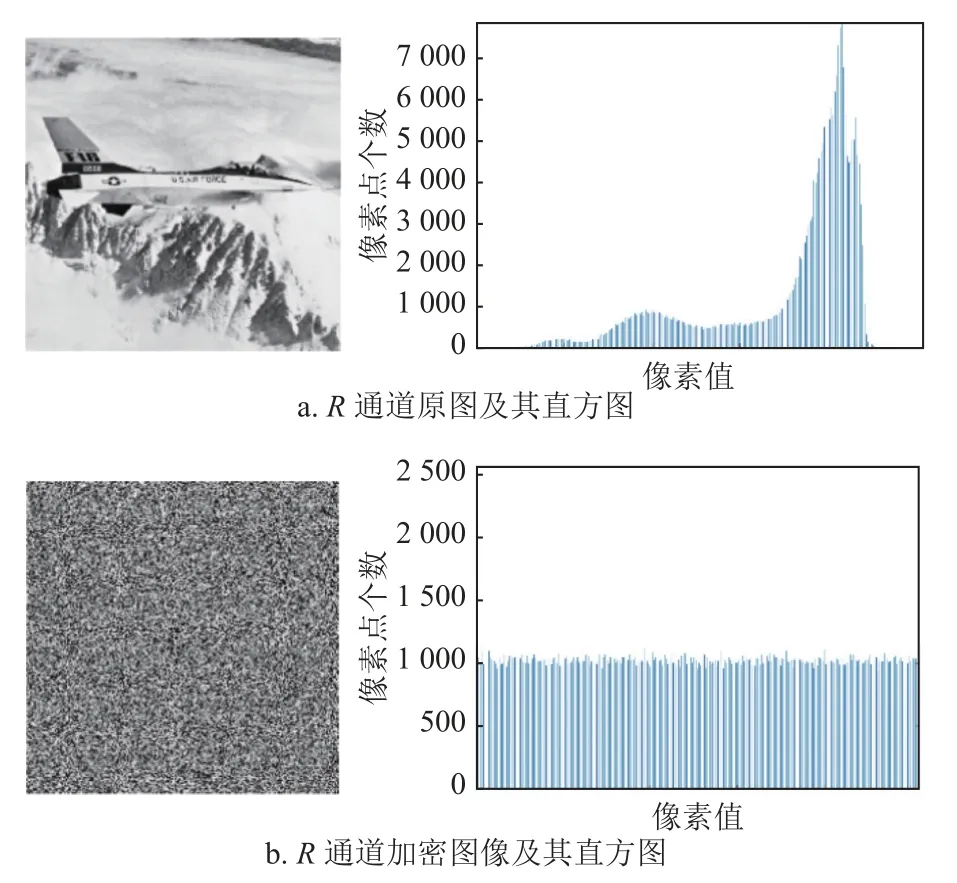
图6 R 通道原图、加密图像及其直方图

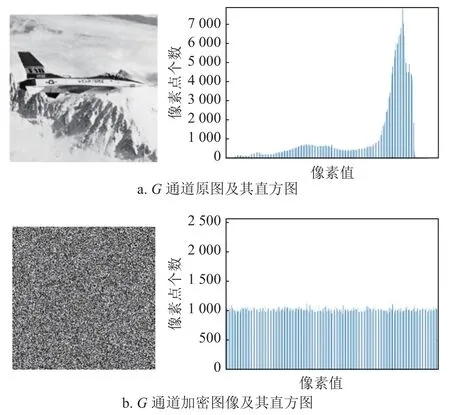
图7 G 通道原图、加密图像及其直方图

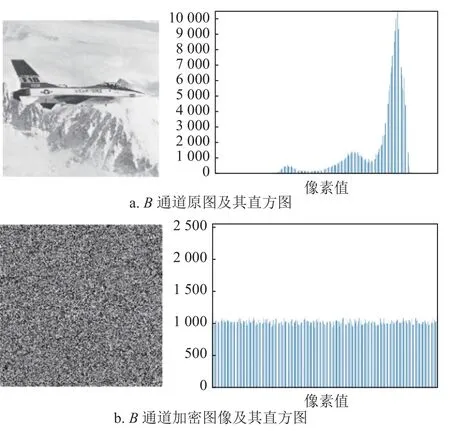
图8 B 通道原图、加密图像及其直方图

原图像的直方图像素分布不均，高低错落易于进行统计学分析，而加密后的图像像素分布均匀，无法据此进行统计学分析，具有良好的加密效果，能有效抵御统计学分析攻击。

3.3 信息熵分析

信息熵在描述图片像素点混乱程度上扮演着重要的角色。信息熵可以由以下公式计算得出：

式中，pi代表每个像素值出现的概率；N表示整幅图像像素点的数量总和。加密过程中像素值为[0,255]，加密图像信息熵值越接近8.0，说明图像的加密效果越好。本文测试了4 幅加密图像的熵值，信息熵值如表1 所示，并将加密的Lena 图像与文献[36]及文献[37]中的实验Lena 图像作了熵值对比。由本方案得到加密图像的信息熵值约在7.999 2 左右，接近于理想值8。因此，本文提出的加密算法具有良好的加密效果。

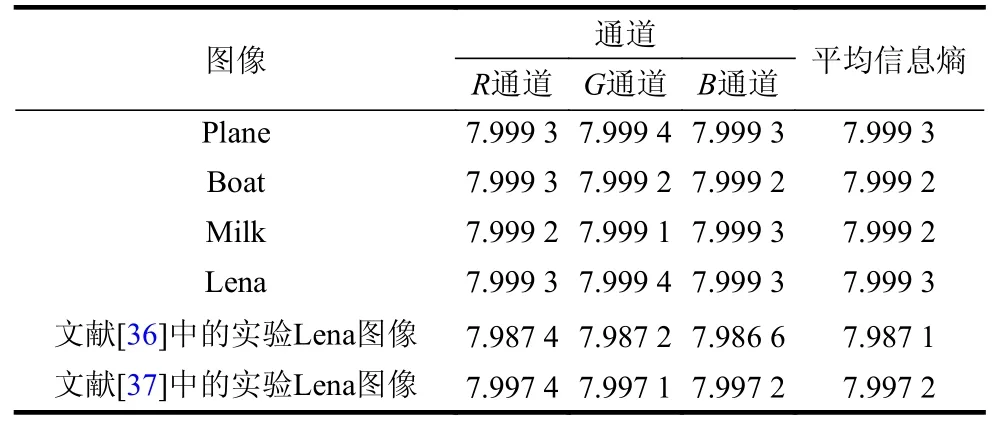
表1 加密图像信息熵

3.4 相关性分析

一副完整的图像中相邻像素之间具有很强的相关性，而加密效果好的算法往往能消除像素间的相关性。相邻像素的相关性主要体现在水平、垂直和对角方向上，且一般的彩色图像像素之间的相关性基本近似线性关系且相关系数趋近于1。对每一幅图像随机选择3 000 对像素值分别计算各方向的相关系数，计算相关系数的公式为：

式中， cov(x,y)表 示相邻像素点x和y之间的协方差；D(x)和D(y) 分 别表示像素点x和y的方差。本方案对Plane、Boat、Milk 3 幅彩色图像的加密图像进行了相关性分析，测试结果如表2 所示(视觉化效果如图9～图11 所示)。从相关性数值来看，各个方向的相关性均趋近于0，从图中看到加密前的图像相关性很强、呈线性关系，而加密后的图像像素之间的关系基本上不存在，像素无序分布，表明算法具有良好的加密效果。通过与其他方法比较，说明该加密算法有较好的加密效果。

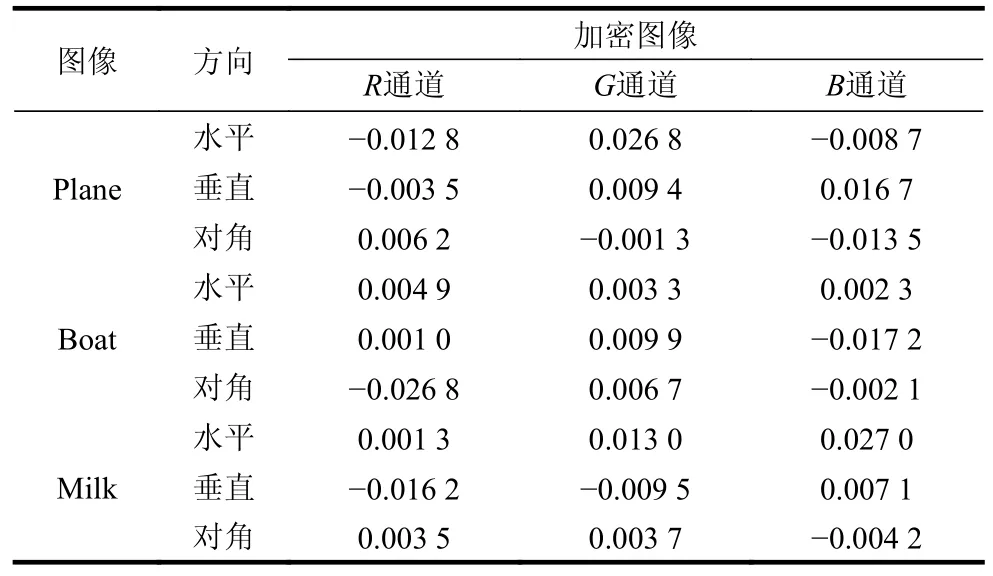
表2 像素相关性分析

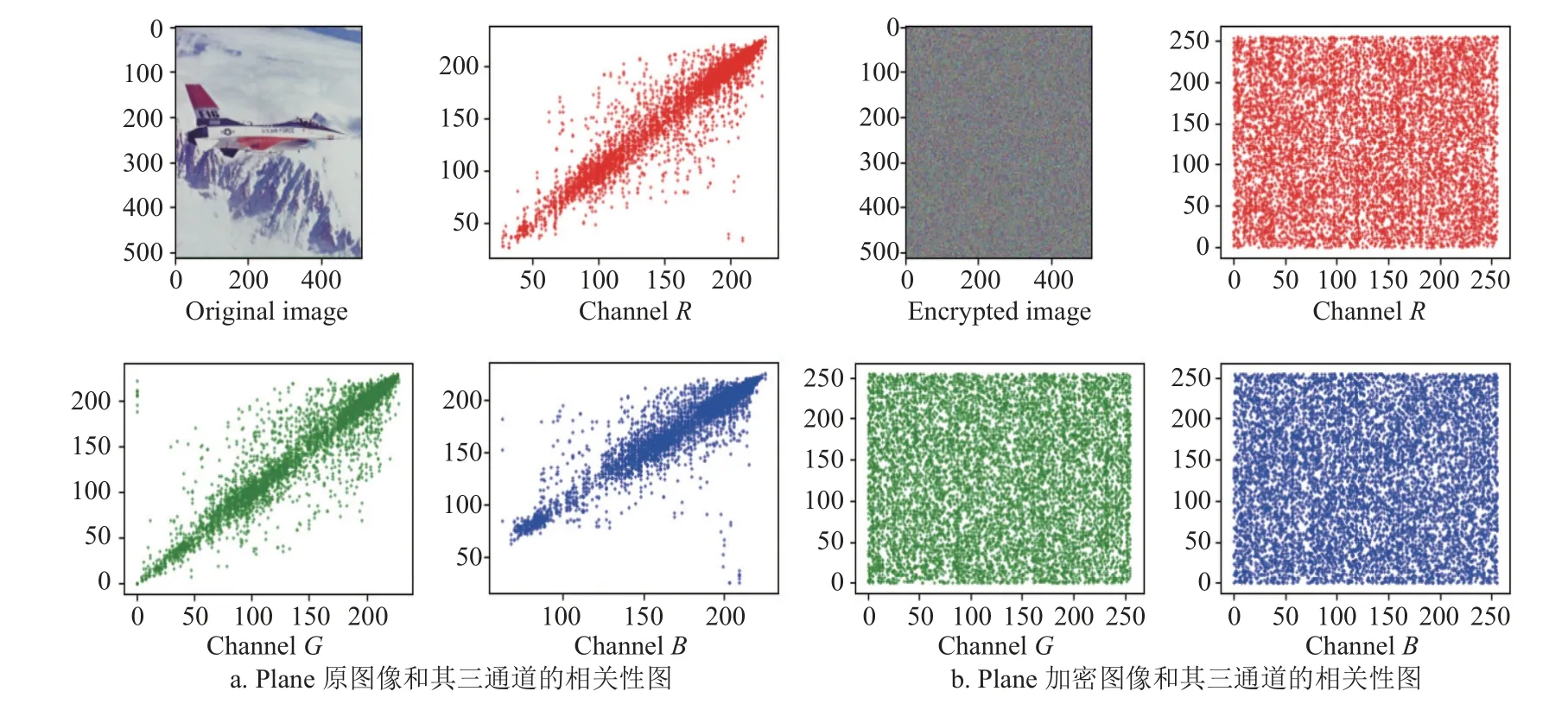
图9 图像Plane 和其对应的加密图像的三通道相关性图

3.5 抗噪声攻击性分析

在加密图像的数据传输过程中，可能会或多或少地掺入噪声，从而影响图像的解密。所以对于加密图像来说，抵抗噪声的能力是评价加密算法的一个重要指标。高斯噪声和椒盐噪声是最为常见的两类噪声，对加密图像Plane 分别加入强度为5%的椒盐噪声和均值为0、方差为0.000 5 的高斯噪声，图12和图13 分别为加密图像Plane 加入椒盐噪声和高斯噪声之后的图像以及其对应的解密后的图像。实验结果表明，该加密算法有着良好的抵抗噪声的能力。

图12 加入椒盐噪声的加密图像及对应的解密图像

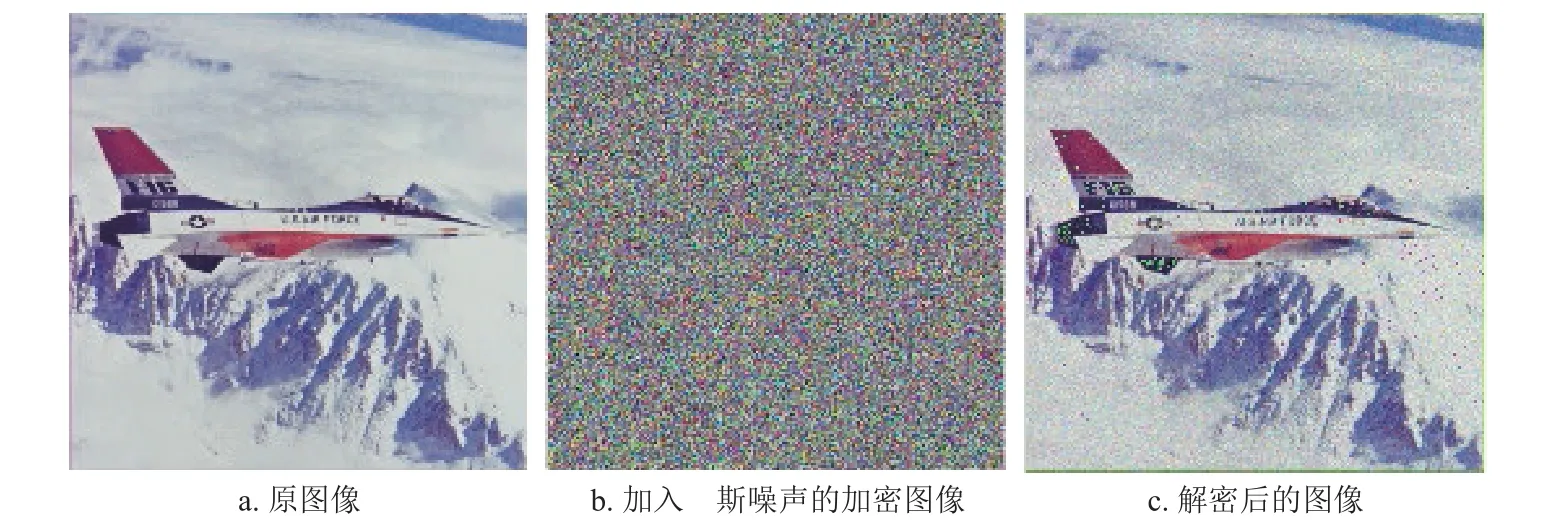
图13 加入高斯噪声的加密图像及对应的解密图像

3.6 抗裁剪攻击性分析

加密图像在网络传输中，可能会出现某一块区域的像素点丢失。因此，加密算法必须具有在加密图像缺损情况下解密的能力。如果在加密图像缺损情况下，原始信息在解密之后得以保留，说明该算法可以有效抵抗外界的裁剪攻击。对加密图像Plane移除一块 8 0×80像 素的红色通道、一块 50×80像素的绿色通道和一块 6 0×50像素的全通道，然后对其进行密，裁剪加密图像及其对应的解密之后的图像如图14 所示。实验结果表明，在加密图像的某一块区域的像素值缺失时，经过解密可以恢复原始图像信息，说明该加密算法具有良好的抵抗裁剪攻击的能力。

图14 裁剪之后的加密图像及对应的解密图像

3.7 密钥空间分析

一个优良的加密算法往往具有一个足够大的密钥空间。密钥空间越大，该算法抵抗外界暴力攻击的能力越强。在本加密算法中使用了交替量子漫步，交替量子漫步提供了无限的密钥空间。密钥空间在理论上达到2100时，加密图像就可以有效地抵抗暴力攻击。如果计算精度为1 0-15，那么该算法的密钥空间为1 060，这对保护加密图像的安全性已经足够了，因此该算法可以有效抵抗外部的暴力攻击。

3.8 密钥敏感性分析

差分攻击是破解加密图像的另一种常用手段。差分攻击是外界对原待加密图像的数据信息做微小的变动，然后利用加密算法对改变后的数字图像和原待加密图像分别进行加密，然后把两幅加密后的密文图像进行对比，找出原图像数据与加密图像数据之间的内在联系，利用二者之间的联系来进行破解加密图像。为了应对差分攻击，加密算法应该对密钥足够敏感。即当密钥发生一点变化，产生的加密结果应该是与原加密结果完全不同的。像素改变率(NPCR)和统一平均变化强度(UACI)是检验加密算法的密钥敏感性的两个重要指标，分别定义为：

式中，P1和P2分别代表密钥改变前后生成的两幅加密图 像。如果P1(i,j)=P2(i,j)，Q1(i,j)=0，反 之Q(i,j)=1，稍微改变随机行走的一个参数，产生其对应的加密图像，然后计算两幅加密图像的NPCR 和UACI，结果如表3 所示。并将Lena 图像的测试结果与文献[38]及文献[39]中的测试结果进行对比。测试结果表明，该加密算法具有良好的密钥敏感性。

表3 密钥敏感性分析 %

4 结 束 语

本文将Arnold 变换与Latin 方阵、量子漫步相结合，设计了一种新型的彩色图像加密方法。首先把彩色图像三通道分离，然后通过Arnold 变换对三幅单通道图像进行置乱处理。另一方面，利用量子漫步产生Latin 方阵和随机矩阵对初步置乱图像进一步处理，然后对处理之后的图像使用加取模扩散方法进行像素值的变换，最后把3 个单通道图像合并得到加密图像。经过实验仿真结果分析，加密图像的相关性非常低，信息熵接近于8，说明本文提出的算法具有比较良好的抵抗统计分析的能力；经过噪声攻击和裁剪攻击之后的加密图像在经过解密之后仍然可以看到原图像信息，说明本文提出的算法具有较强的鲁棒性；算法的密钥空间足够大且密钥敏感性良好，能够抵抗差分攻击。