珩磨缸套与活塞环表面弹塑性接触分析

汤义虎 ,林 缨 ,黄 立 ,李丽婷 ,孟祥慧

(1.上海交通大学 机械与动力工程学院,上海 200240;2.中国船舶集团有限公司第七一一研究所,上海 201108)

目前大多数船用发动机仍然采用内燃机，其中活塞环组-缸套是内燃机摩擦损失的主要来源，也是影响漏气量和滑油耗等整机动力性、经济性及可靠性指标的关键零部件.活塞环-缸套工作过程中与燃气直接接触，工作条件恶劣，在上止点处，活塞环缸套受高温高压燃气作用，常处于混合润滑甚至边界润滑状态，极易发生磨损失效.据统计，活塞环组缸套摩擦损失占内燃机总摩擦损失25%～50%[1]，活塞环组缸套故障占内燃机故障约34%[2].其中，拉缸是活塞环组缸套故障中最为典型的失效模式之一，已成为高指标内燃机开发的关键技术瓶颈[3].研究活塞环缸套表面接触压力、接触面积和应力等接触特性是了解表面接触状态、合理设计摩擦副以及预防拉缸等表面磨损失效的重要途径，对提升内燃机经济性和可靠性具有重要意义.

粗糙表面接触力学及数值计算方法的发展为研究粗糙表面接触特性奠定了基础.自从Greenwood等[4-5]建立弹性接触统计模型，考虑弹塑性变形[6-7]和非高斯分布表面[8]等因素的统计接触模型不断发展[9].另一方面，出于高精度接触分析的需要，近年来对基于确定性分析的粗糙接触数值模型也开展了大量研究.王文中等[10]采用快速傅里叶变换和共轭梯度法模拟了点接触单峰表面、正弦表面和粗糙表面的弹性接触.许迪初等[11]考虑微凸体接触弹塑性变形，通过数值计算分析了点接触实际接触面积、压力分布和微凸体塑性形变.刘检华等[12]通过数值仿真计算研究了弹塑性粗糙表面实际接触面积的影响因素，以及不同材料参数和表面形貌特征的粗糙表面接触行为.Liu等[13]，Urzică等[14]采用快速傅里叶变换(FFT)技术对粗糙表面的接触应力进行了分析.Sainsot等[15]对比了傅里叶变换和多重网格方法在接触分析中的应用.Zhang等[16]通过有限元计算方法，对比分析了粗糙表面接触统计模型与确定性模型的差异.针对缸套珩磨网纹这种服从双高斯分布、具有复合加工特征的纹理表面，Spencer等[17]使用均匀化技术生成具有规则形貌的珩磨网纹，并分析了其对缸套活塞环摩擦学性能的影响.Hu等[18]研究了缸套-活塞环表面接触及磨合过程中形貌的变化.Grabon等[19]通过活塞环和缸套摩擦试验，研究了载荷与缸套网纹表面形貌对其摩擦性能的影响.

虽然国内外对粗糙表面接触以及活塞环缸套摩擦学性能仿真开展了大量研究，但目前活塞环缸套摩擦学仿真[20-23]大多仍采用基于服从高斯或指数分布表面建立的GT(Greenwood &Tripp)统计接触模型[5]，针对缸套珩磨网纹这种具有复合加工特性、服从双高斯分布的表面，其真实接触模型及接触特性的研究仍不足，无法反映活塞环缸套摩擦副的真实表面接触状态，进而对后续的润滑与摩擦磨损分析产生影响.因此，本文中针对内燃机缸套珩磨网纹表面，基于边界元理论和半空间假设，建立缸套珩磨网纹表面无摩擦和法向弹塑性接触的确定性分析模型.本文中将采用快速傅里叶变换(FFT)和共轭梯度法，对缸套珩磨网纹表面与活塞环接触特性进行数值模拟分析，获得表面接触特性，并研究不同载荷条件下的接触面积及应力的演变规律.

1 珩磨缸套与活塞环弹塑性接触模型

1.1 粗糙面接触变形

考虑到活塞环硬度远大于缸套，为了研究珩磨缸套与活塞环的接触特性，本文中采用理想弹塑性缸套珩磨网纹表面和刚性活塞环平面(图1)，对法向受压无摩擦作用下的接触模型进行了研究.

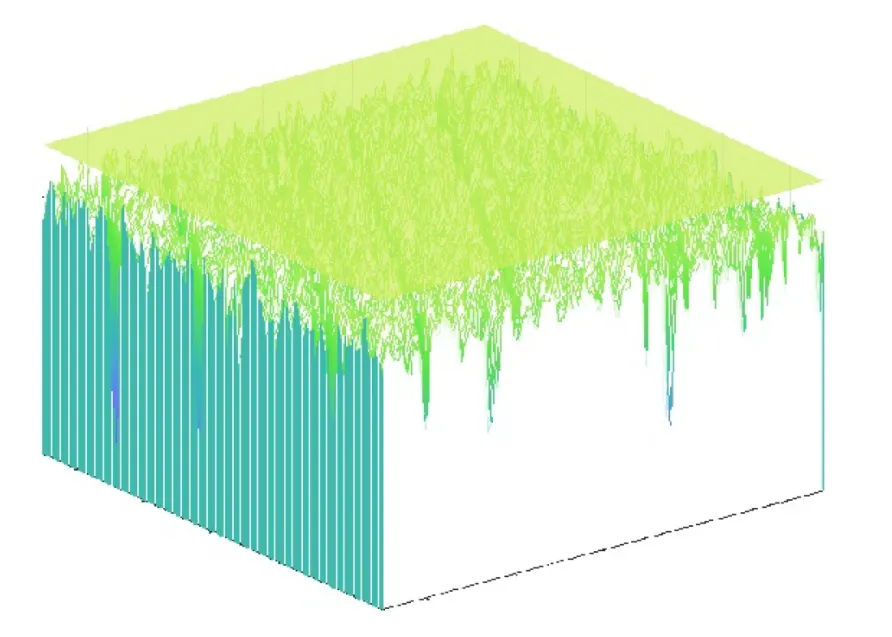
Fig.1 Contact model between the honed liner and the rigid plane图1 缸套珩磨网纹表面与刚性平面接触模型

根据几何约束条件，两表面接触间隙h满足以下关系：

其中，g为初始间隙，u为法向变形，δ为刚体位移.法向变形u包含弹性变形ue和塑性变形up.根据边界元理论，对于受表面分布压力p作用的均匀半空间，在表面点(x,y)处的法向弹性变形ue可以由Boussinesq积分表示为

其中，ξ1和ξ2为压力作用点的x和y坐标，p(ξ1,ξ2)为(ξ1,ξ2)点处作用的压力，G为格林函数，E*为综合弹性模量，由式 1/E*=(1-ν1)/E1+(1-ν2)/E2确定，E1、E2和ν1、ν2分别为相互接触表面的弹性模量和泊松比.

上述法向弹性变形的离散形式可以表示为

其中，D是法向变形的影响系数，其可通过格林函数G不定积分求得解析解.i、j和M、N分别为x、y方向的离散网格节点编号和节点数.

在接触区和非接触区内，表面接触间隙和接触压力需满足以下约束条件：

上述方程所描述的接触问题即为线性互补问题，其中，Ωc为接触区，H为软材料的硬度.相较于弹性接触模型，当接触压力超过软材料硬度时，理想弹塑性模型对接触压力进行截断修正[24].另外，根据变分原理，上述方程等价于求解最小势函数的条件极值问题.

其中，V为系统的总势能，右边第1项为内能，后2项为外力功，其中w为作用在表面的外载荷，pT为p的转置.K为由公式(4)确定的影响系数矩阵.

1.2 粗糙面接触应力

对于受表面法向分布压力p作用的均匀半空间，点(x,y,z) 处的接触应力σ可由下式表示：

将上述接触应力进行离散化，其离散形式可以写为

与弹性变形求解相似，上式中，Ds是法向载荷作用的应力影响系数，其可通过格林函数Gs不定积分求得解析解，i、j、k和M、N、L分别为x、y、z方向的离散网格节点编号和节点数.关于应力影响系数的求解详见文献[13].

2 粗糙面接触数值分析方法

通过变分原理将接触问题转化为式(6)所描述的极值问题后，就可以应用共轭梯度法和二次规划等方法求解.在数值求解中，主要的工作量集中在弹性变形及应力的计算上.理论上，由法向载荷作用的变形以及应力影响系数可求得解析解，即式(4)和式(8)的系数矩阵已知，通过线性变换可以计算给定接触压力情况下的接触变形和应力，但存在(MN)2复杂度的大型矩阵运算问题[25].由式(4)和式(8)可见，法向载荷引起的变形和应力为离散卷积形式，可通过离散傅里叶变换及其逆变换获得相应接触变形和接触应力[26-27]，其复杂度为MNlog2(MN)，从而节省计算资源和时间.

本文中采用Polonsky等[28]描述的共轭梯度法迭代求解接触压力.接触变形及接触应力的求解采用FFT技术，计算方法简单叙述如下：

(1) 在计算区域内，根据输入载荷初始化接触压力p；

(2) 根据公式(4)，利用FFT计算接触表面的弹性变形ue；

(3) 计算梯度方向和步长，并据此更新接触压力p；

(4) 根据硬度H调整接触压力，并根据几何约束关系计算塑性变形up[24].

(5) 根据载荷平衡，修正接触压力p；

(6) 检查压力迭代精度，重复公式(2～4)，直至满足精度要求；

(7) 最后由公式(8)根据接触压力利用FFT计算应力.

3 缸套珩磨网纹表面与活塞环接触分析结果与讨论

在接触分析中，缸套珩磨网纹表面可以采用三维实测表面或仿真模拟表面作为输入，本文中采用仿真模拟生成的缸套珩磨表面(沟槽粗糙纹理的粗糙度Rpq=0.35 μm，平台部分精细纹理的粗糙度Rvq=1.98 μm，沟槽与平台交点处的支承率Rmq=84%)作为输入，如图2所示(s表示标准偏差).在X，Y和Z方向上0.5 mm ×0.5 mm × 1 mm的计算区域内，采用256 × 256 × 256的网格离散.缸套表面弹性模量为150 MPa，泊松比为0.3，硬度为800 MPa.活塞环表面弹性模量为210 MPa，泊松比为0.3，硬度为8 000 MPa.活塞环表面粗糙度Rz值为4 μm，表面硬度远超过缸套表面，因此，本文中在接触模型开始处所述将活塞环假定为刚性平面.

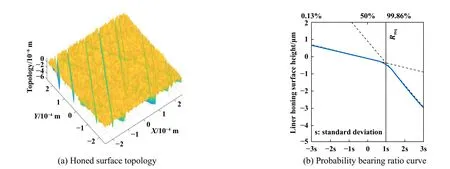
Fig.2 Honed surface topology and material probability curve(Rpq=0.35 μm,Rvq=1.98 μm,Rmq=84%)图2 珩磨网纹表面形貌及概率支承率曲线(Rpq=0.35 μm,Rvq=1.98 μm,Rmq=84%)

基于上述弹塑性接触模型及数值方法，仿真分析了缸套珩磨网纹表面在法向载荷为100 N作用下接触压力、弹塑性接触变形及接触应力.

由图3所示的接触压力可以看出，缸套珩磨网纹表面载荷由平台部分接触承载，珩磨波谷表面无接触，接触区各微凸体接触承载较均匀，接触压力达到800 MPa.但观察接触变形结果(图4)可以发现，由于受珩磨网纹粗糙轮廓影响，接触区弹性变形及塑性变形并不均匀，在非接触区的深波谷附近，弹性变形较小.缸套珩磨网纹表面弹性变形最小值为2.2 μm，最大值为2.46 μm，塑性变形最小值为0，最大值为1.3 μm.

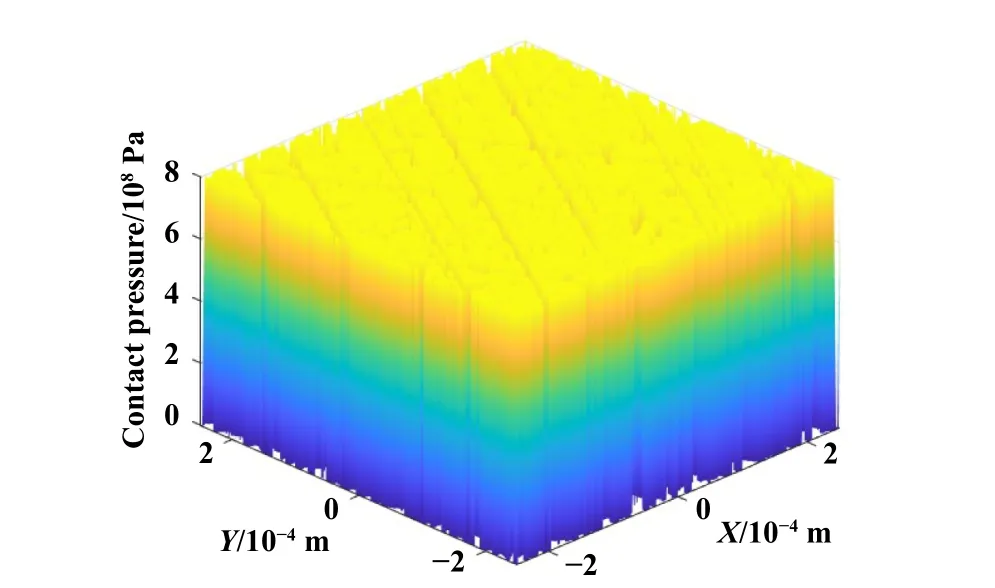
Fig.3 Contact pressure on honed surface under a nominal load of 100 N图3 缸套珩磨网纹表面在法向载荷为100 N作用下接触压力

Fig.4 Contact deformation on honed surface under a nominal load of 100 N图4 缸套珩磨网纹表面在法向载荷为100 N作用下的接触变形

图5(a)所示为X=0截面上缸套珩磨网纹轮廓及弹塑性变形，可以发现，在Y=-0.2、-0.1和0.15 mm等珩磨网纹平台轮廓附近，虽然存在一定弹性变形量，但塑性变形较小，表明该区域微凸体刚开始进入接触.在网纹轮廓波谷处等非接触区，受其余接触点对非接触区的变形叠加影响，非接触区的弹性变形不为0，而塑性变形为0.受缸套珩磨网纹粗糙轮廓高度分布影响，在粗糙峰接触处，弹性变形较大，同时存在较大的塑性变形.图5(b)所示为变形后轮廓高度及接触压力，可以看出，在载荷作用下，微凸体被压平.

Fig.5 Elastoplastic deformation,profile height and contact pressure at X=0 on honed surface under a nominal load of 100 N图5 100 N法向载荷作用下，缸套珩磨网纹表面X=0弹塑性变形、轮廓高度及接触压力

为了分析缸套网纹表面的应力状态，分别截取X=0垂直面，以及Z=-7.8 μm和-0.5 mm平面进行应力分析，结果如图6和图7所示.根据图6(a)接触应力三维图可以看出，应力在Z方向上总体呈先增大后减小的趋势，但在靠近接触表面，应力状态复杂.如图6(b)所示，在0.01 mm附近表面层应力达到最大，且高于材料内部次表面层最大应力.对比图6与图5可知，表面层应力较大区域与弹塑性变形区域相对应，在弹塑性变形较大处，对应应力也较高.

Fig.6 Von-Mises stress distribution in vertical at honed surface X=0 under a nominal load of 100 N图6 100 N法向载荷作用下，缸套珩磨网纹表面X=0垂直方向Von-Mises应力分布

Fig.7 Von-mises stress distribution in horizon on honed surface under a nominal load of 100 N图7 100 N法向载荷作用下，缸套珩磨网纹表面水平方向Von-mises接触应力分布

对比水平面应力分布，可以发现相同趋势.由图7(a)与图4可见，水平面应力分布与接触变形对应，在变形较大处，对应应力也较高.对比图7所示的Z方向不同深度下的应力分布可见，在靠近表面应力状态受表面接触压力及变形影响较大，而随着Z方向深度的增加，应力分布受表面载荷影响减小，应力分布更加均匀，符合圣维南原理.

不同载荷下缸套珩磨表面接触压力演变如图8所示.从图8中可以看出，随着载荷增加，表面接触压力为0的面积逐渐减小，载荷作用面积不断增大.载荷和接触面积的定量关系如图9所示.在100 N载荷作用下，珩磨网纹表面接触面积高达50%，随着载荷增加，接触面积线性增加，在150 N时，珩磨网纹表面接触面积高达75%，接触载荷与接触面积几乎呈线性关系.

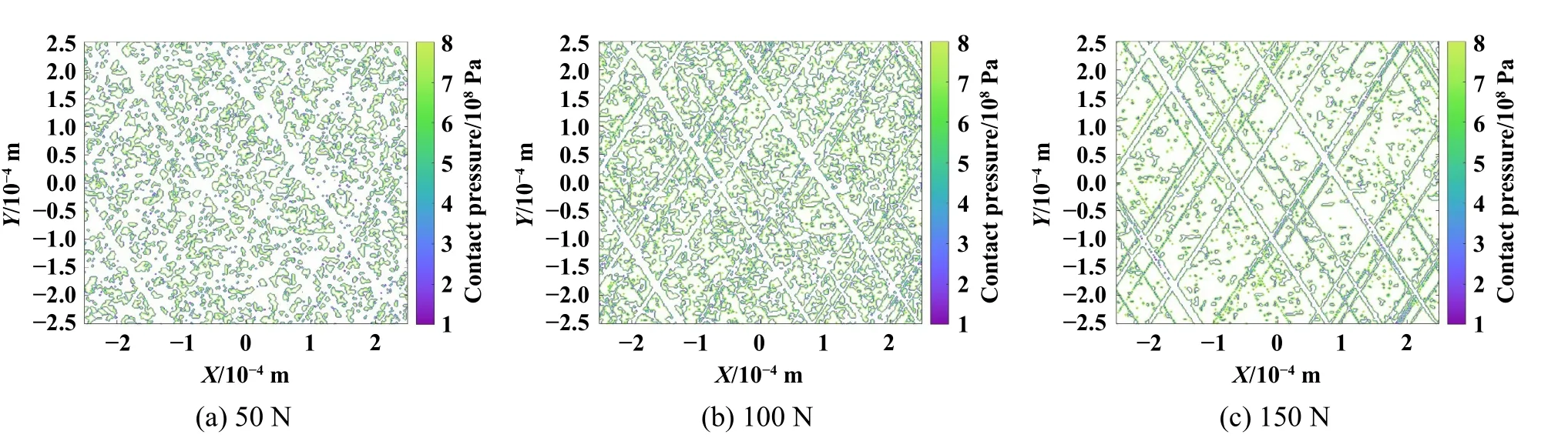
Fig.8 Evolution of contact pressure on honed surface under different load图8 缸套珩磨网纹表面不同载荷下接触压力演变

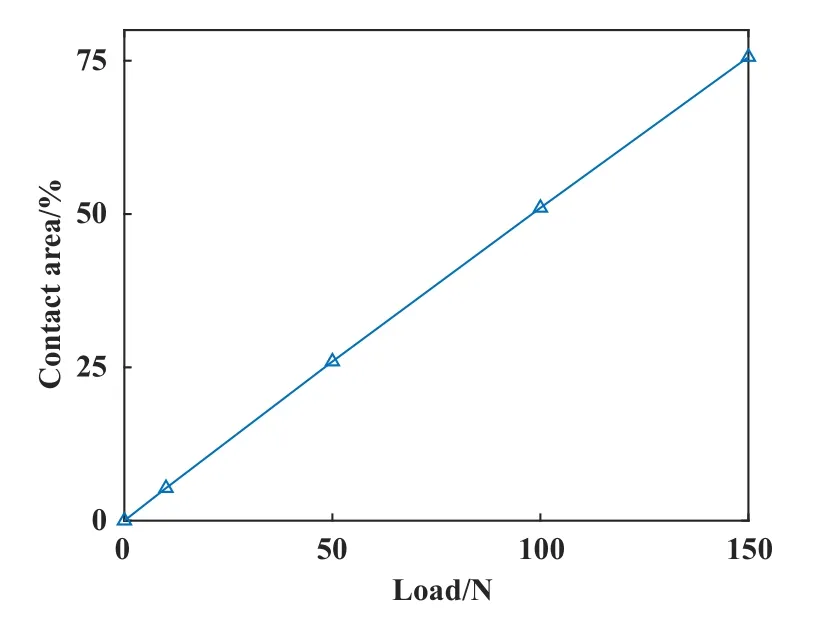
Fig.9 Relation between contact area and load on honed surface图9 缸套珩磨网纹表面载荷-接触面积关系

图10所示为缸套珩磨网纹表面X=0处不同载荷下应力演变结果图，从图10中可以看出，在较低载荷50 N作用下，近表面层应力大于材料内部次表面层应力；随着载荷增加，近表面层应力逐渐减小而材料内部次表面层应力增加；当载荷增大至150 N时，材料内部次表层应力大于近表面层应力.发生该现象的原因可能为，在增大载荷作用下，接触粗糙峰数量和接触面积逐渐增大，原先由孤立的微凸体承载引起的集中应力，逐步演化为由更多微凸体承载并逐步接近表观面积，从而降低了粗糙峰对近表面层集中应力的影响.

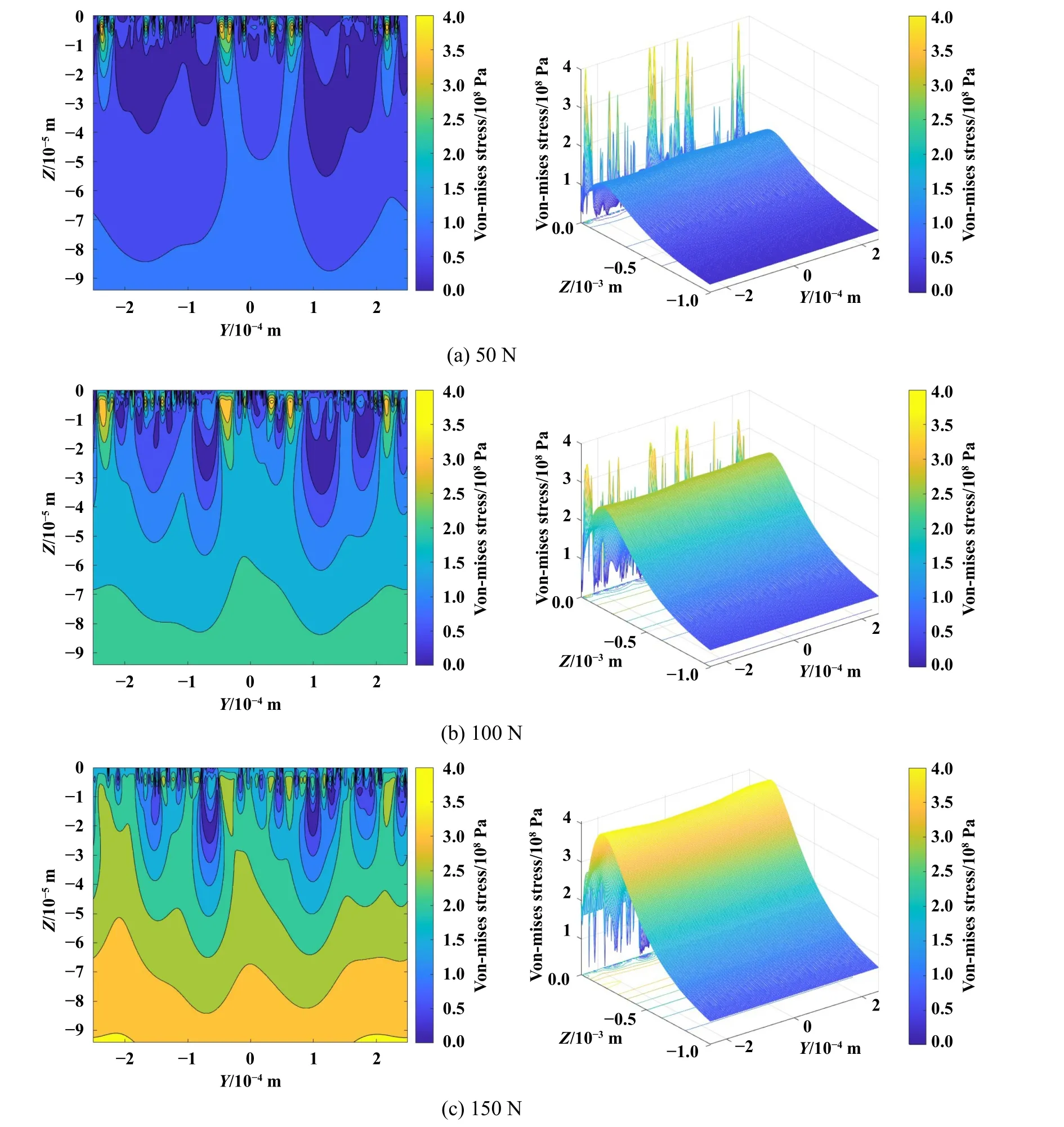
Fig.10 Evolution of stress on honed surface at X=0 under different load图10 不同载荷下，缸套珩磨网纹表面X=0处应力演变

4 结论

本文中基于边界元理论，在假设活塞环表面为刚性平面情况下，建立了缸套珩磨网纹表面与活塞环弹塑性接触力学模型；通过快速傅里叶变换以及共轭梯度法，实现了缸套网纹表面接触模型的数值仿真分析，获得了接触压力及接触面积、表面弹性变形和塑性变形以及应力分布等接触特性参数，并分析讨论了载荷与接触压力、接触面积及应力的关系和演变规律，得出如下结论：

a.考虑弹塑性接触模型，缸套网纹表面接触压力较均匀，说明作用载荷由各微凸体均匀承载；

b.在波谷等非接触区，受变形叠加影响，非接触区弹性变形不为0，而塑性变形为0；

c.缸套珩磨网纹表面作用载荷与接触面积呈线性关系，随着载荷增大，接触面积线性增加；

d.低载荷作用下，近表面应力大于材料内部次表面应力；随着载荷增加，次表面应力增大，而近表面应力降低；高载荷作用下，表面接触接近表观接触面积，次表面应力超过近表面应力.

本文中建立的弹塑性接触模型为基于理想塑性条件下的分析，未考虑材料塑性流动和应变硬化等影响因素.此外，针对活塞环缸套实际工作环境，需进一步考虑摩擦切向加载和温度等影响.以上方面仍待后续进一步探索研究.