管道封堵机器人的大变形橡胶筒静态密封特性仿真与试验研究
2023-10-13李泽良
唐 洋 ,王 远 ,李泽良 ,孙 鹏 ,刘 祥 ,王 强 ,吴 聚
(1.西南石油大学 机电工程学院,四川 成都 610500;2.西南石油大学 能源装备研究院,四川 成都 610500;3.四川航天烽火伺服控制技术有限公司,四川 成都 610500)
大变形橡胶筒是管道封堵机器人最为重要的核心组成部件之一,其作用主要是密封管道、隔绝管道内油气以及保护管道.现场使用中,橡胶筒密封失效和撕裂失效问题较为突出,已成为当前关注的焦点问题之一[1-4].
为了揭示大变形橡胶筒密封和损伤失效机理,国内外学者对封隔器胶筒做了相关研究.Hu等[5]通过数值模拟和试验对比,对压缩式封隔器填料元件密封性能进行了研究.Dong等[6]研究了压力作用下,应力松弛对织物橡胶密封性能的影响.张智等[7]采用正交优化方法,对橡胶筒的长度、厚度和倒角尺寸进行了优化,获得了橡胶筒结构参数的优化组合方案.王晓龙等[8]分析了在20 MPa载荷下,橡胶筒与套管和中心管间的接触应力分布规律、橡胶筒Mises应力变化规律和剪切应力变化规律.张康等[9]通过仿真研究了橡胶筒的自密封特性,分析了不同橡胶筒硬度对其自密封性能的影响.黎伟等[10]分析了不同摩擦系数、橡胶筒厚度、工作压力和环空间隙等因素对橡胶筒变形的影响.上述研究主要涉及封隔器中橡胶力学性能分析,也有涉及其结构改进部分.类似橡胶筒在封隔器上使用较多,并且其为常规的小变形的橡胶筒.然而,管道封堵机器人橡胶筒与封隔器橡胶筒有明显区别,需考虑橡胶材料特性、几何形状、管内高压和大尺寸等因素.
因此,在本研究中选取5种不同类型的橡胶材料作为试验对象,拟合出5种橡胶材料的本构模型;其次采用有限元方法研究橡胶材料和橡胶筒几何参数对管道封堵机器人密封特性的影响;进一步采用多因素分析方法对橡胶筒结构参数进行优化,从而提高橡胶筒的密封性能和使用寿命.本研究的结果对开发高性能、高寿命以及高可靠性管道封堵机器人具有重要的参考意义.
1 管道封堵机器人橡胶筒多阶段变形力学分析
管道封堵机器人封堵模块由支撑轮、施力块Ⅰ、橡胶筒、施力块Ⅱ、卡瓦和支撑盘组成,如图1所示.橡胶筒承受轴向载荷,会发生形变膨胀贴合管壁,与管壁产生接触应力.接触应力随着橡胶筒膨胀而增大,最终将管壁与机器人间的环形通道封住[11].
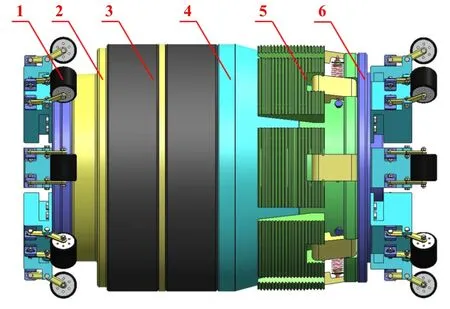
Fig.1 Structure model of pipeline plugging robot sealing module: 1.support wheel;2.pressing block I;3.rubber cylinder;4.pressing block II;5.slips;6.support plate图1 管道封堵机器人封堵模块结构模型图:1.支撑轮;2.施压块Ⅰ;3.橡胶筒;4.施压块Ⅱ;5.卡瓦;6.支撑盘
橡胶筒受轴向力产生的变形可分为自由变形和约束变形2个阶段[12].橡胶筒密封管道所需的总挤压力F为
其中,Fε为橡胶筒自由变形阶段所需的压力;FΔP为橡胶筒约束变形阶段所需压力.
1.1 橡胶筒自由变形阶段力学分析
当管道封堵机器人橡胶筒受到轴向载荷时,从初始状态到接触管壁前的过程称为自由变形阶段.假设完全符合胡克定律,在自由变形阶段中橡胶筒的应力应变呈线性关系.此时,橡胶筒内任一质点的径向位移微分方程[13]为
其中,u为橡胶筒的径向位移(单位mm);r为曲率半径(单位mm).
通解为
由边界条件得
将式(4)和(5)代入式(3)得
其中,R1为橡胶筒内半径,R1=169 mm;R2为橡胶筒外半径,R2=186 mm;R3为管道内半径,R3=196 mm.
橡胶筒相对径向应变为
橡胶筒相对切向应变为
假设橡胶筒的体积变化为
其中,εz为橡胶筒相对轴向应变.
由于橡胶圈的材料为丁腈橡胶,是1种塑性低、硬度极高的材料[14].在承受压力时具有不可压缩性,因此体积变化为
其中,V为橡胶筒体积;L为橡胶筒长度.
可知橡胶筒相对轴向应变为
由广义胡克定律可以求得橡胶筒承变形时的径向应力、切向应力和轴向应力:
其中,负号“-”表示轴向应力为压应力.
得出橡胶筒在自由变形阶段所承受的轴向力
其中,E为橡胶筒弹性模数,E=7.84 MPa;μ为泊松比,μ=0.5.
由于(R3-R2)是在初始状态下橡胶筒与管道内壁之间的间隙值.因此,管道内壁与橡胶筒之间的环向间隙越大,压缩橡胶筒与管道内壁接触所需的轴向挤压力也越大.
1.2 橡胶筒约束变形阶段力学分析
所设计的管道封堵机器人要求密封10 MPa油气介质.即10 MPa的压差作用在橡胶筒一侧的环形截面上时,管道封堵机器人仍能够有效封堵油气管道.根据管道轴向上的力学平衡条件可知,压差 ΔP作用在橡胶筒上的推力与橡胶筒和管壁间的摩擦力相等[15],即
其中,Sh为橡胶筒外径与管道内径间的环形面积;So为橡胶筒变形后与管道接触形成的外密封面积;f为橡胶筒与管壁间的摩擦因数,取极限值0.3;P1为理论接触应力,L为橡胶筒长度,L=180 mm;ΔL为橡胶筒长度差.
轴向压缩应变量 εz:
橡胶筒在密封工作状态下所需的轴向压缩力:
保证橡胶筒能够密封管道所需要的总压力:
管内压差作用在橡胶筒环形面上的作用力以及接触应力与纵向变形量之间的关系:
其中,F1为橡胶筒所受的轴向挤压力;A0为橡胶筒侧面环形面积;A1为橡胶筒变形后与管道间侧面环形面积;σj为沿橡胶筒截面的平均轴向应力;η为纵向变形量;ρ0为橡胶筒内外径之比;Pk为接触应力;G为抗剪切弹性模量,G=2.65 MPa;ω为与橡胶筒内外径有关的调节系数[16].
计算得出,当出现接触应力Pk大于等于7.26 MPa时,可认为管道封堵机器人能够有效封堵住10 MPa压力的介质.
管道封堵机器人中橡胶筒的密封性能不仅与橡胶筒和管道之间的接触应力有关,还与橡胶筒和管道之间的有效接触长度有关.考虑到这一点,有学者应用密封性能系数K来评价弹性密封材料的密封性能[17].密封性能系数K等于橡胶筒和管道之间的平均接触应力和有效接触长度的乘积.
其中,Pk为平均接触应力,Lk为有效接触长度.
橡胶筒在未损坏的情况下,密封性能系数K值越大,橡胶筒的密封性能越好.
2 橡胶材料试验与本构模型分析
橡胶材料作为1种高度非线性的复合材料,因其本构关系复杂,无法简单通过固定的材料参数来描述其力学性能,所以前人在大量试验数据基础上建立了理论模型,并确定了一系列本构模型常系数[18-20].
2.1 橡胶常用本构模型
2.1.1 Arruda-Boyce模型[21]
Arruda-Boyce模型适用于模拟橡胶3倍的应变,在大应变硬化的情况下同样适用.其应变能函数表达式为
其 中,C1=1/2,C2=1/20,C3=11/1050,C4=19/7050,C5=519/673750,Ci为材料剪切性能参数,u为初始切变模量,λm为自锁应变,为应变不变量,D为材料压缩性能参数,J为弹性体积比.
2.1.2 Van Der Waals模型[22-23]
Van Der Waals模型与Arruda-Boyce模型相比具有更好的拟合性能,在预测橡胶变形能力上较优.其应变能函数表达式为
2.1.3 Mooney-Rivlin模型[24]
Mooney-Rivlin模型是多项式模型中最简单的模型.其应变能函数表达式为
其中:C10和C01均为材料剪切性能参数,D1为材料压缩性能参数.当材料的精确参数不确定时,通常采用Mooney-Rivlin模型.该模型适用于小应变或中应变(100%拉伸应变,30%压缩应变).
2.1.4 Yeoh模型[25]
Yeoh模型在大应变情况下应变能与试验结果吻合情况较好.其应变能函数为
其中,N为函数的阶数,N越大,拟合精度越高.
2.1.5 Ogden模型[26]
Ogden模型一般适用得应变范围较大(达700%),应变能函数为
2.2 橡胶的单轴拉伸压缩试验
不同材料的橡胶,仿真分析时本构模型不同,需进行材料拉伸压缩试验,得出应力与应变之间的关系,拟合出合适的本构模型.单轴拉伸试验按照GB/T 528-2009的方法,单轴压缩试验按照GB/T7757-2009的方法,具体试验方式如下.
选取邵氏硬度为70 HA、75 HA、80 HA、85 HA和90 HA的丁腈橡胶作为试验材料.拉伸试样采用Ⅰ型哑铃状试样,总长为115 mm,端部宽25 mm,试件中部宽6 mm,厚2 mm.压缩试样采用圆柱体,直径为29.0±0.5 mm,高度为12.5 ±0.5 mm.
橡胶拉伸压缩试验数据处理后得到的不同邵氏硬度试样应力应变曲线,如图2所示.

Fig.2 Uniaxial tensile and compressive stress-strain curves of rubber at different hardness图2 不同硬度下橡胶单轴拉伸压缩应力-应变曲线
从图2中可以看出,随着橡胶硬度增加,压缩或拉伸相同应变所需的应力增大.在有限元仿真软件中利用最小二乘法对单轴拉伸和压缩试验的应力-应变数据进行拟合[27-28].优选出最适合不同硬度橡胶力学性能的本构模型并列于表1中.

表1 不同材料橡胶的拟合本构模型Table 1 Fitting constitutive models of rubber with different materials
3 橡胶筒的密封特性研究与结构优化
所设置的分析变量为橡胶筒的硬度、轴向长度L、径向厚度b以及受压边的倾斜角 α.橡胶筒截面示意图如图3所示.
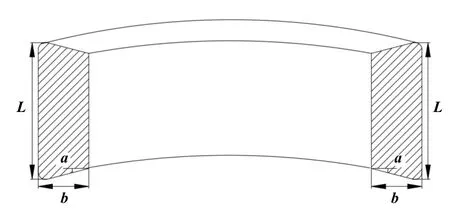
Fig.3 Schematic diagram of cross-section of the rubber cylinder图3 橡胶筒截面示意图
3.1 橡胶筒在不同材料硬度下的密封性能分析
将硬度为70 HA、75 HA、80 HA、85 HA和90 HA的橡胶材料根据上述选择的本构模型进行设置.设置载荷为523.56 kN,5种硬度橡胶筒与管壁的接触应力分布曲线如图4所示,橡胶筒的肩部应变如图5所示,橡胶筒与管道接触参数列于表2中.

表2 不同硬度橡胶筒与管道接触参数表Table 2 Contact parameters between rubber cylinder and pipe with different hardness
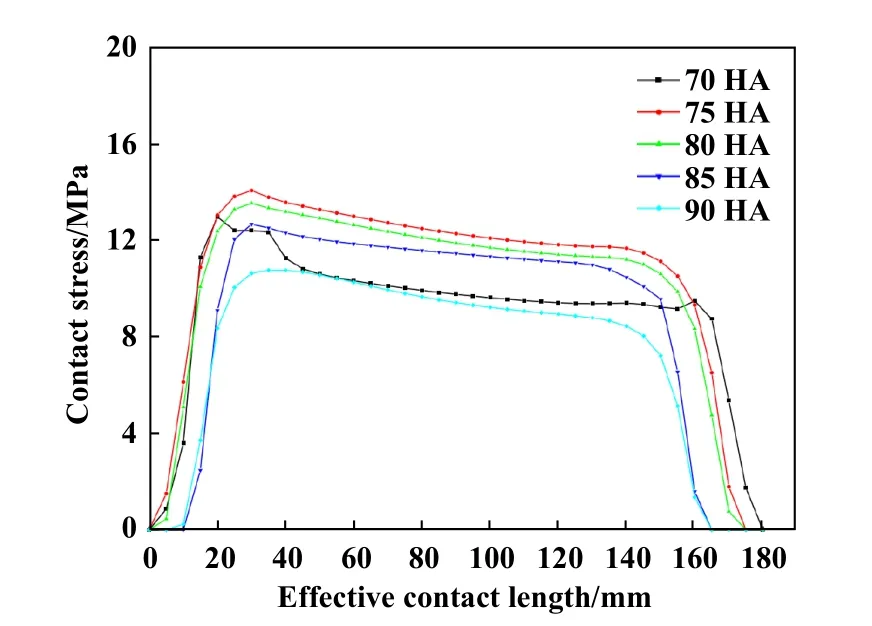
Fig.4 Contact stress distribution curve between rubber cylinder and pipe wall with different hardness图4 不同硬度橡胶筒与管壁接触应力分布曲线

Fig.5 Strain cloud diagram of rubber cylinder with different hardness图5 不同硬度橡胶筒肩部应变云图
通过对上述不同硬度橡胶筒与管壁接触应力分布结果、橡胶筒与管道接触参数和不同硬度橡胶筒肩部应变云图进行分析可知:
(1) 橡胶筒硬度为75 HA时,接触应力最大可达到14 MPa,密封性能系数K为1 721,密封效果较好,但橡胶筒的应变较大,最大值为140.7%.
(2) 随着橡胶筒硬度的增加,橡胶筒与管道之间的接触应力先增大后减小.在硬度为75 HA时,橡胶筒与管道间的接触应力最大.在硬度为85 HA时,橡胶筒应变最小为47.48%.
(3) 70 HA、75 HA和80 HA硬度的橡胶筒有明显的肩凸现象,会缩短橡胶筒的使用寿命.
为进一步优选出满足密封条件的橡胶筒材料,根据橡胶筒硬度设置不同载荷,保证密封效果相近(最大接触应力近似相等),参数列于表3中,分析橡胶筒的形变损伤,如图6所示.

表3 不同硬度橡胶筒载荷与最大接触应力Table 3 Load and maximum contact stress of rubber cylinders with different hardness
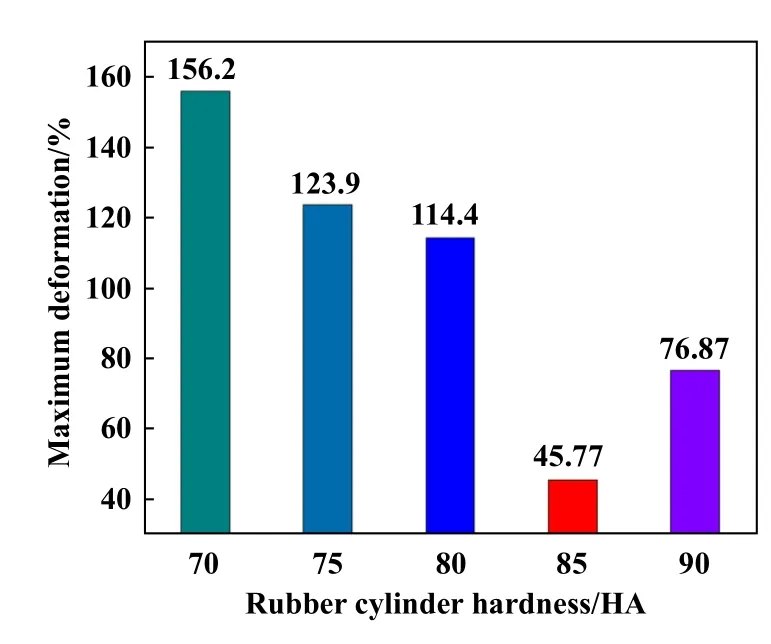
Fig.6 Maximum deformation of rubber cylinders with different hardness under the same maximum contact stress图6 最大接触应力相等情况下不同硬度橡胶筒的最大变形量
在近似相同的密封效果下,橡胶筒为85 HA时,最大变形量最小.再综合考虑肩凸现象对橡胶筒使用寿命的影响及密封特性分析,可以得出最优的橡胶筒硬度为85 HA.
3.2 橡胶筒在不同轴向长度下的密封性能分析
取橡胶筒轴向长度为80~200 mm,将橡胶筒轴向长度等分为80、100、120、140、160、180和200 mm,对管壁的接触应力进行对比分析.相同载荷下不同轴向长度的橡胶筒与管壁接触应力分布曲线如图7所示.橡胶筒与管道接触参数列于表4中.

表4 不同轴向长度橡胶筒与管道接触参数Table 4 Contact parameters between rubber cylinder and pipe with different axial lengths

Fig.7 Contact stress distribution curve between rubber cylinder and pipe wall with different axial lengths图7 不同轴向长度的橡胶筒与管壁接触应力分布曲线
对上述所获得的不同轴向长度的橡胶筒与管壁接触应力分布曲线图和橡胶筒与管道接触参数表进行分析,可得到如下结果:
(1) 当橡胶筒轴向长度为80、100和120 mm时,有效接触长度较短导致密封性能系数K较小,橡胶筒密封效果不佳.
(2) 随着橡胶筒轴向长度增加,最大接触应力和平均接触应力变化不大,密封性能系数K逐渐增大,密封性能越来越好.
(3) 橡胶筒最大Mises应力在轴向长度为200 mm时为22.37 MPa,影响橡胶的弹性恢复力.结合橡胶筒的密封特性分析及最大Mises应力对其弹性恢复力的影响,橡胶筒的最优轴向长度为180 mm.
3.3 橡胶筒在不同径向厚度下的密封性能分析
取橡胶筒径向厚度为40~70 mm,将橡胶筒径向厚度等分为40、45、50、55、60、65和70 mm,对管壁的接触应力进行对比分析.相同载荷下不同径向厚度的橡胶筒与管壁接触应力分布曲线如图8所示.橡胶筒与管道接触参数列于表5中.
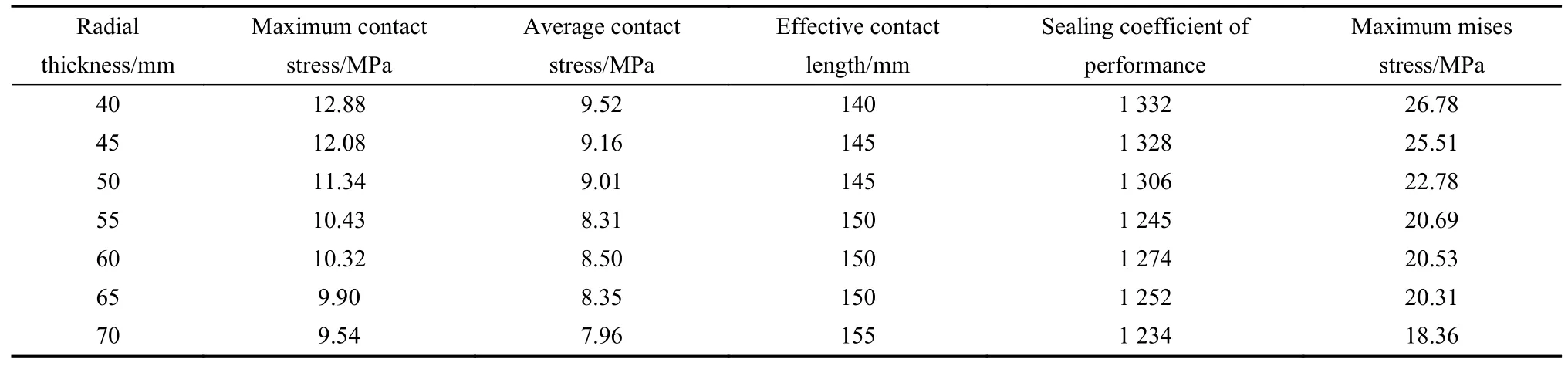
表5 不同径向厚度橡胶筒与管道接触参数Table 5 Contact parameters between rubber cylinder and pipe with different radial thickness
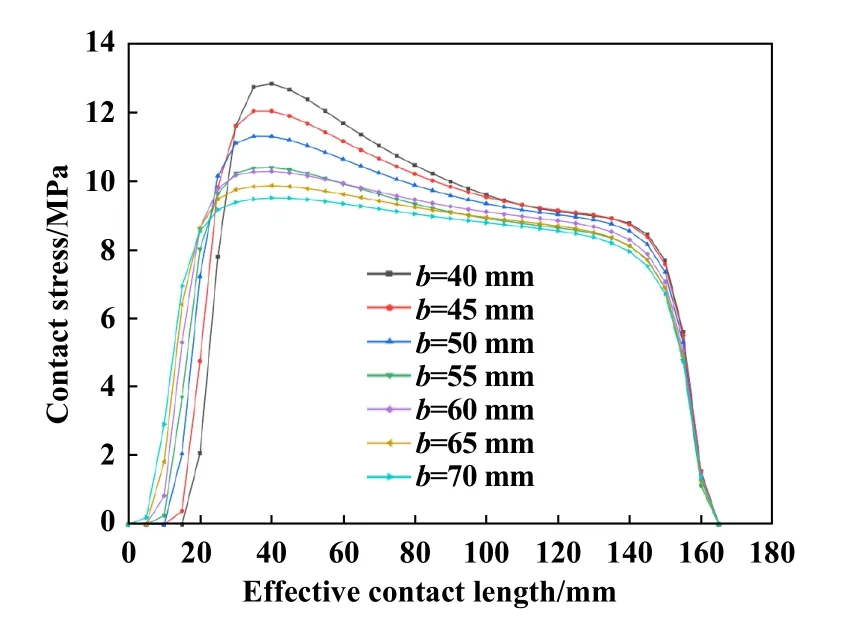
Fig.8 Contact stress distribution curve between rubber cylinder and pipe wall with different radial thickness图8 不同径向厚度的橡胶筒与管壁接触应力分布曲线
对上述所获得的不同径向厚度的橡胶筒与管壁接触应力分布曲线图和橡胶筒与管道接触参数表进行分析,可得到如下结果:
(1) 在相同的载荷下,随着橡胶筒径向厚度的增加,最大接触应力、平均接触应力和密封性能系数K逐渐减小.
(2) 橡胶筒径向厚度的变化对其密封特性的影响很小,但最大Mises应力变化较大,即对橡胶筒的损伤影响较大,结合密封特性和自身损伤分析可知橡胶筒的最优径向厚度为55 mm.
3.4 橡胶筒在不同倾斜边角下的密封性能分析
橡胶筒密封时不同的倾斜边角 α也会对其密封特性存在显著影响.首先设置范围在0°~45°之间,每间隔4°建立1个分析模型,相同载荷下不同倾斜边角橡胶筒管壁接触应力分布曲线如图9所示.橡胶筒与管道接触参数列于表6中.
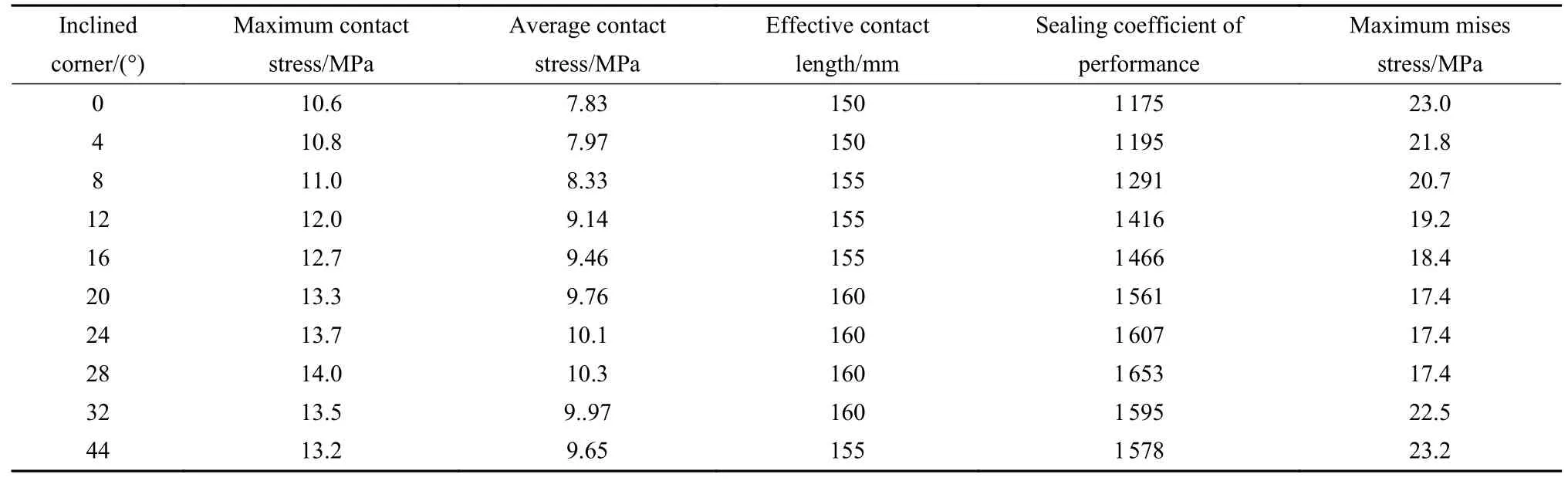
表6 不同倾斜边角橡胶筒与管道接触参数表Table 6 Contact parameters between rubber cylinder and pipe with different inclined corners
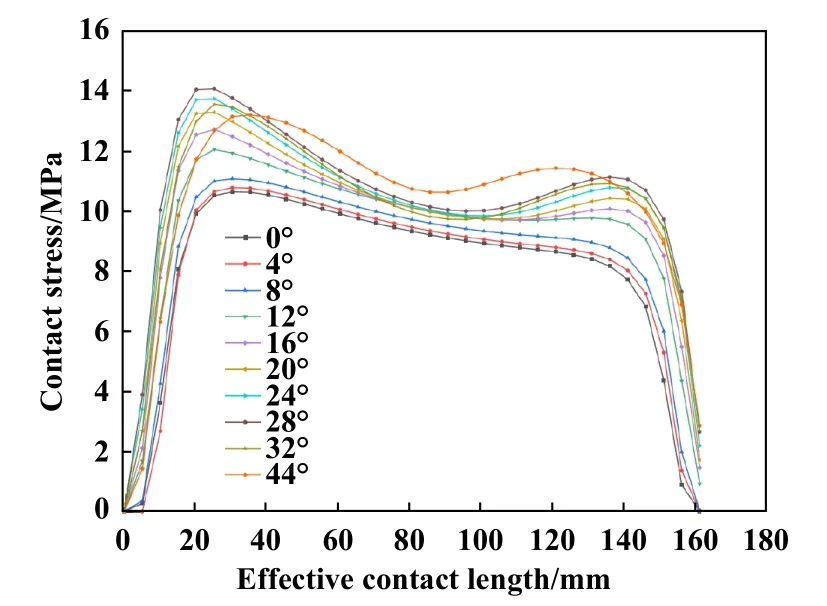
Fig.9 Contact stress distribution curve between rubber cylinder and pipe wall with different inclined corners图9 不同倾斜边角橡胶筒与管壁接触应力分布曲线
对上述所获得的不同倾斜边角的橡胶筒与管壁接触应力分布曲线图和橡胶筒与管道接触参数表进行分析,可得到如下结果:
(1) 在倾斜边角 α <20°时,随着倾斜角度增加,最大接触应力、平均接触应力和密封性能系数K均逐渐增大,在 α ≥28°时,最大接触应力、平均接触应力和密封性能系数K均随着倾斜角度增加而逐渐减小.表明橡胶筒的密封性能随着倾斜边角 α的增加先增大后减小.
(2) 在倾斜边角 α <20°时,随着角度增大,Mises应力值减小.α ≥20°时,随着角度增大,Mises应力值增大.在α=20°时橡胶筒Mises应力值最小,为17.39 MPa.在 α=28°时,橡胶筒Mises应力值为17.42 MPa,与最小值相差很小,结合橡胶筒的密封性能分析可知α=28°时应用效果最好.
4 管道封堵机器人橡胶筒密封特性试验研究
4.1 橡胶筒材料密封特性试验
4.1.1 试验方案
设计的橡胶筒材料试验原理如图10所示[29].将橡胶筒放入模拟压力管道容器中,压力试验机挤压橡胶筒变形贴合管道内壁,不同硬度橡胶筒的试验作用载荷列于表7中.当橡胶筒密封完成后,从进压口压入10 MPa油液,观察橡胶筒试验装置上端是否出现泄漏现象,验证橡胶筒的密封效果.最后,观察橡胶筒是否存在肩部突起和磨损等情况,选择形变损伤最小的硬度的橡胶筒为最优橡胶筒硬度.

表7 不同硬度橡胶筒试验作用载荷Table 7 Test load of rubber cylinders with different hardness
橡胶筒分为5种硬度,分别为70 HA、75 HA、80 HA、85 HA和90 HA,如图11所示.

Fig.11 Photograph of 70 HA~90 HA hardness rubber cylinder图11 70 HA~90 HA硬度橡胶筒照片
4.1.2 试验步骤
1) 将橡胶筒放入模拟压力管道容器中,盖上压力盖,放在压力试验机上,连接好液压管线与液压泵.
2) 开启压力试验机,控制其向下作用压力盖并挤压橡胶筒,橡胶筒向外膨胀贴紧管道内壁.
3) 停止压缩进程并稳压.开启手动液压泵,向橡胶筒下端缓慢打入10 MPa油液,然后稳压10 s.稳压过程中手动液压泵上的压力表读数如图12所示.

Fig.12 Manual hydraulic pump stabilizes 10 MPa without pressure drop图12 手动液压泵稳压10 MPa无压降
4) 试压油液退压,压力试验机再慢慢回升,更换不同硬度橡胶筒,重复以上步骤,共5组.
5) 记录各组试验过程的泄漏情况及橡胶筒受损情况.
4.2 橡胶筒密封试验结果与分析
试验以手动液压泵稳压过程中压力表数值稳定无压降判断橡胶筒是否实现了10 MPa的压力密封.图12中手动液压泵稳压10 MPa无压降表明,5种硬度橡胶筒在表7所列的载荷下均可实现10 MPa密封.如图13所示,观察橡胶筒侧面,硬度为70 HA和75 HA的橡胶筒出现明显裂缝.硬度为85 HA~90 HA时,侧面与初始形状相同.观察橡胶筒被压缩面,硬度为70 HA~80 HA时肩突现象最明显,85 HA的橡胶筒肩突现象最弱.硬度大于80 HA时,橡胶筒的应用效果更好.硬度越大,橡胶筒所需封堵力越大.结合仿真分析结果可知,管道封堵机器人橡胶筒的最优硬度为85 HA.

Fig.13 Compression test results of 70 HA~90 HA hardness rubber cylinder图13 70 HA~90 HA硬度的橡胶筒压缩试验结果图
5 结论
本文中以管道封堵机器人密封性能为基础.基于橡胶筒材料的高弹性和大变形特性,进行了橡胶筒单元力学分析.对橡胶材料进行了拉伸压缩试验,得到了橡胶材料的本构关系参数.建立出橡胶筒密封特性分析的有限元仿真模型.通过有限元仿真与试验分析,最终得出以下几点结论:
a.管道封堵机器人封堵作业过程中,橡胶筒与管壁之间的接触应力和密封性能系数的大小是评价封堵性能的关键参数.橡胶筒被压缩面的Mises应力是评价橡胶筒弹性回复力的关键参数,减小Mises应力有利于提高管道封堵机器人使用寿命.
b.随着橡胶筒的硬度增大,在相同载荷下,橡胶筒密封性能越弱,变形量越小.随着橡胶筒轴向长度增加,橡胶筒密封性能越好,但橡胶筒被压缩面Mises应力越大,橡胶筒肩凸较大.随着橡胶筒径向厚度减小,橡胶筒的密封性能越好,但橡胶筒被压缩面Mises应力越大.随着橡胶筒倾斜边角增加,橡胶筒的密封性能先增强后减弱,橡胶筒被压缩面Mises应力先减小后增大.
c.合理的优化橡胶筒结构参数可以有效提高管道封堵机器人工作寿命减小橡胶筒损伤变形,以提高管道封堵机器人的工作性能.经过橡胶筒密封特性与被压缩面Mises应力对比分析后得出最优的橡胶筒结构为L=180 mm,b=55 mm,α=28°,橡胶材料硬度为85 HA.
d.加工出70 HA~90 HA的5种硬度橡胶筒进行密封特性分析试验.试验结果表明,5种硬度橡胶筒分别在所对应的载荷下均满足10 MPa密封要求,85 HA硬度的橡胶筒侧面及被压缩面损伤较少,密封效果最好.
本文中开展的橡胶材料单轴拉伸压缩试验及其本构模型拟合为管道封堵机器人设计人员针对橡胶材料的选择提供了参考.帮助管道封堵机器人设计人员考虑从橡胶筒与管壁间的接触应力和密封性能系数去评价橡胶筒的密封性能,从橡胶筒被压缩面的Mises应力去评价橡胶筒弹性回复力,有利于帮助设计人员开发出高寿命、高可靠性的管道封堵机器人.橡胶筒材料密封特性试验研究考虑了管内高压和大尺寸的橡胶筒,具备一定的通用性,能够指导设计人员开展不同型号管道封堵机器人和不同管内压力的橡胶筒密封试验.
同时,设计了1套微型液压控制系统,相应地开展了液压系统工况分析,研究了调压回路、节流调速回路和锁紧回路的设计以及液压缸、微型液压泵、蓄能器、三位四通换向阀和溢流阀等元器件的选型计算.针对设计的微型液压控制系统,后续将利用Amesim/Simulink联合仿真,开展无控制器、PID控制和模糊PID控制的对比分析,并开展相关的试验研究以实现橡胶筒密封外部加载力的精确控制.
