转向架齿轮箱动力学建模与故障量化分类方法研究
2023-10-13谢劲松唐昀昭阳劲松王田天
谢劲松,唐昀昭,阳劲松,王田天
(1. 中南大学 交通运输工程学院,湖南 长沙,410083;2. 中车株洲电力机车有限公司,湖南 株洲,412001)
转向架齿轮箱是列车走行部的重要组成部分,在高速度、重负载的条件下长时间工作,故障发生概率较高[1]。当前,我国轨道车辆检修制度以计划预防修体制为主,该制度可能导致使用周期内齿轮箱出现的故障难以及时被发现并处理,进而引发安全事故。因此,准确监测并判别转向架齿轮箱故障及其类型,为维护人员提供决策信息,避免安全事故的发生,具有重要的工程应用价值。齿轮系统振动特性分析和诊断方法研究是解决上述问题的关键。
在齿轮系统的动力学建模和振动特性研究方面,国内外学者都已开展了卓有成效的工作。自20世纪60年代,TUPLIN[2]首次提出等效啮合刚度的概念以来,研究者们开始建立不同的齿轮系统动力学模型以探究其振动特性。冯娜娜等[3]对各种齿轮故障的物理特征进行了分析,提出了裂纹、断齿和齿面剥落等几种故障齿轮啮合刚度的计算方法。强仕杰等[4]对不同类型的断齿齿轮做出了区分,并提出了相应的啮合刚度计算方法。代鹏等[5]建立了齿面剥落故障的齿轮动力学模型,研究了剥落故障发展到不同时间阶段对整个系统动力学特性的影响。CUI等[6]提出了一种齿面剥落故障齿轮啮合刚度计算方法,研究了剥落部分的尺寸对齿轮啮合刚度的影响。YI等[7]建立了一种考虑齿间间隙时变特性的齿轮系统动力学模型。此外,相关的实验研究也被学者们所关注,用以验证建立模型的正确性与实用性。肖凌俊等[8]开展了齿轮箱故障模拟试验,采集了齿轮箱轴承正常、点蚀、磨损和外圈故障4种工况的齿轮箱振动响应以验证诊断方法的有效性。杨文哲等[9]开展了齿轮箱齿轮故障和轴承故障试验研究,获取了4种齿轮故障及3 种轴承故障的振动信号。LIN 等[10]进行了偏心曲面齿轮传动系统的振动试验,证明了偏心曲面齿轮传动系统的动力学模型的正确性。上述研究者从齿轮系统的振动特征出发,进行模型仿真和实验,为齿轮系统的故障诊断提供了理论依据。进一步,针对细化的故障类型如齿面擦伤、缺角、齿根裂纹等,建立其精确动力学模型,分析其振动响应特征,为故障的量化分类提供先验信息,是实现齿轮故障类型精确诊断的重要途径。
现有的齿轮故障诊断方法主要分为两大类:一类是基于故障机理和信号处理的特征提取诊断方法,另一类是数据驱动的机器学习和深度学习诊断方法。在数据驱动的诊断方法方面,ZHAO等[11]将多任务深度学习模型应用在轴承和齿轮的故障诊断上,准确判断了齿轮和轴承在各种工况下的故障。YANG等[12]提出了一种基于小波神经网络的误差反向传播粒子群优化算法,并将其用于裂纹故障齿轮系统诊断。郗涛等[13]提出了一种基于参数优化的变分模态分解与卷积神经网相融合的故障诊断方法,成功对六类故障齿轮系统进行诊断。陈科等[14]构建了一种基于卷积神经网络和改进堆叠降噪自动编码器的混合网络模型,提高了模型诊断的正确性。数据驱动的智能诊断方法能够自动地对不同的故障齿轮系统进行诊断,但诊断的准确性往往依赖于样本数和样本质量,而实际的工程运用中,转向架齿轮箱的使用环境多变且复杂,载荷的变化频繁且显著,数据分布差异较大,且结果的可解释性仍有待提升。
在故障样本有限、故障模式不全的情况下,基于故障机理和信号处理的诊断方法具有更大的优势。张海涵等[15]通过分析振动信号频谱图的边频特征和幅值特征,来对断齿和磨损故障齿轮进行诊断。宋建等[16]使用小波算法和EMD 分解算法,去除了振动信号中的高频稳态频率成分,确定了齿轮断齿故障信号的频率。江星星等[17]基于VMD 分解的特性,提出了一种基于收敛趋势变分模式分解的齿轮箱故障诊断方法。WANG 等[18]提出了一种频域能量特征重构的轨道车辆齿轮箱轴承故障诊断方法。CHENG等[19]提出了一种针对状态退化的齿轮系统故障诊断方法,并通过旋转机械轴承数据集和某型高速铁路行走齿轮系统的温度数据验证了提出方法的有效性。WANG 等[20]提出了一种改进变分模态分解参数的方法,并成功地应用于风力发电机齿轮箱的故障诊断,提取得到了齿轮箱的复合故障特征。基于故障机理和信号处理方法构建的诊断方法在少样本情况下具有显著的优势,其结果具有明确的物理意义和可解释性,在工程应用中具有重要地位和意义。振动机理分析确定的齿轮故障特征频率,实现了正常和故障状态的显著区分。然而,针对细化的擦伤、缺角、齿根裂纹等具体故障类型,特征频率尚不能进行显著区分。
针对上述研究和存在问题,本文提出一种齿轮故障的波峰计数量化分类方法,以充分利用齿轮的故障机理先验信息,实现细化的擦伤、缺角、齿根裂纹等具体故障类型的准确判别,避免了智能诊断方法对大量数据样本的依赖;从齿轮系统振动特性出发,建立正常及擦伤、缺角和裂纹等齿轮状态的精确动力学模型,基于模型得到齿轮系统正常及故障的振动特征信号。进一步地,基于仿真信号的频域特征,提出一种基于波峰计数的细化故障类型精确分类方法,实现正常及擦伤、缺角和裂纹的准确判别。最后,设计并开展转向架齿轮箱故障模拟试验,验证所建立模型的正确性和提出方法的有效性。
1 齿轮系统动力学建模
首先建立齿轮系统横向振动-扭转振动耦合动力学模型。为了精确获得齿轮不同故障类型的振动响应特征,从故障的物理特征出发,考虑弯曲、剪切、接触和径向压缩综合力学效应,建立了擦伤、缺角和裂纹等齿轮故障的精确啮合刚度模型,最终形成了可量化区分齿轮故障类型的动力学模型。
1.1 齿轮系统振动分析模型的建立
齿轮啮合系统的模型示意图如图1所示,将啮合齿轮副看作一个具有质量、弹性和阻尼的振动系统,将传动轴、支承轴承和箱体等部件弹性变形的影响加入振动模型之中,将其刚度特性与阻尼以等效值进行表示[21]。
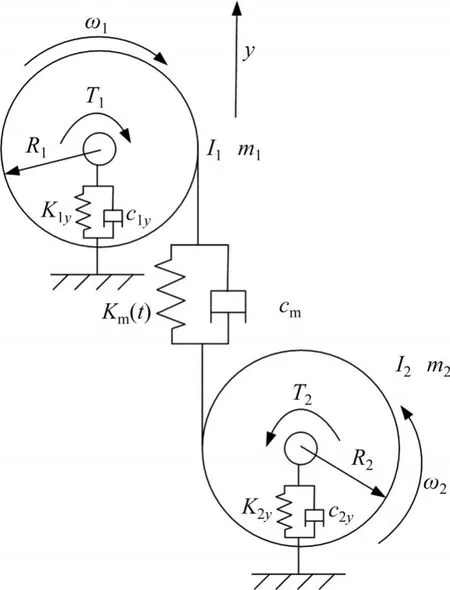
图1 齿轮系统横向振动-扭转振动耦合简化模型Fig. 1 Bending-torsion coupling dynamic model of gear system
不考虑齿面摩擦,所建立的动力学模型为一个二维平面振动系统,具有4个自由度,即主、从动轮的转动和垂直轴向的振动,根据横向振动-扭转振动耦合简化模型,构建其动力学方程如下[22]:
式中,y1和y2分别为主、从动齿轮垂直轴向的振动位移;θ1和θ2分别为主、从动齿轮的角位移;上标⋅和⋅⋅分别表示一阶和二阶微分;m1和m2分别为主、从动齿轮的质量;R1和R2分别为主、从动齿轮的基圆半径;I1和I2分别为主、从动齿轮的转动惯量;T1和T2分别为主、从动齿轮所受到的外加扭矩;c1y和c2y分别为主、从动齿轮的平移振动阻尼系数;K1y和K2y分别为主、从动齿轮的平移振动刚度系数;Km和cm分别为齿轮副的综合啮合刚度与综合阻尼。
1.2 正常齿轮系统综合啮合刚度计算
轮齿综合啮合刚度指的是在轮齿啮合过程中啮合区每一对轮齿的综合效应,与齿轮副啮合轮齿的弹性变形以及齿轮副的重合度密切相关,不同类型齿轮系统的啮合特性都通过综合啮合刚度Km对整个齿轮系统产生影响。
在齿轮的啮合过程中,系统能量储包括赫兹能、弯曲能、剪切能以及径向压缩能4个部分。因此,综合啮合刚度可以通过赫兹接触刚度、弯曲刚度、剪切刚度和径向压缩刚度来进行表示,计算公式如下[23]:
式中:kh、kb、ks和ka分别为沿啮合力F方向的赫兹接触刚度、有效弯曲刚度、剪切刚度和径向压缩刚度;下标1 和2 分别表示主、从动齿轮;E为弹性模量;L为齿轮副轮齿啮合长度;v为泊松比;α1为啮合点的啮合瞬时压力角;α2为啮合点的最小压力角。轮齿受力示意图如图2所示。
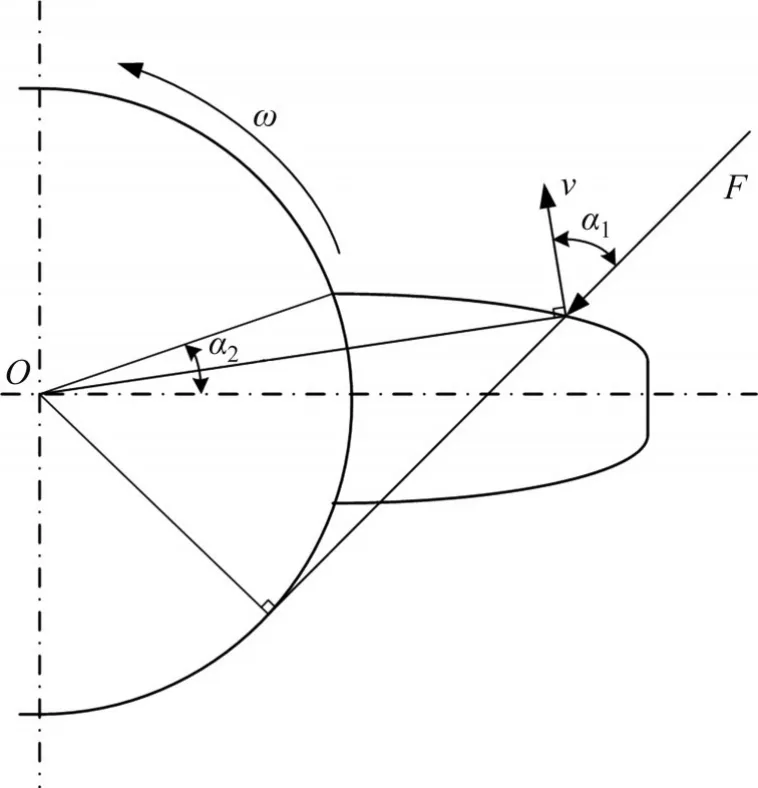
图2 轮齿受力示意图Fig. 2 Sketch of forces on tooth of cogwheel
从图2可知,在啮合过程中,随着主、从动齿轮的转动,啮合点的位置也在齿面上周期性移动。不同时刻齿面啮合点位置不同,通过压力角α1对上述刚度系数产生影响。因此,综合啮合刚度Km是一个时变量。压力角α1和齿轮转角θ的关系为
其中,α0为啮合初始位置的压力角。
通过式(9)可以计算得到一对轮齿在啮合过程中的综合啮合刚度。直齿圆柱齿轮副的啮合过程是由单齿啮合和双齿啮合交替组成的。在双齿啮合区段,啮合齿对1 与啮合齿对2 可以视作2 个刚度分别为Km1和Km2的弹簧的串联,啮合综合刚度为
在整个啮合过程中,单齿啮合部分和双齿啮合部分的占比与齿轮副的重合度有关。
1.3 故障齿轮系统综合啮合刚度计算
刚度激励为本动力学模型的激励源,所有齿轮故障都通过时变啮合刚度对整个系统的振动特性产生影响。从各故障的物理特性出发,基于工程实践中的故障统计经验和分布规律,设计了不同损伤类型的等效啮合刚度建模方法,并建立故障齿轮系统动力学模型。
1.3.1 擦伤齿轮系统综合啮合刚度计算
对于高速和重载轨道交通的转向架牵引齿轮传动系统,当润滑条件时,两个啮合的齿面在相对滑动时油膜破裂,在摩擦和表面压力的作用力下产生高温,使处于接触区的金属出现局部熔焊,并在齿面上形成垂直于节线的划痕和胶合,这种故障形式称为齿轮擦伤,其示意图如图3所示,图中,R为齿轮基圆半径,r为任一时间啮合点到齿轮基圆圆心的距离。
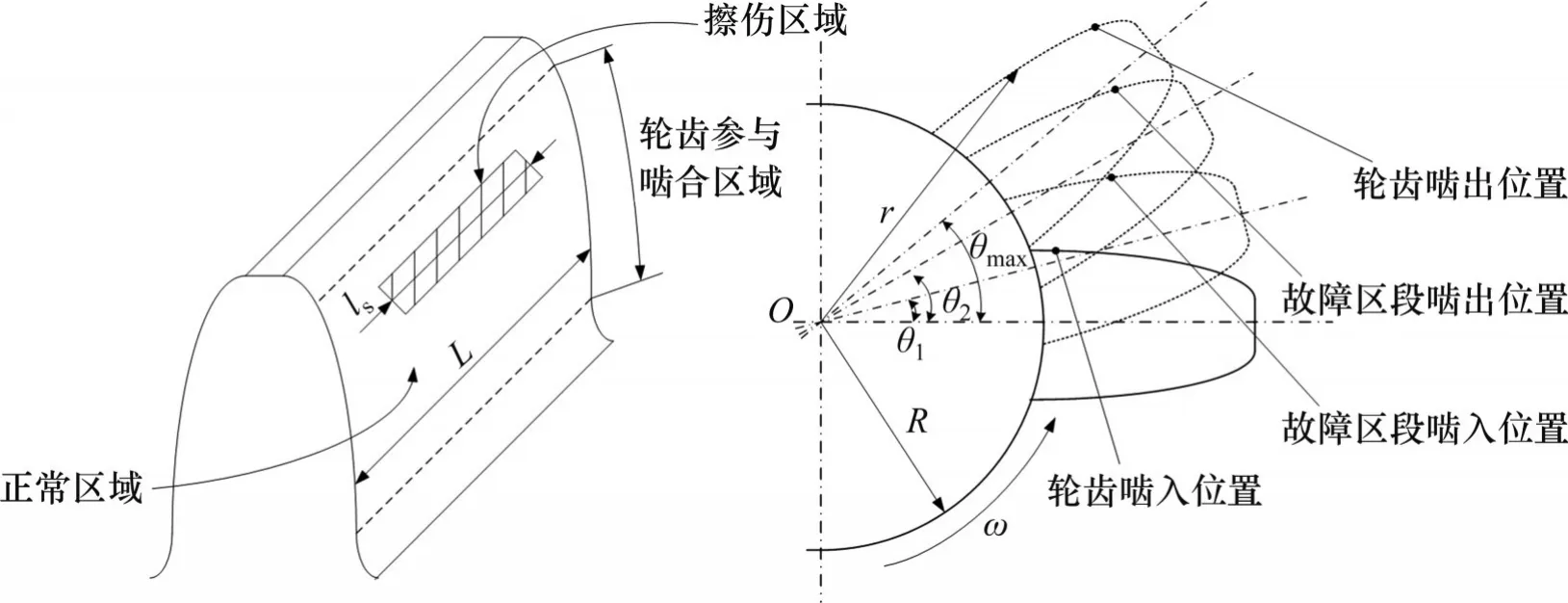
图3 擦伤轮齿示意图Fig. 3 Sketch of scraped tooth
擦伤故障通常在齿面上以近似矩形区域出现,且不同于齿面剥落,故障区域只存在于齿面上,对故障轮齿的惯性矩和质量分布等因素影响很小。因而对擦伤故障轮齿,仅考虑故障对赫兹接触刚度产生影响,忽略其对剪切刚度、弯曲刚度和压缩刚度等参数的影响。
当故障轮齿参与啮合时,擦伤轮齿主要通过改变故障区段的轮齿的有效接触长度来对整个赫兹接触刚度产生影响。根据压力角的定义,轮齿上任一啮合点的压力角α计算方法如下:
将故障轮齿啮入时刻的转角定义为θ=0°,在确定压力角后便可以使用式(10)确定图示各啮合状态切换位置的齿轮转角。根据擦伤区域的位置关系,可计算得擦伤区域的啮入角θ1和啮出角θ2。而齿轮转角范围在[0,θ1)或(θ2,θMax]时,轮齿啮合至无故障区域,此时,有效啮合长度即为齿轮的齿宽L;当齿轮转角范围[θ1,θ2]时,轮齿啮合至故障区域时,故障区段的沿齿宽方向的长度为ls,则故障区段的有效啮合长度为:
对于图3中擦伤区段的故障轮齿,其赫兹接触刚度计算方法如下:
将计算得到的赫兹接触刚度代入式(9)便可以得到擦伤轮齿的综合啮合刚度。
1.3.2 缺角齿轮系统综合啮合刚度计算
在重载条件下,齿轮往往会因受到的载荷超过强度极限而断裂,形成缺角[4]。除了外加载荷作用会引起缺角外,在使用过程中,任何严重的冲击、偏载以及材质不均都可能会引起缺角。缺角故障往往位于轮齿齿顶区域,示意图如图4所示。
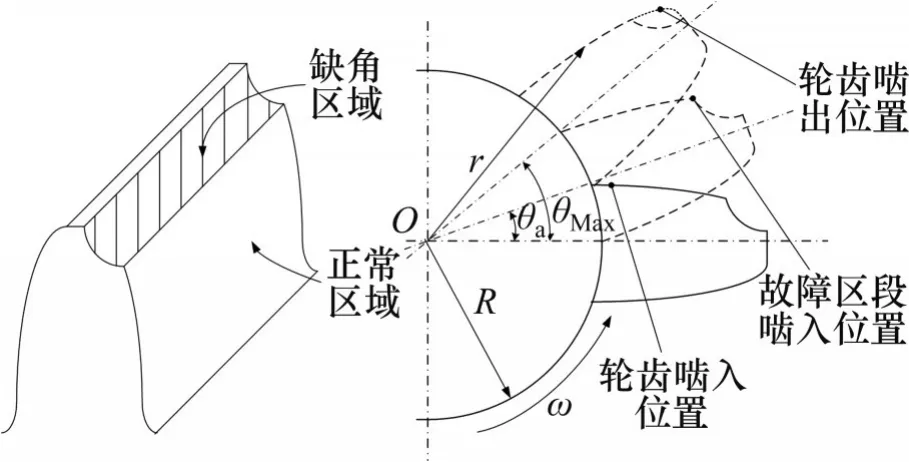
图4 缺角轮齿示意图Fig. 4 Sketch of notched tooth
缺角故障会使得轮齿在啮合到故障区段时啮合刚度急剧下降。当缺角故障严重时,在故障段相当于少了一个轮齿进行啮合,因此会引起系统的振动,对系统的平稳运行起到极大的影响。由于齿轮副的固有特性,若该种齿顶缺角故障位于主动齿轮上,则会在该故障轮齿啮合过程将要结束时对其啮合刚度产生影响;若该种齿顶缺角故障位于从动齿轮上,则该故障会在轮齿啮合过程刚开始时对其啮合刚度产生影响。
通过式(12)确定啮合过程中图示各啮合状态切换位置的压力角,再通过式(10)便可以确定齿轮的转角θ。根据缺角的几何位置和参数时,即可计算得到区角的啮入角θa。由于缺角段无法参与正常的轮齿啮合,因此,该轮齿在参与啮合时,在缺角故障段,转角θ∊[θa,θMax],在无故障段,转角θ∊[0,θa],啮合刚度函数为
1.3.3 裂纹齿轮系统综合啮合刚度计算
转向架齿轮箱在高速工作的条件下,轮齿受到脉动循环交变的弯曲应力。由于齿轮的特殊形状,使得轮齿根部最易产生应力集中,发展成为齿根裂纹。随着裂纹的发展,最终造成轮齿断裂,给列车运行造成极大的隐患。出于安全考虑,在齿根裂纹出现的阶段就应当被识别并处理。当裂纹出现时,故障轮齿的有效惯性矩和横截面面积将发生变化[3]。将裂纹形状简化为直线后,故障轮齿的受力如图5 所示,图中,q1为裂纹深度;β为裂纹交角;Rb1为故障齿轮的基圆半径。
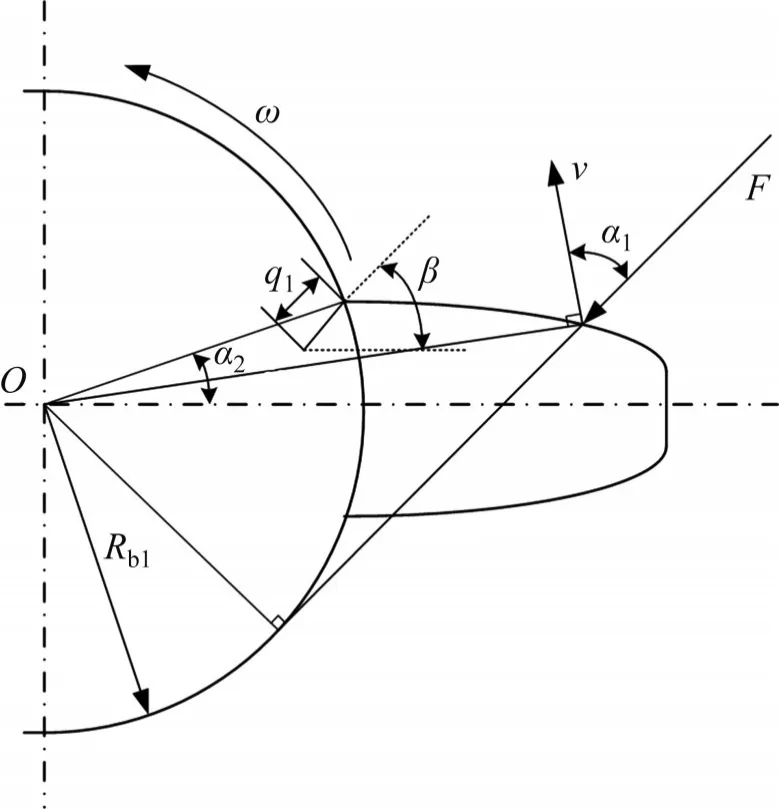
图5 裂纹轮齿受力示意图Fig. 5 Sketch of forces on cracked tooth of cogwheel
裂纹轮齿有效弯曲刚度和剪切刚度分别为
将式(16)和式(17)代入式(9)便可以计算得到裂纹故障齿轮的综合啮合刚度。
1.4 模型仿真结果
以转向架结构形式和传动关系为依据,为便于模型验证,仿真中结构参数设置为转向架的缩比,具体如表1所示。以上述结构参数,结合构建的正常啮合、擦伤、缺角、齿根裂纹4种状态的刚度模型,通过积分运算得到啮合过程中各齿轮的啮合刚度变化曲线如图6所示,其中,各故障均位于主动齿轮的某一轮齿上,裂纹故障轮齿的齿根裂纹深度q1为3 mm,裂纹交角β为60°;擦伤轮齿的矩形擦伤故障区段沿齿宽方向的长度ls等于齿宽L,啮入故障区段时啮合点到齿轮基圆圆心的距离r1为42.1 mm,啮出故障区段时啮合点到齿轮基圆圆心的距离r2为43.4 mm;缺角轮齿啮入故障区段时啮合点到齿轮基圆圆心的距离ra为43.2 mm。
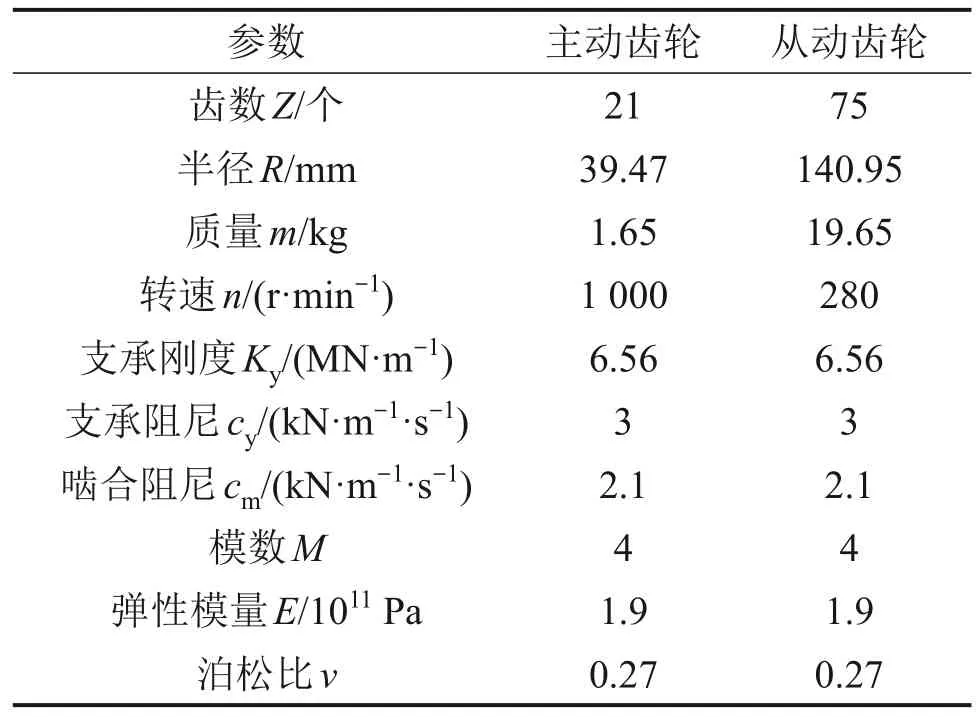
表1 动力学模型关键参数Table 1 Parameters of dynamic model
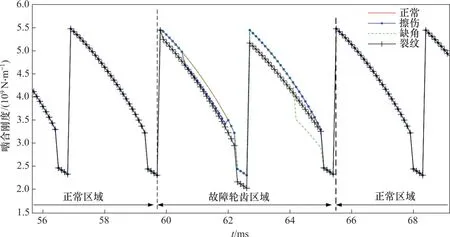
图6 不同齿轮啮合刚度对比Fig. 6 Comparison of meshing stiffness of different gears
从图6可以看出,在单齿对啮合和双齿对啮合状态切换时,综合啮合刚度变化显著,并且即使啮合齿数不变,由于啮合角度的变化,其刚度也是随时间渐变的。在正常区域,各齿轮的啮合刚度曲线重合,表明其刚度一致。在故障齿轮参与啮合的区域,由于故障的引入,其啮合刚度的曲线存在较大差异,该差异实现了对不同故障类型的准确表征,以进一步引入到动力学模型中实现不同故障类型的振动响应特征分析。
将上述不同故障状态的综合啮合刚度代入构建的齿轮系统动力学模型中,采用四阶龙格库塔方法对微分方程进行求解,得到不同故障类型齿轮系统中小齿轮垂向振动加速度响应,如图7 所示。仿真中,主动轮转速为1 000 r/min,因此,频谱中啮合频率frd=350 Hz的幅值很大,与实际齿轮系统的振动特征相符。
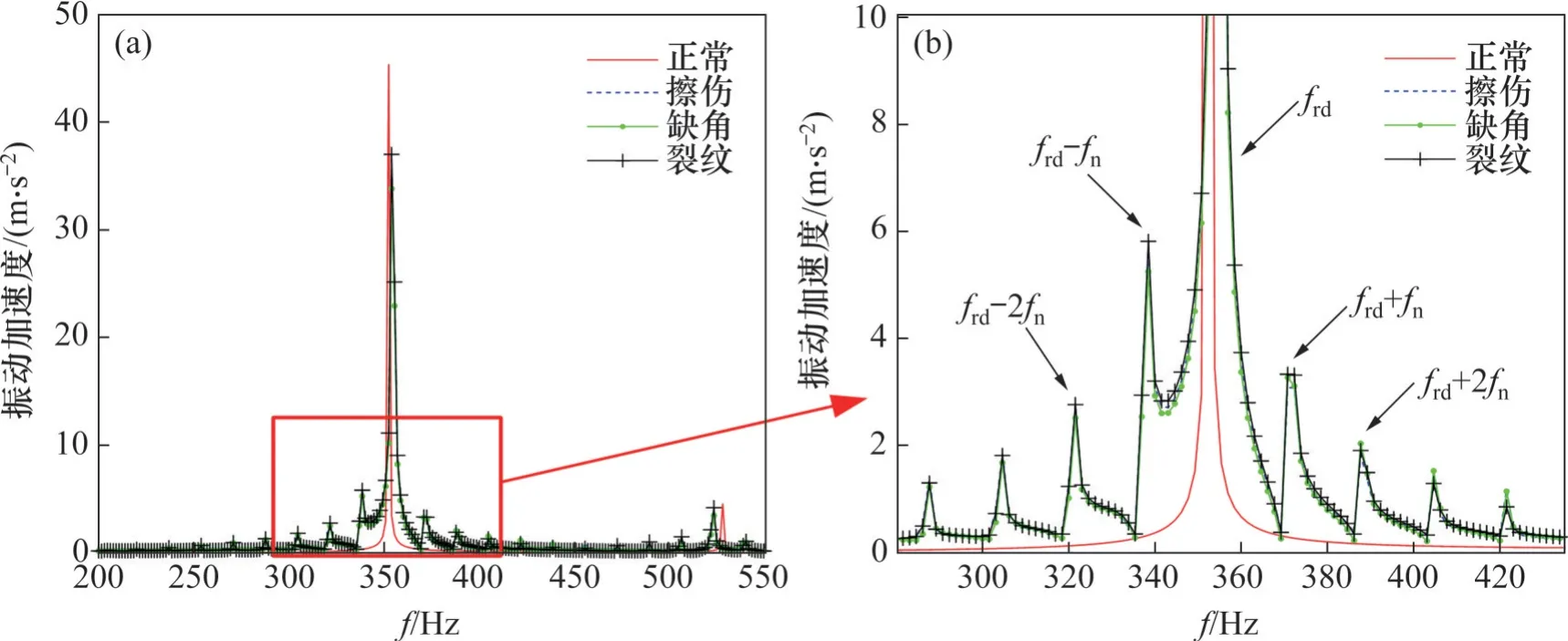
图7 不同故障类型齿轮系统垂向振动加速度频域信号Fig. 7 Vertical vibration acceleration spectrums of different gear systems in frequency domain
对于故障齿轮系统,由于擦伤、裂纹、缺角等故障均存在于主动齿轮的某一个轮齿上,因此主动齿轮每旋转1 周,故障轮齿就会参与1 次啮合。振动响应中产生以啮合频率为载波,以主动齿轮的转频为调制波的幅值调制现象。在频谱图上,其频谱特征具体表现为:啮合频率frd两侧出现边频成分,且各边频成分(ifrd±j·fn,i=1,2,3;j=1,2,3)之间的频率间隔等于主动轮的转频fn。该特征当前已被验证并广泛应用于齿轮的故障判别中。
上述边频特征虽然实现了正常和故障的区分,但对于细化的擦伤、缺角、裂纹等故障类型,尚不能定量化识别。
2 波峰计数齿轮故障诊断方法
从图6可以看出,不同故障类型对啮合刚度的影响程度不一样。从图7可以看出,故障对啮合刚度的影响体现在振动响应中即啮合频率两侧出现复杂的边频成分。由于不同故障类型导致的边频成分数不同,因此,从频带成分计数的角度出发,通过构建频带波峰计数的方法,对不同故障类型的波峰计数进行统计,实现故障类型的精确辨别。
2.1 方法提出
波峰计数齿轮故障诊断方法的思路是截取啮合频率及周边频段信号作为诊断信号,再合理设置阈值范围,统计不同类型的诊断信号超过该阈值的波峰数量,其流程如图8所示。
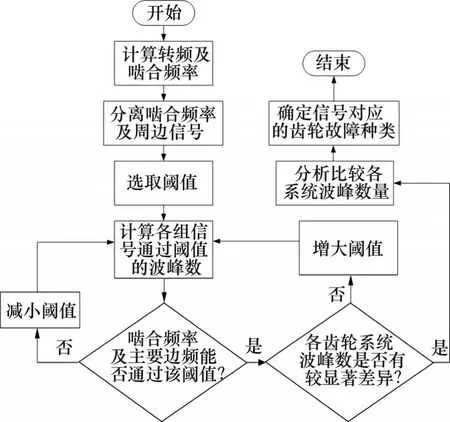
图8 波峰计数诊断方法流程Fig. 8 Flow chart of peak count diagnosis method based on threshold
该诊断方法的具体步骤如下。
1) 以少数的典型故障样本作为输入,获取齿轮系统转频fn、计算其啮合频率frd。
2) 在确定啮合频率后,通过小波分析或滤波等方法,分离得到目标频段的诊断信号;目标频段应当包含啮合频率及啮合频率周边大多数的边频频段,一般可以选择frd±5fn频段范围的信号。
3) 先初步选取阈值,后续再根据诊断效果对阈值进行调整。
4) 计算各组信号通过阈值的波峰数。
5) 判断啮合频率及主要边频是否通过该阈值。以第二步中选取频段范围为frd±5fn为例,此时测试的目标频率为啮合频率frd及两侧的10 个边频,共11 个波峰。若各组信号通过阈值的波峰数远远少于11,则说明阈值选择过高,多数特征频率的波峰都未被计数,应当适当减小阈值。
6) 对比各齿轮波峰数是否有显著差异。以frd±5fn范围频段为例,若各齿轮系统测得通过阈值的波峰数远大于11,则说明此时有很多噪声的波峰被纳入计算,诊断误差较大;若各组齿轮系统测得通过阈值的波峰数虽未大于11,却十分接近,则说明此时阈值选择过低,所有的特征频率波峰均通过了阈值,无法对不同齿轮系统的振动信号进行区分。当出现上述2种情况时,都应当适当增大阈值,直至各齿轮系统信号波峰数出现显著差异。
7) 统计分析合理阈值范围内,通过阈值的波峰数量,对不同齿轮系统进行区分诊断,确定具体的故障类型。
啮合频率可以通过转频和啮合齿数进行计算得到,为确保诊断的精确性,分离得到的诊断信号应当包含啮合频率周边大多数的边频。若进行区分的各齿轮系统故障严重程度相差较大,则可以适当减小测试频段的范围;反之,则应当适当增大测试频段的范围。
所提出的波峰计数诊断方法的重点在于阈值的选择。由于该方法分析的对象为啮合频率及周边信号,在理想状态下,希望通过阈值的信号波峰均为啮合频率及其边频。因此,阈值的选择不能过低,使得其他信号成分的波峰也高于阈值,影响诊断的精确性。同时,阈值的选择也不能过高,使特征频率即啮合频率和边频中的大部分波峰都低于阈值,导致故障诊断无法有效进行。实际操作时,合适的阈值应当既能够对不同故障的齿轮信号有所区分,又要保证大多数特征信号的波峰没有被漏算。
2.2 基于仿真数据的方法验证
基于不同故障类型的仿真数据,对提出的波峰计数齿轮故障分类方法进行验证。所构建的动力学仿真模型中,主动轮转速为1 000 r/min,主动轮齿数为21,则啮合频率frd为350 Hz,主动轮转频fn为16.67 Hz。选取各系统从动轮频域信号中的250~450 Hz 频段作为诊断信号,再通过设置不同范围的阈值ts,计算各阈值下不同故障类型的波峰数,结果如表2所示。

表2 不同阈值的波峰计数Table 2 Number of peaks under different thresholds
从表2 可以发现,当阈值ts小于0.04 时,各故障系统的波峰数十分相近,难以对具体故障类型做出区分;当阈值ts大于0.12时,每种信号能取到的波峰数都很少,说明此时大部分特征频率的波峰都未被计数,诊断依据不足。因此,合适的阈值ts范围为0.04~0.12。在此范围内对频带进行波峰计数、并取计数的平均值,结果如图9所示。
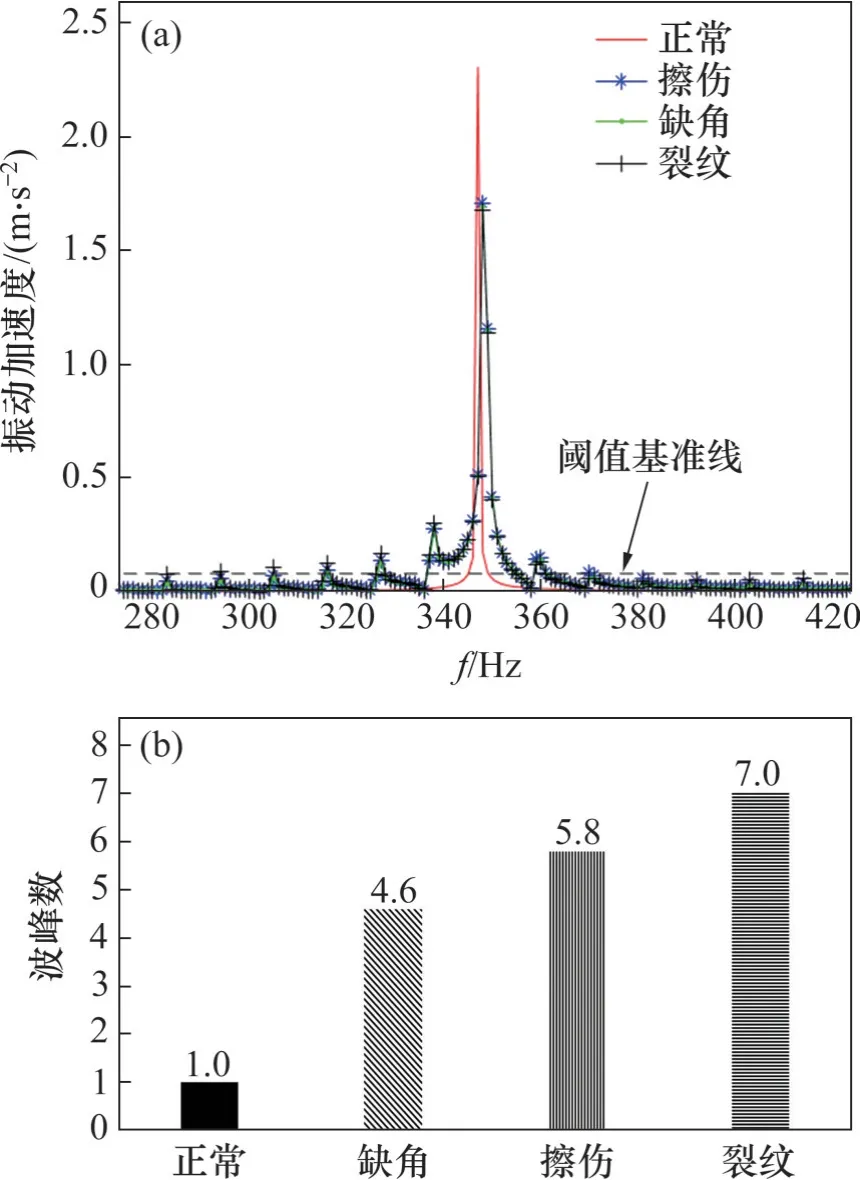
图9 波峰计数诊断方法的仿真验证Fig. 9 Verification of peak count diagnosis method based on simulation
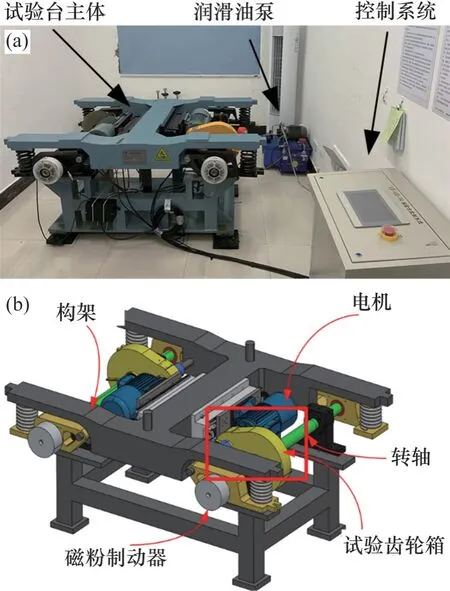
图10 转向架试验台Fig. 10 Test-bed of Bogie
从图9可以看出,不同故障类型的诊断信号通过阈值的波峰数量之间存在着较明显差异。正常齿轮在选取的阈值范围内,通过阈值的只有啮合频率的波峰,故其波峰数为1,而其他不同故障类型导致的边频成分不同,因此,其通过阈值的波峰数不同,其波峰数从多到少依次为裂纹、擦伤、缺角。
上述结果表明,在以故障齿轮系统精确模型的仿真信号为对象时,所提出的基于波峰计数齿轮诊断方法能够较好地对具体故障类型做出判别。
3 转向架齿轮箱故障模拟试验与诊断方法验证
针对建立的齿轮动力学模型和故障齿轮的结构参数,设计转向架齿轮箱故障模拟试验,采集不同故障类型的振动响应信号,对动力学模型故障特征的准确性和波峰计数故障分类方法的有效性进行验证。
3.1 齿轮箱故障模拟试验
3.1.1 试验系统介绍
转向架高保真试验台主要由控制系统、润滑油泵、台身、380 V交流电动机、转轴、一级减速齿轮箱(主、从动齿轮、箱体和滚动轴承)以及磁粉制动器等部件构成,其控制系统能够实现试验台的一体化控制,实现调节电机转速、模拟加减速过程、控制负载扭矩等功能,模拟多数应用场景下转向架的动力学特性。为了尽可能地接近真实的转向架结构,试验台台身按照转向架构架等比例设计制成,与实际工程应用中所使用的转向架有着相似的传动结构和力学性能。试验台齿轮箱为一级直齿圆柱齿轮箱,能够通过更换主动齿轮来模拟不同类型的齿轮故障。
数据采集系统如图11 所示,其中,传感器为压电式传感器,(20±5) ℃时灵敏度为100 mV/g;量程范围为±50 g;频率响应范围为0.5~5 000 Hz;HD9200多通道数据采集仪共有16个内置抗混叠滤波器的信号输入通道。试验中,由加速度传感器获取试验台的振动加速度,通过HD9200多通道数据采集仪将信息转化为数字信号输入到计算机中,通过采集控制与数据分析软件来实现采集得到数据的显示、存储、分析和可视化。

图11 数据采集系统Fig. 11 Data acquisition system
3.1.2 试验过程
为了验证模型的正确性,各齿轮试件的故障形式和故障程度与动力学模型的相关参数一致,如图12所示。齿面擦伤故障通过挫伤的方式加工,故障区域大致为一条平行于齿厚方向的细长矩形区域,有肉眼可见的擦伤痕迹存在;缺角故障通过铣削的方式加工,齿顶部铣削宽度约为整个齿顶宽度的1/3;齿根裂纹故障采用线切割的方式加工,裂纹交角约为60°,裂纹深度为齿根宽度的30%,约为3 mm。

图12 正常及故障齿轮试件Fig. 12 Normal and fault gear specimens
主动轮和从动轮啮合过程的振动直接通过从动轮的输出轴即车轴传递至两侧的轴箱轴承,而转臂则是轴箱轴承的固定位置,因此考虑到测点安装的可行性和测点对故障信号的敏感性,将振动加速度传感器安装在试验台两侧的转臂上,测点布置示意图如图13所示。
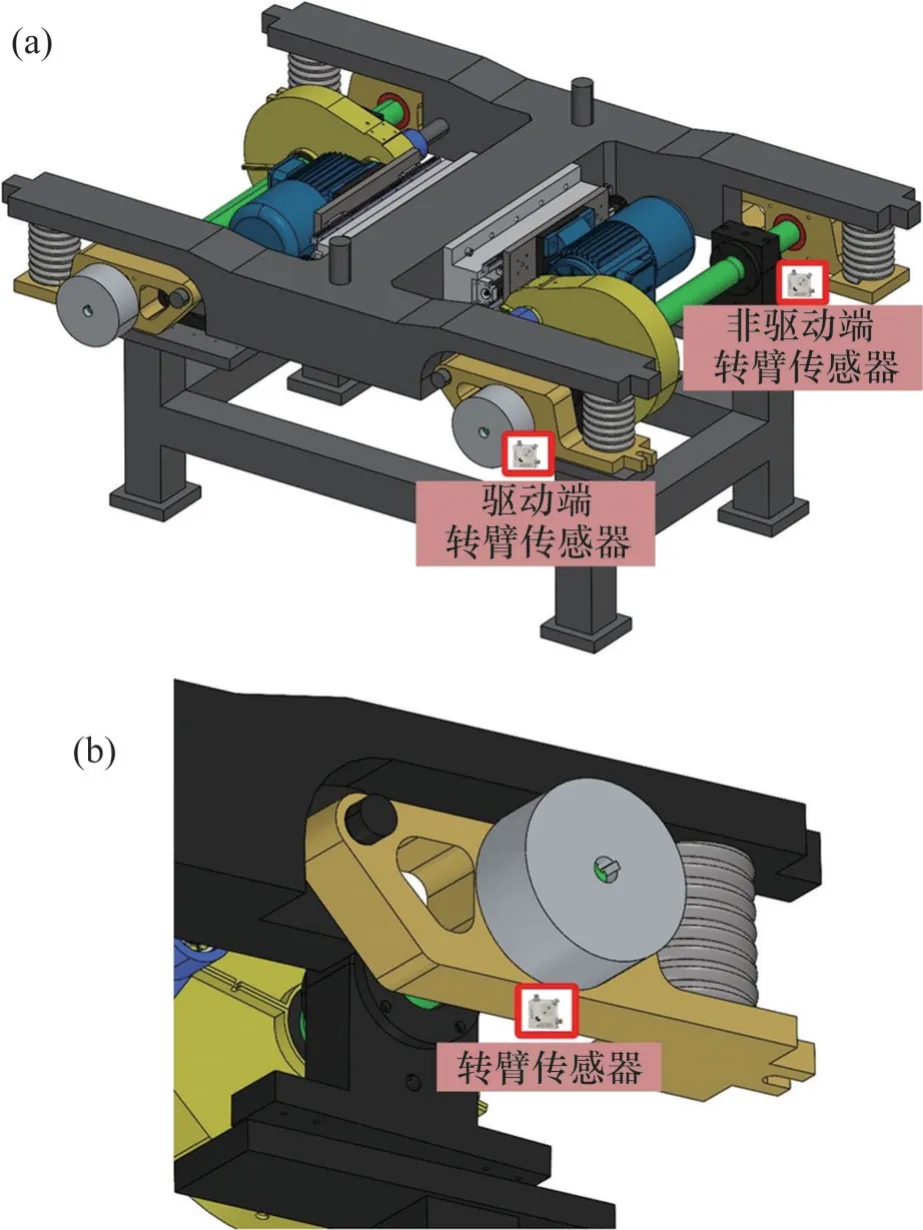
图13 测点布置示意图Fig. 13 Layout of measuring points
采样率为12 kHz,每种工况采样5 s。为了消除误差,在同一条件下进行4次重复试验,采集得到不同故障类型齿轮系统的振动加速度信号。
3.2 仿真模型的试验验证
不同故障状态齿轮系统垂向振动加速度如图14 所示。试验中,由于电机实际转速与预设值之前存在误差,故最终啮合频率frd约为345 Hz,主动轮转频fn1约为16.4 Hz。从图14可以看到:正常齿轮系统在该频段的主要成分仅为啮合频率frd,且没有明显的边频存在;而各故障信号在啮合频率的两侧都有着较为显著的边频存在,且边频之间的间隔为主动轮转频fn1。正常与故障齿轮信号差异显著,但各故障齿轮振动信号之间差异谱图中难以直接识别。上述结果与仿真结果特征一致,证明了所建立动力学模型的正确性。
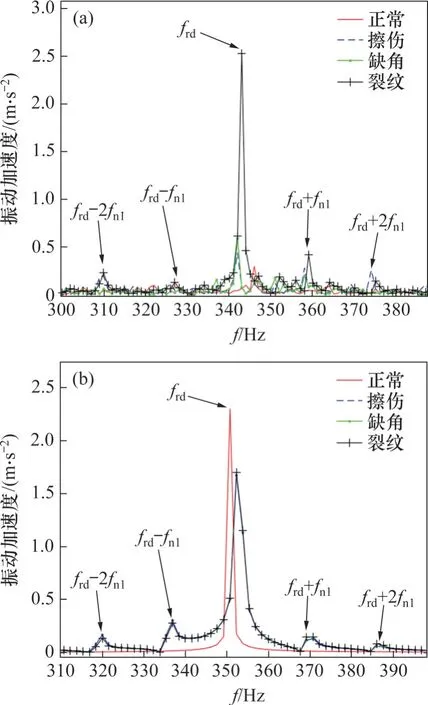
图14 不同故障状态齿轮系统垂向振动加速度频谱Fig. 14 Vertical vibration acceleration of gear system under different fault conditions
3.3 故障诊断方法的试验验证
首先,在4组重复试验中任意选一组作为阈值标定组,以确定波峰计数阈值。通过计算第1组数据在不同阈值下的波峰数来确定有效的阈值范围,如表3 所示。从表3 可知:当阈值ts小于0.12 时,故障齿轮系统信号之间没有明显的差异;当阈值ts大于0.20 时,各齿轮系统通过阈值的波峰数迅速减少。由此可以确定,合理的阈值范围为0.12~0.20。
然后根据确定的阈值范围,选择ts=0.12、0.14、0.16、0.18 和0.20 这5 个阈值,对诊断信号进行截取,统计不同故障类型的波峰数,并计算其平均值,结果如图15 所示。可见不同故障类型的波峰数有显著差异;多组阈值波峰数的平均值排序结果与仿真模型中的故障类型排序结果一致,即裂纹故障波峰数最多,擦伤其次,缺角故障系统振动信号的波峰数最少。试验结果表明,基于波峰计数方法能够对实验室噪声环境和等效转向架结构中不同齿轮故障类型进行准确判别。
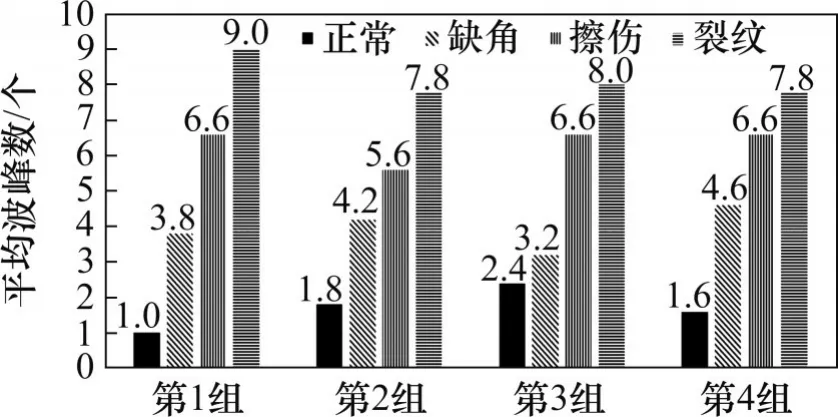
图15 波峰计数诊断方法的试验验证Fig. 15 Experimental verification of peak count diagnosis method
4 结论
1) 考虑弯曲、剪切、接触、径向压缩四方面的力学效应,建立了齿轮擦伤、裂纹、缺角、正常4种状态的啮合刚度模型,并构建了齿轮副啮合的横向振动-扭转振动耦合多自由度动力学模型,为齿轮故障特征研究和故障诊断方法构建提供了重要途径。
2) 基于不同故障类型对啮合刚度的影响差异及导致的振动响应频带分布规律差异,以振动响应中啮合频率附近的频带作为诊断信号,提出波峰计数的故障量化分类方法,通过统计一定阈值范围内多个阈值下的波峰计数平均值,实现了故障类型的量化判别。
3) 转向架齿轮箱故障验证实验所获取振动响应的频谱特征与动力学模型的频谱特征一致,试验与模型所得不同类型故障的波峰计数排列顺序一致,验证了动力学模型的准确性。
