变刚度四足机器人的连续型仿生脊柱设计
2023-10-13钱伟王志瑞苏波党睿娜廖峻北刘思宇郭朝
钱伟,王志瑞,苏波,党睿娜,廖峻北,刘思宇,郭朝
(1. 武汉大学 动力与机械学院,湖北 武汉,430072;2. 中兵智能创新研究院有限公司,北京,100072)
四足机器人具有较好的越障能力,得到了广泛关注[1]。目前,四足机器人仍然存在复杂环境的适应性较差和移动速度较低等不足,比如面向边境巡逻、山地运输、侦察、救援等特殊任务时,四足机器人的应用面临较大挑战[2-3]。为提高四足机器人灵活性及复杂广域地形环境的适应能力,国内外研究者重点研究了腿部机构设计以及步态稳定控制算法[4]。如波士顿动力公司研制的液压驱动四足机器人Big Dog,具有很好的越野性能、负重能力及续航能力[5-6],该公司近期推出的Spot Mini是一款纯电驱动四足机器人,通过与机械臂、深度相机等结合,能够实现搬运物体、爬楼梯等功能[7];MIT 团队设计的Mini Cheetah 四足机器人最快能以2.45 m/s 的速度前行[8]。浙江大学研制的“绝影”四足机器人的质量为70 kg,最大负载为20 kg,最快行走速度可达6 km/h,具有良好的运行性能和弹跳能力,垂直弹跳能力达0.7 m[9];柏龙等[10]设计了一款基于切比雪夫机构和五连杆机构的四足机器人,满足机器人在不同路况下的使用需求。但这些四足机器人采用刚性结构作为整机支撑,降低了四足机器人在复杂环境下的步态稳定性以及在高速奔跑下和快速转向时的被动抗冲击能力。
生物学家在对四足生物运动过程的研究中发现,脊柱能够提高四足生物在高速运动中的稳定性并能起到储能和传递能量的作用。 如HILDEBRAND[11]在观察多种四足生物后,发现猎豹在高速奔跑过程中,充分利用了脊柱伸展和弯曲产生的身长变化来增加步长,从而有效提高奔跑速度,HILBERT[12]发现猎豹的脊柱在奔跑过程中不是固定刚度的,而是具有适应不同速度的变刚度特性。同样,在面对非结构环境时,四足机器人采用柔性脊柱辅助可以有效保持在高速运动以及转身过程中整机的稳定性;通过折叠伸缩柔性脊柱,可以加大四足机器人前后腿的步幅,在相同步频条件下提高四足机器人的运动速度;同时,脊柱的柔性可以在高速奔跑或快速转向的过程中吸收冲击。
目前,国内外许多学者开始研究脊柱结构在四足机器人中的作用,如美国MIT 机器人仿生实验室设计了Cheetah仿生四足机器人,通过差速器使机器人的脊柱在运动时呈现不同状态,达到了较高的运动速度和能量利用效率[13];KHORAMSHAHI 等[14-15]设计了具有单关节脊柱的四足机器人Bobcat,该机器人的脊柱为由电机驱动旋转关节构成,用来连接机器人躯干的前后两部分,并且可在水平面上下35°内实现偏转,增大了步幅和提高了运动速度,并且可以提高飞行相的时间;王琪等[16]为了探索脊柱运动对腿运动的增强机理,设计了具有2自由度铰接式躯干的仿猎豹四足奔跑机器人,实验发现脊柱刚度对机器人运动效果具有调节作用;雷静桃等[17]基于气动人工肌肉设计了一款刚柔耦合脊柱机体,机体最大弯曲角度可达35°,满足四足机器人动态转向需求。这些搭载柔性脊柱的四足机器人主要针对减少能耗以及改善机体运动性能而设计,在小负载条件下进行了仿真或样机测试。但是,当面对大负载、高速奔跑的应用需求时,四足机器人前后腿自重对脊柱产生的转矩以及高速奔跑时受到的冲击力不容忽视,因此,四足机器人的脊柱设计需要有刚柔耦合的动态特性[18-19],以及主动调整刚度的能力,以提高四足机器人环境适应能力和动态特性。
为解决上述问题,本文作者提出一种适用于四足机器人的大负载连续型刚柔耦合仿生脊柱,基于连续型铰接式结构模型,使其能承受大负载的应用需求;对仿生脊柱进行运动学及静力学建模,建立了钢丝绳位移、载荷与脊柱弯曲角度的对应关系;最后,采用阻抗控制算法对脊柱进行变刚度调控实验测试,建立了负载与脊柱响应频率之间的关系,为后续四足机器人的复杂环境应用实验提供前期测试基础。
1 仿生脊柱结构设计
1.1 脊柱仿生机理
KAMIMURA等[20]发现猎豹有两种独特的步态有助于猎豹奔跑,如图1所示。将四肢聚拢在身体下方的聚集飞行和将四肢尽量伸直的延展飞行能够使猎豹在不同条件的地面提供足够的反作用力。而在这两种步态中,脊柱在矢状面上交替进行弯曲和伸展动作,在高速运动中起重要作用。此外,在高速奔跑的过程中,四足生物的脊柱受到支撑四肢运动的转矩以及地面的反作用力矩,使得它受到的轴向载荷远大于人类脊柱所承受的轴向载荷。GALBUSERA 等[21-22]发现四足动物的脊柱骨密度是人类的2~4倍,这表明四足动物的脊柱将受到更高的轴向应力,HUDSON 等[23]分析了猎豹后肢解剖结构,认为脊柱肌肉群对其加速性能和运动能力起到重要作用。
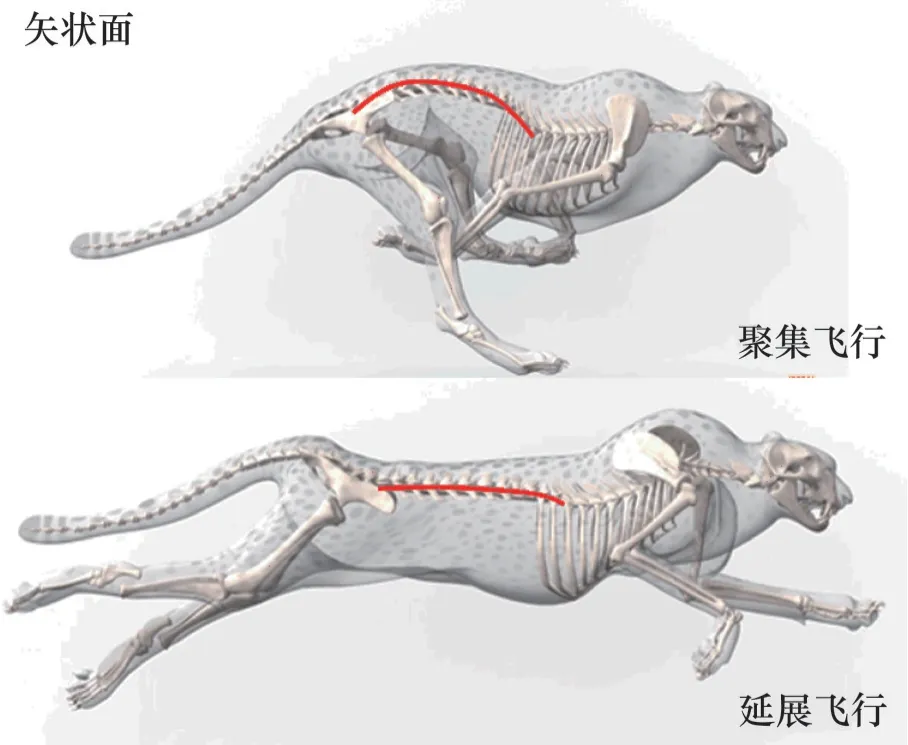
图1 猎豹的两种步态Fig.1 Two gaits of cheetah
根据以上猎豹脊柱的生理特性,本文设计一种在矢状面上弯曲的仿生脊柱,使用金属零件作为脊柱的连接部件和支撑,模拟四足生物的骨架,提高机器人的承载能力;使用钢丝绳传动作为主动驱动方式,模拟四足生物肌肉纤维发力;在脊柱板之间安装了刚度不同的弹簧,模拟肌腱储能与释能。采用连续体构型设计仿生脊柱,与离散型脊柱相比,连续型脊柱可以实现整体的弯曲和回复,使得负载施加的力沿脊柱方向分散,减小脊柱的损耗[24],由于其欠驱动属性及柔顺性,适合进行大幅度的柔性弯曲,解决传统四足机器人腰部刚性约束问题。
1.2 脊柱结构设计
仿生脊柱结构如图2所示。仿生脊柱由6个脊柱板组成,首端脊柱板与末端脊柱板分别负责与四足机器人的前、后腿连接,中间脊柱板允许钢丝绳通过,同时限制绳的径向移动。各脊柱板由滚动轴承转动副连接,各转动副沿周向添加了轴向凸起的限位挡块,以限制各段连续体相对转动角度小于5°,从而将脊柱整体的弯曲角度限制在0°~25°范围内。通过2根钢丝绳将电机输出力矩传递至连续体仿生脊柱从而带动整体实现屈伸运动,钢丝绳一端固定在末端脊柱板上,另一端连接到丝杆滑台,并在外面包裹光滑套筒以减小钢丝绳与脊柱板之间的摩擦。

图2 脊柱三维模型图Fig.2 3D model of bionic spine
为了保证脊柱在受到前后两侧腿部产生的弯矩作用后能够维持所期望的初始向上拱起弯曲姿态,在各脊柱板中加入上下两排压缩弹簧,同时使上排压簧的刚度大于下排压簧的刚度,以此增加连续体的静态刚度,并维持脊柱为期望的初始姿态。通电后,在丝杠滑台的作用下,将电机的旋转运动转化为钢丝绳的直线转动,提供的驱动力使得各段连续体恢复至水平状态,以达到控制脊柱屈伸的仿生运动。四足机器人三维模型图如图3 所示,图中四足机器人处于脊柱拉直至水平状态。

图3 四足机器人三维模型图Fig.3 3D model of the quadruped robot
1.3 弹簧设计及电机选型
连续型仿生脊柱全长为236 mm,总质量为6.2 kg,每节脊柱板为厚6 mm 的碳板,在拉直状态下,2块脊柱板的间距为40 mm。四足机器人的前后腿质量均为30 kg,为提供初始推力且防止失稳,需设计刚度及长度适宜的上下排弹簧。
四足机器人腿部受力分析如图4 所示,图中,G1为后腿质量,G2为脊柱质量,F为脊柱施加在后腿上的竖直方向分力,τ为脊柱给腿部水平方向分力与地面给支点N的摩擦力合成的等效力矩;L1和L2分别为脊柱作用点到腿部重心的横向距离和足底作用点到腿部重心的横向距离。为便于计算,设前后腿成对称布置,则有
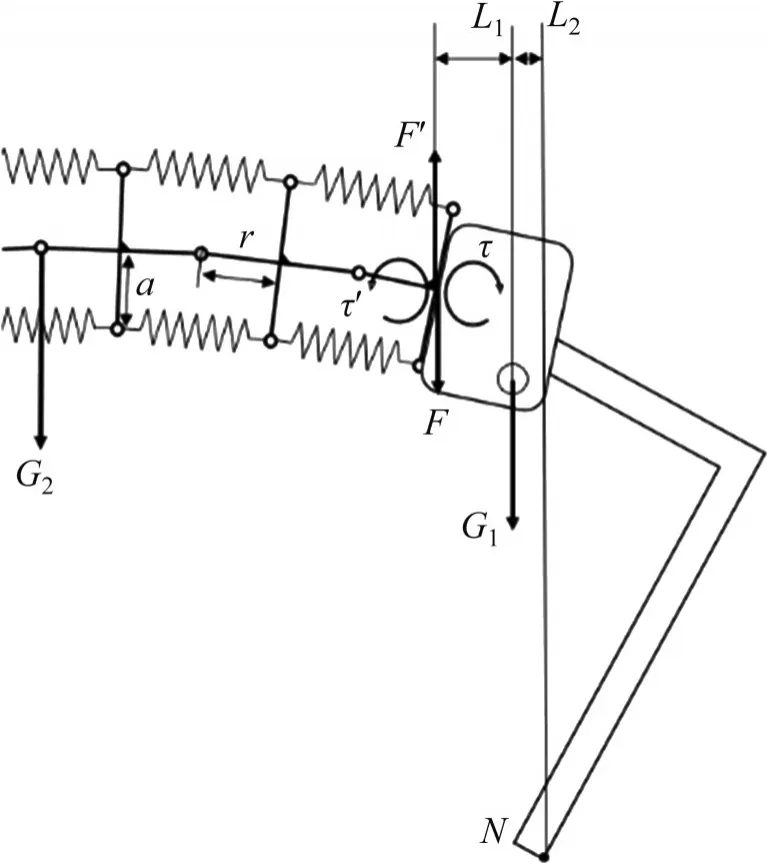
图4 四足机器人腿部受力分析Fig. 4 Force analysis of the leg of the quadruped robot
代入数值计算得到τ为7.8 N·m,而上下排弹簧施加在末端脊柱板上的力矩τ0为
其中:Δx1和Δx2分别为大刚度和小刚度弹簧的形变量,其刚度系数分别为k1和k2;a为脊柱板中心到弹簧中心轴距离;r为每一节铰接转动轴离脊柱板的连杆长度;θ为每一节铰接转动轴偏转的角度。
为了保证在连接上四足机器人的前后腿后,承受反向弯矩时也能呈现25°初始弯曲角度,需要令τ0>τ,设置上排弹簧长度为55 mm,刚度为13.88 N/mm,下排弹簧长度为45 mm,刚度为2.38 N/mm。选择KK50 精密丝杆滑台作为脊柱的传动件,其行程为50 mm,丝杆导程为2 mm。在计算钢丝绳最大受力情况后,选择驱动电机为Maxon EC90 Flat,其额定输出力矩为0.933 N·m,堵转力矩为7.47 N·m。在分析计算上下弹簧推力差以及拉绳和负载的力臂后可得到电机额定输出力矩,此时,仿生脊柱的最大负载为334.9 N。
2 仿生脊柱静力学分析
在一般的连续型机器人弯曲过程中,机器人脊柱板和支架的质量可以忽略不计,可以将机器人各关节假定为弯曲曲率相等的光滑连续曲线,即常曲率假设模型[25-26],但本设计中的刚柔耦合机构需要在大负载条件下运行,其质量不可忽略[27],脊柱板之间角度变化不相同,因此需要建立静力学模型以确定在钢丝绳拉力及负载的共同作用下每一个脊柱板之间的角度[28-29]。在大负载四足机器人的工作场景中,脊柱通常是匀速运动或速度变化缓慢,因此不考虑动力学特性[30]。
图5所示为仿生脊柱的侧面受力分析图,以脊柱前端,即前腿与脊柱连接处为原点建立笛卡尔坐标系,脊柱末端点记为S,b为脊柱板厚度,脊柱板之间的角度从前端到后端分别为θ1、θ2、θ3、θ4和θ5。假设四足机器人前腿固定,后腿相对于前腿运动,等效于对脊柱S点施加外载荷F,对最末端一节脊柱板进行受力分析,如虚线框中部分所示,末端脊柱板上受到大刚度弹簧的推力F1、小刚度弹簧的推力F2和钢丝绳的拉力T,由于钢丝绳外设有光滑套筒,与脊柱板之间的摩擦因数较小,钢丝绳与脊柱板之间的摩擦与钢丝绳的拉力相比很小,为简化计算忽略摩擦力的影响。每个脊柱板的质量相同,质心位置在截面图上与S点重合,由于转动轴和脊柱板之间的连杆质量以及弹簧的质量相比脊柱板质量很小,且沿脊柱板两侧成对称布置,故将其质量等效至S点处,合记为M。对末端转动轴中心列力矩平衡方程可得:
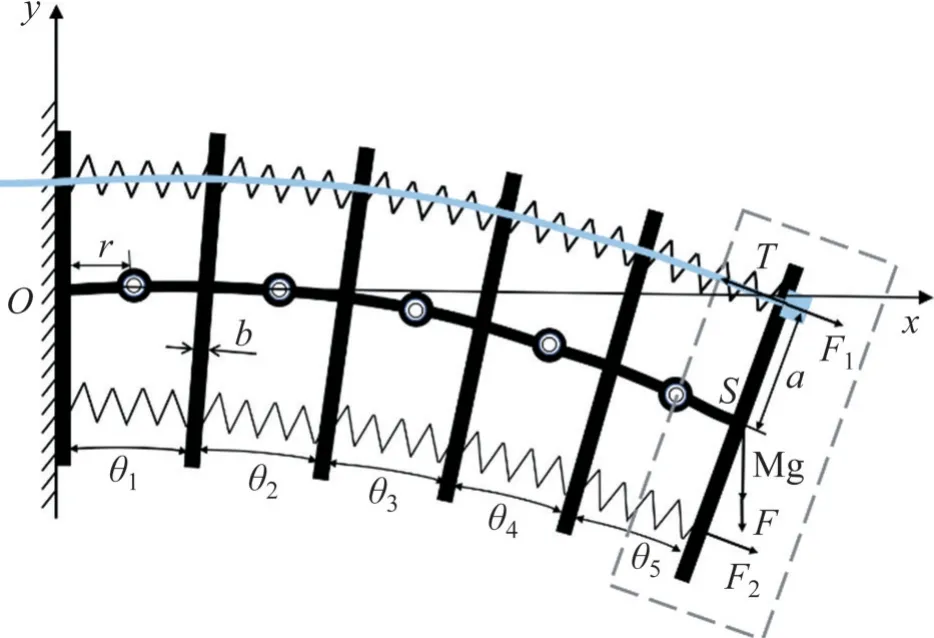
图5 仿生脊柱受力分析Fig. 5 Force analysis of the bionic spine
式中,∆x1,5和∆x2,5分别为第五节大刚度和小刚度弹簧的形变量。
考虑到每一节脊柱板之间的角度变化很小,最大为5°,因此sinθ可近似为θ,则
同理可得第i节的脊柱板受力情况,从而得到对转动轴中心的力矩平衡方程通式:
式中:m=-a2(k1+k2);n=-2r-b;P、Q和C分别为速度矩阵、角度矩阵和力矩矩阵的系数。
在给定绳拉力T和负载F的情况下,通过数值迭代方法求解式(6),可得每个脊柱板之间的角度,从而可以求得脊柱末端点S点纵坐标yS为
脊柱的等效整体弯曲刚度Kd定义为
3 仿生脊柱性能仿真与实验测试
四足机器人整体图如图6所示。本文设计的脊柱与四足机器人前后腿完成装配,并进行脊柱弯曲实验,如图7所示,实验结果表明,本文设计的脊柱满足四足机器人使用需求。

图6 四足机器人整体图Fig. 6 Overall view of the quadruped robot

图7 四足机器人弯曲实验Fig.7 Bending experiments of the quadruped robot
为验证连续型脊柱模型的准确性及测试脊柱运动性能,搭建了如图8 所示的实验平台,其中,在末端脊柱板处加设2 个挂钩,以方便增加负载;在每一块脊柱板上加装一个惯性测量单元(IMU),以获得各节脊柱转角,在2根钢丝绳的末端加装环形压力传感器,以获得钢丝绳上的总拉力。

图8 脊柱性能测试实验平台Fig. 8 Experimental platform of spine performance test
在理论计算中,由于无法直接获得脊柱各节转角的解析表达式,为确定绳子拉力以及末端负载对脊柱各节转角的影响,根据上节所建立的力学模型进行模拟计算,其中,将钢丝绳上的拉力T以及末端挂的负载F设为自变量,θ1~θ5设为因变量,利用数值迭代方法进行仿真实验,作为样机实验的对比。
3.1 变力恒载实验
为模拟运动过程中四足机器人后腿离地,仅前腿支撑时的状态,将负载设定为0 kg 和30 kg,其中,30 kg 为四足机器人后腿的质量。在理论计算中,分别将负载F设为0 N和300 N,改变拉力T进行迭代计算;在实验平台上,分别进行空载以及30 kg 负载实验,根据IMU 测得的θ1~θ5以及连杆长度r绘制出脊柱侧视图,其中起始的圆圈表示前腿与脊柱板的连接点,即图5中的O点,末端的圆圈表示后腿与脊柱板的连接点,即图5 中的S点,中间的圆圈表示转动副;按实验时间等间隔选取5 个特征点处的拉力0、742.0、1 040.4、1 383.2 和1 444.0 N。变力恒载实验结果与理论计算结果如图9所示。
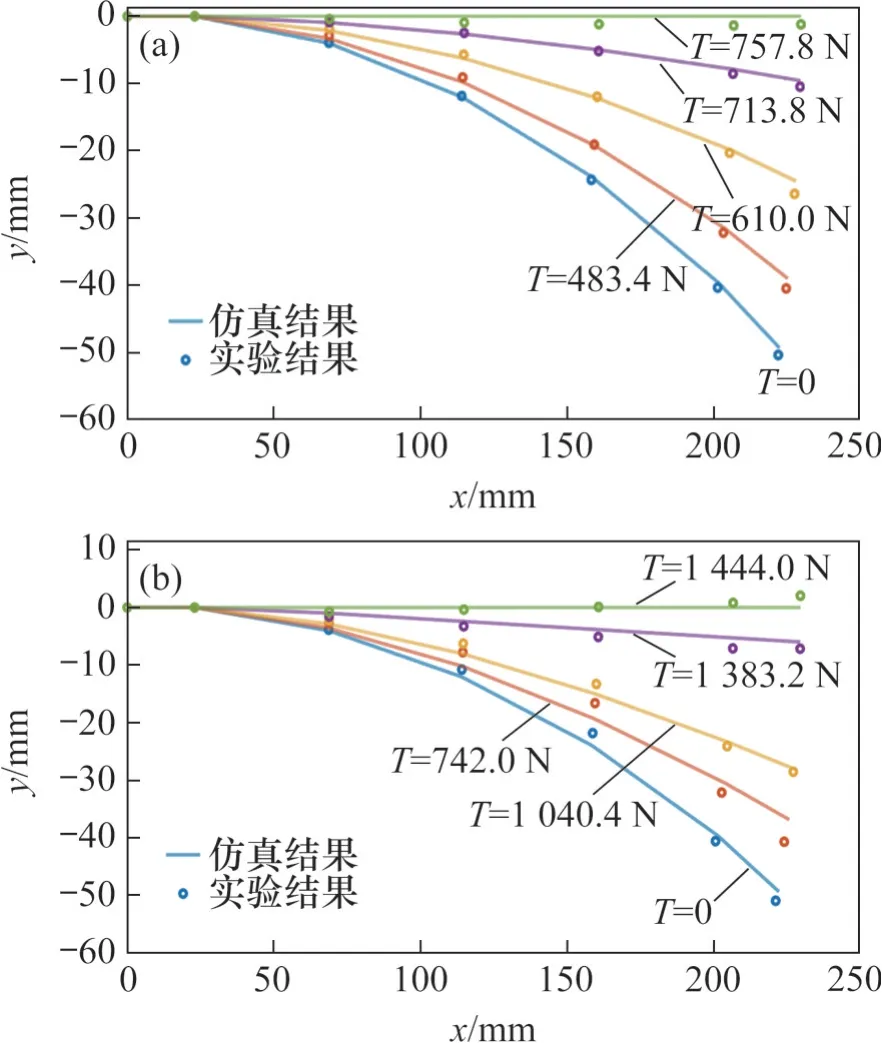
图9 变力恒载实验结果Fig. 9 Experimental results of variable force and constant load
连续型结构每一节的实验与理论计算的误差会累积,故采用最末端点的位置误差来体现模型与实际结果之间的差距。每节选取5个特征点位置计算平均误差及相对误差,结果如表1所示。
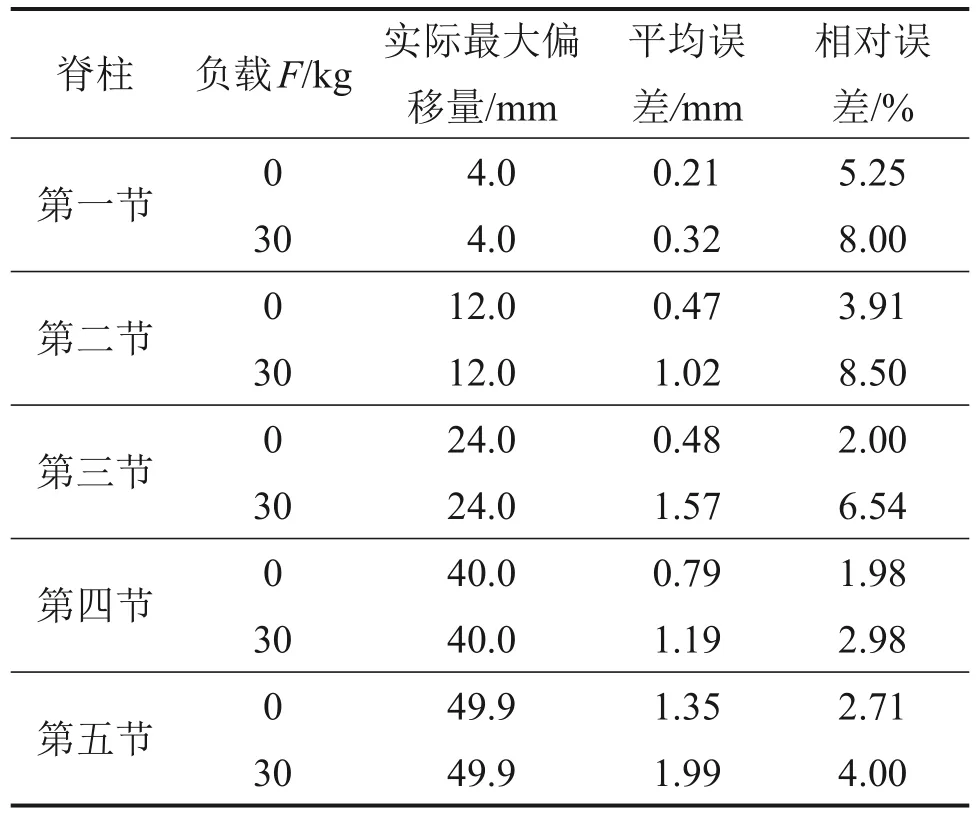
表1 变力恒载实验各节端点位置实际值与理论值误差对比Table 1 Comparison of error between actual and theoretical values at each endpoint position under variable force constant load
从图9 可以看出,在末端负载较小的情况下,随着拉力的提升,首先是最接近前腿的一节脊柱板拉直至限位处,再依次往后各个脊柱板拉直至限位处;在末端负载较大的情况下,随着拉力的提升,首先是最远离前腿的一节脊柱板拉直至限位处,再依次往前达到限位。从表1可见:实际与理论计算值相对误差较小,说明所建立的力学模型有效。
3.2 恒力变载实验
根据3.1 节的实验结果,选取拉力T分别为750 N 和1 400 N 作为定拉力进行恒力变载实验,负载分别取0、5、10、15和20 kg。理论计算与实验对比结果如图10 所示。每节5 个特征点位置的平均误差及相对误差如表2所示。
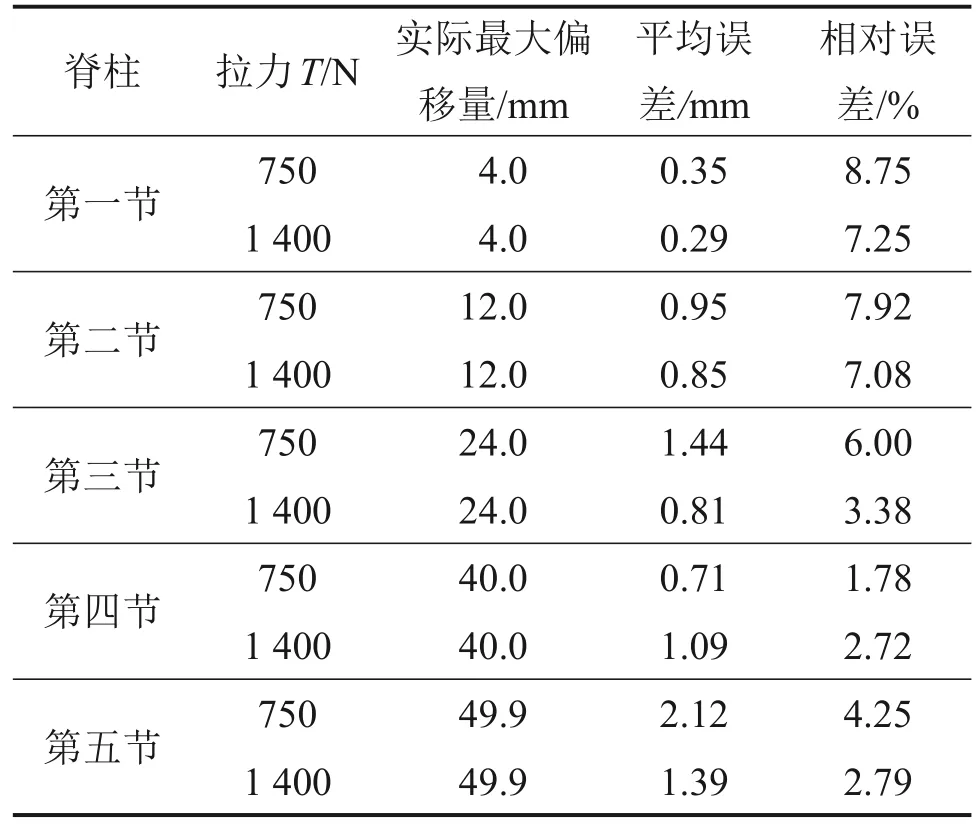
表2 恒力变载实验各节端点位置实际值与理论值误差对比Table 2 Comparison of error between actual and theoretical valuses each endpoint position under constant force variable load
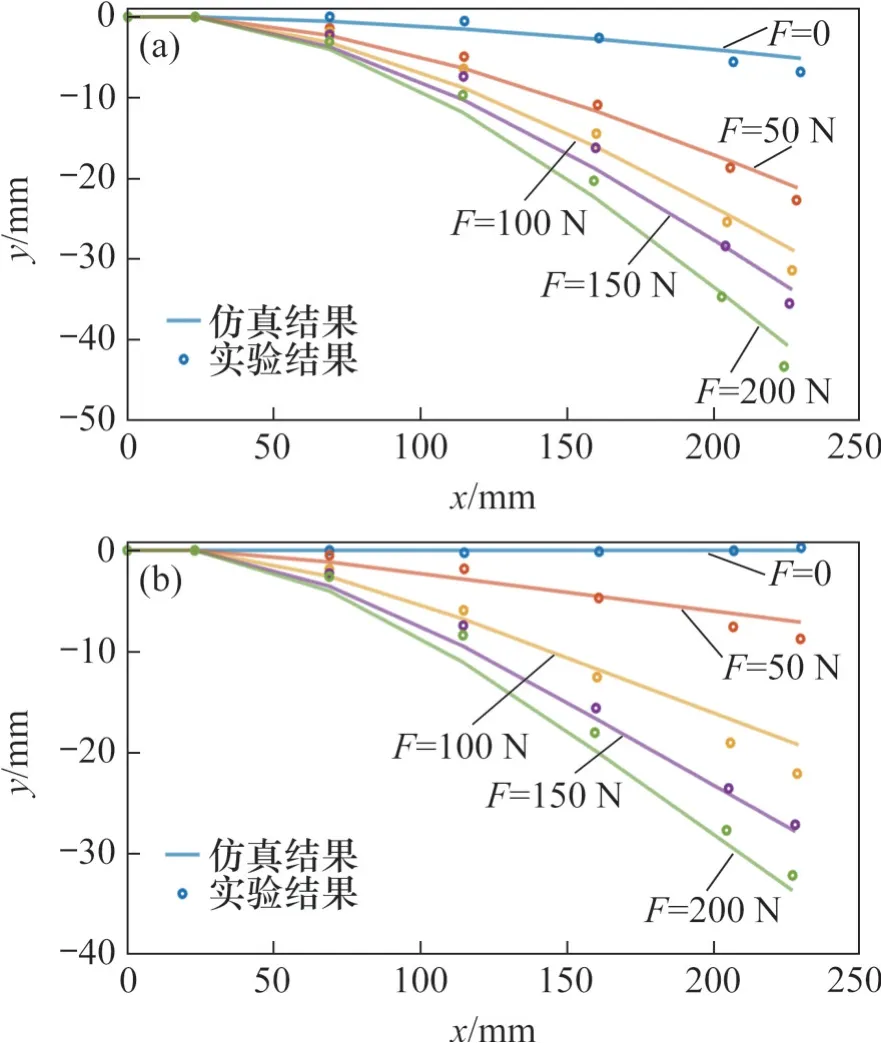
图10 恒力变载实验结果Fig. 10 Experimental results of constant force and variable load
由图10 可知:在拉力较小、负载较大的情况下,最接近前腿的一节脊柱板先发生形变并先达到限位;在拉力较大、负载较小的情况下,最远离前腿的一节脊柱板先发生形变并先达到限位。结合上述实验结果可以看出,本文所提出的理论计算模型与实际结果的相对误差不超过5%。
3.3 频率响应实验
为保证在后续与四足机器人腿足协调控制中,能配合腿部机构进行伸展和弯曲动作,负载为30 kg进行频率响应实验,实验结果如图11所示,图中,脊柱末端位置定义与图5中一致,表示末端位置偏离水平位置的距离,为防止频率过快对限位造成冲击较大,选取末端运动范围为-5~-48 mm,对应钢丝绳移动范围为28 mm。通过多次实验计算得到在相对误差不超过5%的情况下,跟踪曲线的最大频率为1.62 Hz,满足腿足协同控制中的频率需求。
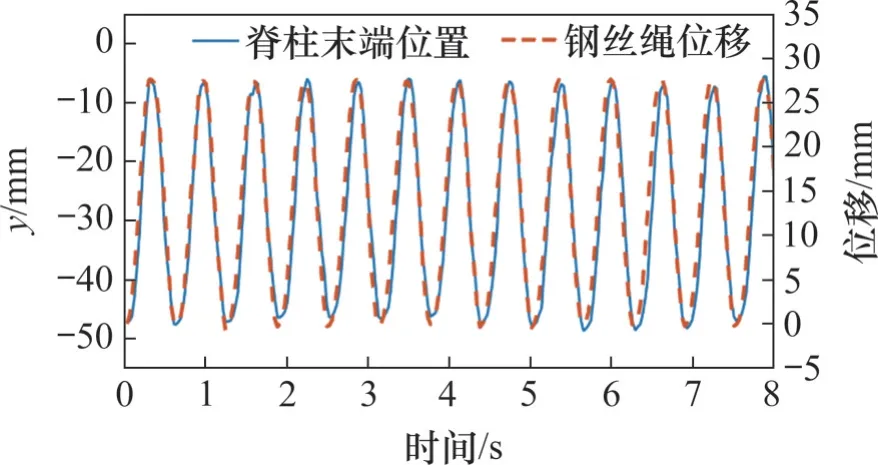
图11 频率响应实验结果Fig.11 Experiment result of frequency response
3.4 变刚度控制实验
四足生物在运动时利用脊柱的柔性以获得更好的运动稳定性、运动速度及能量效率。为实现四足机器人在面对非结构环境下的柔性控制,使用阻抗控制算法生成虚拟刚度以配合生物腿的关节刚度随运动速度的变化和地面接触刚度的实时变化,模拟四足生物脊柱的主动柔性。本实验中,以水平位置作为期望位置,设置不同虚拟刚度(K=0.50、0.20、0.10、0.05),并加10 kg负载,记录各个IMU 的结果并绘制脊柱侧视图,实验结果如图12 所示,图中,由于脊柱结构自身重力作用,使得脊柱初始情况下不是水平状态。
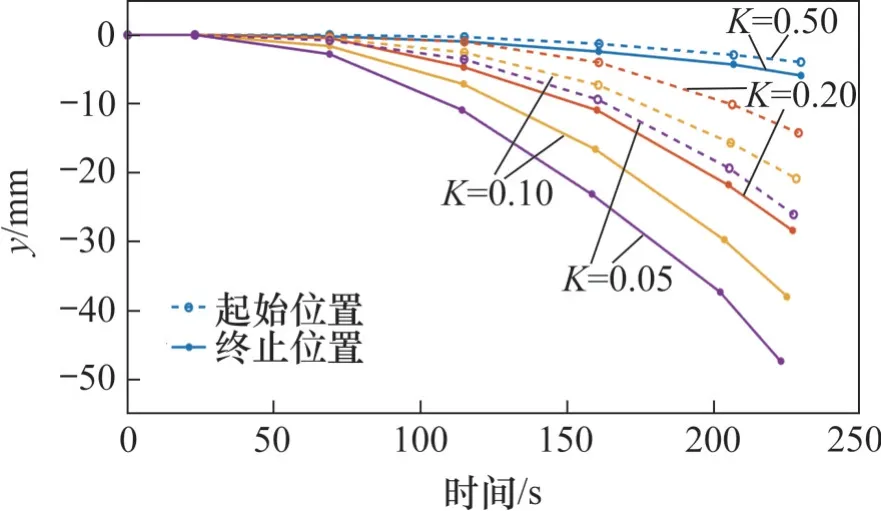
图12 变刚度控制实验结果Fig.12 Experiment of variable stiffness control
根据脊柱的等效整体弯曲刚度Kd的定义,计算不同虚拟刚度系数下Kd,结果如表3所示。从表3可见,通过阻抗控制可以调节脊柱的等效弯曲刚度Kd从4.70 N/mm 增加至51.36 N/mm,可以适用于后续的机器人样机控制实验。
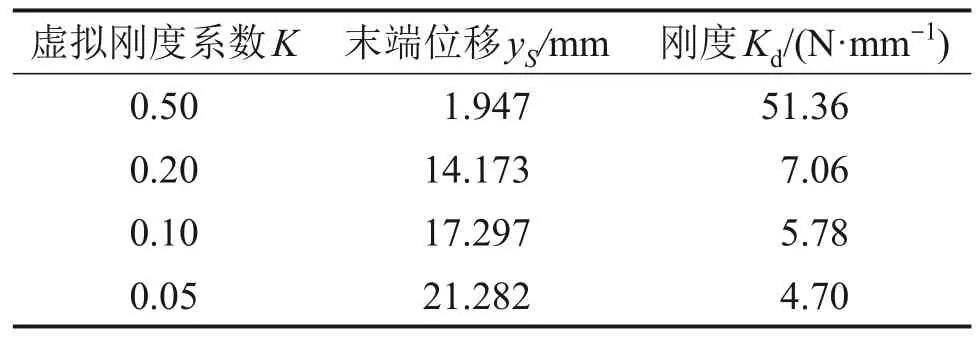
表3 不同虚拟刚度下脊柱末端位移与刚度Table 3 Distal spine displacement and stiffness under different virtual stiffness
4 结论与展望
1) 根据四足生物的脊柱运动特征设计了一种在矢状面上可以连续弯曲的刚柔耦合连续体仿生脊柱,利用其欠驱动属性及柔顺性,使四足机器人腰部可以进行大幅度的柔性摆动,解决传统四足机器人腰部刚性约束的柔顺性不足。
2) 根据结构设计及工作情况建立了脊柱的静力学模型,利用理论计算和实验验证了模型的准确性,并进行频率跟踪及变刚度控制实验验证所设计仿生脊柱的可行性,实现了大范围变刚度输出,有助于提高四足机器人复杂环境的地形适应性。
3) 本文设计的连续型仿生脊柱已安装于四足机器人上,为了更好地提升四足机器人的运动性能,在之后的工作中,将对柔性脊柱与腿部协同运动控制算法进行研究。
