基于滑动窗邻域保留投影的工作模态分析
2023-10-12符伟华陈建伟
符伟华,王 成,2+,陈建伟
(1.华侨大学 计算机科学与技术学院,福建 厦门 361021;2.西安交通大学 机械结构强度与振动国家重点实验室,陕西 西安 710049;3.圣地亚哥州立大学 数学与统计学院,圣地亚哥加州 美国 92182)
0 引言
工作模态分析可仅利用结构输出的振动位移响应信号识别结构的工作模态参数(模态振型、固有频率和阻尼比)[1],进而应用于结构损伤检测[2]、结构设计[3]等。
流形学习[4](manifold learning)从首次被提出至今都是计算机研究热点之一。流形学习的目的是找到数据在高维空间中的低维嵌入和相应的嵌入映射[5]。常见的流形学习算法有主成分分析(Principal Component Analysis,PCA)[6]、等距离映射(Isomap)[7]、局部线性嵌入(Locally-Linear Embedding,LLE)算法[8]等。
目前,为识别时不变结构的工作模态参数,王成等[9-10]提出利用PCA和Isomap算法识别结构的工作模态参数。白俊卿等[11]利用LLE算法识别出复杂三维连续体结构的工作模态参数。符伟华等[12-13]利用拉普拉斯特征映射(Laplacian Eigenmaps,LE)和邻域保留投影(Neighborhood Preserving Embedding,NPE)算法识别结构的工作模态参数。但现实中,大多数结构具有时变的特性[14],故结构的工作模态参数也具有时变特性。当前,针对线性慢时变结构的工作模态参数识别问题,主要有时域法和频域法。ZHOU等[15]详细分析并总结了这些方法的优缺点。线性慢时变结构的振动响应信号往往无法一次性完整获取,需要通过随着时间的推移,不断进行采样得到。因此,基于“短时时不变”理论的滑动窗方法能很好应用于线性慢时变结构工作模态参数识别中。目前,滑动窗方法已应用在一些算法上做线性慢时变结构的工作模态参数识别。官威等[16-17]将滑动窗与主元分析相结合,有效地识别了多自由度系统的工作模态参数。黄海阳等[18]提出了基于滑动窗变步长等变自适应源分离(Equivariant Adaptive Separation via Independence,EASI)算法识别了线性慢时变系统的工作模态参数。
为提高线性慢时变结构工作模态参数的识别精度,本文提出将滑动窗技术(Moving Window,MW)[19]与NPE算法[20]相结合,提出了一种基于MWNPE的线性慢时变结构工作模态参数识别方法。滑动窗技术能追踪慢时变结构的时变特性,NPE算法在降维过程中,能保持原始数据集的局部线性特性,这与工作模态参数的数据内部的特征关系高度相似,从而有效识别线性慢时变结构的工作模态参数(模态振型、固有频率和阻尼比)。
1 相关工作
1.1 线性慢时变工作模态参数识别问题描述
根据结构的动力学理论,在时长为t∈[TBEGIN,TEND]内,n自由度线性慢时变结构在物理坐标系统中的运动方程为:
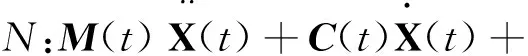
(1)
式中:M(t)∈n×n为慢时变结构的质量矩阵,C(t)∈n×n为慢时变结构的阻尼矩阵,K(t)∈n×n为慢时变结构的刚度矩阵;n×T依次为慢时变结构的位移响应信号、速度响应信号与加速度信号的时域采样矩阵;F(t)∈n×T为慢时变结构的外载荷激励向量的时域采样矩阵。
依据时间冻结理论,线性慢时变的离散多自由度系统在极小的时间段τ∈[tbegin,tend]内,其质量、阻比与刚度可被视为时不变的。因此,式(1)在完整的时长t∈[TBEGIN,TEND]内,可表示为一组由有限个线性时不变结构N′(τ)(τ∈[tbegin,tend])构成的集合N′,
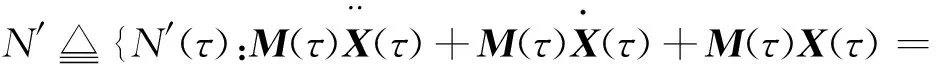
(2)
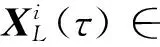
(3)

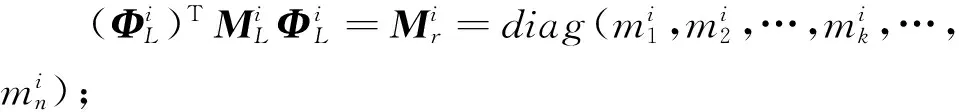
(4)

(5)
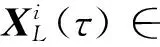
1.2 基于邻域保留投影的工作模态参数识别
X(t)MXT(t)a=λX(t)XT(t)a;
(6)
B≜X(t)ST(t)(S(t)ST(t))-1;
(7)
(8)
在式(6)中,矩阵M为半正定的对称矩阵,NPE算法更为详细的降维过程可参考文献[20]。对比式(3)与式(8)可知,X(t)∈n×L的低维嵌入S(t)与模态响应相对应,转换矩阵B与模态振型相对应。如图1所示为NPE算法与识别工作模态参数的对应关系。
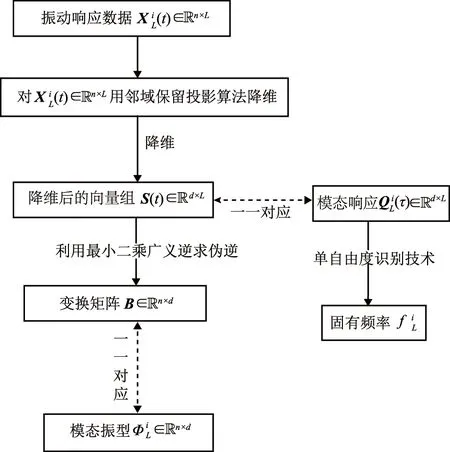
图1 基于NPE算法的工作模态参数识别原理图
1.3 滑动窗口技术
滑动窗口技术(MW)是基于时间冻结理论,将在每个窗口内的非平稳时变信号视为时不变的平稳信号,从而对该窗口(时间段)内的振动响应信号运用识别时不变工作模态参数的方法,识别出该窗口的瞬时工作模态参数。在识别完该窗口的工作模态参数后,固定长的窗口向右移,删除窗口内部分旧数据并增加新的数据项,形成下一窗口(时间段)的振动响应数据,如图2所示为滑动窗口移动的过程。

图2 固定窗长滑动窗口滑动过程
1.4 基于MWNPE算法的线性慢时变结构工作模态参数识别
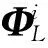
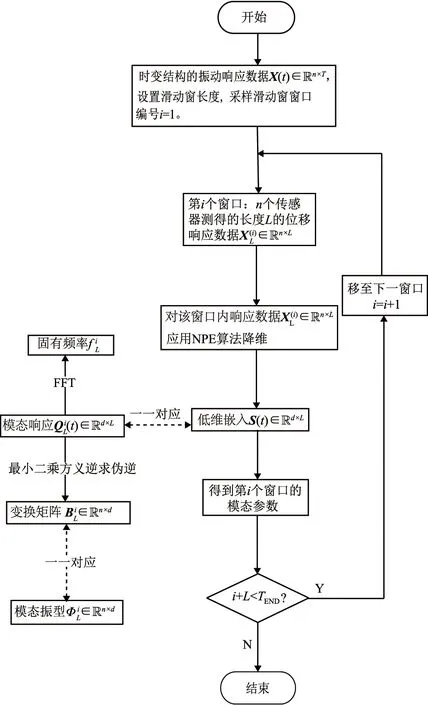
图3 MWNPE识别线性慢时变结构工作模态参数的流程图
1.5 方法的适用范围和理论分析比较
本文提出的基于NPE线性时不变工作模态参数识别适用范围和理论分析比较如下:
(1)振动响应传感器的布置个数要不小于可识别的阶数;
(2)结构的外界激励向量应能视为是平稳的高斯白噪声;
(3)结构是线性慢时变的;
(4)本文主要将基于MWPCA、MWEASI[18]线性慢时变结构的工作模态参数识别方法进行比较。NPE算法相比线性的PCA算法,NPE算法是通过保留数据局部线性特征完成对全局特征的构造,有助于识别出PCA不能识别的非线性特征模态。相比MWEASI方法,MWNPE方法的跟踪时变能力更强,精度更高,且缺失模态现象更少。因此,基于MWPCA、MWEASI与MWNPE三种方法识别线性慢时变结构的工作模态参数的对比如表1所示。

表1 基于MWNPE、MWPCA和MWEASI线性慢时变结构的工作模态参数识别方法比较
1.6 参数设置
在仿真验证中,固定窗口长度L设置为1 024,NPE算法使用的K近邻算法的K=40。
2 仿真验证与结果分析
2.1 仿真对象和数据集介绍
本文通过设计一个线性质量慢时变的三自由度弹簧振子结构对MWNPE算法的有效性进行验证。结构模型如图4所示。
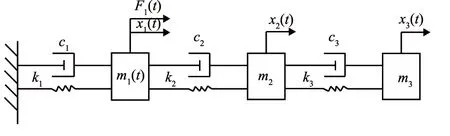
图4 线性质量慢时变的三自由度弹簧振子结构系统激励模拟图
结构动力方程如式(9)所示。结构参数如下:3个物体的阻尼比c1=c2=c3=0.01 N·s/m,刚度k1=k2=k3=1 000 N/m,初始位移皆为0,除此之外,物体的质量m2=m3=1 kg,物体m1的质量是慢时变的,变化规律如式(10)所示。
(9)
(10)
高斯白噪声激励是一种在频域内为平谱的平稳随机激励。对于无阻尼和小阻尼线性时不变结构,通过施加高斯白噪声激励所得到的振动响应主要由结构在各固有频率下的振动响应组成,所得的频率是结构的固有频率[22]。F(t)为高斯白噪声,施加在物体m1上,且因为在前50 s物体m1的质量是恒值,所以前50 s为线性时不变结构。在50 s后,物体m1的质量随时间而变化,结构变为线性慢时变结构。仿真的采样时间间隔为0.025 s,采样频率设置为40 Hz,系统在MATLAB/Simulink的模型设计如图5所示。三自由度的弹簧振子数据集X(t)如图6所示,采样时长为2 000 s,因此最终得到的数据集X(t)∈3×80 001,即n=3,T=80 001。结构的理论固有频率如图7所示。
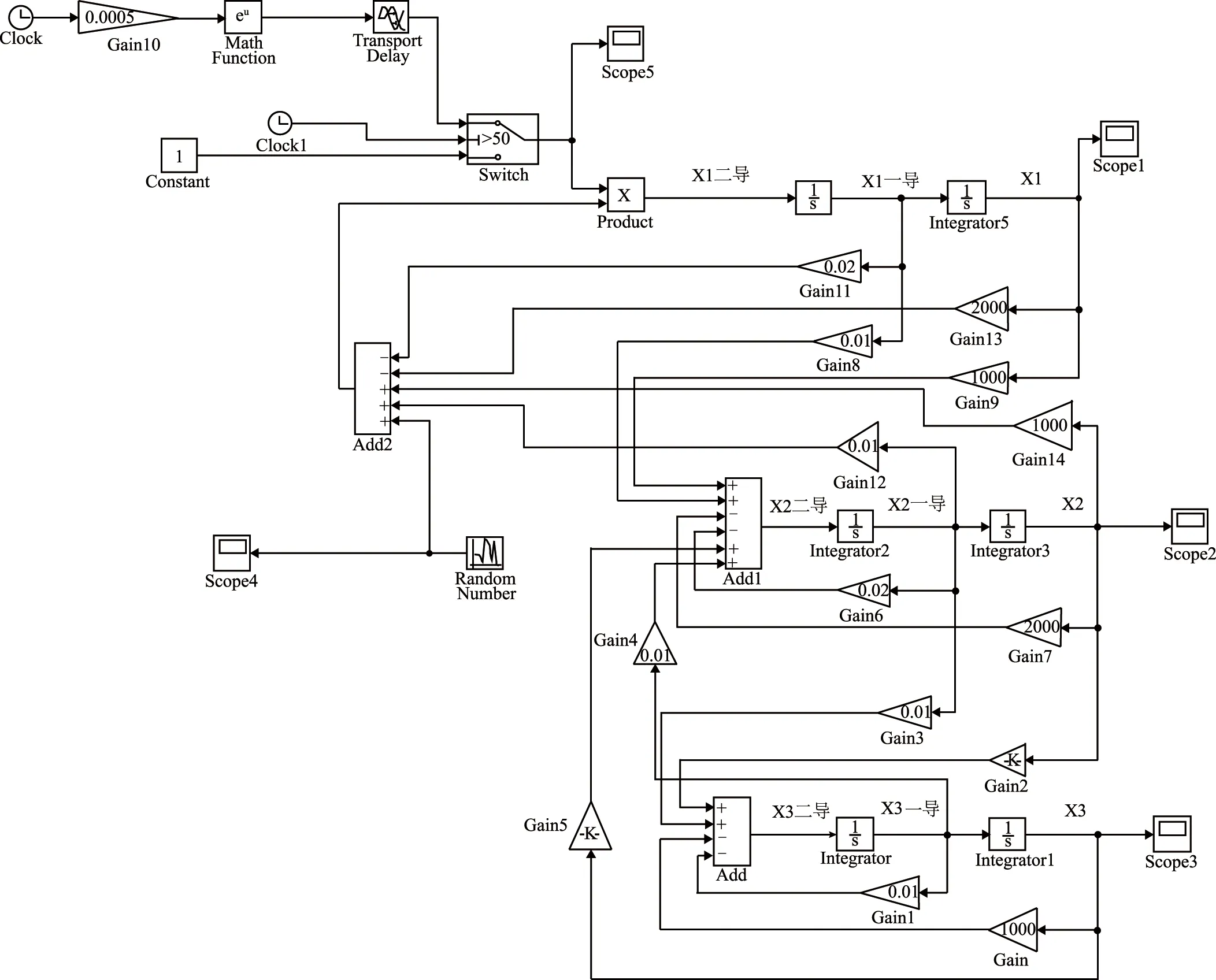
图5 Simulink质量线性慢时变三自由度的弹簧振子系统仿真模型图
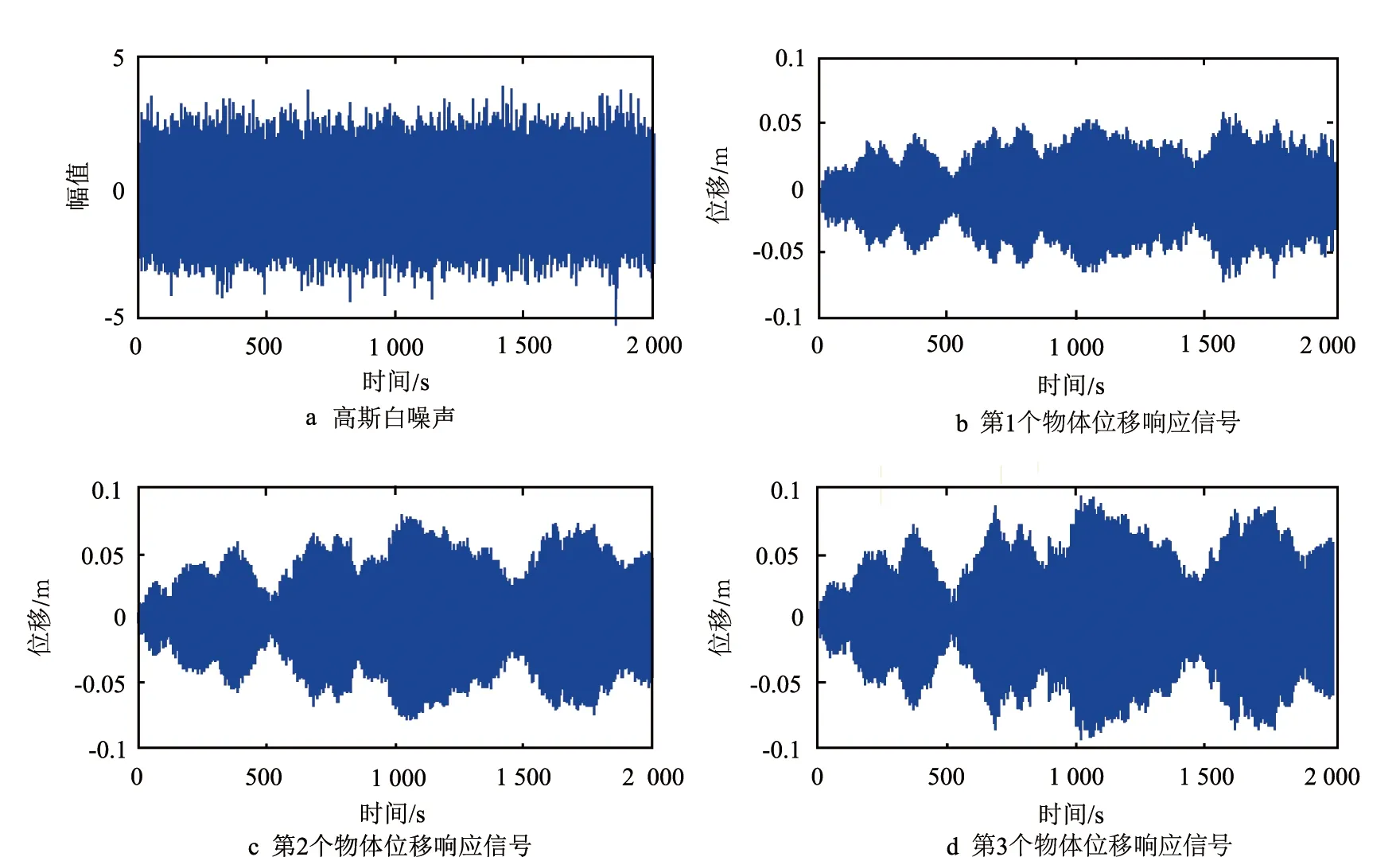
图6 高斯白噪声和3个物体位移响应信号图
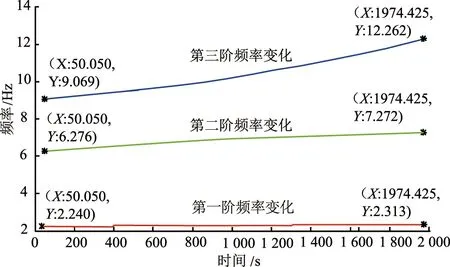
图7 三自由弹簧振子结构的三阶理论固有频率随时间变化图
2.2 评价指标
为评价MWNPE算法识别线性慢时变三自由度(3 Degrees of Freedom,3-DDF)结构模态参数的精度,本文用MWNPE算法识别到的模态参数与有限元方法分析识别到的模态参数作为理论值进行比较。
本文将使用模态置信度准则(Model Assurance Criterion,MACi-avg)来评估MWNPE算法识别到的第i阶模态振型平均准确度[23],MACi-avg的具体定义如下:
(11)
式中:m为窗口总个数,φij是MWNPE算法识别得到的第i阶第j个窗口模态振型,ψij是真实的第i阶第j个窗口模态振型。由式(11)可知模态置信度准则的取值范围是0≤MACi-avg≤1,当MACi-avg的值越接近1时,说明MWNPE识别第i阶的模态振型精度越高。
误差率(δi-avg)将用于评价识别第i阶固有频率的平均准确性,
(12)
式中:m为窗口总个数,fij为MWNPE算法识别得到的第i阶第j个窗口固有频率,fij-理论为真实的第i阶第j个窗口固有频率。由式(12)可知,当δi-avg的值越接近0时,说明MWNPE识别第i阶的固有频率精度越高。
2.3 工作模态参数识别结果
在线性慢时变结构中,结构的工作模态参数随时变化。在质量慢时变三自由度结构(3-DOF)中,本文选取了t=100 s、t=650 s、t=1 650 s、t=1 974.375 s四个时刻进行描述。如表2所示为4个时刻的瞬时MAC值,如图8所示为4个时刻的模态振型与理论值比较图。如图9所示为MWNPE算法识别的三阶固有频率变化图。如图10所示为MWNPE识别的三阶模态振型的MACi-avg值变化图。在结构工作模态参数辨识过程中,部分窗(时刻)的模态参数未能识别,如表3所示为MWNPE、MWEASI和MWPCA之间未识别窗口的数量。如表4所示为MWNPE、MWEASI和MWPCA识别的模态振型置信度值MACi-avg。

表2 质量慢时变3-DOF结构中t=100 s、t=650 s、t=1 650 s、t= 1 974.375 s四个时刻的MAC值
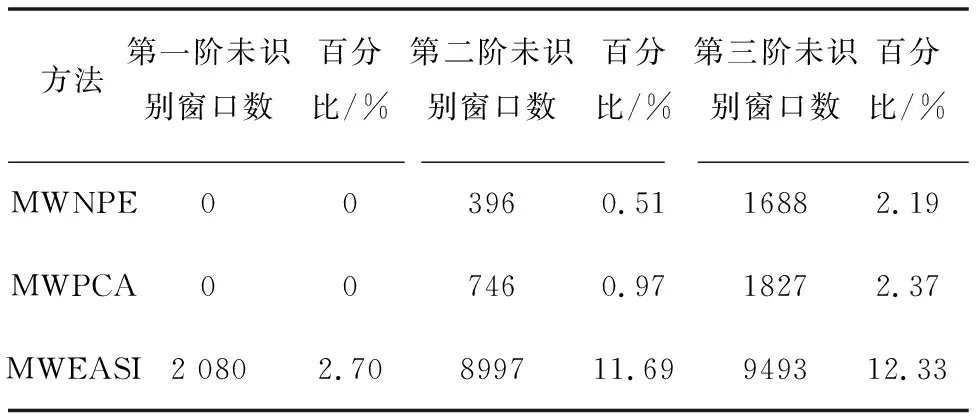
表3 MWNPE、MWPCA和MWEASI未识别质量慢时变3-DOF结构的窗口数量

表4 MWNPE、MWPCA和MWEASI识别质量慢时变3-DOF结构的模态振型MACi-avg比较

图8 MWNPE识别质量慢时变3-DOF结构(t=100 s、t=650 s、t=1 650 s和t= 1 974.375 s)的模态振型

图9 MWNPE算法识别的三阶固有频率变化图
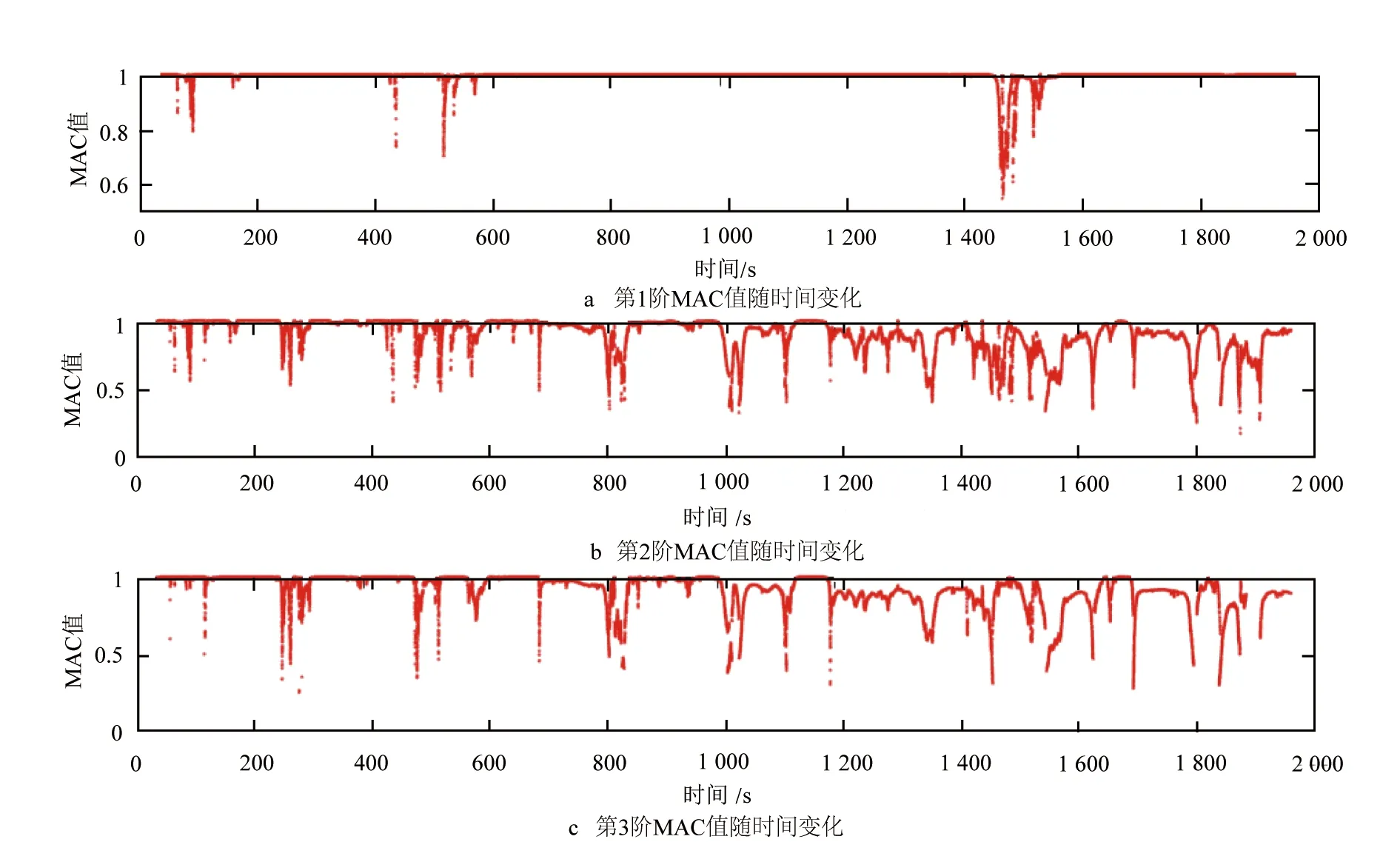
图10 MWNPE识别的三阶模态振型的MACi-avg值变化图
为进一步验证MWNPE算法的识别线性慢时变结构的有效性,本文在线性三自由度结构的振动位移响应信号中加入10%的高斯白噪声,再识别结构的工作模态参数。在含有10%高斯白噪声的质量慢时变三自由度结构中,同样选取了t=100 s、t=650 s、t=1 650 s、t=1 974.375 s四个时刻进行描述。表5给出了这4个时刻的瞬时MAC值。如图11所示为MWNPE算法识别的三阶固有频率变化图。如图12所示为MWNPE识别的三阶模态振型的MACi-avg值变化图。如表6所示为MWNPE识别加入10%高斯白噪声结构的固有频率平均误差。在结构工作模态参数辨识过程中,如表7所示为MWNPE识别加入10%高斯白噪声结构的未识别窗口数量。如表8所示为MWNPE识别加入10%高斯白噪声结构的模态振型置信度值MACi-avg。

表5 带10%高斯白噪声的慢时变3-DOF结构中t=100 s、t=650 s、t=1 650 s、t= 1 974.375 s四个时刻的MAC值
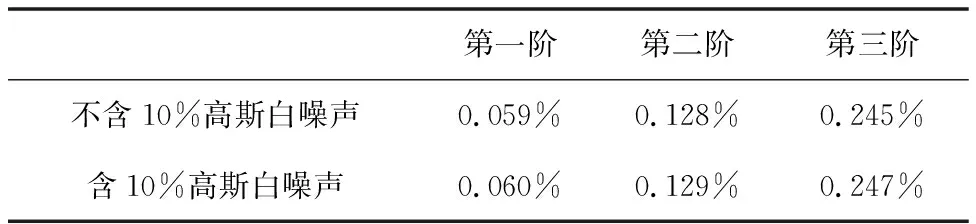
表6 MWNPE质量慢时变3-DOF结构的固有频率平均误差

表7 MWNPE未识别质量慢时变3-DOF结构的窗口数量
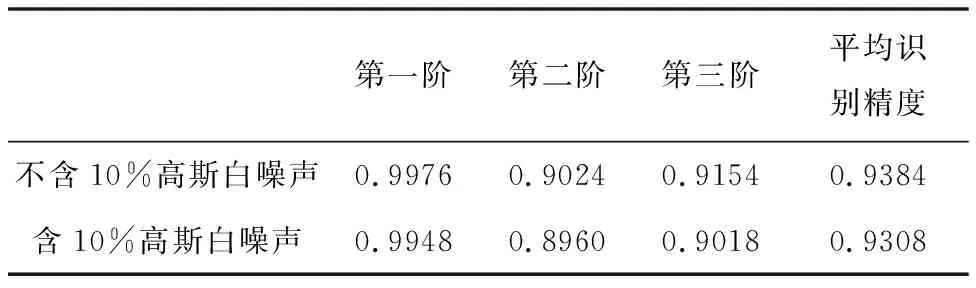
表8 MWNPE识别质量慢时变3-DOF结构的模态振型MACi-avg
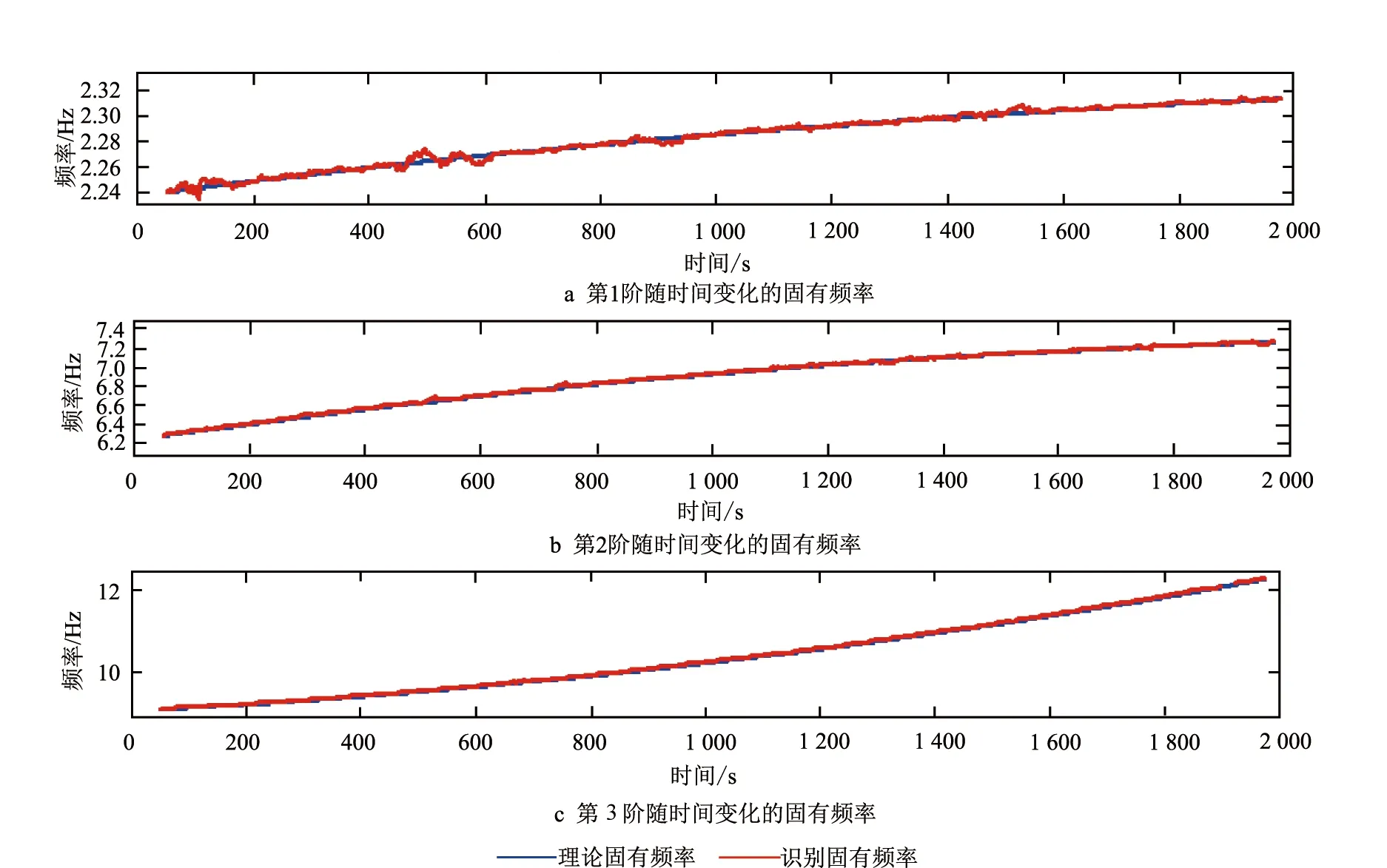
图11 MWNPE算法识别带10%高斯白噪声慢时变3-DOF结构的三阶固有频率变化图
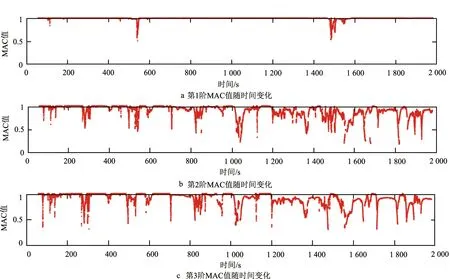
图12 MWNPE识别带10%高斯白噪声慢时变3-DOF结构的三阶模态振型的MACi-avg值变化图
2.4 工作模态参数识别结果分析
(1)由表3~表4,图8~图10可知,MWNPE算法能高精度地识别出线性质量慢时变三自由弹簧振子结构的工作模态参数,并且很好地追踪结构的工作模态参数随时间变化的过程。
(2)由表3可知,MWNPE方法在各阶的未识别窗口总数都低于MWPCA方法,且大幅低于MWEASI方法,说明MWNPE算法存在更少的模态缺失问题,故基于MWNPE方法识别线性慢时变结构的工作模态参数过程中更加稳定。
(3)由表4可知,MWNPE方法相比MWPCA方法,第二、三阶的模态振型识别精度分别提升了0.17%、1.12%,整体提升0.40%。MWNPE方法相比不基于流形学习的MWEASI方法,第一、二、三阶的模态振型识别精度分别提升了41.66%、45.20%、44.61%,整体提升43.72%,这说明MWNPE方法优于MWPCA与MWEASI方法。
(4)由表5~表8、图11~图12可知,MWNPE算法能有效识别带有噪声的线性慢时变结构的工作模态参数,说明MWNPE方法的鲁棒性较强。
3 结束语
本文提出一种仅用振动响应信号识别线性慢时变结构的工作模态参数的方法。实验结果表明,NPE算法能够对时不变结构进行模态分析,识别精度高。滑动窗技术可以将时变结构离散为有限个时不变结构,然后利用NPE算法识别有限个时不变结构的工作模态参数。因此,本文提出利用MWNPE算法识别线性慢时变结构的工作模态参数的创新点在于将滑动窗技术和邻域保留投影算法识别线性慢时变结构的工作模态参数,并与MWPCA、MWEASI方法进行了比较。仿真验证结果表明,MWNPE能有效识别线性慢时变结构的模态参数,且相比MWPCA与MWEASI方法,识别线性慢时变结构工作模态参数精度更高,模态缺失个数更少。
在未来工作中,可通过测量实际结构的位移振动响应数据进一步验证该算法的有效性。除此之外,如何利用非平稳振动响应信号自适应地确定和改变移动窗的固定长度尚未得到完全解决。
