改进NSGA-Ⅱ算法求解考虑运输约束的柔性作业车间节能调度问题
2023-10-12王亚昆刘应波吴永明李少波宗文泽
王亚昆,刘应波,吴永明+,李少波,宗文泽
(1.贵州大学 公共大数据国家重点实验室,贵州 贵阳 550025;2.贵州大学 现代制造技术教育部重点实验室,贵州 贵阳 550025;3.云南财经大学 云南省经济社会大数据研究院,云南 昆明 650231)
0 引言
随着科学技术的发展以及先进制造技术的普及,制造业面临着生存压力,例如人工成本、设备更换、和先进制造观念的更新。为降低生产成本,许多制造企业致力于提高能源利用率和加工效率。为实现这一目标,最高效且低成本的方法就是优化调度。面对市场需求的多样化和加工技术的更新,生产和制造模式也开始朝着方便和灵活的方向发展。在实际生产环境中,生产计划系统往往受多种随机动态事件影响,如车间里各个工件在加工机器之间的运输需要时间、机器故障、意外处理时间、紧急订单的随机到达、订单取消等[1-2]。这些动态事件将导致理想调度与实际加工存在偏差或者不可行。因此,企业要想更加适应于真实环境下的车间调度,考虑动态事件对公司收入和应对不断变化的市场环境具有重要的意义。
多目标柔性作业车间调度是单目标车间调度的扩展,单目标通常以最小化最大制造时间为优化目标[3]。目前,随着客户需求多样化、全球化和环境压力,车间加工过程中必须满足对多个目标约束,例如必须按工期加工完成零件、减少能源消耗或环境影响、考虑加工过程中机器的负载。因此,近几年大量的学者致力于车间调度的多目标研究。GAO等[4]考虑最小化制造时间、最大机器工作量、总工作量3个目标,提出了基于本地搜索改进的遗传算法,并取得了较好的求解效果。李益兵等[5]为减少碳排放量、噪声、和废弃物建立优化完工时间和环境污染程度的模型(Multi-objective Green Flexible Job-shop Scheduling Problem,MGFJSP),并提出改进的人工蜂群算法来求解该模型。DING等[6]提出一种改进的粒子群算法来解决流水车间调度问题(Flexible Job-shop Scheduling Problem,FJSP),并通过改进编码/解码方案、粒子间的通讯机制以及候选机器规则,得到了较优调度方案。YIN等[7]针对灵活的作业车间环境,提出一种新的低碳数学调度模型,该模型可优化生产率、能源效率和降噪。杜士卿等[8]为减少生产时间、保证工件的加工质量、降低车间的能耗建立混合车间调度模型,提出一种最佳觅食算法来求解该模型。LI等[9]提出了能源意识型柔性作业车间调度问题,建立了该问题的数学模型,并使用改进的迁徙鸟算法求解该问题。王建华等[10]针对车间绿色调度问题,建立了优化最大完工时间、机器总负荷、车间能耗3个目标的数学模型,并设计了一种自适应多目标Jaya算法求解该优化问题。
车间加工的环境是复杂的,越来越多的学者关注于车间动态环境,例如:CHEN等[11]研究了带有机器故障的多目标车间调度,建立了以最小化制造时间和总机器工作量的多目标动态调度模型,根据故障机器的处理情况提出一种重调度策略,并采用非支配遗传算法求解该模型。SAHAR等[12]研究了具有随机机器故障的两阶段柔性作业车间调度,同时考虑制造时间和鲁棒性两个目标,并提出帝国主义竞争算法、遗传算法与模拟技术混合解决该问题。GONG等[13]提出一种具有工人灵活性的节能车间调度模型,同时考虑了机器和工人的灵活性以及处理时间、能耗、和工人成本的相关因素,然后提出一种混合进化算法(Hybrid Evolutionary Algorithm,HEA)来解决该模型。LEI等[14]研究了具有间隔处理时间和异构资源的双资源约束的车间调度问题,以最小化碳排放量和最大完工时间为优化目标,提出一种动态邻域搜索算法解决该问题。吴秀丽等[15]提出考虑装卸车间调度问题,以最小化完工时间与装卸时间建立该问题的数学模型,并使用非支配遗传算法求解该问题。GAO等[16]研究了具有模糊处理时间和新作业的插入两个约束条件车间调度模型,并提出一种改进的两阶段人工蜂群算法求解该模型。
在现实的加工环境中,零件的相邻工序不在同一个机器加工,需要车间的运输系统将工件在机器间运输,并且需要一定时间,然而传统的车间调度问题往往忽略工件在机器间的运输约束,近年来,越来越多的学者关注该问题。DAI等[17]提出了一种考虑运输时间的节能作业车间调度问题,最大程度地降低综合能耗和制造期,并设计了一种增强的分布估计算法来解决该问题。HUANG等[18]研究了考虑运输时间的多目标车间调度问题,并混合遗传算法与模拟退火算法求解该问题。ZHANG等[19]以运输时间和处理时间作为独立时间,建立具有运输时间的车间调度模型,并使用改进的遗传算法解决该问题。李香怡等[20]考虑工件在车间加工过程中,运输时间对调度结果的影响,建立最小化完工时间、碳排放量、机器负载的调度模型,并用改进粒子群算法求解该模型。HOMAYOUNI等[21]考虑到车间加工过程中,工件的运输问题常被忽略,提出混合整数线性规划模型来解决该问题,并展示它在求解小型实例最优解的效率。
对考虑运输约束节能柔性作业车间调度问题(Transportation constraint Energy-saving FJSP,TEFJSP)研究处于起步阶段,目前存在如下问题:①关于车间调度研究大多数是多目标优化问题,目标通常为最小化最大完工时间、车间能耗、机器总工作量、碳排放量,但是这些研究中通常忽略工件在不同机器之间的运输这一实际约束,导致求解的调度方案与实际的加工环境有很大的偏差。②目前文献对具有运输约束的车间调度研究缺少相关的通用数学模型、缺少考虑运输约束之后对车间能耗的影响。本文在以上文献研究成果的基础上,提出考虑运输约束车间调度问题,并建立该问题的数学模型,该模型优化最大完工时间、延期、设备总负载、车间总能耗4个目标。③在求解考虑运输约束的柔性作业车间调度问题,传统的编码、解码方法不适用。因此,本文针对该问题建立了考虑运输约束的节能柔性作业车间调度模型,同时设计了新的编码、解码方法。
1 问题描述和数学模型
1.1 TEFJSP问题描述
考虑运输约束的节能柔性作业车间调度问题可以描述为:存在n个待加工工件J={J1,J2,...,Jn},需要在m台机器上进行加工M={M1,M2,...,Mn},每个工件Ji有Ni个工序Oi={Oi,1,Oi,2,...,Oi,Ni}需按顺序加工,每个工序Oi,j可以由该工序的备选加工机器Mi,j⊆M唯一确定的加工。每个工序备选集中的机器加工该工序消耗的加工时间、加工能耗、运输时间均不同。工件Ji的Oj,Ni-1工序在机器Mp上加工完成后,若工序Oj,Ni不在同一台机器上加工,则需要车间的运输系统AGV将该工件运输到下一工序加工的机器Mq加工,并且AGV需要消耗能量。AGV在不同的机器之间运输工件花费的时间不同,消耗的能耗也不同。TEFJSP为每个工序选择唯一的机器加工和确定每个机器加工各个工序的开始时间和结束时间,并确定每个工件相邻加工工序在各个机器间的运输时间,TEFJSP约束条件如表1所示。

表1 TEFJSP约束条件
1.2 TEFJSP符号定义
TEFJSP符号及意义如表2所示。

表2 TEFJSP符号定义
1.3 TEFJSP数学模型
该模型中变量定义以下:
Cj,h为工序Oj,h完工时间的连续变量。
车间调度的数学模型表示如下:

(1)
式中:ML为机器负载,TE为车间总耗。
车间在加工这批零件时需要消耗的总能量主要包括机器加工能耗(Ebusy)、机器空转能耗(Eidle)、运输能耗(Etran)和其他能耗(Eother)4个部分。
(2)

(3)
Etran=∑T×Wtran;
(4)
Eother=Cmax×Wother。
(5)
其他约束:

(6)
(7)
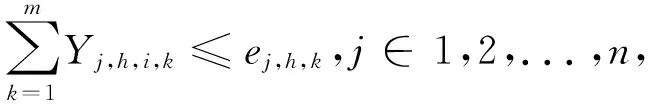
(8)
Yj,1,0,k≤ej,1,k,j∈1,2,...,n,k∈1,2,...,m;
(9)

(10)
Yj,2,i,k≤Yj,1,0,i,j∈1,2,...,n,k,i∈1,2,...,m;
(11)

(12)

(13)
Cmax≥Cj,nj,j∈1,2,...,n;
(14)
Ti,j,h≥0,i∈1,2,...,m,j∈1,2,...,n,h∈1,2,...,nj;
(15)
Cj,h≥0,Cl,z≥0,j,l∈1,2,...,n,h,z∈1,2,...,nj;
(16)
Xi,j,h,Yj,h,i,k,Xl,z,j,h∈{0,1},i,k∈1,2,...,m,j,l∈1,2,...,n,h∈1,2,...,nj。
(17)
其中:式(6)约束每一个工序仅分配给一台机器加工;式(7)约束任意工件的第一个工序Oj,1由虚拟机器0运输到工序Oj,1的加工机器Mi加工;式(8)和式(9)约束工序Oj,h的加工机器必须在该工序备选机器中选择;式(10)和式(11)约束工序Oj,h在机器Mi上加工,工序Oj,h+1在机器Mk上无干扰加工;式(12)和式(13)约束工序Oj,h完工时间不小于Oj,h-1的完工时间与Oj,h的运输时间、加工时间之和;式(14)约束最大完工时间不小于每个零件的完工时间;式(15)约束工序在每个机器之间的运输时间不小于0;式(16)约束每个工序的完工时间不小于0;式(17)约束相关变量为二进制变量。
2 改进NSGA-Ⅱ求解TEFJSP
2.1 编码
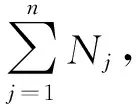

图1 染色体编码
如图1所示,染色体长度L=8,工序编码层顺序为“2 1 3 3 3 1 2 1”,其中第1个位置数字“2”表示工序O2,1,第2个位置数字“1”表示工序O1,1,第4个位置数字“3”表示工序O3,2。基于机器编码为“2 1 3 4 4 2 1 3”,第1个位置“2”表示工序O2,1在机器M2上加工,第2个位置数字“1”表示工序O1,1在机器M1加工,第4个位置上“4”表示工序O3,2在机器M4加工。运输时间层编码为“0.8 0.5 0.6 1 0 0.9 1.3 1.4”,第一个位置数字“0.8”表示加工工序O2,1从虚拟机器M0运输0.8到机器M2加工,第2个位置数字“0.5”表示加工工序O1,1从虚拟机器M0运输0.5到机器M1加工,第4个位置数字“1”表示加工完成工序O3,1需要运输1运输到工序O3,2的加工机器M4。该染色体所对应工序的加工顺序为:O2,1(M2,0.8)-O1,1(M1,0.5)-O3,1(M3,0.6)-O3,2(M4,1)-O3,3(M4,0)-O1,2(M2,0.9)-O2,2(M1,1.3)-O3,1(M1,1.4),括号中为该工序使用机器和运输时间。
2.2 解码
解码是将编码转化成调度方案,传统插入式贪婪解码方法不再适用于求解TEFJSP[22],本文设计一种考虑运输约束插入式贪婪解码方法。具体解码方法如下:
(1)工序Oj,1是工件J的第一个工序,且工序Oj,1对应的加工机器Mi是首次使用,则工序Oj,1从虚拟机器“0”运输到工序Oj,1加工机器Mi后直接开始加工。
(2)工序Oj,h非工件J第一个工序,且工序Oj,h对应的加工机器Mi是第一次使用,则工序Oj,h -1加工完成后运输到机器Mi即刻开始加工。
(3)工序Oj,h非工件J第一个工序,且工序Oj,h加工使用机器Mi也非第一次使用,在使用可插入式解码时必须考虑工序在机器加工时产生的空闲时间,例如机器Mi加工k个工序,则会产生k个空闲时间,考虑这些空闲时间是否满足工序Oj,h插入加工分为以下几种情况:
1)满足可插入式解码第1种情况如图2所示。
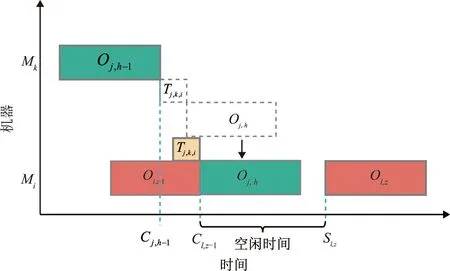
图2 工序Oj,h可插入式解码第1种情况
Cj,h-1+Tj,k,i≤Cl,z-1;Cl,z-1+Pj,h,i≤Sl,z。
(18)
该种情况工序Oj,h在机器Mi加工,Mi空闲时间与工序Oj,h加工时间和运输时间满足约束式(18),此时工序Oj,h在机器Mi的开始加工时间Sj,h=Cl,z-1。
2)满足可插入式解码的第2种情况如图3所示。
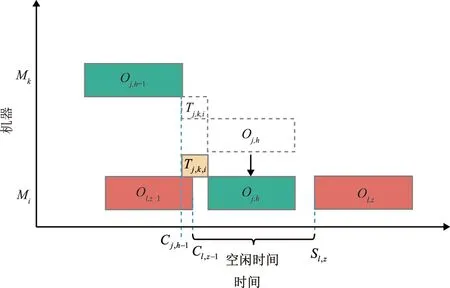
图3 工序Oj,h可插入式解码第2种情况
Cj,h-1≤Cl,z-1;Cj,h-1+Tj,k,i≥Cl,z-1;Cj,h-1+Tj,k,i≤Sl,z。
(19)
该种情况工序Oj,h在机器Mi加工,Mi空闲时间与工序Oj,h加工时间和运输时间满足约束式(19),此时工序Oj,h在机器Mi开始加工时间Sj,h=Cj,h-1+Tj,k,i。
3)满足插入式解码的第3种情况如图4所示。

图4 工序Oj,h可插入式解码第3种情况
Cj,h-1≥Cl,z-1;Cj,h-1+Tj,k,i+Pj,h,i≤Sl,z。
(20)
该种情况工序Oj,h在机器Mi加工,Mi空闲时间与工序Oj,h加工时间和运输时间满足约束式(20),此时工序Oj,h在机器Mi开始加工时间Sj,h=Cj,h-1+Tj,k,i。
4)不满足插入式解码的情况如图5所示。

图5 工序Oj,h不满足可插入式解码
Cj,h-1+Tj,k,i+Pj,h,i>Sl,z。
(21)
这种情况机器Mi的空闲时间不足以满足工序Oj,h插入加工,因此工序Oj,h安排在机器还未使用时间段,工序Oj,h开始加工时间Sj,h=Cl,z。
2.3 帕累托分级排序
非支配排序遗传算法(Non-dominated Sorting Genetic Algorithms,NSGA)是由SRINIVASAN等[23]在1994年提出,该算法采用分级选择算法选择出优秀个体,在迭代过程中采用小生境法维持优秀个体的稳定性。NSGA-II算法的非支配排序是根据种群内各个个体的支配关系划分为不同的支配前端,支配关系反映了个体的优劣程度,通过支配关系和拥挤度筛选出种群中优秀个体。非支配排序后得到X个非劣前沿(用P1,P2,...,PX表示),各个非劣前沿满足以下性质:
(1)∀h,f∈{1,2,...,X},且h≠f,Ph∩Pf=∅,非支配排序后种群中各个个体相互独立。
(2)U∈{P1,P2,...,PX}P=Pop,非支配排序前后种群规模不变。
(3)P1>P2>…>PX,非支配排序后种群分成X个非劣前沿。
种群中每个个体进行非支配排序后对应两个参数,个体h所支配个数,用sh表示;支配个体h个数,用nh表示。则有:
nh=|{z|z≻h,h,z∈Pop}|;
sh=|{f|h≻f,h,f∈Pop}|。
种群中nh=0的个体记为非支配前沿F1,记F1中的个体rank值为1;将F1中的其他个体按nz=nz-1=0的规则分配至下一等级非劣前沿,每次迭代均遍历种群中所有个体,为每个个体分配对应非劣前沿。
2.4 选择
经过帕累托分级排序后,种群中每个个体都分配一个非劣前沿等级号。个体适应度值越优,非劣前沿等级号越小,可以通过比较非劣前沿等级号来选择较优个体。本文采用锦标赛法,设置两名选手进行参赛,比较两个参赛选手的非劣前沿等级号,值较小的个体获胜直接遗传到下一代。如果两个参赛选手非劣前沿等级号相同,采用小生境技术选择较小拥挤度个体保留到下一代。迭代l代第t个目标函数最佳小生境计算方法[24]如下:
(22)
式中:flt为迭代l代第t个目标的函数值,n为目标个数,Pop为种群规模。
2.5 交叉与变异
本文染色体的编码方式采用三层矩阵编码,一条染色体包含工序加工顺序信息、机床选择信息、运输时间信息。染色体在进行交叉、变异操作时,工序的加工顺序发生变化或工序加工选择的机器发生变化时,运输时间编码层的基因可能会发生变化,而工序层编码和机器层编码确定后运输时间编码层的基因就已经确定,因此工序编码和机器编码为显性基因参与交叉、变异操作,运输时间编码为隐形基因不参与交叉、变异操作,但是该基因随显性基因的变化自我调整。因此本文的交叉和变异操作主要有工序编码层的交叉和变异操作和机器编码层交叉和变异操作。
(1)工序编码层交叉操作 染色体执行工序的交叉操作,只改变工序的加工顺序,不改变每个工序加工使用机器。例如有N个工件,随机生成集合n,满足n⊆{1,2,...,N},n中元素为染色体的稳定基因,父代P1、P2找出集合n中表示的工件在染色体上的位置和顺序,直接遗传给后代,未被选中的父代基因交换后按顺序的插入到子代中,运输时间编码层重新调整后生成新的子代。3个工件8个工序两条有效染色体,随机生成的集合n={1},工序编码层交叉过程如图6所示。
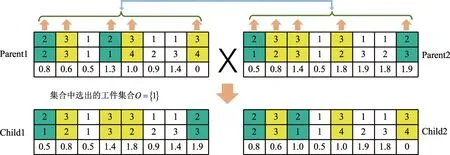
图6 工序编码层交叉操作示意图
(2)机器编码层交叉操作 染色体执行机器的交叉操作,只改变工序使用的加工机器,不改变工序的加工顺序。例如有N个工件,随机生成一个集合n,满足n⊆{1,2,...,N},父代P1、P2找出集合n中表示的工序对应的加工机器,将对应工序加工机器互换,调整运输时间生成新的个体。这种机器编码层交叉操作简单、易于实现,并且能够保证染色体的有效性。3个工件8个工序的两条有效染色体,随机生成的集合n={1},机器编码层交叉操作过程如图7所示。

图7 机器编码层交叉操作
NSGA-Ⅱ算法在求解多目标优化问题时很容易陷入局部最优,为解决该问题,算法在跌代过程中,迭代前期希望变异率较小有利于保留较优的个体,迭代后期希望变异率较大有利于避免“早熟”。因此本文采用自适应变异率。迭代l代的变异率如式(23)所示:
(23)
式中:l为迭代次数,lmax为最大迭代次数,k1设置变异率最小值,k2设置变异率最大值。
(3)工序编码层变异 染色体的工序编码发生变异时,对应工序使用的加工机器不变。为保证染色体的有效性,本文采用两点互换式变异。操作过程如下:
步骤1随机生成在染色体范围内的两个位置点。
步骤2将两个位置工件对应的加工机器编码存储在两个变量variable1,variable2中。
步骤3将两个位置的工序互换。
步骤4两个工件加工机器编码按照var1、var2机器的顺序对应插入。
步骤5调整染色体的运输时间,生成新的染色体。
工序编码层操作过程如图8所示。
(4)机器编码层变异 随机选择染色体上的一个位置,将该位置机器编码层基因突变,突变方式为从该工序的备选机器中选择一个机器替换原机器。如图9所示,3个工件8个工序的两条有效染色体,随机生成的突变位置为4,该染色体位置对应的工序为O2,2,可以加工该工序的机器为M1M2M3M4,目前加工该工序的机器为M1,从该工序的备选机器中选择新的加工机器为M3。
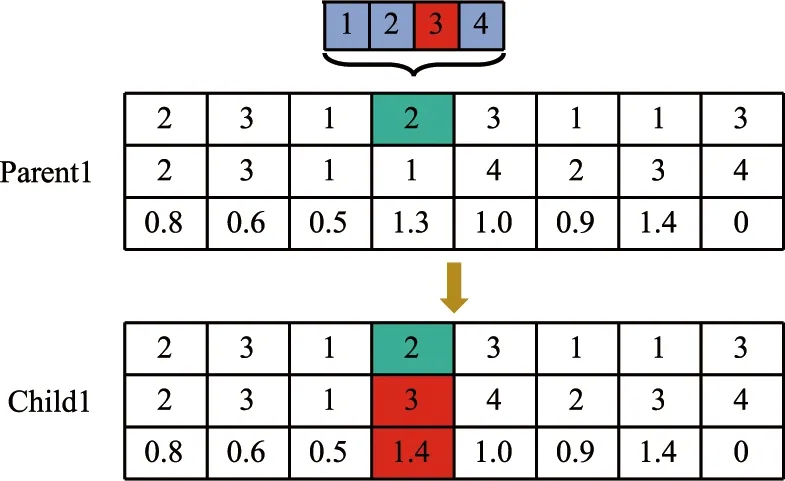
图9 机器编码层变异操作

图10 学习生成后代示意图
2.6 学习
NSGA-Ⅱ随机生成染色体、交叉、变异都有一定的盲目性,大多情况下陷入局部最优解不能跳出,为解决该问题本文引入的学习机制改进NSGA-Ⅱ。学习机制是子代学习前代最优解染色体优良基因,提升子代个体的良率。最优解在工序编码、机器编码均属于较优基因,后代对最优解的学习,继承了最优解的这些信息,加快算法求得全局最优解的速度。学习机制执行过程如下:
步骤1从最优解染色体长度范围内随机选择两个位置。
步骤2将两个位置之间的基因段直接复制给子代对应染色体位置。
步骤3剩余左侧的基因段打乱顺序后赋值给子代左侧基因段,剩余右侧基因段打乱顺序后赋值给子代右侧基因段,根据工件在机器之间的运输时间,调整运输时间编码层生成新的子代染色体。
引入学习机制的NSGA-Ⅱ算法记为(Learning-NSGA-Ⅱ,L-NSGA-Ⅱ),每代学习操作生成个体数记为Lc。采用子代学习父代优良信息改进的NSGA-Ⅱ,加快算法获得全局最优解的速度,改善NSGA-Ⅱ算法的性能。
2.7 选择最优加工方案
由于最大完工时间、能耗、总延期、设备总负载各目标之间存在对立,在多目标优化问题中不存在单一的最优解决方案[25],众多最优方案之间相互非支配,组成帕累托前沿。从帕累托前沿中决策出最优方案的方法有很多,其中最流行的就是归一化加权法,该方法具有简单性和高效探索能力,常用于生产调度多目标决策问题。具有t个目标归一化加权法定义为:
(24)
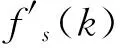
(25)
式中fs,max与fs,min分别为目标fs的最大值和最小值。
求解多目标决策问题时,决策者往往针对各个目标的重视程度不同,而赋予各个目标不同权重,以示对该目标的重视程度。但是多目标问题中往往对一些目标有一些特殊的要求,例如在多目标车间调度问题中,多目标包含总延期时,如果订单不能如期完成,不但会对工厂有很严重的惩罚,而且会影响工厂的信誉,因此车间调度的多目标问题涉及到总延期的目标,通常该目标约束为0。为了适应对多目标问题选择出最优加工方案对某一目标有特殊要求,本文采用从帕累托前沿剔除法,先从帕累托前沿剔除不符合要求的方案,再采用归一化加权法选出最优的加工方案。L-NSGA-Ⅱ算法执行过程如图11所示。
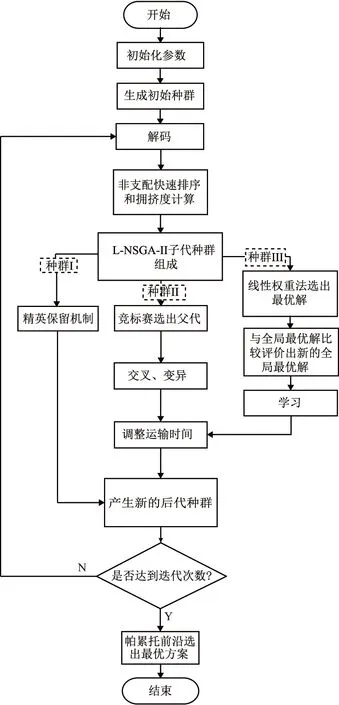
图11 L-NSGA-Ⅱ算法的执行过程
3 仿真实验分析
为了测试L-NSGA-Ⅱ算法的性能,在处理器为Intel(R) Core(TM) i5-6500 CPU @ 3.20 GHz,基带RAM 8.00 GB,64位Win 10操作系统,安装MATLAB R2018a的实验环境,测试Kacem算例[26]、Brandimarte算例[27],这两组算例包含的工件数从3~15不等,机器从5~10不等,测试该算法在求解小型算例、中型算例、大型算例的性能。这两组算例中仅包含工件在各个机器的加工信息,本文随机生成运输时间,15台机器间的运输时间如表3所示,机器的能耗信息如表4所示,经多次实验最优组合参数设置为:种群数量Pop=100、迭代次数lmax=200,最小变异率k1=0.1,最大变异率k2=0.8,交叉率px=0.8,学习生成子代个数Lc=20。目标权重参数为:总延期为0,最大完工时间权重w1=0.5,设备总负载权重w3=0.2,车间总能耗权重w4=0.3。
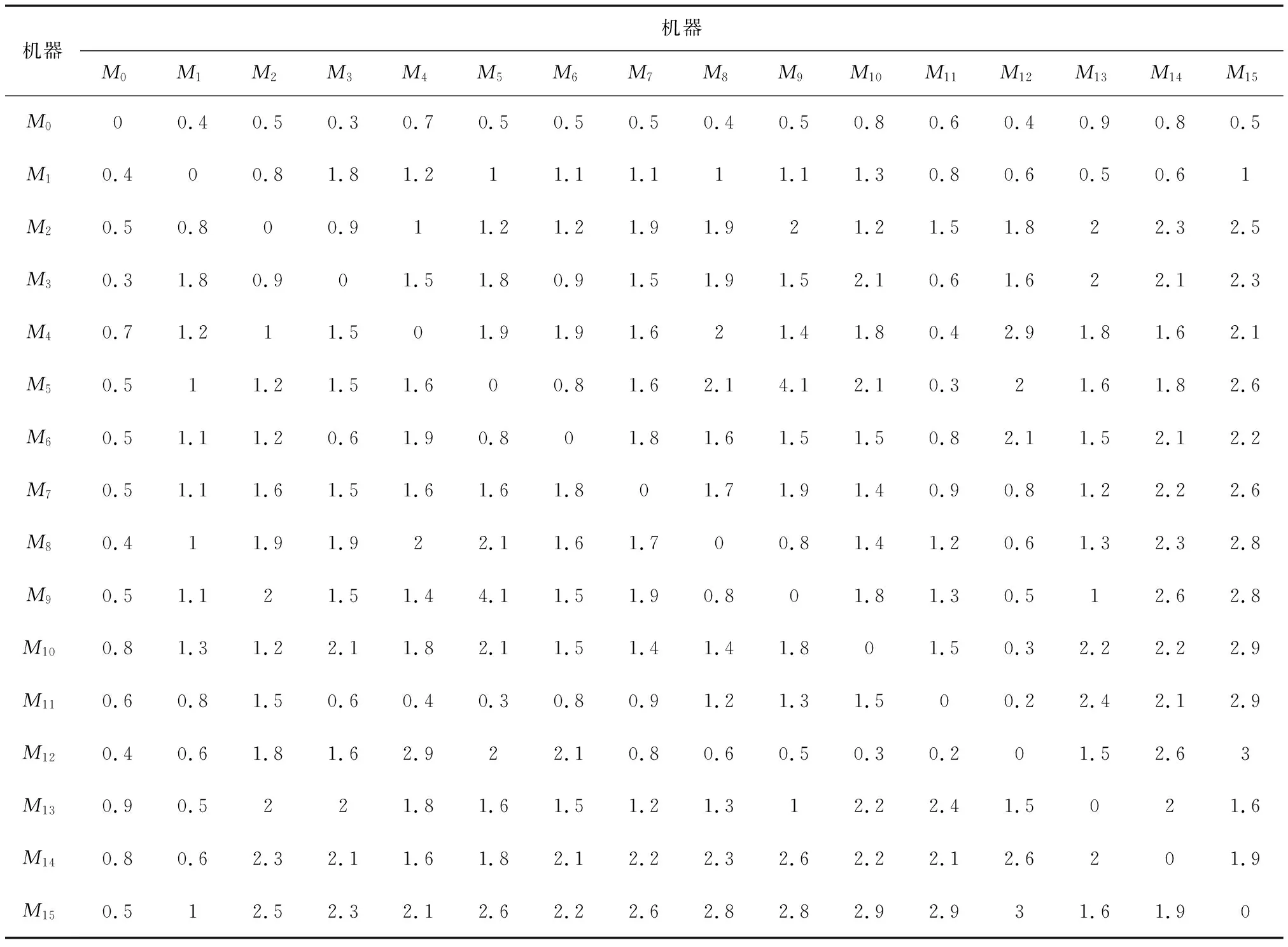
表3 机器之间的运输时间 s

表4 加工机器的能耗信息 kW/h
Kacem与Brandimarte算例求解结果如表5所示,TEFJSP相较于FJSP在完工时间、总能耗均有明显增多,并随着算例规模的增大,完工时间和总能耗偏差更大。采用L-NAGA-Ⅱ算法求解TEFJSP相比于NAGA-Ⅱ算法有明显优势,两组算例中有13个算例在最大完工时间求解的目标值较优、9个算例在设备总负载求解的目标值较优,13个算例在车间总能耗求解的目标值较优,11个算例在求得最优解体现出更高的效率。体现出L-NAGA-Ⅱ算法在求解TEFJSP时的优越性能。

表5 Kacem与Brandimarte算例求解结果
Brandimarte组第4个算例KM04不考虑运输约束调度甘特图如图12所示,该算例考虑运输约束车间调度甘特图如图13所示,NSGA-Ⅱ与L-NSGA-Ⅱ求解该算例TEFJSP问题迭代过程图如图14所示。KM04算例FJSP调度方案求解结果为:最大完工时间72,总延期0,设备总负载343,能耗总量99.31 kW,TEFJSP问题的求解结果为:最大完工时间72.6,总延期0,设备总负载344,能耗总量119.34 kW。从两问题的求解结果可以看出,TEFJSP问题的调度方案最大完工时间延后0.6,能耗总量增加20.03 kW。NSGA-Ⅱ与L-NSGA-Ⅱ算法求解TEFJSP问题迭代过程图如图14所示,实线的迭代过程为L-NSGA-Ⅱ算法的迭代过程,该算法迭代49代时求得最优权重适应度140.901,虚线迭代过程为NSGA-Ⅱ算法的迭代过程,在迭代至48代时陷入局部最优解。

图12 MK04算例不考虑运输约束调度甘特图

图13 MK04算例考虑运输约束调度甘特图

图14 KM04算例NSGA-Ⅱ与L-NSGA-Ⅱ迭代过程图
4 结束语
本文针对传统柔性作业车间调度通常忽略加工过程中工件在各个机器之间的运输时间等约束问题,提出了考虑运输约束的节能柔性作业车间调度问题并建立该问题的数学模型,该模型优化车间加工过程中最大完工时间、总延期、设备总负载、车间总能耗4个目标,并提出了更优性能的L-NSGA-Ⅱ算法求解算法,即染色体四层矩阵编码与可插入式解码方法能更好地反映具有运输约束的车间调度问题,同时获得了更优的车间调度方案。最后,未来研究希望探索一种更优性能的多目标算法解决考虑运输约束的柔性作业车间节能调度问题。
