绿色供应链技术创新与合作伙伴选择决策研究
2023-10-12袁柳洋
段 炼,袁柳洋,2+
(1.武汉科技大学 理学院,湖北 武汉 430065;2.武汉科技大学 湖北省冶金工业过程系统科学重点实验室,湖北 武汉 430081)
0 引言
随着经济全球化的发展,自然资源愈显匮乏,环境污染和能源消耗问题愈发严重,因此推动环境保护,促进可持续发展成为世界各国不得不重视的问题。同时,随着消费者市场需求的改变,即消费者逐渐青睐于绿色环保产品,经济模式也在随之改变,在此基础上,考虑资源短缺和绿色低碳问题的绿色供应链应运而生[1]。为了实现全面可持续发展,并在激烈的竞争局势中赢得优势地位,企业对传统供应链进行绿色改造以转型,从而树立绿色环保理念是势在必行的。
在供应链绿色转型过程中,绿色技术的创新是当今研究的热点话题。绿色技术创新是绿色供应链管理中的重要内容之一,也是可持续发展研究重要问题。绿色技术创新一般是管理创新和技术创新的统称,其目标是协调人类与环境的关系。同时,企业的绿色技术创新也可以保证社会福利的稳定[2]。
在绿色供应链中,合作伙伴的选择是绿色供应链管理重要的一环,也是绿色供应链成功运行的关键,但现有研究在分析绿色供应链合作伙伴选择时往往会忽略供应链成员间的利润分配问题,通常是将两者分割开来单独研究。而在现实情况中,绿色供应链的创新行为是多目标收益主体和多目标策略问题,考虑且满足成员间的资源配置和收益分配的情况可以避免收益纠纷与冲突。进一步地,绿色供应链合作伙伴选择除了考虑收益分配需求,还要斟酌绿色技术创新等一系列决策。因此,本文聚焦的主要问题如下:①绿色供应链中供应商如何选择合作的制造商?②供应商是否会选择共享绿色技术,以及制造商是否会选择绿色技术创新?③组成的绿色供应链如何进行收益分配?
为了回答上述问题,本文构建了两型博弈模型来研究由一个供应商和三个制造商组成的两级绿色供应链问题,分两种情况来考虑:制造商不进行绿色技术创新和制造商进行绿色技术创新。然后基于逆向归纳法,分别得到供应商和制造商的最优策略。
本文的创新和贡献主要包括以下两个方面:
(1)从供应商的角度出发,研究供应商是否选择共享绿色技术,以及如何选择合作的制造商;从制造商的角度出发,研究制造商是否进行绿色技术创新,以及创新投入量。以往的研究大多用合作博弈或者非合作博弈对这类问题进行研究,而本文采用两型博弈的模型对其合作和绿色技术创新问题进行了分析,并考虑到绿色供应链成员的预期收益分配。
(2)在两型博弈的合作博弈阶段,针对绿色供应链收益分配时收益函数特征值缺失的情况,本文采用宗系解分配收益更为合理,也可以使分配更为公平,更符合实际情况。
1 文献综述
经济全球化竞争导致绿色产品更新迭代快、需求波动大[3],且随着环境的变化,绿色供应链研究的视角也在发生变化。与本文研究相关的文献主要有以下几个方面:
(1)对于绿色供应链的技术创新问题 HABIBA等[4]研究了金融发展、绿色技术创新和可再生能源使用对碳排放量的影响,结果表明绿色技术创新和可再生能源的使用将是导致碳排放量下降的主要因素。WANG等[5]通过构建绿色技术创新升级的经济绩效传导模型,发现绿色工艺创新和绿色产品创新能够有效提高企业的经济效益,研究结果加深了对绿色技术创新过程的理解,对优化绿色发展政策设计具有启示意义。DENG等[6]在是否有政治竞争的两种情景下,采用博弈论和优化理论分析了企业的最优绿色技术创新战略。温湖炜等[7]采用倍差法,基于环境税费征收标准考察了环境税费政策干预的异质性效应,并探讨环境保护税改革对企业绿色技术创新的影响。ROH等[8]研究了绿色管理创新、绿色营销创新等内部绿色活动对促进企业实现环境绩效影响。LI等[9]对具备不同研发能力的两类企业与银行之间进行了三方演化博弈分析,得出了市场化环境监管政策与企业绿色技术创新实施间的影响关系。
(2)对于合作伙伴选择的问题 胡丽辉等[10]结合企业能力与绿色环境两个方面建立绿色供应链合作伙伴选择的评价体系,借助TOPSIS法从众多备选合作伙伴中选择适合自身的伙伴。常香云等[11]通过建立模糊多目标决策模型来选择其合作伙伴。AMID等[12]择优选择合作伙伴则是通过建立模糊多目标线性模型,应用模糊决策方法对合作伙伴进行择优评价。WU等[13]提出了结合分析网络过程(Analytic Network Process,ANP)和多目标规划(Multi-Objective Programming,MOP)的方法对绿色供应链合作伙伴的选择构建了模型。周向红等[14]构建了多源异构VIKOR群决策方法以解决在云制造模式下协同创新伙伴选择评价指标体系不完善等问题。
(3)对于利润分配问题 该问题是绿色供应链伙伴选择也是合作博弈中重要的问题之一,合理公平的收益分配对供应链成员的创新活动具有重要的意义。多数学者在利润分配时采用改进的Shapley法[15-17],也有学者采用核仁[18]、CIS值[19]等作为利润分配方案。而对于有3个或以上成员参与的合作博弈,学者大都选择Shapley值进行求解,这也是目前最为广泛的求解方式,但是其存在着计算复杂和难以估算缺失特征值的问题。
通过上述文献可以看出,现有研究大都采用非合作博弈理论、演化博弈理论、评价体系等方法对供应链成员绿色技术创新与合作伙伴问题进行分析,且将两个问题分开研究,还忽视了收益分配因素对供应链成员决策的影响。与之不同的是,本文采用BRANDENBURGER等[20]提出的非合作-合作两型博弈理论(简称两型博弈),将绿色技术创新问题与合作伙伴选择问题放在同一个框架中研究,该方法将合作博弈和非合作博弈进行统筹化一,在考虑绿色供应链成员决策的同时兼顾了收益分配对决策产生的影响,可以很好地解决竞争元素和合作元素共存的绿色供应链问题。同时,两型博弈模型在供应链问题以及其他问题中都有着较好的应用[15,21-24],这些应用也为本文研究的可行性提供了支持。而对于利润分配问题,尽管Shapley值的应用十分广泛,但其依然具有一些不可忽视的问题,因此,本文采用胡石清[25]提出的结合“占优”和“平均”方法的合作博弈新解——宗系解的概念,不但解决了特征值缺失和Shapley不满足个体合理性的问题,而且计算方便简洁。
综上所述,绿色供应链成员的决策和收益分配问题受到了广泛的关注。然而,鲜有文献将两型博弈模型运用到企业绿色技术创新与合作伙伴选择的问题中,鉴于此,本文用两型博弈模型研究了由一个供应商和三个制造商组成的两级绿色供应链中合作与绿色技术创新问题。分别研究了只考虑供应商是否选择共享绿色技术策略以及收益分配的两型博弈模型;同时考虑供应商是否选择共享绿色技术的策略和制造商是否选择绿色技术创新的策略以及收益分配的两型博弈模型。用非合作博弈分析了供应商和制造商的决策;用宗系解分配合作成功的供应商和制造商所得的收益。
2 问题描述与基本理论
2.1 问题描述与假设
在绿色供应链中,供应商要向制造商提供生产的原材料,该材料要保证供应活动的绿色性且满足制造商的要求,如中兴通讯需要供应商提供的原材料满足其《禁止和限制使用的环境物质要求》的要求。上游供应商为响应国家的号召和满足制造商的需求,会更早地进行绿色技术创新,因此本文研究的供应商绿色集成度较高且具备一定的技术规模,从而供应商可以选择以一定的成本为制造商提供共享其绿色技术的便利条件,使得制造商可以进一步提高产品的绿色度,进而影响消费者对其产品的支付意愿。下游制造商主要通过绿色产品设计、绿色工艺和废弃物回收处理等创新活动来提升产品的绿色特性,根据供应商提供的绿色原材料进行绿色制造。本文研究由一个供应商s和三个制造商i(i=m,n,o)组成的两级绿色供应链,其中供应商向制造商提供生产的原材料,原材料的数量、质量和绿色度对产品的最终质量和绿色度有着重大的影响。因此,供应商对制造商的长远发展有着至关重要的影响。为防止市场产品过剩和保护双方商业机密,供应商只可以选择两个制造商提供绿色原材料并进行合作。不失一般性,将供应商选择的两个制造商看作一个小联盟,则供应商的决策是在3个小联盟即mn/mo/no中选择可使自身利益最大化的那个合作伙伴。本文考虑的合作与绿色技术创新问题主要分为两种情况:①供应商在向制造商提供绿色原材料的时候考虑是否选择共享绿色技术并考虑合作伙伴的选择,然后进行收益的分配;②供应商在向制造商提供绿色原材料时考虑是否选择绿色技术的共享,并考虑合作伙伴的选择,制造商则需要考虑它们自身是否要进行绿色技术创新,然后再进行收益的分配。
为方便本文分析,提出如下研究假设,本文所用到的符号说明如表1所示。
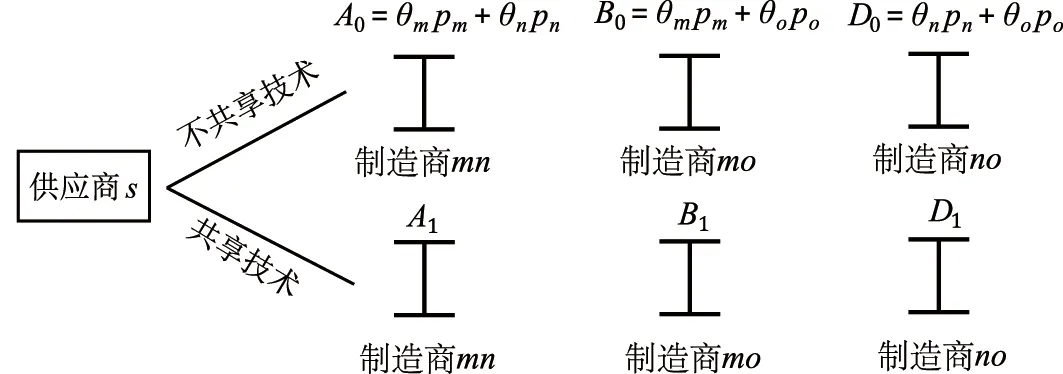
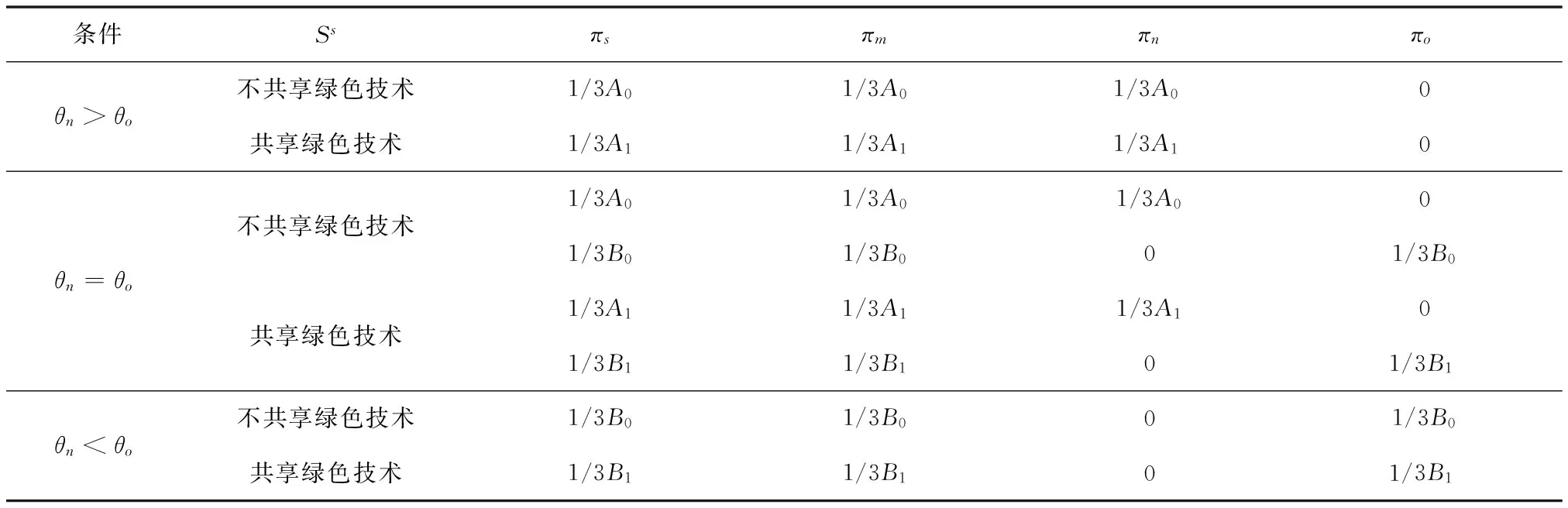
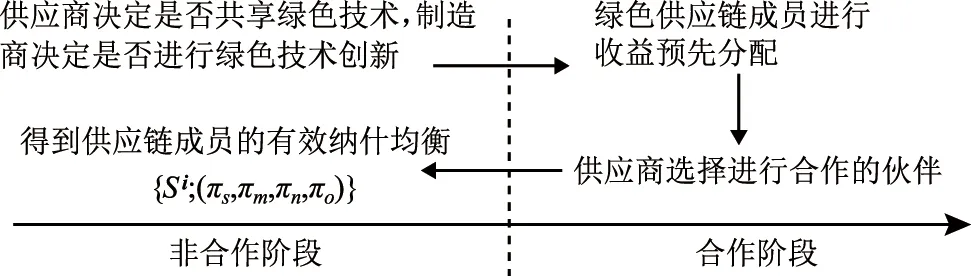
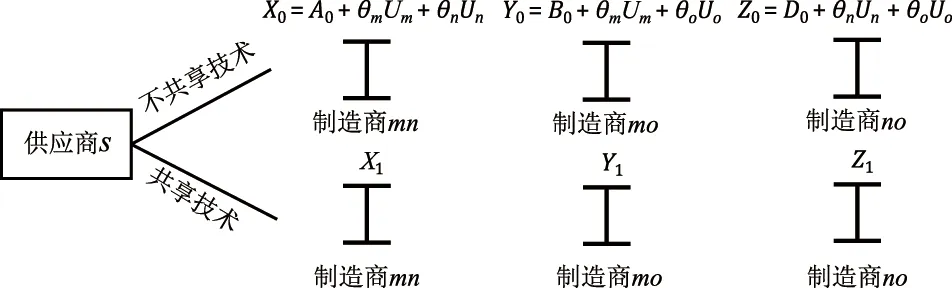
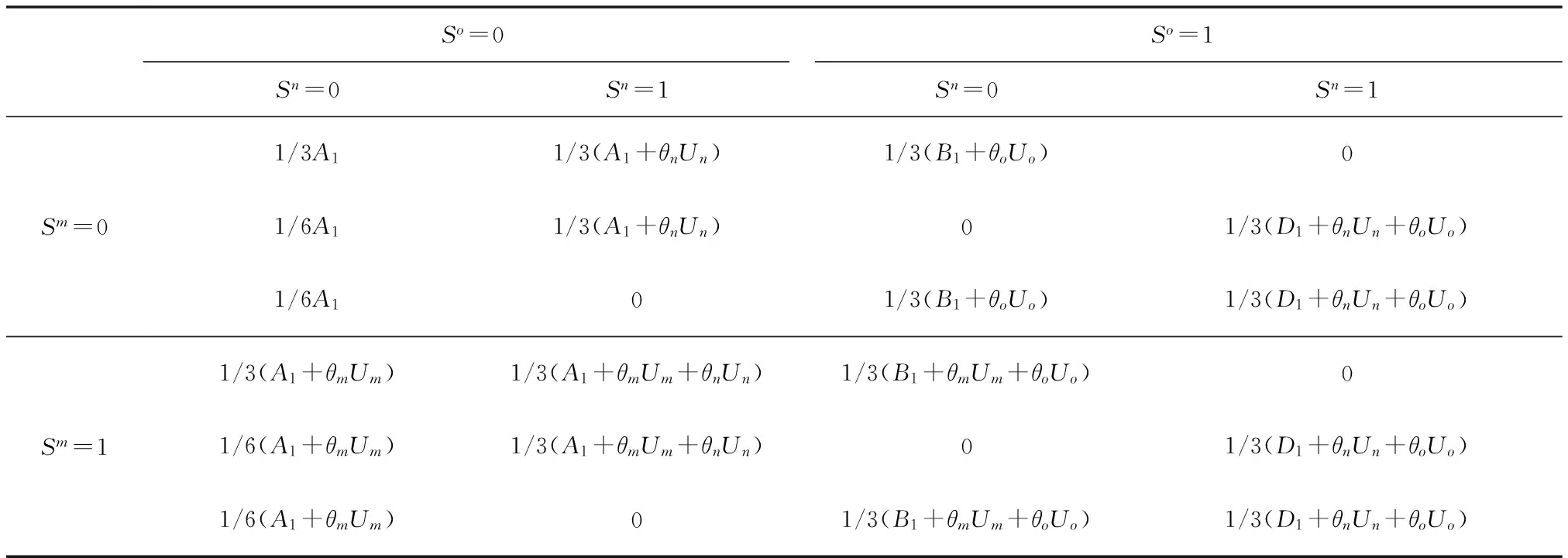
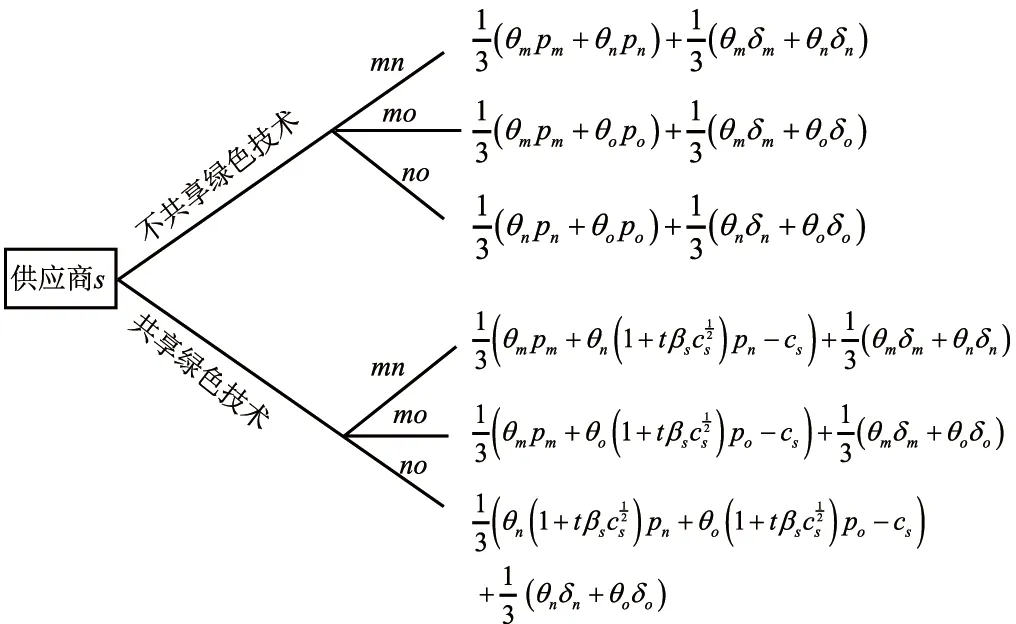
假设1在绿色供应链中,实际各制造商之间的差异性会使其市场地位有所不同,从而消费者的消费偏好会有一定的差异。假设制造商生产的产品绿色度均为g,但制造商m是所有下游制造商中能力最强、消费者认可程度最高的,因此消费者愿意以较高的价格pm购买其产品。制造商n和o则相对于制造商m是能力较弱,知名度和消费者的认可程度较差的,因此消费者对他们产品的支付意愿相对也较低,消费者只愿意以较低的价格pn和po购买其产品,不妨令pn=po 假设4供应链的存在本身具有不确定性,因为一些原因可能会导致供应链中断,如供应商不能按时提供原材料,制造商不能按时开工等,特别是在公共突发事件的影响下,供应链中断的情况比比皆是[30]。本文只考虑制造商可能会产生一定的中断风险,即设制造商i(i=m,n,o)不发生中断的安全系数为θi,不妨设θm>θn,θo,则两个制造商均不中断的概率为θiθj(i,j=m,n,o,i≠j),只有一个制造商不中断的概率为θi(1-θj),两个制造商均发生中断的概率为(1-θi)(1-θj)。 本文采用BRANDENBURGER等[20]提出的两型博弈模型研究绿色供应链中参与企业既存在策略选择(是否共享绿色技术/绿色技术创新)又存在利润分配(预期收益分配)的问题,其定义如下: 定义1两型博弈[20]。设绿色供应链成员集合为N={1,2,…,n}(n≥2),ρ(N)是集合N幂集,对于任意成员的联盟A⊆N,两型博弈记为: (S1,…,Sn;V(s)(A);φ1,…,φn)。 (1) 其中:i为参与成员,对于∀i∈N,si是其选择的策略,成员i的策略集合是Si,有s=(s1,s2,…,sn),S=S1×S2×…×Sn;A为成员的联盟,对于每个联盟A⊆N,成员i选择策略si,特征函数是V(s)∶ρ(N)→R,则V(si)(A)是N的所有子集A上的实值函数,即联盟A的收益,通常情况下V(si)(∅)=0,∅表示空集;对于∀i∈N,0≤φi≤1,其中φi为成员i的信心指数。 本文采用胡石清[25]提出的合作博弈的宗系解进行收益分配,有关宗系解的概念如下。 定义2宗系[25]。在一个n人合作博弈V(s)(N)中,对于某个局中人i,含有i的联盟共有2n-1个,其中联盟平均值最大的联盟,称为局中人i的宗系。 所有局中人的宗系构成的联盟集合,称为该博弈的有效联盟。而有一些联盟,其联盟均值不是任何局中人按平均分配原则所能分配到的最大值,这些联盟被有效联盟占优,称为无效联盟。 定义3纯宗系、混合宗系[25]。在合作博弈的有效联盟中,若一个联盟是其所有成员的宗系,则称该联盟为纯宗系;若一个联盟是其一部分成员的宗系,而对于另一部分成员来说,该联盟不是其宗系,则称该联盟称为混合宗系。 定义4准宗系[25]。对于某个局中人i,在无效联盟中寻找包含i并且联盟平均值最大的联盟,若该联盟是其所有成员在无效联盟中联盟平均值最大的联盟,称这个无效联盟为这些成员的“准宗系”。若不是,局中人i只能退而求其次,直到在剩余联盟中找到包含联盟平均值最大,并且该联盟是其所有成员在在剩余联盟中联盟平均值最大的联盟,该联盟也被称为其成员的“准宗系”。 准宗系是一定存在的,当局中人最后退步到自己单干,单人联盟就是自己的准宗系。 定义5宗系核[25]。在一个n人合作博弈V(s)(N)中,基于博弈的宗系所求的解集为宗系核,记为γ。 宗系核的求解过程如下: (1)计算所有非空子联盟的联盟平均值,a(T)=V(T)/|T|; (3)找出所有宗系的联盟集合,分为纯宗系和混合宗系; (4)对于宗系联盟中的每个局中人,进一步求其准宗系联盟; (5)被瓦解的宗系联盟中的局中人,基于自身的纯宗系或准宗系,与其他宗系中的局中人进行谈判,找到可以获得最大帕累托改进的联盟进行合作,分割合作带来的剩余,由此形成博弈的宗系核。 定义6[25]宗系值。对博弈的宗系核出现的概率进行估算,然后求出宗系核的数学期望值,即为宗系值,记为χ,有χ=E(γ)。 定义7宗系解[26]。基于宗系求得的宗系核γ和宗系值χ,合称为“宗系解”。 绿色供应链中的博弈主要分为两个阶段: (1)第一阶段(非合作博弈) 本阶段是供应商和制造商做出策略选择的阶段。绿色供应链中的每个成员需明确自己的策略si∈Si(i=s,m,n,o),由此形成策略局势s∈S。即供应商选择是否共享绿色技术,制造商选择是否进行绿色技术创新。 (2)第二阶段(合作博弈) 本阶段是通过考虑预期分配的收益,明确绿色供应链的供应商和制造商的组合。利用宗系解将不同策略选择下的预期收益分配给绿色供应链成员,然后由策略局势s确定合作博弈V(s),并记绿色供应链成员的收益为(πs,πm,πn,πo)。 在由一个供应商s和三个制造商i(i=m,n,o)组成的两级绿色供应链中,供应商的策略选择与其信心指数的相关性较弱,与其共享绿色技术和制造商绿色技术创新的相关性较强,因此供应商很难根据信心指数φs进行策略选择[21]。下面的研究将不再考虑供应商的信心指数。供应商的策略集为Ss={共享绿色技术,不共享绿色技术},制造商的策略集为Si={绿色技术创新,绿色技术不创新}(i=m,n,o)。为简练符号,下文将用Si={1,0}(i=s,m,n,o)表示绿色供应链成员的策略集,其中:1表示供应商选择共享绿色技术,制造商选择绿色技术创新;0表示供应商选择不共享绿色技术,制造商选择绿色技术不创新。则供应链成员所有选择组成的策略局势如表2所示。 其中,策略局势s1=(0,0,0,0)表示供应商s选择不共享绿色技术,制造商m,n,o选择绿色技术不创新,简记为s1,其余策略局势的处理类似。借鉴BRANDENBURGER等[20]和鲁馨蔓等[31]的研究思路,本章将分两部分对它们的策略选择和收益分配进行研究。第一部分讨论策略局势s1和s9,此时不考虑制造商的绿色技术创新,只需要考虑供应商是否共享绿色技术即可;第二部分将对所有策略局势进行研究,并得出供应商和制造商的最优策略选择。 在制造商不进行绿色技术创新的基础上,本节用两型博弈模型分析供应商是否会选择共享绿色技术,以及绿色供应链成员间的收益分配。选取宗系解对绿色供应链的总收益进行预分配,即可得到绿色供应链成员的分配值,进而可以得到供应商的合作伙伴选择策略。如图1所示为该绿色供应链成员博弈的决策顺序。 图1 绿色供应链成员的决策顺序 如图2所示为局势s1和s9下绿色供应链成员博弈的决策树。由图2可知当供应商s选择不共享绿色技术时,该绿色供应链的收益区间为[min{A0,B0,D0},max{A0,B0,D0}],其中: 图2 不考虑制造商绿色技术创新时博弈决策树 A0=θmθn(pm+pn)+(1-θn)θmpm+ (2) B0=θmθo(pm+po)+(1-θo)θmpm+ (3) D0=θnθo(pn+po)+(1-θo)θnpn+ (4) 当供应商s选择共享绿色技术时,该绿色供应链的收益区间为[min{A1,B1,D1},max{A1,B1,D1}],其中: (5) (6) (7) 通过分析可得命题1。 命题1若不考虑制造商绿色技术创新,在两型博弈(Ss,Sm,Sn,So;V(s))中,用宗系解将收益值分配给绿色供应链中成员时,供应商s选择合作的制造商小联盟为mn或者mo,且合作关系成立的概率由制造商n和制造商o的安全系数决定。若θn=θo,两者成立的概率相同;若θn≠θo,供应商的选择取决于制造商安全系数的大小。具体策略选择如表3所示。 表3 宗系解下供应商的策略选择 证明不考虑制造商的绿色技术创新时,无论供应商s是否选择共享绿色技术,若θn=θo,该博弈的纯宗系联盟为{s,m,n}、{s,m,o},没有混合宗系;若θn>θo,该博弈的纯宗系联盟为{s,m,n},混合宗系联盟为{s,m,o};若θn<θo,该博弈的纯宗系联盟为{s,m,o},混合宗系联盟为{s,m,n},且3种情况下的准宗系均为个人单干的联盟。由该绿色供应链的竞合关系可知,其他联盟的特征值是不存在的,即其他联盟的特征值缺失,再结合博弈的有效联盟为{s,m,n}、{s,m,o},无效联盟为{s,n,o}和个人单干的联盟,以及本文的假设,可求得博弈的宗系核如表4所示。在不考虑其他假设情况下,θn≠θo时,宗系核和宗系值是重合的,而θn=θo时每个纯宗系出现的概率均为1/2,因此θn=θo时,该博弈的宗系值如表5所示。 表4 供应商不同策略选择下合作博弈的宗系核 表5 供应商不同策略选择下合作博弈的宗系值(θn=θo) 综上所述,在该绿色供应链中,不考虑制造商绿色技术创新的情况下,供应商s具备相当大的主导权,同时也不可低估制造商m的作用,在该博弈的宗系核和宗系值中都可以展现出s和m的重要地位。而制造商n和o受竞合关系和安全系数的限制,可以认为其处于被动的地位,宗系核表明两个制造商中只能有一个参加合作,宗系值表明二者的地位取决于安全系数,当θn=θo时,两者地位无差异且合作发生的概率都是1/2;当θn≠θo时,两者地位的差异和合作发生的概率都与安全系数的大小有关。 在制造商进行绿色技术创新的基础上,本节用两型博弈模型分析供应商是否会选择共享绿色技术,以及绿色供应链成员间的收益分配。选取宗系解对绿色供应链的总收益进行预分配,即可得到绿色供应链成员的分配值,进而可以得到供应商的合作伙伴选择策略。如图3所示为该绿色供应链成员博弈的决策顺序。 图3 绿色供应链成员的决策顺序 如图4所示为表2中所有策略局势下绿色供应链成员博弈的决策树。由图4可知,当供应商s选择不共享技术时,该绿色供应链的收益区间为[min{X0,Y0,Z0},max{X0,Y0,Z0}],其中: 图4 考虑制造商绿色技术创新时博弈决策树 X0=A0+θmUm+θnUn; (8) Y0=B0+θmUm+θoUo; (9) Z0=D0+θnUn+θoUo。 (10) 当供应商s选择技术共享时,该绿色供应链的收益区间为[min{X1,Y1,Z1},max{X1,Y1,Z1}],其中: X1=A1+θmUm+θnUn; (11) Y1=B1+θmUm+θoUo; (12) Z1=D1+θnUn+θoUo。 (13) 通过分析可得命题2。 命题2若考虑制造商绿色技术创新,在两型博弈(Ss,Sm,Sn,So;V(s))中,用宗系解将收益值分配给绿色供应链中成员时,供应商s在θn=θo和θn≠θo时的策略选择是有差异的,但分析方法同理。若θn=θo,分析所得有效纳什均衡、绿色供应链合作联盟以及制造商进行绿色技术创新的投入量如表6所示。 表6 宗系解下绿色供应链成员的策略选择(θn=θo) 证明该命题的证明由以下3个部分构成: (1)在供应商s选择不共享绿色技术,考虑制造商绿色技术创新的情况下,用宗系解分配绿色供应链成员在8种策略局势(即局势s1~s8)下的预期收益。当Un>Uo且θmpm-θopo<θoUo-θmUm或Un 表7 供应商不共享技术时制造商的预期收益 表8 供应商共享技术时制造商的预期收益 (3)将上述6种情况归纳为图5,通过对比所示的6种情况下供应商的预期收益值,可以得到绿色供应链合作伙伴选择的最优策略。如在cs>(θntβspn)2且Un>Uo且θmpm-θopo>θoUo-θmUm的条件下,供应商的最优策略是不共享绿色技术,并选择制造商m和n为合作伙伴组成绿色供应链{s,m,n}。 图5 考虑制造商绿色技术创新时供应商的预期收益 通过上述分析可以看出,当考虑制造商进行绿色技术创新时,无论供应商是否共享绿色技术,只有在制造商n和o所创效益较高时,供应商才会选择与其组成绿色供应链。其他情况下,供应商对于组成绿色供应链的合作伙伴则是制造商m和n,或者是制造商m和o。被供应商选择的合作伙伴会选择绿色技术创新且最优绿色技术创新投入量分别为δi(i=m,n,o)。综上可得表6,命题2得证。 (1)当制造商不进行绿色技术创新,分析供应商共享绿色技术时的预期收益变化趋势如图6所示。绿色供应链中合作联盟的纯宗系会根据安全系数θn与θo的大小改变,当θn=θo时,绿色供应链中的纯宗系联盟为T1={s,m,n}和T2={s,m,o},且出现的概率相同;当θn≠θo时,绿色供应链中的纯宗系联盟为T1或T2,且出现的概率与θn和θo成正相关。在此情况下,绿色供应链T3={s,n,o}的预期总收益会低于绿色供应链T1或T2的预期总收益,相应的也会限制供应商共享绿色技术的投入成本,且只有成本较低时才会选择共享绿色技术。 假设θn=θo=0.81,由宗系解可知供应商在不同共享绿色技术选择下的预期收益关系如图6a所示。无论供应商是否选择共享绿色技术,在无其他因素影响的情况下,纯宗系联盟T1={s,m,n}和T2={s,m,o}总是以相同的概率出现。当cs<3.7791时,供应商选择共享绿色技术,最优的共享成本为cs=0.9448,相应的收益是4.9349;当cs≥3.7791时,供应商选择不共享绿色技术,相应的收益是4.62。因此,当供应商以成本cs=0.9448共享绿色技术时,其收益可达到最大值。这是由于制造商n和o的安全系数低于制造商m,即两者在绿色供应链的稳定性方面会弱于制造商m,从而导致绿色供应链T3的预期收益低于绿色供应链T1和T2。当供应商受其他因素影响选择组建绿色供应链T3时,若制造商n和o不能积极主动提高自身的优势,获得更多的效益,也会减弱供应商在该绿色供应链中选择共享绿色技术的积极性,因此供应商在综合考量的前提下组建绿色供应链T3的可能性较低。在θn=0.81,θo=0.72时,由宗系解可知供应商在不同共享绿色技术选择下的预期收益关系如图6b所示,分析过程与θn=θo相似,故不再赘述。 (2)当制造商进行绿色技术创新,假设Um=3,Un=Uo=4.2,在制造商成员n和o的绿色技术创新预期效用都高于制造商成员m的情况下,分析供应商共享绿色技术时的预期收益变化趋势如图7所示。令θn=θo=0.81,由宗系解可知供应商在不同共享绿色技术选择下的预期收益关系如图7a所示。当cs<6.3793时,供应商选择共享绿色技术,其中cs<3.1277时,组成的绿色供应链联盟为T1或T2,最优的共享成本为cs=0.9448,相应的收益是6.9689;当cs=3.1277时,绿色供应链联盟T1、T2和T3均为纯宗系,且其出现的概率相同,无论供应商的选择是组成哪一个联盟,其相应的收益均为6.7547;当3.1277 基于绿色供应链收益最大化原则,在制造商成员n和o的预期创新收益都高于制造商成员m,同时供应商共享绿色技术成本投入较少的情形下,依然是绿色供应链T1和T2获得的总收益最高。这是由于制造商成员m的自身实力雄厚,即使它带来的预期创新收益较少,供应商依然会选择组建绿色供应链T1或T2并对其共享绿色技术,且在面对创新风险时,成员之间更倾向于“强强联合”,合作双方看中的往往是对方的本身实力,而非其预期创新收益。在θn=0.81,θo=0.72时,由宗系解可知供应商在不同共享绿色技术选择下的预期收益关系如图7b所示,分析过程与θn=θo相似,故不再赘述。 (3)当制造商进行绿色技术创新,假设Um=3,Un=4.2>Uo=3.9,在制造商成员n和o的绿色技术创新预期效用都高于制造商成员m的情况下,分析供应商共享绿色技术时的预期收益变化趋势如图8所示。令θn=θo=0.81,由宗系解可知供应商在不同共享绿色技术选择下的预期收益关系如图8a所示。当cs<4.9695时,供应商选择共享绿色技术,其中cs<3.5854时,组成的绿色供应链联盟为T1,最优的共享成本为cs=0.9448,相应的收益是6.9689;当cs=3.5845时,绿色供应链联盟T1和T3均为纯宗系,且其出现的概率相同,其相应的收益为6.6859;当3.5845 aθn=θo bθn≠θo 绿色技术的创新与发展是绿色供应链管理的重要内容之一,对“天下无废、负碳生态”目标的实现具有重要意义,因此对于由1个供应商和3个制造商组成的两级绿色供应链,本文使用两型博弈模型从供应商的共享绿色技术和制造商的绿色技术创新两个视角研究了它们的策略对绿色供应链预期收益分配的影响,在合作博弈阶段用宗系解分配绿色供应链合作联盟的收益,并在非合作博弈阶段得到供应商和制造商的决策。得到以下研究结果: (1)在不考虑制造商绿色技术创新的情况下,无论供应商选择共享绿色技术与否,供应商优先合作对象为能力强、基础利润高的制造商,其次根据安全系数的大小选择一个相对较优的制造商构成绿色供应链;进一步地,供应商只有在共享绿色技术成本较低时才会选择共享从而增加收益。 (2)在考虑制造商绿色技术创新的情况下,能力较强的制造商依然具备加入绿色供应链的优势,而对于相对能力较差的供应商,只有在其绿色技术创新收益高于能力较强的制造商时,才能被选中从而组成绿色供应链;且只有和供应商组成绿色供应链的制造商才会进行绿色技术创新投入。 基于以上研究结论,可以得到如下绿色供应链管理的启示: (1)企业需要积极将环保思想纳入供应链管理与合作伙伴选择决策,且对于目前绿色集成度较优的企业,不妨在供应链上下游合作中给予其他企业支持以提高整个供应链的绿色化程度,这也是实现供应链协作的重要途径。 (2)绿色技术创新的效果是明显的,企业应积极推动技术创新活动的开展,借助技术创新撬开环保、经济两扇大门,展现其积极效用。 (3)企业的技术创新活动不仅可以提升自身在合作关系中的竞争力,还可以在面对新挑战的时候有更深厚的底气,才能在时代的进步中更好发展,而且现行政策对中小型企业技术创新的支持也可以在一定程度上减少其风险,这些都是促进企业绿色创新的动力。 但是本文的研究还存在一定的局限和不足,首先,未考虑到中断风险的应对措施,如受公共突发事件的影响导致供应链中断时,政府会进行宏观调控;其次,在实际市场环境中,多个供应商和多个制造商或零售商相互竞争的情况更普遍,本文未涉及到多企业合作的决策与收益分配问题,在后续的研究中可以进一步探索。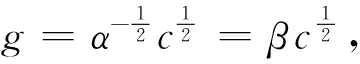
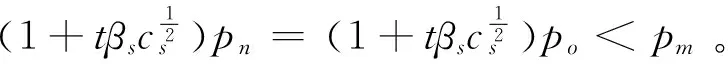
2.2 两型博弈模型
2.3 宗系解
3 绿色供应链中的两型博弈模型

3.1 不考虑制造商绿色技术创新的两型博弈模型

(1-θm)θnpn=θmpm+θnpn;
(1-θm)θopo=θmpm+θopo;
(1-θn)θopo=θnpn+θopo。

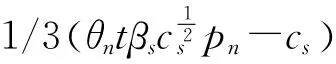
3.2 考虑制造商绿色技术创新的两型博弈模型


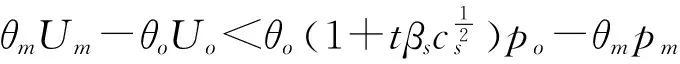
4 数值算例
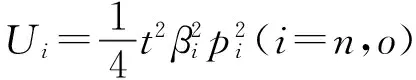
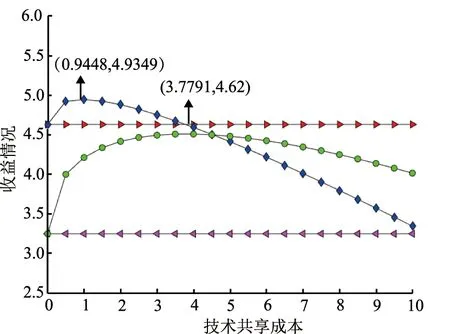

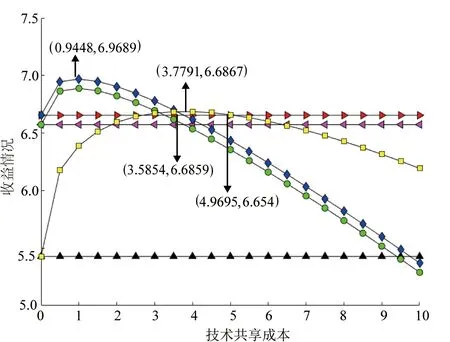

图8 考虑制造商绿色技术创新且Un>Uo时供应商的预期收益5 结束语
