面向无人机通信安全的波束成形策略研究

马晓琳，袁全盛，江 源，王长龙

（1.陆军工程大学石家庄校区 无人机工程系，河北 石家庄 050003；2.桂林联勤保障中心，广西 桂林 541004；3.中国人民解放军32382 部队，湖北 武汉 430311）

0 引言

近年来，随着无人机技术的发展，无人机在未来战场中的通信侦察、监控搜索、实时打击等方面将扮演重要角色[1-2]。然而，由于无人机通信信道属于无线信道，使得敏感信息常常暴露在敌方的视野中，这使得无人机通信的数据安全受到严峻的威胁。当前的装备通信安全方法一般采用密钥通信，这种安全通信方法在无人机通信中存在以下不足：

1）基于密码学的加密解密系统严重依赖于通信双方的计算能力，储存、管理、分发长秘钥将大大降低无人机的续航能力和任务效能，增大无人机空地通信延迟；

2）无人机信道具有开放性、随机性、衰落性的特点，使得基于网络层及以上各层应用的密码学技术在无人机通信中的应用存在困难；

3）随着计算机技术的发展，密码破解技术随之不断进步，基于密码学的加密解密系统存在安全隐患。

结合无人机通信的具体特点，利用无线信道的物理特性实现安全通信的物理层安全技术可以为无人机战场通信提供安全保障。物理层安全技术作为传统加密技术的补充，利用合法信道与窃听信道之间的质量差异实现安全通信[3]，近年来受到广泛关注。将物理层安全技术用于无人机通信中，可在提高安全性的同时降低加密复杂度，节省计算资源[4-5]。

目前，大部分有关物理层安全技术的研究假设合法信道与窃听信道的信道状态信息（Channel State Information,CSI）均是准确可知的[6-7]，但在实际通信环境中，无人机很难获取准确的窃听信道CSI，只能通过无人机上的光电设备或合成孔径雷达等获取窃听节点的位置信息[8]。目前，物理层波束成形技术可显著提高通信系统的物理层安全性能，但一般都是二维设计，即固定垂直方向波束成形角[9-10]，但实际的无人机通信模型具有三维空间特性，这意味着二维波束成形技术不是最优波束成形方案。

为此，本文提出基于位置信息的三维波束成形技术，增加了信息传输中的安全自由度，并给出了系统安全中断概率的表达式；提出波束成形向量和无人机路径规划联合优化算法，进一步提高无人机空对地通信的物理层安全性能。

1 系统模型

在笛卡尔坐标系下，三维无人机空对地无线通信模型如图1 所示。

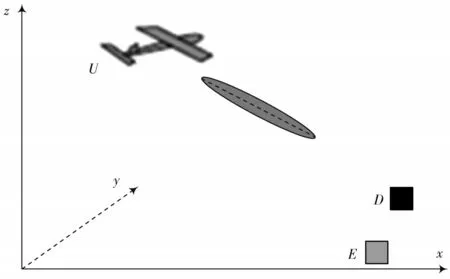
图1 无人机空对地通信模型

图1 中：U为无人机；D为目的节点；E为窃听节点；目的节点的坐标为(xD,yD,0)；窃听节点的坐标为(xE,yE,0)；无人机的时变坐标为(xU(t),yU(t),H)，0 ≤t≤T，T为飞行时间，H为飞行高度。将T分成N个相等的时隙Ts，即T=NTs，设Ts足够小，且无人机在每个时隙内的位置固定不变，则无人机的坐标可表示为。若无人机飞行速度v恒定，且主飞行方向为x轴，即无人机的航向偏离x轴的角度σU[n]∈(-π 2,π 2)。

无人机和目的节点之间的信道称为合法信道，无人机和窃听节点之间的信道称为窃听信道。假设无人机可知合法信道的CSI，但是无法获取窃听信道的CSI，仅可通过无人机上的光学相机或者合成孔径雷达得知窃听节点的位置信息。无人机配备均匀线性阵列（Uniform Linear Array,ULA）天线或者均匀圆形阵列（Uniform Circular Array,UCA）天线，天线数目为NU，目的节点和窃听节点均为单天线设备，目的节点和窃听节点采用最大比合并（Maximal-Ratio-Combining,MRC）技术接收信号。

基于以上假设，定义yi[n],i∈{D,E}为目的节点（i=D）或窃听节点（i=E）在第n时隙接收到的信号，yi[n]可表示为：

式中：P为无人机的发送功率；为第n时隙的合法信道系数或窃听信道系数；b[n]为第n时隙的波束成形向量；s[n]为第n时隙无人机发送的信号；zi[n]表示第n时隙目的节点或窃听节点处的加性高斯噪声，且zi[n]～CN(0,)；Li[n]表示路径衰落。

Li[n]可表示为[11]：

式中：di[n]为第n时隙无人机到目的节点或窃听节点之间的距离；β0为参考距离处的信道功率；ηi为合法信道或窃听信道路径损耗因子。

为准确刻画基于位置信息的无人机空对地信道小尺度衰落特征，采用莱斯衰落信道，则hi[n]可以表示为：

式中：Ki[n]为合法信道或窃听信道的莱斯因子；hi,L[n]为hi[n]的视距部分；hi,N[n]为hi[n]的非视距部分且服从零均值循环对称复高斯分布，即hi,N[n]～CN(0,INU)。

根据文献[12-13]，无人机空对地莱斯衰落信道中的莱斯因子以及路径损耗因子是仰角的函数，可表示为：

式中：ϑi[n]为第n时隙目的节点或窃听节点到无人机的仰角；α1、α2、α3、β1、β2、β3为环境频率依赖常数。

无人机天线为ULA 时，hi,L[n]可以表示为[14]：

式中：τ=2πλ，λ为信号波长；ρU为无人机处天线阵元间距；αi[n]为第n时隙信号从无人机到目的节点或窃听节点的水平发射角；ζi[n]为第n时隙信号从无人机到目的节点或窃听节点的垂直发射角。

无人机天线为UCA 时，hi,L[n]可以表示为[14]：

2 安全中断概率

用γi[n],i∈{D,E}表示第n时隙目的节点（i=D）或窃听节点（i=E）处的接收信噪比，γi[n]可以表示为：

因为合法信道CSI 已知，则可通过计算直接得到γD[n]。为求得安全中断概率，需要求得γE[n]的概率密度函数（Probability Density Function,PDF）fγE[n](γ)。

首先分析‖hE[n]b[n]‖的分布类型，根据式（1）可得：

莱斯随机变量的概率密度函数包含第一类零阶修正Bessel 函数，不利于进一步分析。莱斯分布是Nakagami 分布的一种特殊情形，因此可将该莱斯分布转化为Nakagami 分布，其参数为：

根据文献[15]，fγE[n](γ)可表示为：

式中Γ(x)为Gamma 函数。

当γD[n]≤γE[n]时，系统无法实现安全通信，则系统可达安全速率为零；当γD[n]＞γE[n]时，定义可达安全速率为合法信道可达速率与窃听信道可达速率的差。因此，系统第n时隙的可达安全速率CS[n]可以表示为[16]：

式中：CD[n]=log2(1 +γD[n])为第n时隙的合法信道可达速率；CE[n]=log2(1 +γE[n])为第n时隙的窃听信道可达速率。定义设定的安全传输速率为Rth，那么当CS[n]≥Rth时，实现无人机空对地安全通信；当CS[n]＜Rth时，无法保证无人机空对地通信安全，发生安全中断。

因此，定义安全中断概率为：

定理1：当合法信道CSI 已知，窃听信道CSI 未知时，基于三维波束成形的无人机空对地通信系统的安全中断概率为：

式中Γ(α,x)为上不完全Gamma 函数。

证明：由式（15）和式（16）可得：

将式（14）代入式（18），可得：

其中最后一个步骤根据文献[17]中的结论可得。

定理1 得证。

3 传输方案设计

本文考虑联合设计波束成形向量和无人机航迹以最小化安全中断概率的优化问题。假设无人机的初始位置为(0,0,H)，无人机向前飞行且飞行在一定范围内，则该优化问题具有位置约束。此外，因为无人机以恒定速度v飞行，则该优化问题具有速度约束。将安全中断概率表示为Ps[n]，则安全中断概率最小化优化问题可以描述为：

考虑到问题P1 是一个非凸优化问题，将其分解为2 个子问题，即固定路径下的波束成形向量优化问题和固定波束成形向量下的路径规划问题，并分别求出2 个子问题的解。然后，基于2 个子问题的优化算法，提出联合优化算法以解决问题P1。

3.1 波束成形向量优化

假设无人机路径固定，则此时的波束成形向量优化问题可以表示为：

问题P2 除了是问题P1 的子问题以外，还对应现实场景中无人机在执行某些任务时需要预先确定路径的情形。

定理2：定义波束成形向量系数τ∈[0,1]，则问题P2 的解为：

因为θ1和θ2的取值对γD[n]和γE[n]没有影响，为表示方便，取θ1=θ2=0。

定理2 得证。

根据上述分析，给出波束成形向量优化算法如下：

初始化：输入系统模型参数。

1：根据式（24）、式（25）计算b1[n]和b2[n]

2：for 对τ∈[0,1]以步长τt执行

3：根据式（23）计算波束成形向量b[n](τ)

4：根据式（18）计算安全中断概率Ps(Rth)[n]

5：end for

6：选择使得Ps(Rth)[n]最小的τ作为最优波束成形向量系数τ*，输出最优波束成形向量b[n](τ*)

路径规划算法如下：

3.2 无人机路径规划

假设无人机波束成形向量固定，则此时的无人机路径规划问题可以表示为：

为解决问题P3，假设x[n]=x[n-1]+ε[n]，y[n]=y[n-1]+δ[n]，其中{ε[n],δ[n]} 表示第n时隙无人机在x轴方向和y轴方向上的路径增量，则问题P3 可以转化为：

因为无人机的航向角σU[n]∈(-π 2,π 2)，则无人机在第n时隙的位置总位于以无人机第n-1 时隙的位置为圆心、以vTs为半径的半圆上，因此求解问题P4 可以转化为在位置约束下寻求最优的航向角[n]∈(-π 2,π 2)，以使得安全中断概率Ps(Rth)[n]最小化。通过路径规划算法可将二维优化问题转化为一维优化问题，显著提高优化效率。

3.3 联合优化算法

基于波束成形向量优化算法和路径规划算法，提出迭代联合优化算法解决问题P1，以最小化系统安全中断概率。

联合优化算法如下：

初始化：输入系统模型参数。

1：Repeat

2：根据波束成形向量优化算法得到第n时隙的最优波束成形向量b[n]

3：根据路径规划算法得到第n+1 时隙的无人机最优坐标

4：n→n+1

5：输出无人机最优路径{xU[n],yU[n]} 以及对应坐标的最优波束成形向量

4 数值分析

本节利用蒙特卡罗仿真对系统安全中断概率进行分析，并与理论推导进行比较，验证所给出的中断概率表达式的准确性。所有仿真值均是通过104次实验取平均值。

在系统模型中，无人机定高匀速飞行，其飞行高度H=400 m，飞行速度v=60 km/h，飞行距离=2 km，目的节点位于（2 000,0,0）m，窃听节点位于（1 000,500,0）m。无人机的发射功率为10 dBm，目的节点和窃听节点处的噪声功率均为-169 dBm，时隙Ts=1 ms，给定的私密信息传输速率Rth=3 bit/s/Hz。

图2 给出了无人机配备天线为ULA 时，所提算法与其他3 种参考策略的安全中断概率曲线。

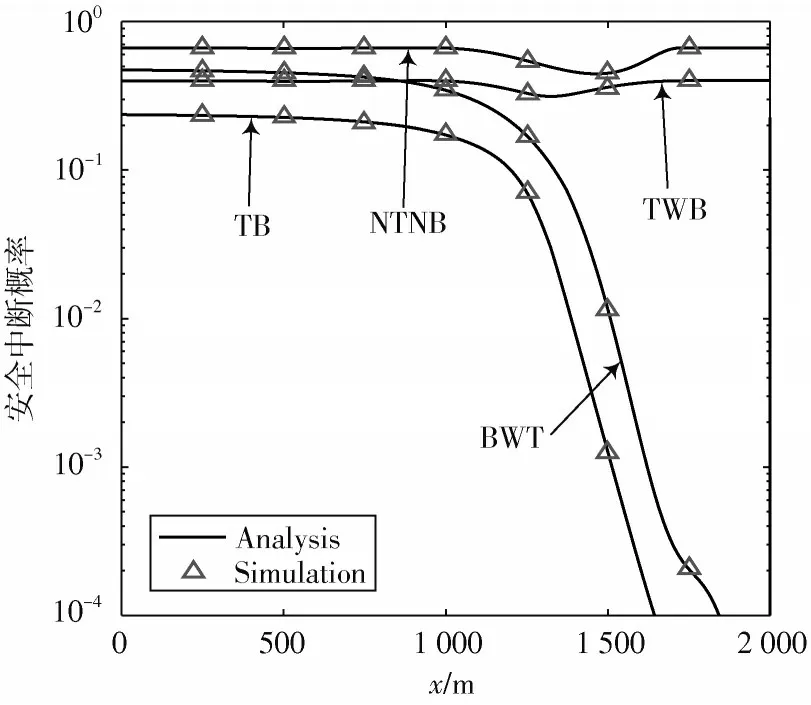
图2 无人机配备天线为ULA 时系统安全中断概率

图3 给出了无人机配备天线为UCA 时，所提算法与其他3 种参考策略的安全中断概率曲线。

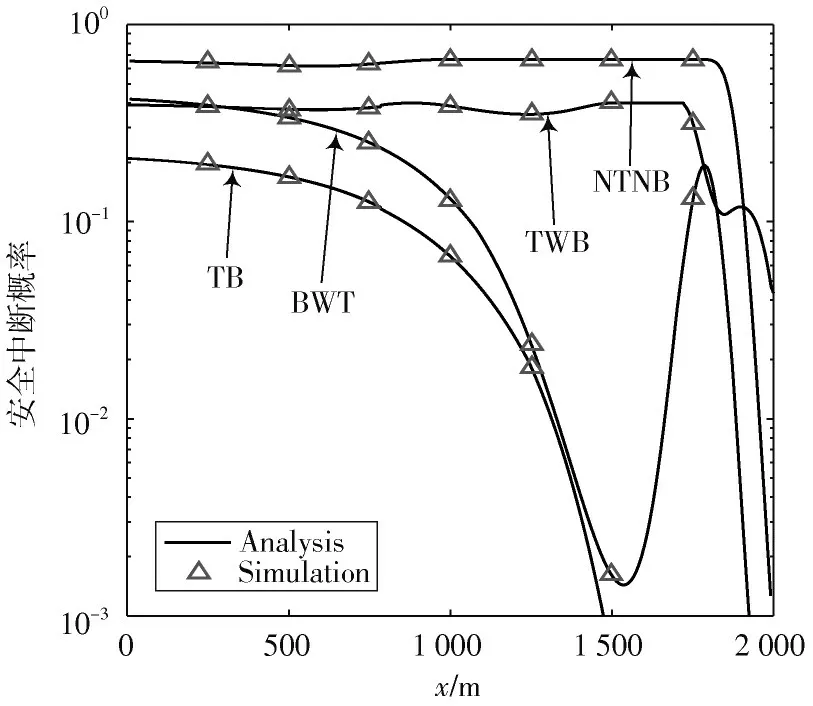
图3 无人机配备天线为UCA 时系统安全中断概率

图中：NTNB 表示未进行波束成形向量优化和路径规划；BWT 表示进行波束成形向量优化但是未进行路径规划；TWB 表示进行了路径规划但是未进行波束成形向量优化；TB 表示联合优化了波束成形向量和无人机飞行路径。

从图2、图3 中可以看出：

1）蒙特卡罗仿真结果与理论推导结果高度相符，验证了定理1 的准确性；

2）所提算法明显提高了系统安全中断性能；

3）随着无人机逐渐靠近目的节点，所有方案的安全中断概率降低，因为合法信道质量提高，安全性能改善；

4）无人机配备天线为ULA 时系统安全性能较好。

图4 给出了不同天线数目下的系统安全中断概率曲线。

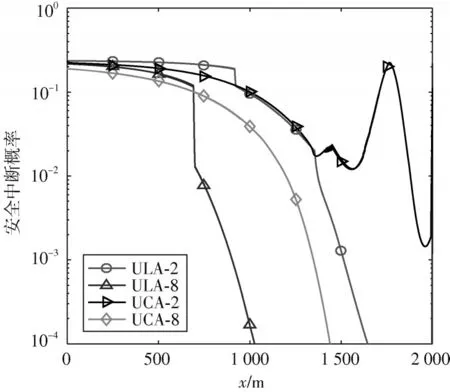
图4 Rayleigh 衰落环境下节点A 处的中断概率

由图4 可以看出：

1）随着无人机天线数目的增加，系统的安全中断概率下降，系统安全性能提高；

2）无人机天线数目较少时，配备ULA 或者UCA 天线的系统安全性能差距较小，随着天线数目的增加，二者性能差距增大；

3）采用ULA 天线配置的系统安全性能总体优于UCA 配置时的性能。

图5 为图4 中不同天线数目下的无人机航迹曲线，可以看出，为提高系统安全性能，经过路径规划后，无人机往远离窃听者的方向飞行。

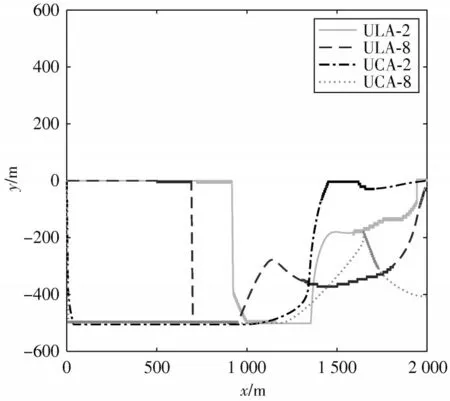
图5 不同天线数目下的无人机航迹

5 结论

本文在假设无人机无法获取窃听信道的信道状态信息的前提下，为提高系统安全性能，基于无人机三维通信模型，提出基于位置信息的三维波束成形技术，分析了系统参数对安全性能的影响，实现了无人机通信安全传输策略的动态调整，为无人机通信安全传输方案优化设计提供了理论依据。但本文仅分析了系统中只有一个无人机和一个地面目标节点的情况，对于多无人机和多目标通信系统的三维波束成形技术还有待进一步研究。