基于HL-MAD组合估计量的常规控制图稳健改进
2023-10-10李熠玲任凯亮王志坚
李熠玲,任凯亮,王志坚*
(1.广东财经大学统计与数学学院,广东 广州 510320;2.康涅狄格大学文理学院,美国 康涅狄格州 06268)
1 引言
统计过程控制是一项建立在数理统计学原理基础之上的过程质量管理技术。从诞生至今,经过近100年的发展与完善,统计过程控制技术已经被广泛应用于社会经济发展的各个领域,包括物流、数字经济、服务业等,取得了良好的社会和经济效益,其监控的过程也从传统单变量过程拓展到各种多变量场景。而在实际工作中,控制图则是常被用来对受控过程进行质量管理的工具之一,通过使用控制图,能够对过程绩效及其波动原因进行直观而实时的监控和分析,帮助人们及早地发现和识别异常现象并找出异常原因,从而提高产品或服务质量。
质量控制图的基本原理主要包含以下四个方面:受控过程服从正态分布的假定;控制限的准则;在一次试验中小概率事件不发生的原理;数理统计学中的统计推断基本思想。
受控过程的正态性假定是指受控过程在正常状态下,其相关的特性指标数据服从正态分布假定。控制限的准则是指当某个过程特性数据服从正态分布N(μ,σ2)时,可以利用正态分布的3σ准则得出控制图的设计原理即控制上限UCL=,控制中心线CL=^μ,控制下限LCL=。小概率事件不发生原理是指在一次观测试验中,正常情况下小概率事件通常认为不发生。统计推断的基本思想认为,若在过程控制中一旦出现了“小概率事件发生”的现象,则可以认为受控过程出现异常。
同时,应注意到,一方面,统计过程控制技术的理论基础之一,控制限的准则即为常规控制图的控制设计原理,其中控制上限UCL=、控制中心线CL=、控制下限LCL=所采用的统计量,均值与标准差σ^对离群值敏感,缺乏稳健性;另一方面,在离群值存在时,过程质量特性数据很难满足正态分布假定。因此,常规控制图在对过程异常情况识别时,易受离群值干扰,常出现“遮蔽效应”或“漏报警”现象,从而极大地降低了控制图监测性能,如何解决此类问题即是本研究的出发点。
2 文献综述
近20年,稳健统计技术在各领域的过程控制中应用越来越多,包括经济、金融、工业制造、服务业等。刚开始多是对单变量控制图采用不同的稳健方法进行设计,如均值Xbar控制图。维贾雅(Vijaya)和墨蒂(Murty)[1]讨论了采用基于风险的方法来找到Xbar控制图的最佳参数对Xbar控制图进行稳健经济设计。周纯光等[2]提出了一种基于小波的预分析稳健控制图,用于监测第一阶段过程控制中的均值漂移。吴纯杰和王兆军[3]分析了休哈特Xbar控制图的不稳健性,并对其进行了稳健修正。阿卜秋勒(Abdul)等[4]研究了利用考虑不确定参数区间估计的稳健优化方法进行Xbar控制图的经济统计设计(ESD),开发了一种启发式算法来获得控制图的稳健方案,效果优于传统ESD。萨利赫(Salih)等[5]对因素选择控制图的最优稳健设计进行了研究。
随后,越来越多的学者开始关注多变量控制图的稳健性。哈布沙(Habshah)和阿什坎(Ashkan)[6]提出了稳健多元CUSUM 图和多元EWMA图,以解决散点异常值变化小的问题。范(Fan)等[7]基于分层聚类树原理开发了一种新的稳健多变量控制图,该图可以有效地检测多维数据中的潜在异常值,同时控制遮蔽和淹没效应。阿索坎(Asokan)和贾亚尚卡尔(Jayasankar)[8]提出了监测第一阶段多变量个体观测过程均值的稳健控制图。张(Zhang)等[9]提出了一种无分布的多变量统计过程控制图(MSPC),以检测多变量过程变量的一般分布变化。安杰尼丝(Angellys)等[10]将截尾均值应用于稳健多变量控制图的异常值诊断。拉吉(Raji)等[11]基于Stahel Donoho稳健估计量(SDRE)构建了一种稳健多变量控制图,同时从第一阶段估计过程参数。卡丽纳(Cabana)和利洛(Lillo)[12]基于稳健重加权收缩估计,提出了一种用于个体观测的稳健多变量质量控制技术。萨巴诺(Sabahno)和塞拉诺(Celano)[13]用可变参数控制图监测存在自相关的多变量变异系数。
近年来,也有学者研究自相关过程残差控制图的稳健性。王志坚[14]通过权重函数对ARMA 模型与GARCH 模型进行稳健建模,最后构建稳健残差控制图。王志坚等[15-16]通过构建稳健AR 模型,为自相关过程残差控制图的设计提供了理论依据。萨里阿提(Shariati)[17]提出了一种适用于自相关序列的稳健控制图新方法,该图对污染数据的影响具有稳健性。萨拉赫(Salah)等[18]研究了伽马回归模型下残差控制图的剖面监测。
通过梳理文献发现,不少学者从控制图控制限的位置参数、尺度参数角度采用稳健估计量来构建稳健控制图。哈菲兹(Hafiz)等[19]建立了稳健Shewhart位置参数控制特征的逐步筛选方法。纳迪娅(Nadia)和沙希德(Shahid)[20]比较了文献中的六种不同稳健尺度估计下的EWMA 控制图性能,模拟研究结果表明,基于估计量Q_n的控制图在非正常过程中表现相对较好。吴纯杰等[21]、庄芳等[22]分别分析了稳健似然比累积和控制图及EWMA 方差控制图的不稳健性,并给出了稳健改进的方法。王志坚、苏拥英等[23-24]对常规过程控制图的敏感性进行了分析并给出了稳健化方法。卡奥(Kao)[25]认为,当存在污染数据时,标准偏差的估计会由于其高偏差性而降低控制图的检测能力,于是提出了基于不同筛选的平方A 估计量,该估计量在抗干扰方面表现相对最好。
与前人不同的是,本研究尝试采用估计量Hodges-Lehmann(简写HL)与中位绝对离差(MAD)相结合的方式对常规控制图控制中心及控制限进行稳健改进,并通过改进前后对比的研究方法验证稳健控制图的可行性和有效性。
3 相关理论与方法
3.1 常规控制图的不稳健性研究
常规休哈特控制图设计原理,主要包括控制中心、上下控制限,相应表达式如(1)式所示:
(1)式中的k通常取3,显然UCL、CL、LCL 所采用的统计量缺乏稳健性,导致整个控制图对离群值过于敏感,当受控过程出现异常情况时会使得控制中心、控制限的值不能反映大多数样本数据的特征,因此控制图常会出现“漏报警”现象。
接下来通过举例论证在对异常现象监控时常规控制图如何“失控”。先采用R 软件生成20个服从N(0,1)分布的随机数作为过程的特性指标数据,再通过随机抽样技术在20个随机数里面随机抽取一个数用4.5去代替之,我们将4.5作为20个随机数里面的异常值。接下来基于不含异常值及含1个异常值的序列构建两个常规控制图,第一个是不含异常值常规控制图,第二个是含1个异常值常规控制图,两个控制图的监测结果如图1所示。
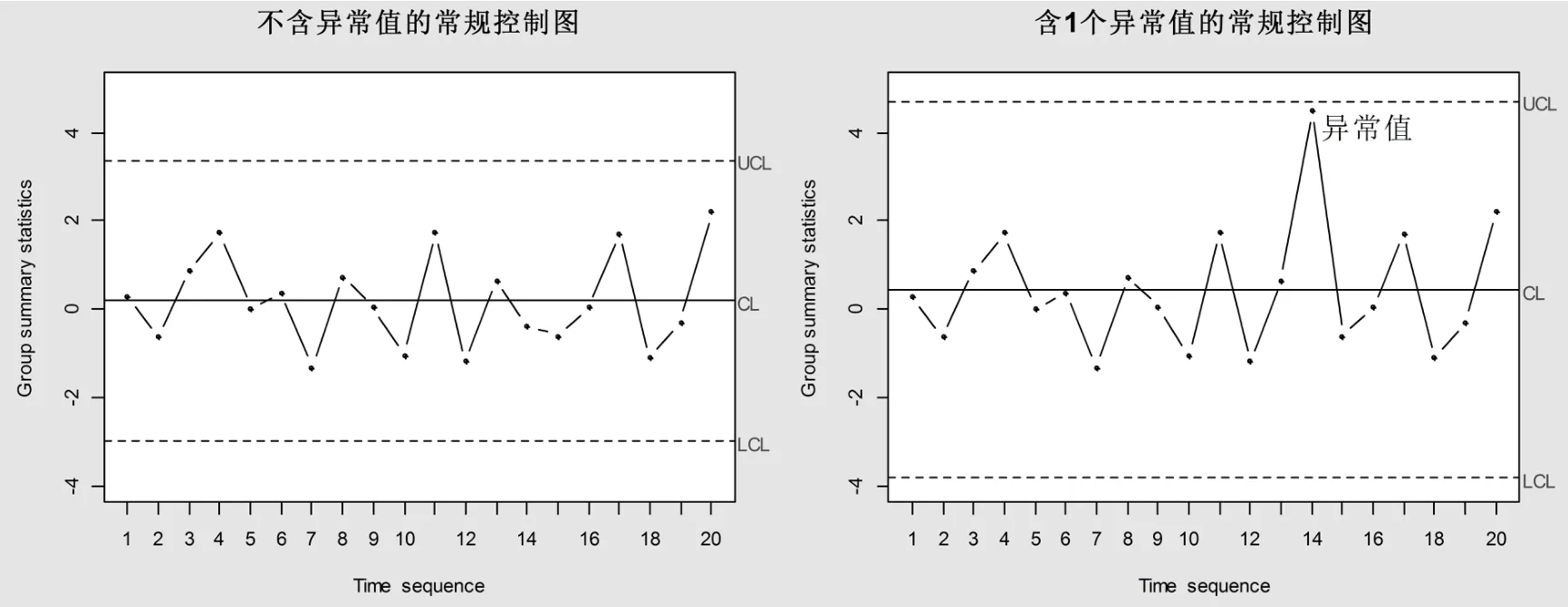
图1 不含异常值的常规控制图(左)与含1个异常值的常规控制图(右)
从图1可以看出,两个控制图的中间实线为控制中心线,上下两条虚线为控制上下限。由于图1左图中的受控过程不含异常值,所有的点均在上下控制限以内,没有出现“虚假报警”或者“漏报警”现象,监控成功。而图1右图中的受控过程含有一个异常值,但从图1右图中可以看出,异常值在上下控制限内,控制图并没有对异常值进行报警,而是将异常值误判正常值,监控失败。显然,监控失败的原因是由于控制限对异常值敏感,异常值的存在导致控制上下限间距拉大所致。因此,对常规控制图的控制中心及控制限进行稳健改进具有重要意义。
3.2 稳健常规控制图构建的基本原理
寻找均值、标准差的稳健组合估计量来改进控制中心及控制限,对构造稳健控制图具有重要作用。研究表明构建稳健控制图是一个较为复杂的系统工作,并不是仅仅寻找均值与标准差的稳健估计量。由于均值与标准差在控制图中是有机整体,若将两者分开研究有可能会导致控制图过于稳健或者缺乏稳健,其后果是:过于稳健会出现虚假报警,缺乏稳健会出现漏报警现象。常用的均值稳健估计量有:中位数(Median)、切尾均值(Trimmed Mean)、缩尾均值(Winsorized Mean)、三均值(Triple Mean)以及Hodges-Lehmann(HL1、HL2、HL3)等。常用的标准差稳健估计量有:缩尾标准差(WSD)、中位绝对离差(Median absolute deviation)、平均绝对离差(Mean absolute deviation)、四分位数间距(IQR)以及Shamos估计量等。
本研究经过反复模拟实验比较后,采用昌世凯(Chanseok)等[26]提出的Hodges-Lehmann估计量作为均值稳健估计量,选取中位绝对离差(MAD)作为标准差稳健估计量,该两个估计量组合在一起,称为HLMAD 组合估计量。研究表明,采用该组合估计量来稳健改进常规控制图能得到相对最优的稳健监测效果。Hodges-Lehmann估计量具有3种形式,可分别简写为HL1、HL2及HL3,其表达式分别为:
在此,经比较后选HL1,其中位绝对离差(MAD)表达式为:
将该两个估计量作为控制图的稳健组合估计量来改进控制中心与控制限,可得到如下稳健控制图(图2):

图2 基于HL-MAD 组合估计量的稳健常规控制图构建原理
3.3 模拟研究
下面通过数值模拟仿真研究来说明稳健改进的可行性和有效性。分别模拟随机产生样本量为20、100、200的标准正态分布N(0,1)随机数,目的是从小样本、中样本和大样本三种情形来观测改进效果。三种情形的污染率分别为2%、10%、20%,即分别覆盖轻污染、中污染、重污染。需要说明的是,在小样本20的情形下,当污染率为2%时,异常值不足1个,为保证各样本量、各污染率下至少有1个异常值,本研究将小样本20的轻污染率由原来的2%增加到5%,其他情形不变。污染分布选择均匀分布,污染分布构造过程如(2)式所示:
其中ε为污染率,N(n1;0,1)表示标准正态分布,Unif(n2;4,5)表示最小值为4、最大值为5的均匀分布。根据研究需要,有时要产生负异常值,这时可将污染分布(2)式变形为(3)式:
基于(2)式和(3)式产生的随机数,得到各样本量、各污染率下的监控效果如表1所示。
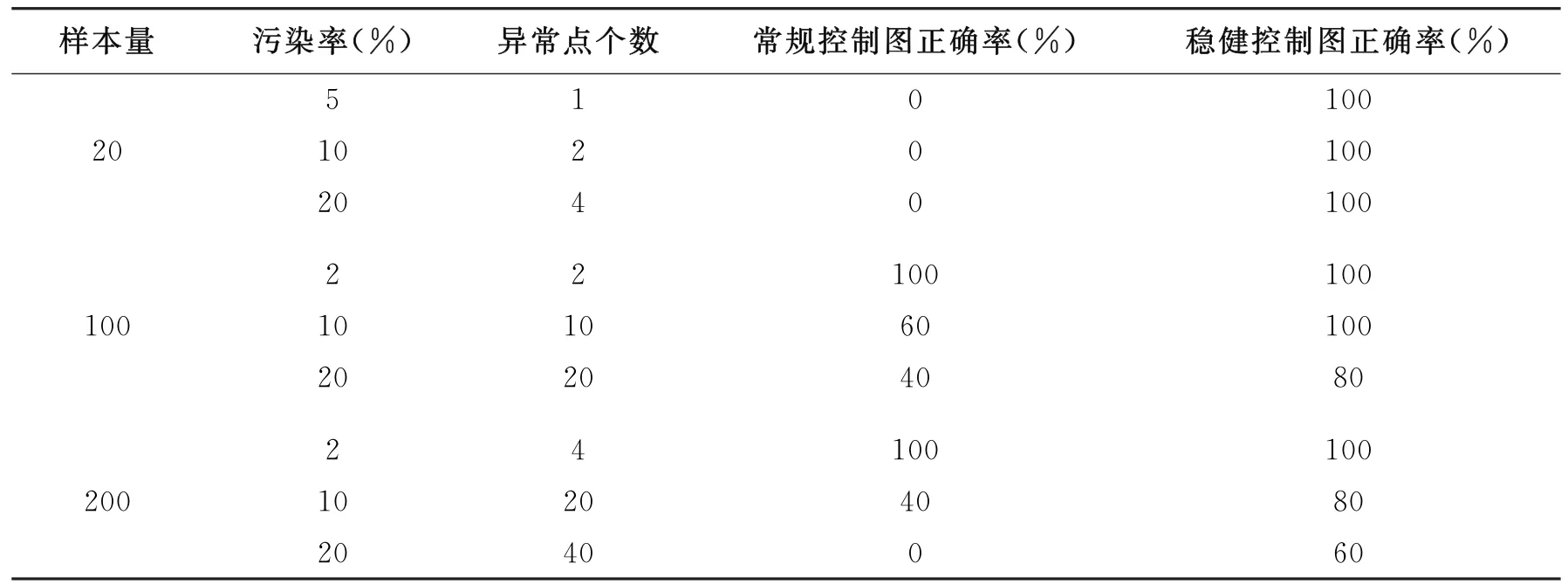
表1 不同样本量不同污染率下的常规与稳健控制图监控效果对比表
从表1可以看出,当样本量为20时,常规控制图在各污染率下的监控正确率全部为0,稳健控制图为100%。当样本量为100与200时,常规控制图与稳健控制图的报警正确率均随着污染率的增加而减少,但稳健控制图报警正确率一直显著高于常规控制图且数值相对稳定。
4 实证检验
为进一步检验本研究所提出的基于HL1-MAD 组合估计量所改进的稳健控制图对含异常值序列的监控效果,本文选取2019年8月22日-2020年6月19日泰山石油(代码:000554.SZ)收益率作为受控对象。数据来源于英为财情网站(https://cn.investing.com),有效样本量为200。泰山石油数据的探索性分析结果如图3所示。
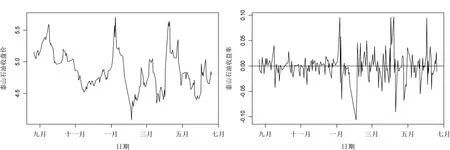
图3 泰山石油股票收盘价图(左)与收益率图(右)
图3显示:第一,泰山石油的收盘价图波动幅度很大;第二,泰山石油的收益率图呈现异方差性且存在多个绝对值较大的数,这一特征与本研究目标相吻合。至于绝对值较大的数是否为异常值,则需要通过统计检验进行识别。
采用王志坚、汪志红和王斌会等提出的时间序列异常值稳健检测法[27-30]对泰山石油样本数据进行异常值检测,结果为表2所示。
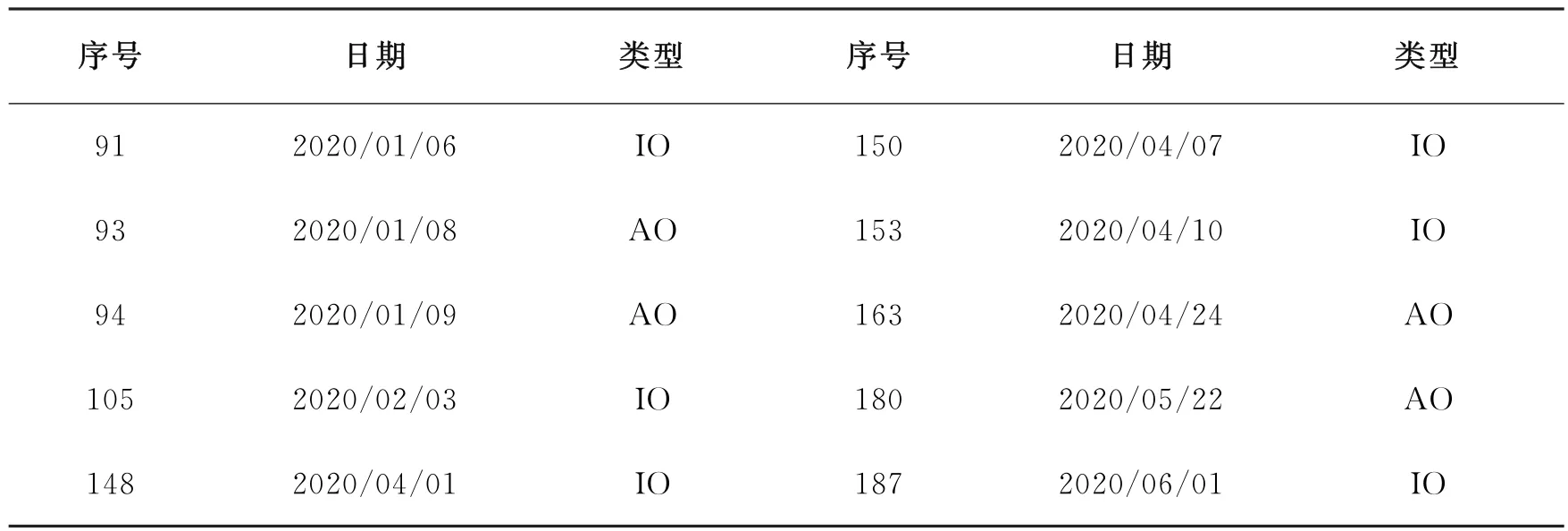
表2 泰山石油收益率异常值检测结果表
从表2可以看出,稳健检测法检测到异常值共10个,其中,6个为IO 型,4个为AO 型。而泰山石油收益率的正态性检验结果显示为:W=0.91653,p value=3.264e-09,即拒绝服从正态分布的原假设。可见,异常值的存在导致序列违背了受控过程满足正态分布假定。
接下来,采用常规控制图与稳健改进控制图分别对收益率序列进行监控,试图通过监控将序列中异常值“报警”出来,监控结果见图4。
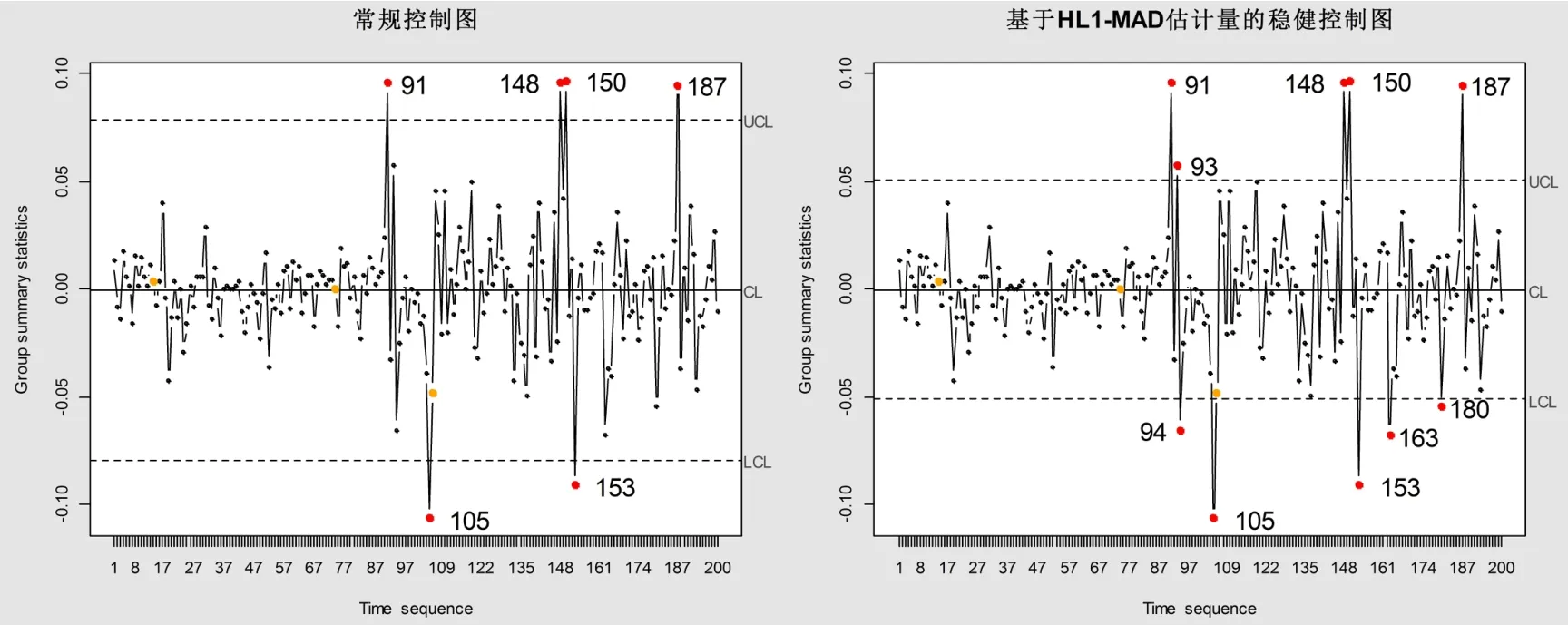
图4 常规控制图(左)与稳健控制图(右)监控结果图
从图4可以看出,常规控制图出现6个异常值报警,序号分别是:91、105、148、150、153、187。稳健控制图出现10个异常值报警,序号分别是:91、93、94、105、148、150、153、163、180、187。常规控制图漏报警4个异常值,报警正确率60%,稳健控制图所报警异常值个数与稳健检测法检测到异常点个数一致,报警正确率100%。泰山石油收益率的实证结果进一步验证了稳健控制图的可行性与有效性。
5 相对效比较
一个估计量的有效性,通常用相对效率来进行评价,相对效率的概念在各种估计量进行评估比较时非常有用。关于的相对效定义为:
(4)式中分子为估计量的最小方差,分母为实际方差,通常当该比值为1或者接近1时,才认为该估计量是有效的,或者称为相对最优。
泰山石油样本量为200,据此算出泰山石油收益率常用的位置参数与尺度参数估计量的相对效,结果如表3所示。

表3 各估计量的相对效比较
从表3可以看出,位置估计量相对效最小的是中位数median,尺度估计量相对效最小的是极差range。显然中位数是位置估计量的一个很好的稳健估计,而极差并不是尺度估计量的一个好的估计量,但表3显示,极差相对效最小。本文通过对比研究发现,由于控制图的构建涉及到样本均值与标准差两个统计量,仅仅考虑单个统计量的相对效难以构建一个监控效果满意的控制图。因此,需要将位置与尺度统计量两者结合起来构建组合估计量才能得到一个相对最优的稳健控制图。因此,在控制图的稳健估计量的选择问题上,研究者不能仅仅用单个估计量的相对效比较来作为稳健估计量的唯一选取标准,从某种意义上讲,此发现亦是本研究的学术贡献之一。
6 结束语
本研究通过比较并选取均值的稳健估计量HL1与标准差的稳健估计量MAD 作为稳健组合估计量构建了稳健常规控制图,模拟与实证分析均表明本研究构建的稳健控制图能有效地对异常值进行监控。另外,本研究发现,在稳健控制图构建过程中,均值与标准差的稳健估计量不应该分开选取,而要作为一个整体来考虑才能达到更好的效果,这一点在相对效的比较研究中得到了进一步论证。
