Cooperative maneuver decision making for multi-UAV air combat based on incomplete information dynamic game

Zhi Ren ,Dong Zhang ,*,Shuo Tang ,Wei Xiong ,Shu-heng Yang

a School of Astronautics,Northwestern Polytechnical University,Xi'an,710072,China

b Shaanxi Aerospace Flight Vehicle Design Key Laboratory,Northwestern Polytechnical University,Xi'an,710072,China

Keywords:Cooperative maneuver decision Air combat Incomplete information dynamic game Perfect bayes-nash equilibrium Reinforcement learning

ABSTRACT Cooperative autonomous air combat of multiple unmanned aerial vehicles (UAVs) is one of the main combat modes in future air warfare,which becomes even more complicated with highly changeable situation and uncertain information of the opponents.As such,this paper presents a cooperative decision-making method based on incomplete information dynamic game to generate maneuver strategies for multiple UAVs in air combat.Firstly,a cooperative situation assessment model is presented to measure the overall combat situation.Secondly,an incomplete information dynamic game model is proposed to model the dynamic process of air combat,and a dynamic Bayesian network is designed to infer the tactical intention of the opponent.Then a reinforcement learning framework based on multiagent deep deterministic policy gradient is established to obtain the perfect Bayes-Nash equilibrium solution of the air combat game model.Finally,a series of simulations are conducted to verify the effectiveness of the proposed method,and the simulation results show effective synergies and cooperative tactics.

1.Introduction

Unmanned aerial vehicle (UAV) plays an important role in air combat to achieve complex missions through coordinated tactics and maneuvers[1,2].Thus,cooperative maneuver decision making is the key technology of multi-UAV air combat,where cooperative maneuvers are taken to get the better of the opponent and thus accomplish certain missions.Since the maneuver performance and strategies of the opponent is uncertain,the maneuver decision space of UAV becomes more complex as the combat situation varies[3,4].Therefore,how to infer the opponent's strategy and determine the optimal cooperative maneuvering decision according to the current combat situation is the key point of research on cooperative maneuver decision making[5,6].

At present,typical methods that commonly used for air combat decision making include expert system,optimization theory,reinforcement learning,and game theory.The expert system is the earliest decision-making method applied to air combat,which conforms to the analysis and judgments of experienced pilots and models the process of decision making in air combat [7].On the basis of expert system,the air combat model is refined by decomposing the process of decision making into sequential links,including situation awareness assessment [8-10],maneuver intention prediction [11-13],and combat tactic decision [14-17].Considering the requirements and constraints of specific air combat scenarios,optimization theory is introduced to determine the optimal maneuver of certain countermeasures [18,19].With the development of artificial intelligence technology,reinforcement learning has also been applied to air combat decision making.Different from the results of traditional methods,neural network training can emerge new combat tactics and maneuver strategies[20-24].The above studies mainly focused on one-on-one air combat scenario with few variables and small dimensions,while cooperative maneuver of multi-UAV combat is more complex and requires further consideration of highly dynamic combat process and uncertain maneuver strategies of the rivals.Thus,the traditional methods are difficult to be directly applied.

Game theory is a key method to study multilateral decision making,which is applicable for strategy optimization of multiple agents or groups in certain adversarial scenarios with constraints.Li et al.[25] proposed a constraint strategy game approach for cooperative decision making with strict constraints of multi-UAV in air combat.Ha et al.[26]developed a stochastic game model with a sequence of normal-form games for various beyond-visual-range air combat scenarios.Cao et al.[27] proposed a cooperative maneuver decision-making algorithm for weakly connected adversarial environment by combining game models with intuitionistic fuzzy sets.The above studies establish the game model according to specific scenarios,while the opponent's maneuver strategies are considered as complete information,which are not known in the actual air combat.Therefore,it is essential to establish an incomplete information dynamic game model for cooperative maneuver decision making.

Perfect Bayes-Nash equilibrium(PBE)is the Nash Equilibrium of the incomplete information dynamic game,which is usually solved by linear programming [28],counterfactual regret minimization(CFR) algorithm [29],and other deigned methods.However,the incomplete information dynamic game model for multi-UAV air combat has more game phases and larger computational complexity,which makes it difficult to apply the traditional method directly to determine the PBE.Since the neural network has strong fitting ability,it is commonly used in reinforcement learning method to solve the PBE [30,31].In this paper,a PBE solving strategy based on the multi-agent deep deterministic policy gradient(MADDPG)method is proposed,where the actions,states,and rewards are designed based on the corresponding elements of multi-UAV combat scenario and the game model.

The main contributions of this paper are given as follows:

(i) A cooperative maneuver decision-making method based on incomplete information dynamic game model is proposed,considering the high dynamics and uncertainties of the opponents in air combat.

(ii) A reinforcement learning framework based on MADDPG is established to determine the perfect Bayes-Nash equilibrium of the proposed air combat game model.

The remainder of this paper is organized as follows.Section 2 introduces the UAV maneuver model and the cooperative air combat situation assessment model.In Section 3,the incomplete information dynamic game model for cooperative maneuver decision making in multi-UAV air combat is proposed,and the dynamic Bayesian network is applied to infer the incomplete information.Section 4 discusses the existence of PBE and establishes the MADDPG framework.The simulation experiments are conducted and analyzed in Section 5,and Section 6 concludes this paper.

2.Problem formulation

Cooperative maneuver decision making requires to consider the real-time situation and the opponent's maneuver strategies,where the determined tactical maneuvers are carried out to achieve the advantage of the overall air combat situation,and thus win the combat.

2.1.UAV maneuver model

The flight trajectory of UAV can be decomposed into seven elemental maneuvers,including max load factor turns,max long acceleration,steady flight,max long deceleration,max load factor pull up and max load factor push over[32].The combination of the elemental maneuvers allows for complex tactical maneuverers such as kindle,split-S,yoyo,etc.In this paper,the elemental maneuvers in five directions are expanded by considering the speed variation.The control strategy of maneuvering in any directions and variation can be described by tangential overload,normal overload and bank angle to generate,which is shown in Fig.1.

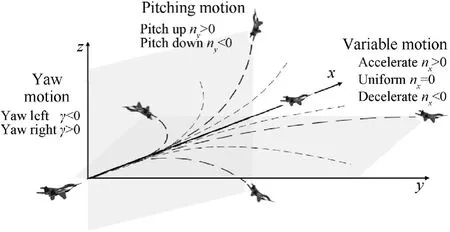
Fig.1.Control strategy of maneuvering in any directions and variation.

The kinematics and dynamics model of UAV in inertial coordinate system is as follows:

whereVis the velocity of UAV,x,yare the horizonal coordinates,zis the altitude,θ is the flight path angle,φ is the heading angle,γ is the bank angle,nxis the tangential overload,nyis the normal overload andgis acceleration of gravity.Besides,the tangential overload enables acceleration,deceleration and uniformity flight;the normal overload enables pitching motion;and the bank angle enables yaw motion.Therefore,with certain control strategies,the maneuvers in all directions and variation can be generated under the constraints of control variables and flight performance,which are considered as follows:

wherenxminis the minimum available tangential overload,nxmaxis the maximum available tangential overload,nyminis the minimum available normal overload,nymaxis the maximum available normal overload,Vminis the minimum velocity,andVmaxis the maximum velocity that UAV can reach.In particular,the control boundary of overload and velocity represents the maneuverability of UAV.

2.2.Cooperative situation assessment model

Situation assessment is the premise of maneuver decision making,where the survival threat and combat edge are measured to provide decision basis for maneuver decision making.In one-onone air combat situation assessment,the air combat situation includes advantage,balance and disadvantage,according to the relative position and velocity direction of two combatants.The spatial geometric relationship of UAV is shown in Fig.2.

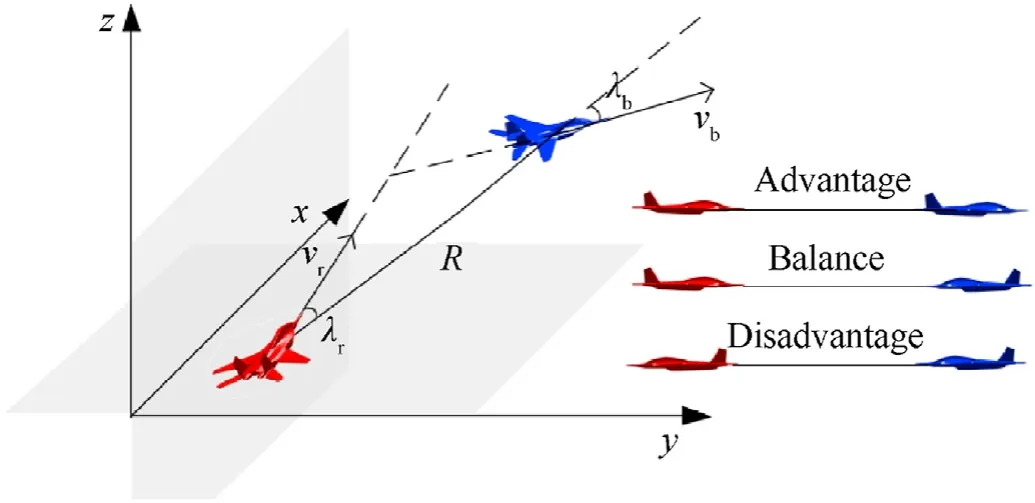
Fig.2.Air combat geometry situation.

Fig.2 shows the relative course angle λibetween the combatants,which can be calculated by

whereR=[xr-xb,yr-yb,zr-zb]Tis position vector,vi=[cos θisin φi,cos θisin φi,sin θi]Tis velocity vector,r and b represents for the UAVs of the red side and the blue side,respectively.

The relative situation of UAV air combat is quantitatively described by the situation function based on the relative position and posture.Considering the angle advantageuθ,uφand distance advantageudas the main component of the situation function[33],which can be calculated by

where ωθ,ωφ,ωdis the weight coefficient of angle advantage and distance advantage,respectively.

It is easy to see that the larger the situation function is,the more likely the UAV is to survive and destroy the opponent.On this basis,the situation function matrix is designed as follows:

whereUis the situation function matrix of m-on-n air combat anduijis the one-on-one combat situation between UAVi=1,2,…,mand UAVj=1,2,…,n.On this basis,the overall situation is determined by considering the cooperative combat tactics.Assume that each UAV can only choose one rival as the target in the process of muti-UAV air combat,then the opponenteiwith the largest value of situation function will be selected as the target,which is described as follows:

Suppose that the UAVs with the same target can form cooperative combat tactics through certain maneuvers,and the overall cooperative situation will be improved with such cooperative effect.Assume that the combat situation among the UAVs with the same target is independent of each other,then the overall cooperative situationof UAViis defined as follows:

3.Multi-UAV air combat game model

3.1.Incomplete information dynamic game

The incomplete information of the game model refers to a lack of full information by the players about the normal form of the game,such as some other players' strategy spaces and utility functions[34].In air combat problems,the tactical intention refers to the UAV's adoption of pursuit or evasion strategy according to the real-time situation,which determines the combat strategies and corresponding maneuvers.Since the opponents' preference of tactical intention is uncertain,the incomplete information of the players in the game model corresponds to the preference of the tactical intention.On this basis,a virtual player “nature”is introduced through Harsanyi transformation [35] to set the type of player,which transforms a dynamic game of incomplete information into a dynamic game of complete but imperfect information.Fig.3 shows the extensive form of the incomplete information dynamic game model for multi-UAV air combat.

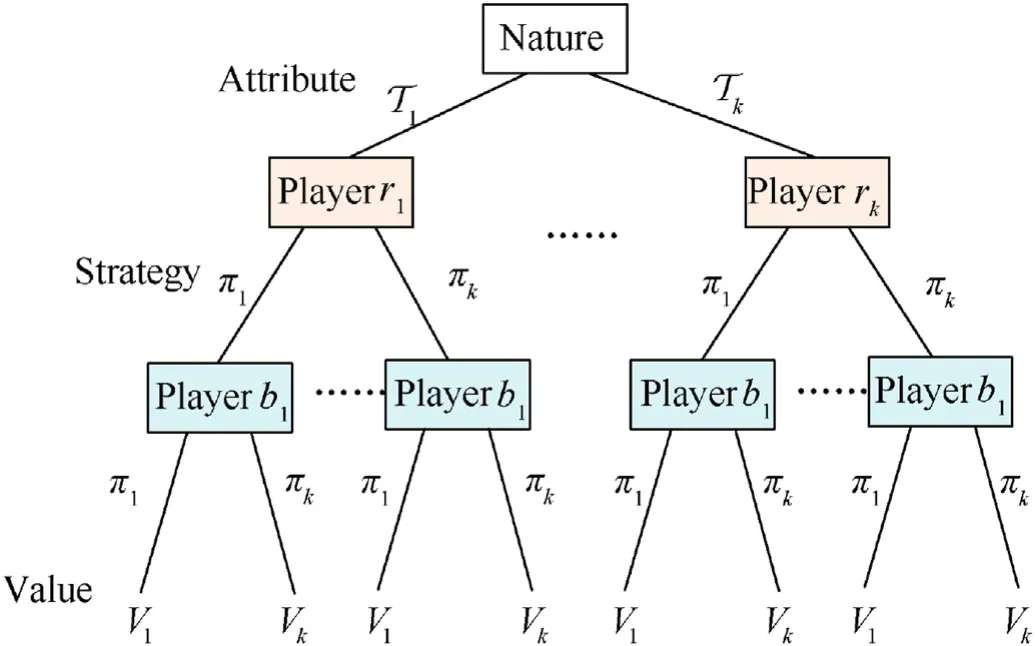
Fig.3.Extensive form game.

On this basis,we formulate the incomplete information dynamic gameG=[N,T,Π,V] as follows:

•N={r1,r2,…,rm,b1,b2,…,bn}denotes the player set of multi-UAV air combat game,rrepresents for the UAVs of the red side,andbrepresents for the UAVs of the blue side.

•T={T1,T2,…,Tl} is type set of the player andpTis the corresponding probability density,where Tiis the type of playeriand represents for the tactical intention of UAV.Suppose that Tiis independent of each other and obey the normal distribution.The larger Tiis,the more likely that UAV prefers to adopt pursuit and attack strategy rather than evasion and defense strategy.

• Π={π1,π2,…,πk} is the strategy set andpπis the probability density of the mixed strategies,which represents that playeritakes the actionof the corresponding maneuver based on the determined tactical attention Ti,and the state transfers into

•Vdenotes the utility function of the game and represents the pay-off of certain mixed strategies.

Suppose that the main goal of the cooperative maneuver decision making is to maintain or improve the overall air combat situation with consideration of the synergies and coordination.Therefore,the overall cooperative situation of the players after the maneuver state transfer is used as the utility function of the corresponding mixed strategies,which is defined as follows:

3.2.Dynamic Bayesian network inference

In the incomplete information dynamic game of multi-UAV air combat,the type of the red side is set by“nature”,while the type of the blue side is inferred through dynamic Bayesian network based on the prior knowledge,including the state transition probability and the prior probability distribution.A Bayesian network consists of nodes and directed edges,where each node represents a random variable and each directed edge represents the causal relationship between two variables,which can be denoted as follows:

whereX={x0,x1,…,xn-1} is the joint probability distribution of state variables,Y={y0,y1,…,yn-1} is the joint probability distribution of observed variables,P(xt|xt-1) is the probability distribution of the state transfer between the neighboring state variables,P(yt|xt)is the probability distribution of state transfer between the observed variable and the neighboring state variable,andP(x0) is the probability of the initial state variable.

Since the type of the player determines the tactical intention preference and the corresponding maneuvers of UAV in the realtime combat situation,the change pattern of the state parameters indicates the characteristic of certain maneuvers.Moreover,the state parameters of the opponent,such as the position and velocity,can be observed by the airborne radar during the process of the air combat.Therefore,the dynamic Bayesian network is divided into a decision layer and a feature layer.Fig.4 shows the structure of the designed dynamic Bayesian network,where the feature layer selects velocity,heading angle and altitude as the observed variables,and the decision layer selects type of the blue side,tactical intention decision and maneuver decision as the state variables.

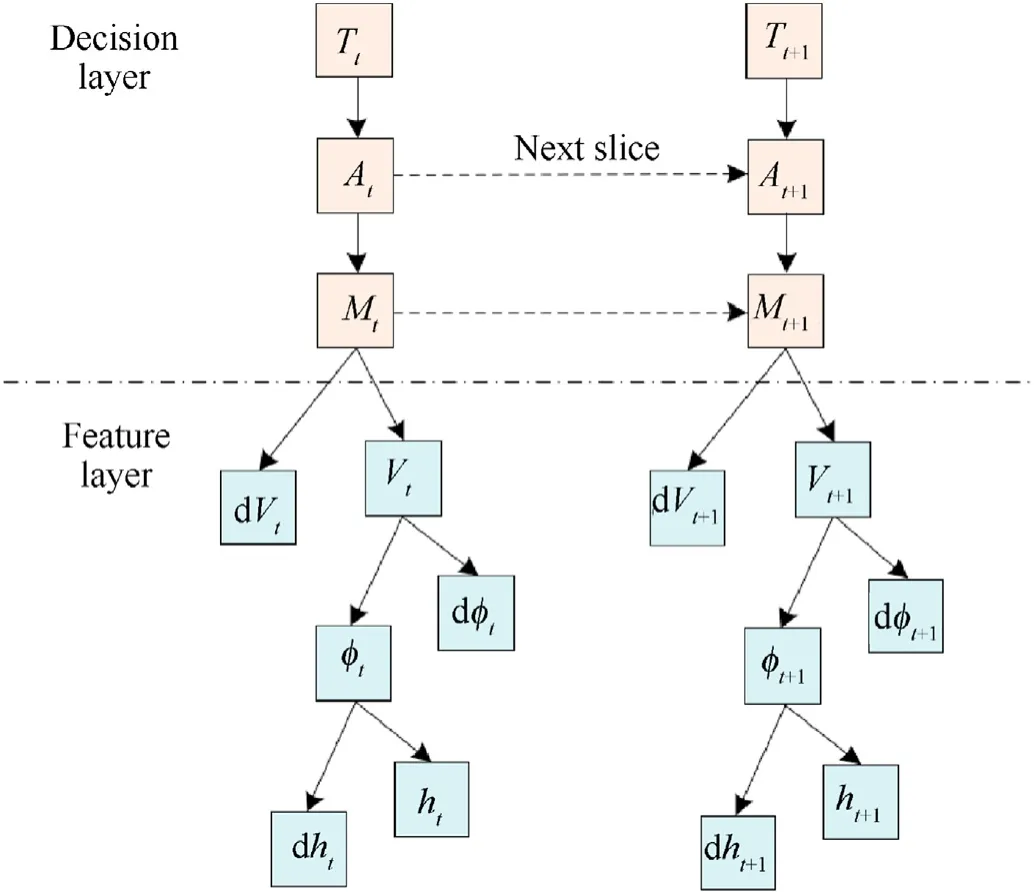
Fig.4.Structure of dynamic Bayesian network.

According to the Bayesian theorem and the designed dynamic

Bayesian network,the conditional probability of the tactical intention that the blue side takes in condition of the corresponding statesis calculated by wheregbis the specific tactical intention of the blue side,e1:tdenotes the sequence information of the state variables of maneuvers and the neighboring observed variable before timet,Atrepresents the state variable of tactical intention.

In the stage of multi-UAV air combat game,the players of the red side iteratively estimate the type and maneuver of the blue side based on the probability distribution set by“nature”.Let Trbe the type of the red side set by “nature”,andsbis the priori state information of the blue side,then the inferred type of the blue side Tbis calculated by

4.PBE solution strategy

4.1.PBE existence analysis

Perfect Bayes-Nash equilibrium is the strategy evaluation of the incomplete information dynamic game model as a combination of inferred probabilities and mixed strategies [36].In muti-UAV air combat,when state and posture of the blue side is given,the red side can infer the type and tactical intention based on the real-time combat situation,and the corresponding PBE can ensure that the overall combat situation in the subsequent game at any decision stage is optimal compared to other strategies.The PBE of the proposed multi-UAV air combat game model is defined as follows:

Combining Eq.(6) and Eq.(7),it is easy to see that the utility function is continuous with upper and lower bounds on the function values between (0,1).Meanwhile,the utility function is discrete as the game stages disperse.Therefore,for each maneuver strategy in any stage of the air combat game,the other maneuvers will either improve or worsen the situation,which satisfies the following:

Thus,the proposed gameG=[N,T,pT,Π,pπ,V] satisfies strong uniform payoff security[36]and that for each T ∊T,the maneuver strategy Π described by tangential overload,normal overload and bank angle has upper semicontinuous.Then,according to the PBE existence theorem proposed by Carbonell et al.[37],the proposed air combat game must possess a perfect Bayes-Nash equilibrium,which shows that the proposed maneuver decision method can achieve the tactical intention and guarantee the advantage of the overall air combat situation.

4.2.MADDPG training framework

The basic process of the reinforcement learning method is iteratively transferring actions and states through policy optimization to acquire the maximum sum of rewards.MADDPG is based on the Actor-Critic method,in which multiple neural networks are connected in parallel with centralized learning and distributed execution.During the training process,the actor network uses an off-line policy to generate the training dataset and playback the empirical data.The critic network samples the training dataset based on the strategy net-work and then iteratively learns the optimal strategy.The specific structure of MADDPG designed for determining PBE of the proposed game model is shown in Fig.5.

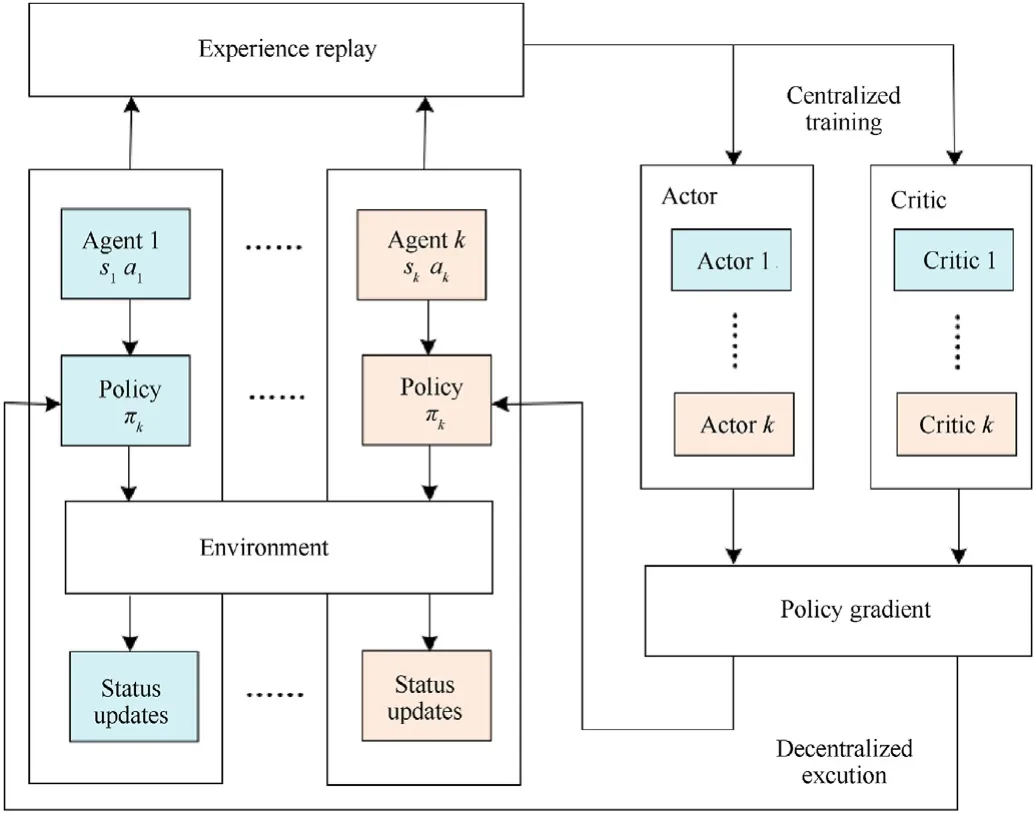
Fig.5.Structure of MADDPG network.

The MADDPG training model is established based on the proposed game model to solve the Perfect Bayes-Nash equilibrium.In the MADDPG model,the agents correspond to the players in the game model,which represents for the UAV in the air combat.The state is set as the position of UAV in the air combat,and the action is set as the maneuver control of UAV,which corresponds to the action of the pure strategy in the proposed game model.Thus,the training result of the policy corresponds to the Perfect Bayes-Nash equilibrium of mixed strategy.

The reward of the reinforcement model determines the expectation of the policy convergence of the strategy learning iterations,and the agent is trained to maximize the final cumulative reward through iterative learning.As noted in Eq.(11),the mixed strategy of Perfect Bayes-Nash equilibrium denotes the largest utility.Therefore,the utility function in the dynamic game model can be used as the reward function of the reinforcement learning model,which is designed as follows:

Suppose that the MADDPG trainsmagents of the red side against the blue side,the policy of each agent is denoted asTo estimate the parameters of the actor and critic network σ∊{θμ,θQ},respectively,the gradient descent method is introduced and calculated by the follows:

In summary,the decision-making process of multi-UAV cooperative maneuver based on incomplete information dynamic game is illustrated in Fig.6.During the combat,each step of maneuver decision-making is considered as a stage of dynamic game.Firstly,the proposed dynamic games of incomplete information transfer to dynamic games of complete information by Harsanyi transformation,where the“nature”selects the type of both players and the Bayesian network infers the tactical intention of the opponents.Then the perfect Bayes-Nash equilibrium is solved,and the cooperative maneuver is decided to gain the advantage of overall situation.In particular,the perfect Bayes-Nash equilibrium is a mixed strategy of certain maneuvers with corresponding probabilities,where the state of UAV after maneuver decision is determined in each step as follows:

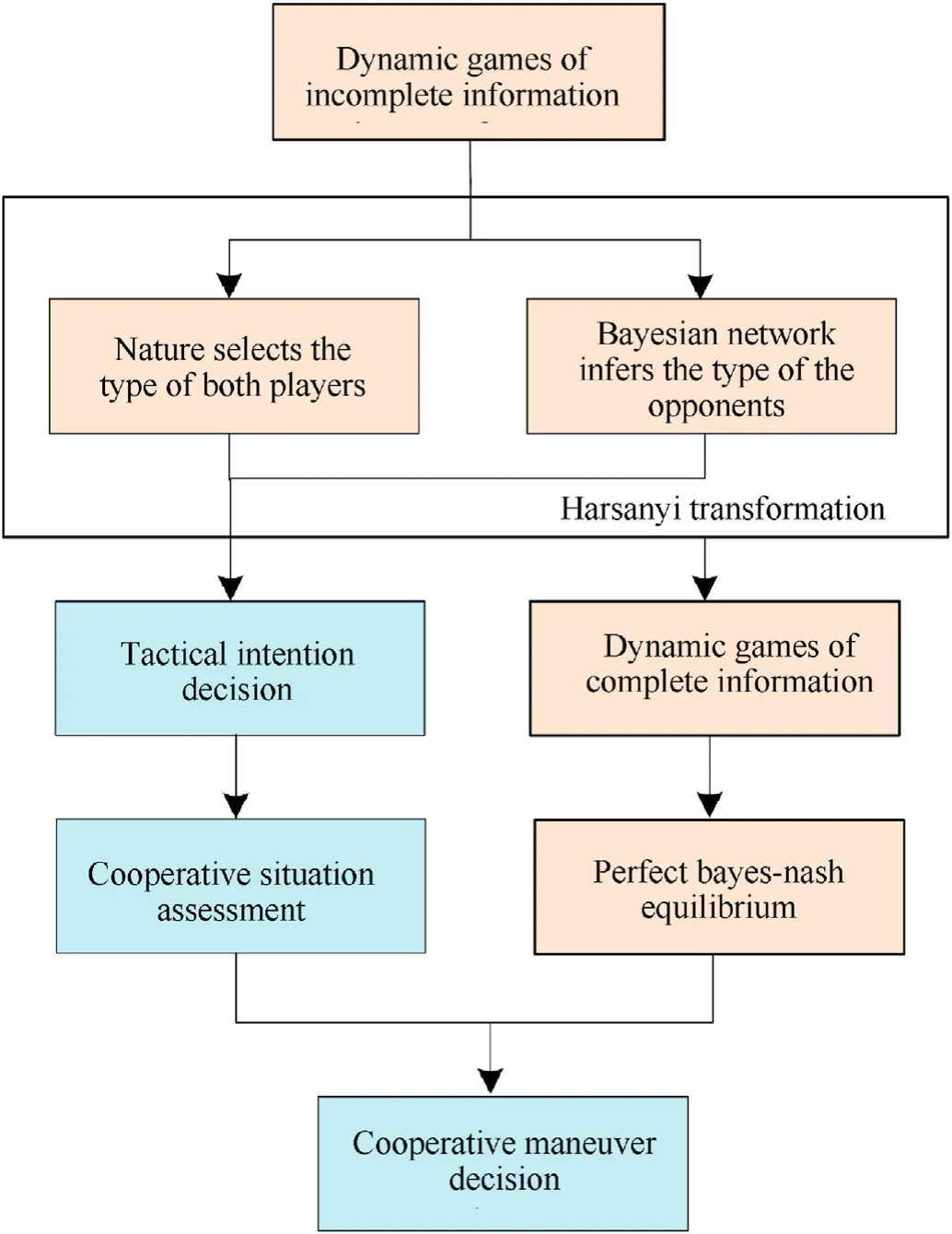
Fig.6.Cooperative maneuver decision making process.

5.Experimental results and analysis

5.1.Platform setting

In the process of air combat,suppose that the effective attack range of the UAV is a sector related to the firing angle and attack distance of the airborne weapon.When the opponent is within the attack range for a sustained period of time,it is considered as a success of air combat.Also,suppose that the effective detection range of the UAV is a sector related to the directional angle of the airborne radar and the detection range of the opponent.When the opponent is outside the detection range for a sustained period of time,it is considered that the UAV has evaded from the opponent.The typical air combat process of pursuit and evasion is shown in Fig.7.

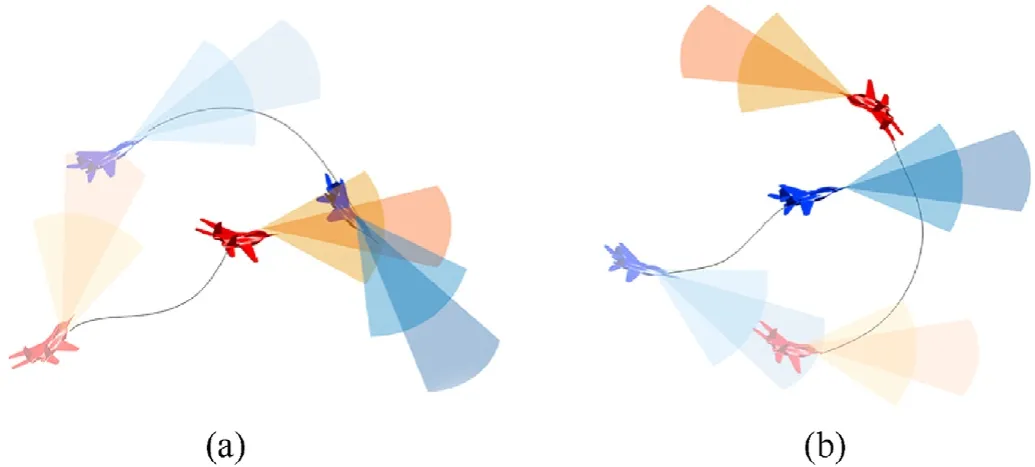
Fig.7.Typical air combat process: (a) Pursuit;(b) Evasion.

The simulation experiments are designed in several sets of different postures of air combat scenario based on Zhang et al.[38].Firstly,a two-on-two air combat scenario is designed to verify the effectiveness of the proposed method.On this basis,further simulations are conducted for two-on-three and three-on-two air combat scenarios.In the simulations,the red side adopts the proposed cooperative maneuver decision method,and the blue side adopts the maneuver strategy that proposed by Ma et al.[39].Assume that UAVs of both sides have the same performance,and the parameter settings are designed based on Zhang et al.[38],where the initial flight speed of UAV is 200 m/s,the maximum detection distance is 6000 m,the maximum directional angle is 45°,the maximum attack distance is 1000 m,and the maximum attack angle is 60°,the minimum available tangential overload is -1,the maximum available tangential overload is 2,the minimum available normal overload is 0,the maximum available normal overload is 8,the minimum flight velocity is 90 m/s,and the maximum flight velocity is 400 m/s.The air combat will come to an end when either side completes its tactical intention.

The equipment configuration is Intel(R) Core (TM) i9-10885H CPU,NIVIDA GeForce RTX 2070 Super,and the TensorFlow-GPU 2.1.0 environment is built by CUDA10.1 to construct the MADDPG training framework for the proposed game mode.The neural network parameters are shown in Table 1.

Table 1 Convolutional neural network parameters.

5.2.Simulation results and analysis

5.2.1.Algorithm performance comparison and analysis

A two-on-two combat scenario(scenario 1)is designed to verify the Perfect Bayes-Nash equilibrium solution strategy and the combat effectiveness of the proposed model.The specific initial conditions are shown in Table 2,where the red side is within the detection range ahead of the blue side,and the overall air combat situation is at a disadvantage.

Table 2 Initial state of two-on-two air combat.

(A) PBE solution strategy simulation The Perfect Bayes-Nash equilibrium of two-on-two combat scenario is firstly trained by the proposed MADDPG method,and the TD3 method[40]is lately applied as comparative test to verify the PBE solution strategy.The cumulative reward of the proposed MADDPG method and TD3 method is shown in Fig.8,and the exploitability of both is shown in Fig.9(a) and Fig.9(b),respectively.

Fig.8.Cumulative reward of PBE solution strategy: (a) MADDG;(b) TD3.

Fig.9.Exploitability of PBE solution strategy: (a) MADDG;(b) TD3.

The cumulative reward and exploitability of the training results show that the proposed solution strategy can converge to estimate the Perfect Bayes-Nash equilibrium with fewer iterations and oscillations than TD3.It is because that the MADDPG method has good performance in large-scale space and depth with centralized training of multiple actor and critic networks rather than relaying the update of the actor network,and thus achieve better results with higher efficiency.

(B) Deviation simulation case

During the process of air combat,the observation of the opponents’ states has a great impact on maneuver decision making.To further verify the combat effectiveness of the proposed incomplete information dynamic game model,the noise is used to deviate the input observation of the opponent’s state parameters.

Fig.10 shows the combat trajectory of two-on-two air combat with accurate observation.In the initial stage of the combat,the two UAVs of the red side separate and use outflanking tactics,where the left-wing UAV takes an S-shaped maneuver to evade and the right-wing UAV staggers to the left to accelerate in a dive;the blue side also adopts a separation strategy to track and pursue.In the later stages of the combat,the left-wing UAV of the red side makes a large overload maneuver of kindle to gain the advantage over the blue side and counter back,and the other one accelerates with a yoyo maneuver to take turn in the direction of the teammate,while the blue side maintains constant tracking but loses its original advantage of overall air combat situation.

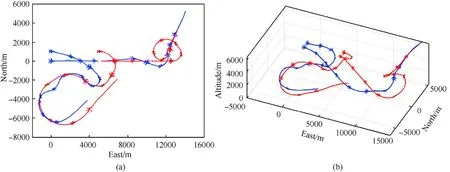
Fig.10.Combat trajectory of two-on-two air combat with accurate observation: (a) Top view of two-on-two-combat;(b) Three-dimensional view of two-on-two combat.

Fig.11 shows the combat trajectory of two-on-two air combat with deviations,where the red side remains outflanking tactic and the blue side keeps constant tracking after separation.Although the UAVs of red side take the maneuvering trajectories different from the accurate case during the process of combat,they realize the outflanking tactic and form the pincer situation on the back of the opponent in the later stages of the combat.The deviation of the expected opponents’state parameters directly affects calculation of the overall situation and misleads the optimal response maneuvering against the opponent.Therefore,the mixed strategies of Perfect Bayes-Nash equilibrium change and the maneuvering trajectories differ from the accurate case.However,the comparative simulation shows that the Perfect Bayes-Nash equilibrium remains coherent tactical strategy,which verifies the combat effectiveness of the proposed model.

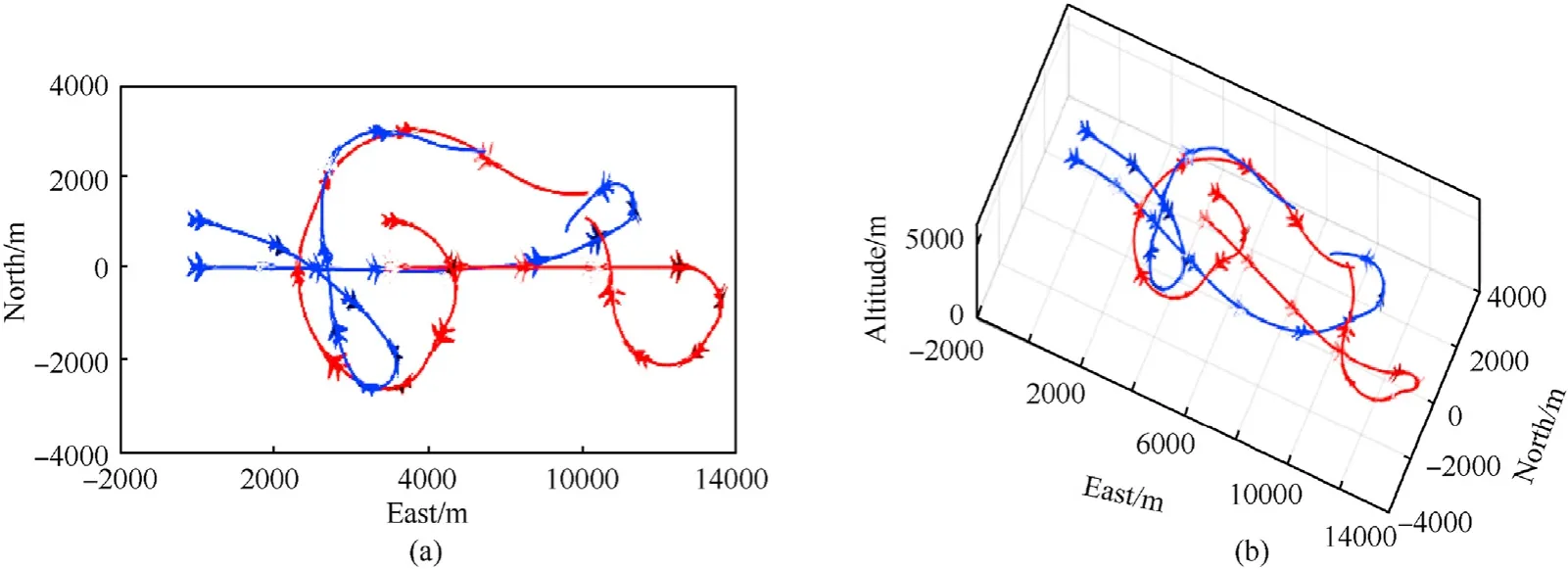
Fig.11.Combat trajectory of two-on-two air combat with deviations: (a) Top view of two-on-two-combat;(b) Three-dimensional view of two-on-two.

5.2.2.Air combat simulation examples

(A) Two-on-three air combat simulation

To further verify the effectiveness of the proposed method,a two-on-three air combat scenario(scenario 2)is designed based on scenario 1,where the red side is within the detection range of the blue side with,and the overall air combat situation is at a disadvantage.The initial conditions are shown in Table 3.The proposed method is solved by MADDPG for 25,000 generations,and the cumulative reward is shown in Fig.12.

Table 3 Initial state of two-on-three air combat.

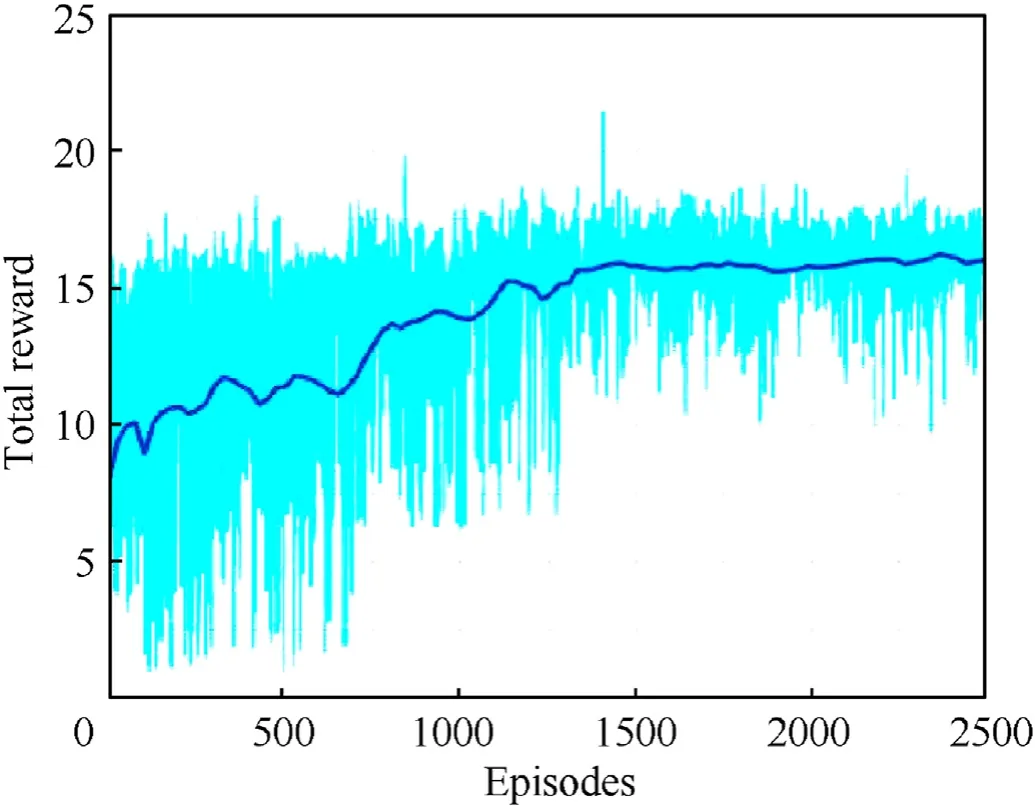
Fig.12.Cumulative reward for two-on-three air combat.

The result of the combat trajectory is shown in Fig.13.During the progress of air combat,the UAVs of the red side adopt decoy tactics,where one UAV makes a large overload maneuver of detour and pull up to evade,and the other UAV slows down as a decoy and attempts to make an S-shaped maneuver to achieve situation advantage.The three UAVs of the blue side are distracted by the decoy UAV of the red side.The right-wing approaches the teammate and pulls up to slow down in accordance with the overall combat situation,while the other UAVs continuously track and pursue the decoy UAV of the red side.In the later stage of the combat,the red side completes the tactical escape and takes the advantage,while the blue side has difficulty in coping with the red side,due to its decision to pursue the decoy UAV of the red side at the early stage of the air combat.At last,two UAVs of the blue side end up with a disadvantage situation of being with the attack range of the red side.

Comparing the simulation results of scenario 1 and scenario 2,it can be seen that the red side determines a tactical intention to escape,but adopts a different maneuver strategy.In scenario 1,the UAVs of the red side separate first but approach at the end of the combat for coordinate support,while in scenario 2 the UAVs of the red side use decoy tactics to leave the battlefield and do not support with the teammate.The above simulation comparison can verify the effectiveness of the proposed method under different scenarios,and the Nash equilibrium combat strategies show synergies of multi-UAV air combat effectively.

(B) Three-on-two air combat simulation

To further study the superiority of the proposed method,the three-on-two air combat scenario(scenario 3)is established based on the scenario 2,where the initial states of the red side and the blue side are swapped to compare the air combat result of switched strategies.The initial conditions are shown in Table 4.The proposed method is solved by MADDPG for 25,000 generations,and the cumulative reward is shown in Fig.14.

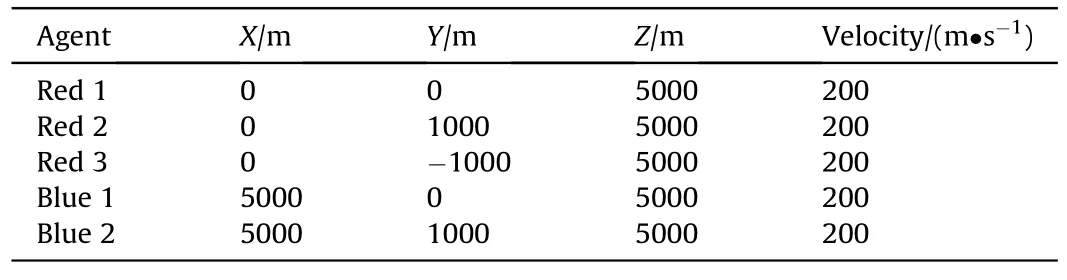
Table 4 Initial state of two-on-three air combat.

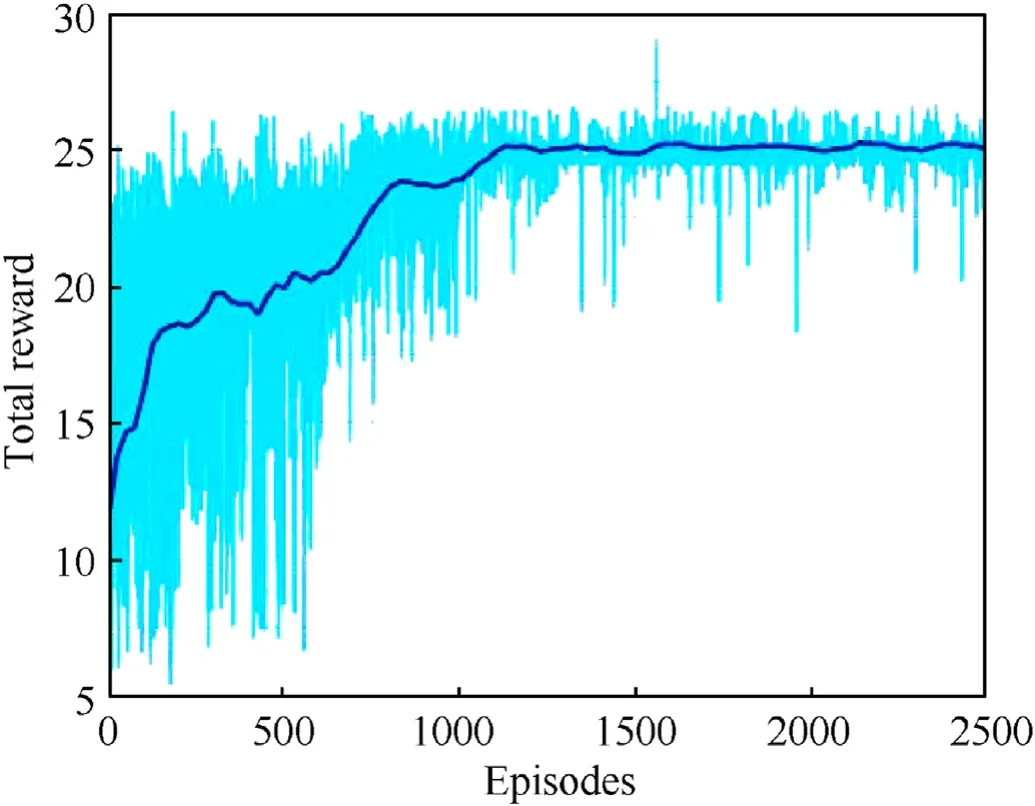
Fig.14.Cumulative reward for three-on-two air combat.

The result of the combat trajectory is shown in Fig.15.In the initial stage of the combat,the blue side is within the detection range ahead of the red side,where the UAVs of the red side takes the overall situation advantage.During the air combat,the two ambilateral UAVs of the red side firstly pull up and take the altitude advantage to track the left-wing UAV of the blue side,and the middle UAV dives to accelerate and keeps tracking the right-wing UAV of the blue side.Then the red side completes the formation change to keep the target pursuit and the overall situation advantage.The UAVs of the blue side adopt a half roll and split-S maneuver to reverse the posture and pine down to accelerate to storm the front.In the end,the red side forms a pincer movement and the blue side loses the combat.

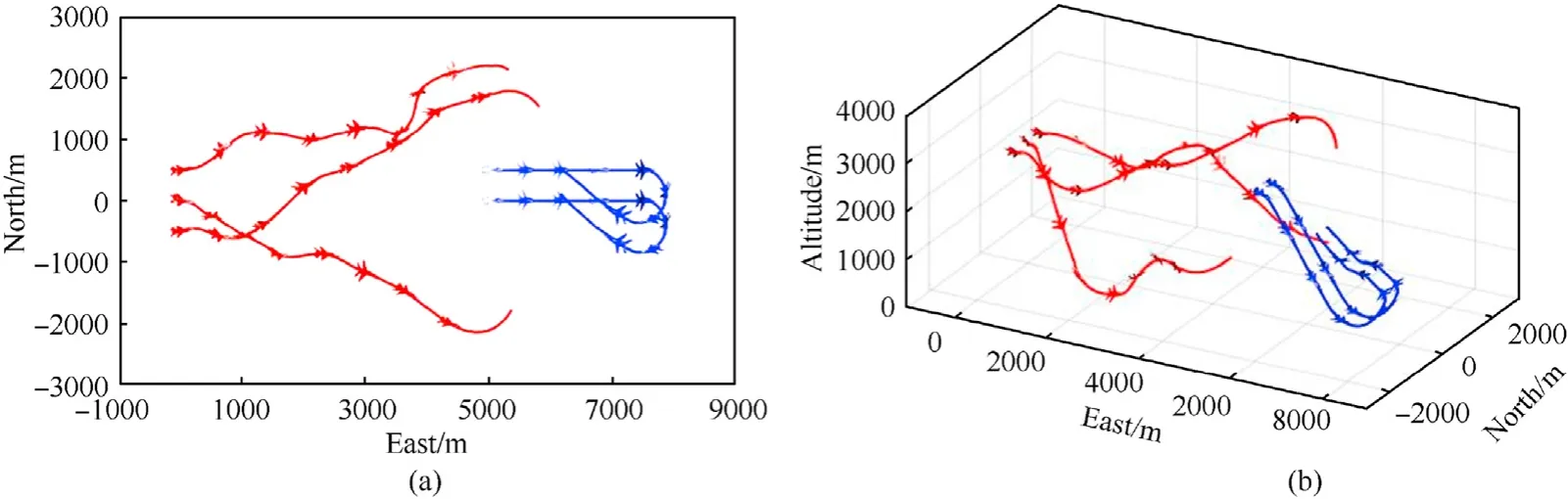
Fig.15.Combat trajectory of three-on-two air combat: (a) Top view of two-on-two-combat;(b) Three-dimensional view of three-on-two combat.

Comparing the simulation results of scenario 2 and scenario 3,it can be seen that the Nash equilibrium strategy of the proposed method shows effective synergies,which rediscovers and verifies existing cooperative tactics in multi-UAV air combat,including decoy tactics and pincer movement shown in Fig.16.

6.Conclusions

In this paper,an incomplete information dynamic game theory approach is used to model the progress of multi-UAV air combat and a dynamic Bayesian network is designed to infer the incomplete information of the opponent’s preference type on tactical intention.The perfect Bayes-Nash equilibrium strategy is solved by reinforcement learning framework based on MADDPG to address the cooperative maneuver decision-making problem.The simulations verify the effectiveness of the proposed method and the results show that the perfect Bayes-Nash equilibrium strategy can generate multiple effective synergies and cooperative tactics in different scenarios.The proposed method has superiority to achieve the advantage of overall combat situation.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No.61933010 and 61903301),and Shaanxi Aerospace Flight Vehicle Design Key Laboratory.