Model-based deep learning for fiber bundle infrared image restoration

Bo-wen Wang ,Le Li ,Hai-bo Yang ,Jia-xin Chen ,Yu-hai Li ,Qian Chen ,Chao Zuo ,*

a Jiangsu Key Laboratory of Spectral Imaging and Intelligent Sense,Nanjing University of Science and Technology,Nanjing,Jiangsu Province,210094,China

b Smart Computational Imaging (SCI) Laboratory,Nanjing University of Science and Technology,Nanjing,Jiangsu Province,210094,China

c Science and Technology on Electro-Optical Information Security Control Lab,Tianjin,300308,China

Keywords:Fiber bundle Deep learning Infrared imaging Image restoration

ABSTRACT As the representative of flexibility in optical imaging media,in recent years,fiber bundles have emerged as a promising architecture in the development of compact visual systems.Dedicated to tackling the problems of universal honeycomb artifacts and low signal-to-noise ratio(SNR) imaging in fiber bundles,the iterative super-resolution reconstruction network based on a physical model is proposed.Under the constraint of solving the two subproblems of data fidelity and prior regularization term alternately,the network can efficiently “regenerate”the lost spatial resolution with deep learning.By building and calibrating a dual-path imaging system,the real-world dataset where paired low-resolution(LR) -highresolution (HR) images on the same scene can be generated simultaneously.Numerical results on both the United States Air Force (USAF) resolution target and complex target objects demonstrate that the algorithm can restore high-contrast images without pixilated noise.On the basis of super-resolution reconstruction,compound eye image composition based on fiber bundle is also embedded in this paper for the actual imaging requirements.The proposed work is the first to apply a physical model-based deep learning network to fiber bundle imaging in the infrared band,effectively promoting the engineering application of thermal radiation detection.

1.Introduction

The fiber bundle imaging technique has demonstrated its success in military periscope,life detection,and endoscopic imaging[1],owing to the inherent flexibility of fiber optics.In the military field,the fiber bundle periscope combines the flexible passive fiber optic image transmission system with the internal sighting scope,enabling the shooter to conveniently utilize corners,tree trunks,trenches,high platforms,and other terrain features for periscopic hidden observation and rapid aiming and firing on targets.By constructing a compact set of lenses,multiple LR sub-images are formed in the compound eye system[2,3],and composited sub-eye images are achieved by post-processing.In addition,combining the advantages of infrared imaging [4] and fiber-optic sensing can provide more valuable technical approaches to the field of detection and open up a variety of applications.Meanwhile,in turn,limited by its geometric nature (irregular layouts of fiber cores),images taken by such systems have penetrated honeycomb-like fixed pattern noises [5,6].Infrared images are accompanied by a significant non-uniformity effort,which damages the imaging performance rather than helping it [7,8].In addition,the effective imaging resolution of a fiber bundle system is capped by the inherent physical fiber core diameter and fiber density rather than the optical system or the detector pixel size.Image restoration possibility is also considered the potential of the compound-eye system,which is yet to be explored fully.Therefore,there is an urgent requirement for an effective algorithm to improve the spatial imaging resolution while separating the honeycomb patterns,which is the motivation of this paper.

Most current imaging applications of fiber bundles are applied in micro-endoscopic,which are typically accompanied by poor light transmission(incoming light intensity information)due to the minor incident numerical aperture of the fiber bundle.Therefore,the low SNR in far-field imaging is also a huge challenge,which progressively hinders the accurate analysis of objects.In order to optimize the imaging perception of the optical fiber bundle technique,it is necessary to explore implementable methods to eliminate the impact of honeycomb patterns and compensate for the mixed texture information.Corresponding optimization methods have been presented successively.Earlier computational methods were generally implemented a prior by the regularity of fiber pattern arrangement.Rupp[9]borrowed the interpolation method in the spatial domain to establish the exact position relationship of each fiber center pixel point and subsequently interpolates the cladding pixels based on the values of the neighboring pixel points.Shinde [10] proposed that the honeycomb structure image is regularly arranged in the frequency domain,and the envisioned data can be recovered using the band-stop filtering technique,yet it is hugely challenging to determine the threshold of the band-stop filter,which normally results in part of the valuable information being filtered as well.However,previous computational methods only eliminated undesired pixelated patterns without substantial improvement in spatial resolution.

Super-resolution is an ill-posed problem[11-14]that deals with restoring an HR image from a single or a series of raw images based on either specific a prior knowledge or just an assumed generic notion about the tighter correspondence imaging model.The deep learning technique [15-17] breaks the dependence of traditional methods on prior knowledge and efficiently utilizes the raw information “hidden”in the original honeycomb patterns.Minimizing the optimization problem by mapping massive data samples [18,19] (deep learning methods gradually reduce the loss function through multiple epochs and update the weight parameters through feedback),is conducive to precisely learning the highresolution image.In particular,U-Net [20] has achieved tremendous success in searching the mapping functions (observation models and noise statistics) for various underdetermined medical imaging problems,verifying the feasibility of constraining the inverse problem through the network.Ravi [21] estimated the pseudo ground truth image by a video alignment algorithm and then tried to recover the fiber bundle image by three different convolutional neural networks.Simultaneously,Shao [22] implemented a generative adversarial restoration neural network(GARNN) or a 3D convolution network to remove the foveal effect and restore the “hidden”features.The feasibility of superresolution reconstruction of infrared images through the network was also verified in previous work [23-25].Perhaps not surprisingly,conventional deep-learning algorithms lack interpretability to some extent and heavily rely on abundant examples to train the network without incorporating any physical degradation model constraints[26-28].Each model training can only focus on a single situation-specific image reconstruction project and lacks the flexibility to cope with different tasks or different scale factors.To address the above issues,we propose an image-resolved algorithm based on the physical-model deep learning network,which is promising in regenerating high-resolution and non-honeycomb pattern images.In this research work,the primary options focused on the infrared radiation band,yet actual visible light images could also be employed.Based on this research work,it seems reasonable to pursue a similar set of fiber-optic bundle system configurations in future military research.

The remaining structures of this paper are as follows.Section 2 depicts the basic principle of our proposed method and presents the details of the proposed network for infrared fiber bundle superresolution.Abundant experimental results and analysis are demonstrated in Section 3.Finally,Section 4 enforces a discussion and summarizes the paper.

2.Methods

2.1.Theoretical analysis

The optical fiber image bundle is composed of multiple fibers,and each core conveys an individual image element.The current fiber bundle has a trade-off between the field of view and the core sampling rate.In order to combine the field of view and luminous flux of a single fiber,the diameter of currently manufactured fibers is empirically chosen to be slightly larger.The inherent fiber bundle physical limitation interrupts the information and weakens the imaging resolution,leading to a honeycomb pixelation (fixed pattern noise) of the sample.

In order to quantitatively investigate the correspondence between image quality and parameters of the optical fiber bundle imaging system,the concept of the average modulation transfer function (MTF) [29-31],commonly employed in the discrete sampling system,is introduced as the evaluation metric.The average MTF of the system can be indicated by the product of the Fourier transforms of each discrete sampling distribution function,which is expressed as follows:

where MTFsys,MTFobject,MTFfib,MTFrelay,and MTFdetectorrepresent the MTFs of the overall system,the fore-objective lens,the optical fiber imaging bundle,the relay lens,and the detector,respectively.The dual sampling of both fiber bundle and detector exists in the proposed system,and the imaging process of the fiber bundle includes low-pass filtering followed by the integral sampling of the fiber core and the discrete decimation of each fiber in the dense arrangement.MTFfibis composed of the fiber integral function MTFfib-intand the fiber sampling function MTFfib-sam.Therefore,MTFsyscan be expressed as

Among them,J1refers to the first-order Bessel function,dis the diameter of the fiber core,fis the spatial frequency,Δ represents the fiber core center distance,andprepresents the detector pixel size.

Our system adopts the chalcogenide glass infrared fiber bundle with a core diameter of 40 μm and a core center distance of 50 μm.Furthermore,infrared sensors with a pixel size of 15 μm and a center wavelength of 4.2 μm are chosen for data collection.As shown in Fig.1,under the premise of this invariant optical system,the system MTF mainly relies on the fiber bundle MTF.In this case,the cutoff frequency and spatial resolution of the system are not limited by the pixel size of the sensor or the diffraction effect.Instead,they are dramatically trapped by the fiber core center distance and core diameter (MTFfib).Due to the dual discrete sampling mechanism of the optical fiber bundle imaging system,honeycomb-like fixed patterns are imposed on its output images.In the optical imaging system,the multiplication of MTF in the frequency domain is equivalent to the convolution of the point spread function (PSF) in the spatial domain.The PSF (blur kernel) of the system is also a crucial indicator of imaging resolution capability.In light of the above analysis,the system degradation model is mainly affected by the fiber bundle,and the simulated blur kernel of the fiber bundle imaging system with the hexagonal structure is shown in Fig.1.The proposed method is also dedicated to solving the dilemma of incompatibility between sensor and fiber bundle sampling in fiber optic imaging systems.

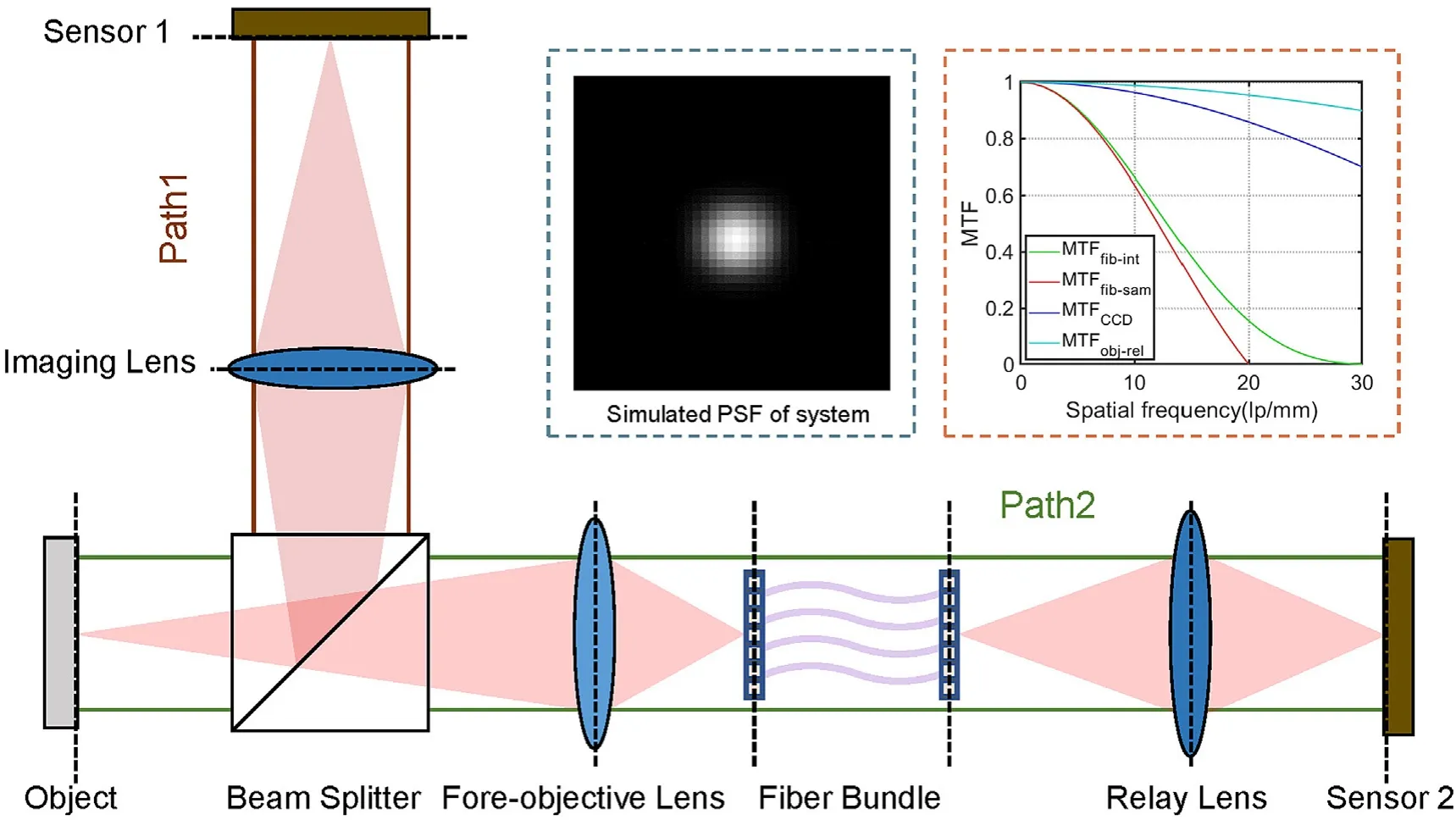
Fig.1.Schematic diagram of the dual-path imaging system.The blue dashed line illustrates the PSF of the simulated system,and the red dashed line represents the MTF of the simulated system.

The “one-to-one”dual-path imaging system is established to obtain HR images and degraded LR images simultaneously,as shown in Fig.1.To obtain the true observation image (label) and fiber image (input image) simultaneously,we introduced a beam splitter to split the light from the object into two paths.By physically adjusting the distance between the lens and the object,the image alignment error of the two imaging paths is at the sub-pixel level.Further,the post-alignment algorithm accomplishes the tiny alignment of the dual-channel images.

2.2.Proposed algorithm and network architecture

In this section,we investigate how to adapt the deep-learning method for honeycomb artifacts removal and far-field image restoration.As such,we resort to theoretical analysis and formulate the image restoration problem in a framework.Generally,image super-resolution is an inverse problem [32] where the objective is to recover the latent HR imagexfrom its blurred,decimated,and noisy observationy=SHx+n,whereSdenotes the standard down-sampler,Hrepresents the convolution operation with blur kernel,andnis the additive noise.The model-based deep learning method with degradation constraint is interpretable compared with conventional deep learning methods.According to the maximum a posteriori (MAP) framework,the HR image can be performed by solving the following optimization problem:

where μ is a regularization parameter associated with the quadratic penalty term,and such a problem can be solved via the following iterative scheme:

Mathematically,the data fidelity term and prior regularization term are decoupled into two individual subproblems,which can facilitate each other to realize blur elimination and detail recovery.Therefore,the model-based iterative network (MBIN) can be designed,whose framework consists of a data fidelity module and a prior regularization module iteratively.Fig.2 illustrates the overall architecture of MBIN withkiterations.

Fig.2.The overall architecture of MBIN with iterations k=8.MBIN consists of two main iterative modules,the data fidelity module to guarantee the solution complies with the degradation process and the prior regularization module to enforce desired properties of the output.

The data fidelity module imposes a degradation model constraint on the solution,which can be leveraged and incorporated into the network construct to guarantee more precise and reliable reconstruction.Specifically,the data fidelity module is related to a quadratic regularized least-squares problem which has various solutions for different degradation kernels.A direct solution is given by

We assume that the convolution is performed under circular boundary conditions.Hence,the fast Fourier transform can be adapted to efficiently implement Eq.(7).

For the prior regularization module,Eq.(6)can be reformulated as

Treatingzkas the“blurred”image,Eq.(8)minimizes the residue betweenzkand the “clear”imagexusing the prior Φ(x) [33].The corresponding minimization function is also named the so-called loss function.The latent mapping between “blurred”and “clear”maps can be learned by training the prior module,which acts as a detail enhancer for high-frequency recovery.

Inspired by the prior knowledge in information optics,we may impute the expansion of high-frequency components to the image prior rooted in the elaborately designed architectures.Physicsinformed learning seamlessly incorporates both data and mathematical models to address the under-determined problem,even in noisy and high-dimensional contexts.In fact,the physical prior was integrated into the forward generation process in earlier investigations.The optimized values of the physical prior are derived by gradient descent applying a back-propagation algorithm of derivatives,which is akin to the deep learning optimization process.

The process of cross introducing the optimization iterations of the physical model together with the fitting function of deep learning will significantly strengthen the interpretability of the network.Notably,in Fig.2,we introduce the physical iterative process and further incorporate the system's PSF into the network model.Quite the contrary,if only end-to-end learning is done without any physical model intervention,the image quality will undoubtedly suffer degradation.In previous super-resolved reconstruction projects,numerous efforts neglected the introduction of physical models as the most critical aspect.

U-Net,widely formed in multi-scale image-to-image transforms,is adopted to construct this module.As illustrated in Fig.2,the fundamental structure of the prior regular module involves a contractive branch and an expansive branch with four folds.Moreover,the module takes advantage of Resnet [34] to enhance network capacity and performance by introducing residuals.A set of two residual blocks are integrated on each scale of the branch[35],as shown in Fig.2.Specifically,the number of channels from the first scale layer to the end layer is set to 64,128,256,and 512,respectively,in that order.For the down-sampling and up-sampling operation in the contractive and expansive branch,we adopt 2×2 stridden convolution (SConv) and 2 × 2 transposed convolution(TConv),respectively,which are not followed by the activation function.In addition,skip connection can not only transfer image feature information but also alleviate the problem of gradient disappearance,enabling convenient transmission of valuable information in the network.In respect of the loss function,we adopt theL2loss to evaluate the peak signal-to-noise ratio (PSNR) performance.In the network,the batch size is set to 48.Adam solver[36] is adopted to optimize the parameters with the learning rate initialized as 10-4.The hardware platform of the network for model training is Intel Core™i7-9700 K CPU 3.60 GHz equipped with the RTX2080Ti graphics card,and the software platform is PyTorch 1.6.0 under the Ubuntu 16.04 operating system.

3.Experimental results and analysis

3.1.Dataset preparation

For the validation of our proposed method,the dataset is prepared by simulations,which dispenses with the available extra imaging system to provide well-registered pairs of fiber bundle images and their corresponding ground truth data.To obtain the LR counterpart from each mapped HR image,we impose the PSF for each hexagonal arranged core to the mapped HR image.The convolution operation of PSF,followed by the down-sampling operation,implements a weighted sum of HR pixels to yield an LR image pixel.

In recent years,deep learning is emerging as a powerful tool to address problems by learning from data,largely driven by the availability of massive datasets.Unfortunately,such simple degradation models could not faithfully describe the complex degradation processes in the real world.This motivates us to build a realworld SR dataset to narrow the synthetic-to-real gap.Our training data set consists of 1000 paired LR-HR images and their corresponding ground truth data.To monitor the accuracy of the neural networks on data never seen before,we created a validation set by setting apart 50 images from the original training data.A representative dataset in our proposed network is depicted in Fig.3.Note that our proposed network is still based on supervised learning.We consider the training process of the network as the task of learning the image prior,including fiber fixed noise,luminance bias,frequency characteristics,etc.The network attempts to recover an estimate of the envisioned sample from the degraded image by prior mapping knowledge (e.g.,the system transfer function).Therefore,a sufficient variety of images should be included in our datasets to construct the network mapping function as much as possible.The reconstruction process of the network is also not a magic trick,which requires a sufficient amount of prior information to support the fitting process of the parameters.Only when the dataset is guaranteed to a certain extent the nonlinear mapping will perform well in a massive sample.

Fig.3.A representative dataset in our proposed network.

For the data collected from the dual-path imaging system,HR images captured from Sensor 1 have the same pixel dimensions of 1024×1024,while LR images recorded by Sensor 2 are cropped to 256×256 pixels from 640×480 pixels.The end-to-end networks demand that LR images are interpolated to the same size as HR images,and image pairs are aligned by sequentially applying coarse and fine registrations for the network to learn the direct mapping relations.When using experimental data as ground truth,the reconstructed performance is inevitably contaminated by noise.Geometric changes such as rotation,translation,and deformation are implemented in images by finding inter-image feature points to eliminate the distortion errors between different lenses.When the distortion error is eliminated,we consider that coarse registration can be regarded as finished,and only the displacement between pixel levels remains for the registration error with respect to two images.Consequently,the frequency domain cross-correlation method [37] is adopted for precise registration to achieve subpixel error correction between image pairs.Considering the invariant characteristics of the imaging system,we could complete the registration of all datasets by performing only one-time coarse and fine registration,as shown in Fig.4.

Fig.4.Schematic diagram of the dual-path image alignment processing.

3.2.Quantitative evaluation based on the USAF resolution target

A USAF resolution target was employed to quantitatively validate the performance of the proposed method in terms of image resolution.Depending on the system parameters mentioned in Subsection 2.1,the forward model of the system is simulated with explicit degradation to acquire LR-HR image pairs in Subsection 3.1.The cellular fiber image in Fig.5(a) is generated from the original high-resolution infrared image,which is shown in Fig.5(e),through the dual discrete sampling of the fiber bundle imaging system.Figs.5(b)-5(d) presents the reconstructed results using U-Net,super-resolution convolutional network (SRCNN) [38],and MBIN methods,respectively.It is clearly observed from Fig.5 that the MBIN method addresses nearly all the major limitations of the other methods.

Fig.5.Comparison of U-Net,SRCNN,and MBIN on the synthetic USAF resolution target:(a)Input USAF target image;(b)-(d)Reconstructed images respectively used U-Net,SRCNN and MBIN methods;(e)Original USAF target image(ground truth);(f)-(h)Zoomed-in images of the region of interest(ROI)in(b)-(d);(i)Cross-sectional profile of dash line shown in (b)-(d).

Although all methods exhibit removal of the honeycomb patterns,images reconstructed by U-Net and SRCNN still survive with distinct pixelated patterns along the edge of bars,where the recovered edges are jagged rather than smooth.On the contrary,MBIN eliminates these artifacts along edges,maintaining uniformity in intensity closer to the original image.As shown in Fig.5(a),the minimum line pairs that can be resolved in the synthetic image is the element of the third group on the left,with a corresponding line width of 0.92 μm.To intuitively compare the performance of the three methods,we intercept regions of the rectangular box for comparison,as shown in Figs.5(f)-5(h).Note that results reconstructed by U-Net and SRCNN are blurred,and line pairs cannot be distinguished in the zoomed-in area.

Obviously,high-resolution images can be effectively reconstructed using our proposed method,and more specifically,our method can enhance the original resolution to the third group on the right,corresponding to a line pair resolution of 0.54 μm.The proposed method extends the imaging resolution to 1.7 folds,successfully breaking through the imaging resolution limited by the physical size of the original intrinsic system.Furthermore,we can be surprised to observe that the intensity profile of MBIN in Fig.5(i)achieves the best performance in both contrast and resolution.Evidentially,the proposed MBIN demonstrates apparent advantages in terms of linewidth and sharpness exhibited in the reconstructed image.

3.3.The network performance on real datasets

To further demonstrate that the proposed MBIN indeed improves the image performance,we conducted real scene data experiments with the dual-path imaging system.For the sake of efficient learning of the end-to-end mapping relations,except for the interpolation and registrations mentioned in subsection 3.1,the LR images are pre-processed with background noise reduction and infrared image enhancement before feeding into the network model.We compared the MBIN with two state-of-the-art restorative neural networks to verify the network's performance capabilities.In Fig.6(a),the patterns are partial images captured by the system oriented to the blackbody radiator and different hollow boards.The soldering iron and the tank model belong to selfheating objects directly recorded by the system.Obviously,these results indicate that all three methods could exhibit favorable performance in recovering the hidden information from the honeycomb patterns,whereas the high-frequency edges of the restored images obtained by U-Net and SRCNN are blurred.In contrast,sharper images reconstructed by MBIN distinguish finer details.We plot the average loss value and the average PSNR value for the validation dataset against the training epoch number of MBIN in Fig.6(b).Such two curves oscillate in the early epochs and converge stably after more training epochs.

Fig.6.(a)Comparison of fiber bundle image reconstruction;(b)The average Loss value and average PSNR value of the validation dataset against the number of training epochs;(c)The dual-path imaging system.

In order to further quantitatively evaluate the results obtained by different methods,the PSNR value and the structural similarity(SSIM)value are calculated for each reconstructed image relative to the corresponding ground truth,as listed in Table 1.It is obviously desirable that MBIN has the highest metrics values in all cases.Specifically,it shows superior performance in both SSIM and PSNR,which are,on average,5% and 5 dB greater than other methods,respectively.Perhaps not surprisingly,the principle behind this result is that the proposed network removes the honeycomb patterns effectively,and the hidden details are restored extremely similar to their ground truth,with higher PSNR and SSIM values representing more satisfactory results.

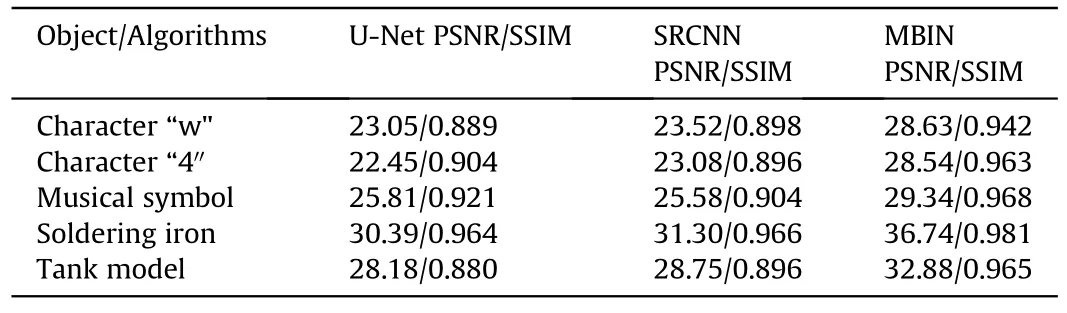
Table 1 Measurement of different reconstruction methods on PSNR/SSIM.

In the practical engineering application,multiple sub-eyes of the single-aperture fiber bundle can be arranged in the form of a compound eye array to capture multiple images at the same time,achieving high resolution and large field of view simultaneously by stitching multiple adjacent images with overlapping regions.Based on the super-resolution reconstruction method in this paper,the 2 × 1 compound eye array system with infrared fiber bundles is established.The system can be shifted horizontally to physically scan corresponding areas of the hollow board in front of the blackbody radiator continuously for acquiring 2 × 5 sub-images.Following that,a large-field image of the target is obtained by stitching sub-images,as shown in Fig.7,expanding the horizontal field of view angle from 21.48°to 65.31°.

Fig.7.Stitching results based on the fiber bundle and corresponding sub-eye images.

4.Conclusions

We have established and investigated a computational compound-eye imaging system with super-resolution reconstruction.The real-world infrared fiber bundle images and their corresponding ground truth images are both generated by the development dual-way imaging system.Image registration and rectification algorithms are developed to progressively align the image pairs.The constructed dataset can address the real-world image super-resolution problem with better performance.We also find that with the aid of introducing a physical model-based network,the solution can be incorporated to preclude some disturbing terms in the ill-posed inverse problem and possibly comply with the imaging model.As such,we gain insights into questions concerning image restoration problems.Finally,simply utilizing larger dimension imaging sensors and coordinating with multiple sub-eye images could,in principle,further push the imaging field of view and spatial resolution.The proposed MBIN method promises to enable new measurement opportunities for military defense detection and evolve our knowledge in the photoelectric detection field.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors would like to acknowledge the National Natural Science Foundation of China (Grant Nos.61905115,62105151,62175109,U21B2033),Leading Technology of Jiangsu Basic Research Plan (Grant No.BK20192003),Youth Foundation of Jiangsu Province (Grant Nos.BK20190445,BK20210338),Fundamental Research Funds for the Central Universities (Grant No.30920032101),and Open Research Fund of Jiangsu Key Laboratory of Spectral Imaging &Intelligent Sense (Grant No.JSGP202105) to provide fund for conducting experiments.