Satellite breakup behaviors and model under the hypervelocity impact and explosion: A review

Si-yun Ren ,Zi-zheng Gong ,* ,Qing Wu ,** ,Gung-ming Song ,Qing-ming Zhng ,Pin-ling Zhng ,Chun Chen ,Yn Co

a Beijing Institute of Spacecraft Environment Engineering,China Academy of Space Technology,Beijing,100094,China

b State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing,100081,China

Keywords:Satellite breakup Space environment Distribution characteristics Hypervelocity impact Explosion

ABSTRACT The primary causes of satellite breakups are hypervelocity impact and explosion,the research on satellite breakup can be used not only to evaluate the influence of breakup event on the space environment,but also to trace whether the satellite has been deliberately attacked.It is of great significance in both civil and military aspects.The study of satellite breakup behaviors and model is reviewed to summarize the research progress and insufficiency in recent decades,including the satellite breakup experiment,measurement and characterization of fragments,distribution characteristics of breakup fragments,satellite breakup model,etc.The classical studies are introduced in detail,and the limitations of the current research are pointed out.According to the current research results,the contemporary challenges and future directions for satellite breakup study are presented.The research on satellite breakup is developing in two directions: the miniaturization of satellite size and the complexity of satellite component.The study on satellite breakup needs to be explored and deepened on improving the experimental launch speed,expanding the model application range and breakup revealing the results under combined effect of impact and explosion.

1.Introduction

Since the first satellite was launched in 1957,more than 560 times spacecraft breakup events occurred by 2021,and debris from spacecraft breakup accounted for more than half of all cataloged debris.A satellite breakup is the usually destructive disassociation of an orbital payload,rocket body,or structure,often with a wide range of ejecta velocities,whereas a non-catastrophic collision only results in minor physical damage to the target [1,2].As a general rule,a satellite breakup will produce considerably more debris,both trackable and non-trackable,than an ordinary impact event.As shown in Fig.1,the causes of satellite breakup are mainly due to impact and explosion,or a combination of the two,including accidental and deliberate [3,4].The impact can be the result of an intentional intercept with kinetic energy weapon or the result of a random collision with space debris.The explosion may be caused by abnormal residual propellant and battery,and the impact may also cause incidental internal explosion,which is essentially the combination of impact and explosion.

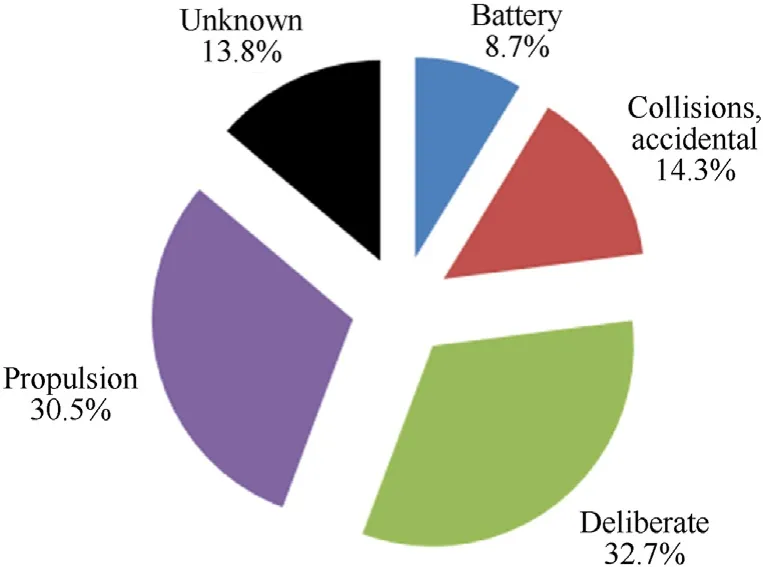
Fig.1.Proportion of cataloged satellite breakup debris remaining in orbit [1].

In 2021,mankind had carried out 114 space launches.As shown in Fig.2,with the substantial increase of space activities,the space environment has deteriorated sharply.In particular,the large-scale development of the LEO constellation satellite will increase the probability of explosive growth in the number of the orbital debris[6].The impact of millimeter sized space debris will cause perforation on the satellite surface and cause some functions to fail,but the satellite may still retain its remaining functions and continue to work in orbit.Due to the low detectability of centimeter size space debris[7,8],it is difficult for satellites to maneuver in orbit to avoid its impact.Once the centimeter sized space debris collides with the satellite,the huge kinetic energy will lead to the satellite breakup ASAT tests have led to the breakup of the satellite,and satellite breakup caused by ASAT are more serious than those caused by debris impact.Many countries have conducted many anti satellite tests to develop and test their ASAT capabilities.

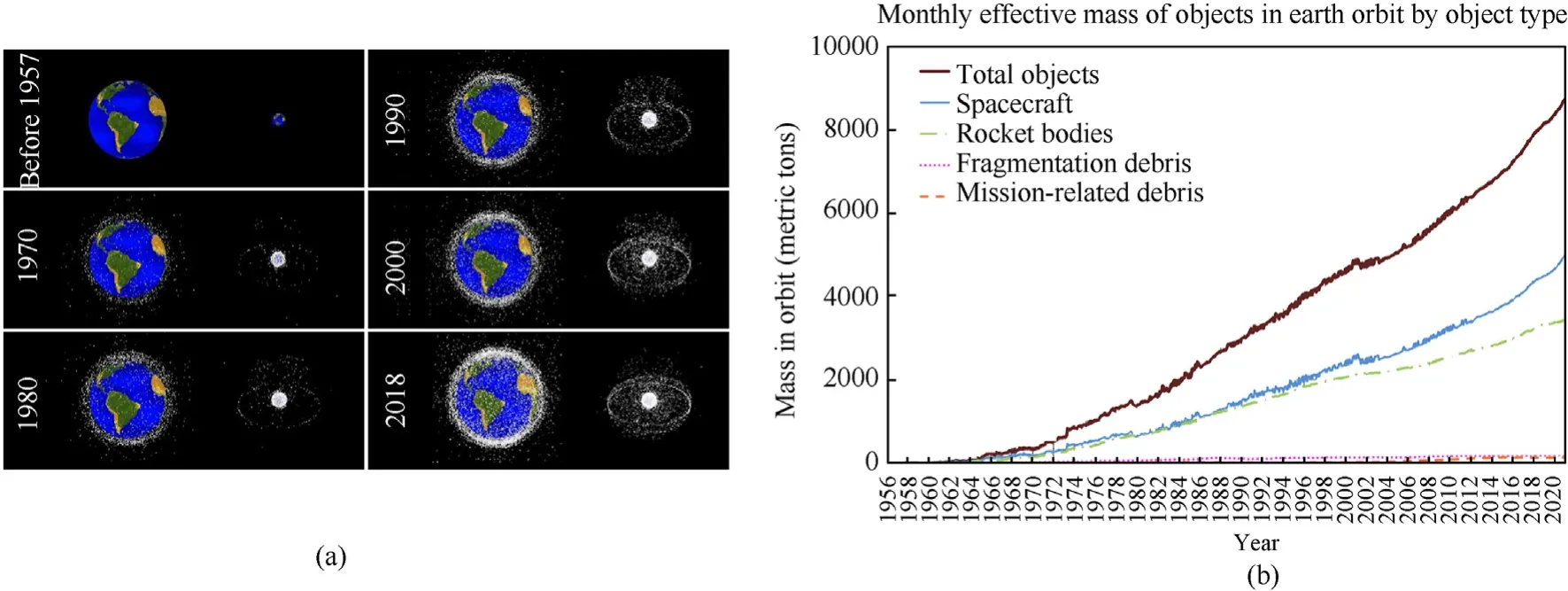
Fig.2.Space debris growth in different orbits and space debris mass growth: (a) Space debris growth in different orbits;(b) Space debris mass growth.

In previous satellite disintegration events,explosion was the primary cause,and note that a largest category of breakups consists of propulsion-related explosions.Breakup can be caused by accidental explosion caused by residual fuel and battery or deliberate explosion for the purpose of satellite self-destruction [13].On February 2015,a Defense Meteorological Satellite Program(DMSP)satellite of United States experienced a single breakup event induced by battery explosion,the resulting debris were so widely dispersed that extended more than 300 km above and below the pre-breakup orbit [14,15].In addition,most of the breakup events caused by deliberate explosions were due to the self-destruct of[9].In February 2009,the operational communication satellite Iridium 33 of the United States and the decommissioned communication satellite Cosmos 2251 of Russia collided at an altitude of 790 km with a relative velocity of more than 11 km/s,resulting in the breakup of both satellites[10].This event produced more than 800 large fragments that can be cataloged and identified and countless small fragments that cannot be cataloged and identified.In March 2021,the China's meteorological satellite YunHai 1-02 was collided by a mission-related debris associated with the SL-16 launch vehicle for the deployment of Cosmos 2333 in 1996,which led to the breakup of YunHai 1-02 [11].

Deliberate actions,often associated with activities related to national security.Military purpose was one of the main causes of deliberate breakup events.With the acceleration of space militarization,countries are competing to carry out anti-satellite (ASAT)tests in order to fight for the space control power,and the high probability results of collision of kinetic energy anti-satellite (KEASAT) weapons with satellites are breakup.Fig.3 shows the mission sequence of a typical multistage kinetic energy antisatellite weapon.Many of the early ASAT weapons relied on nuclear warheads or those with very high explosive yield due to the inherent inability to precisely target satellites moving at high relative velocity[12].With the progress of guidance technology,the modern ASAT weapons represented a significant improvement over earlier ones insofar as it employed a kinetic-kill mini-warhead to directly impact the targeted satellite versus an area weapon,and this is direct-ascent anti-satellite weapon.Since the mass of the warhead is much larger than that of space debris and the relative velocity of the warhead and the satellite is very high,most of the military satellites.

Fig.3.The mission sequence of KE-ASAT missile.

The satellite breakup events will have a significant influence on the space debris environment.The debris generated by the breakup events have accounted for more than 50% of the total cataloged debris,which poses a serious threat to other spacecrafts.The studies for satellite breakup can evaluate the risk severity caused by the breakup event,input the space environment model [16,17],provide impact early warning for spacecraft,and be used as the basis for design of spacecraft protective structure [18].In the military aspect,the studies for satellite breakup can be used to evaluate the damage effect of kinetic energy weapons on satellites,provide reference for the design of kinetic energy weapons.In addition,it can also be used to judge whether the satellite has been deliberately attacked and the type of intruder.This paper reviews the study on the breakup behaviors and breakup model of satellite under the hypervelocity impact,and introduces ground-based experiment,numerical simulation and theoretical modeling methods for satellite breakup.The classical studies are introduced in detail,and the limitations of the current research are pointed out.According to the current research results,the contemporary challenges and future directions for satellite breakup study are presented.

2.Satellite breakup experiment

2.1.The tests on orbit

ASAT tests were mainly used to test the effectiveness of ASAT weapons in destroying satellites,kinetic warhead impact and satellite short-range explosion were two main previously tested methods to destroy satellites.ASAT weapons launched into space generally fall into one of two categories: direct-ascent kinetic energy weapon or co-orbital systems.Direct ascent systems use rockets to put an interceptor on a suborbital trajectory that intersects with the target in orbit without the interceptor entering orbit itself,and most interceptors of this weapon are fragment warhead or kinetic energy warhead.By contrast,co-orbital systems use the Space Launch Vehicle (SLV) to place the interceptor into orbit,after which it maneuvers to pass near the target and destroy the target by explosion,and the most common interceptors of this weapon is satellites carrying high explosives.To verify the ASAT advanced technology,United States [19-22],Soviet Union/Russia[23-25] and India [26] have successfully carried out anti satellite tests,as shown in Table 1.In addition to testing and developing ASAT capabilities,the ASAT tests can also provide the new,unexpected,most intuitive and real scientific data for the study of satellite breakup.Such as,NASA used the results of Solwind P78-1[19]and Delta 180 [20] ASAT tests to modify the standard breakup model.The most recent ASAT test was that Russia destroyed a decommissioned military reconnaissance satellite Cosmos 1408 using a direct-ascent KE-ASAT weapon in November 2021[27],and the test produced more than 1500 traceable space debris and may produce hundreds of thousands of smaller space debris,which triggered an emergency response aboard the ISS [28],as shown in Fig.4.

Table 1 ASAT tests conducted by some countries [19-26].

The results of orbital breakup are generally obtained through ground telescope and radar observation,but only the data of larger breakup fragments can be obtained.Therefore,the observation orbital results of breakup can not reflect the fragments distribution within the whole size range,only part of the size range.The results of orbital breakup still play an important and direct role in verifying the breakup model within the observable size range.

2.2.Facilities and experiments based ground

2.2.1.The experimental facilities based ground

Many countries have conducted on orbit ASAT tests many times,which reflects the real satellite breakup results.However,the cost of such tests is very high,and the results also rely on the ability to observe and detect fragments.The experiment based ground is the most direct means to study breakup behavior.The small mass projectile can only cause a local perforation,and a debris cloud is ejected into the satellite and can produce damage to internal equipment,which can lead to a failure of critical components.This non catastrophic impact will not cause the disintegration of the satellite,but local damage.Satellite disintegration is a catastrophic event,in which the projectile mass (and hence impact energy) is large enough to produce the complete fragmentation of the satellite.High mass projectile impact is essential for satellite breakup,and it depends on large caliber loading facilities to drive the highmass projectile to obtain high velocity.

Arnold Engineering Development Complex (AEDC) conducted lots of satellite breakup tests utilized AEDC’s Range G light-gas complex [29,30] to support development of satellite breakup models of US Department of Defense (DOD) and National Aeronautics and Space Administration(NASA),which is capable of firing projectiles weighing more than 500 g up to 7 km/s,and such launch capability is extremely amazing and excellent,as shown in Fig.5(a)[31,32].China Aerodynamics Research and Development Center(CARDC) have a two-stage light-gas gun with the capability to launch massive projectiles for satellite breakup experiments.The two-stage light-gas gun was equipped with 25 mm,50 mm,120 mm and 203 mm caliber launch tubes [33-35].The gun can launch 1.43 kg projectile to the velocity of 6.34 km/s using 120 mm caliber launch tube[36],as shown in Fig.5(b).The two-stage lightgas gun of Kyushu Institute of Technology (KIT) can launch 40 g spherical projectile to the velocity of 1.5 km/s and 14 g projectile to the velocity of 4.5 km/s[37,38].The two-stage light-gas gun of Ernst Mach Institute(EMI)was also used in the study of satellite breakup caused by impact,and the gun can accelerate 3.7 g projectile to the velocity of 1.9 km/s[39,40].The 30 mm caliber two-stage light-gas gun of Beijing Institute of Technology (BIT) uses the detonation reaction of hydrogen oxygen mixture as the driving force,and the gun can launch 30 g projectile to the velocity of 5.63 km/s or 12 g projectile to the velocity of 8.38 km/s [41,42].

Fragments recovery is a complex and necessary work,and it must be achieved that all generated fragments are collected without any secondary damages to ensure the reliability of the breakup fragment data.The “soft catch”method with multilayer foam plates covering the target chamber was the widely used in satellite breakup experiments [43,44],as shown in Fig.6.

Fig.6.Fragments recovery methods: (a) The soft panel used to catch fragments in target chamber;(b) Fragments recovery box [43,44].

Although there are hypervelocity velocity loading facilities that have reached the ability to launch hundreds of grams of projectiles to 6-7 km/s,the launching capacity of all hypervelocity velocity loading facilities for large mass projectiles is less than 10 km/s,and the velocity of satellite in orbit collision may be as high as more than 10 km/s,which is a limit to the development of breakup model to a higher velocity range.

2.2.2.Ground-based tests

In order to gain insight into the general process and results of the disintegration of a complicated human-engineered structure on orbit,ground-based hypervelocity impact experiments were often used to reproduce breakup events.As shown in Fig.7(a),Bess[45](NASA Langley Research Center) conducted a laboratory experimental program to determine the amount of fragments produced and its size distribution when simulated spacecraft insulated fiberglass walls with a number of electronic boxes containing resistors and capacitors on the back were penetrated by hypervelocity projectiles.The results show that most of the fragments were irregularly shaped flat plates.Arnold Engineering Development Complex(AEDC)conducted 19 impact tests to study the damage of hypervelocity projectile to simulated satellite target [46],the simulated satellite targets were hollow cylinder and spherical Al tank,and the circuit boards were arranged inside the satellite target[47-49].The Part of the impact experiments of AEDC are shown in Table 2,the Energy-to-Mass-Ratio (EMR) is the impact energy to target mass ratio,and research shows that satellite breakup occurs when EMR is greater than 40 J/g [50].

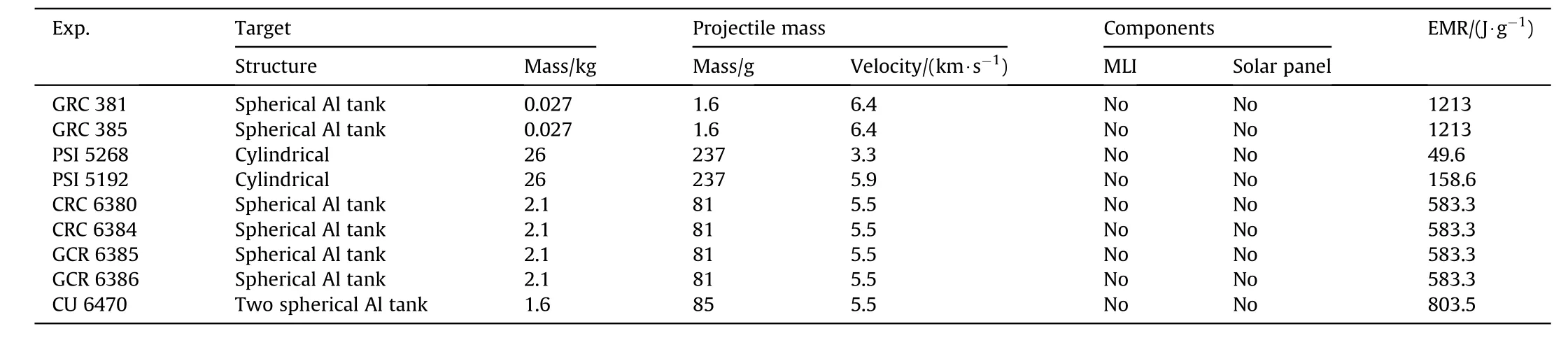
Table 2 Part of the impact experiments of AEDC [46].

Fig.7.Simulated satellite target in breakup tests:(a)Simulated satellite target of Bess tests;(b)Simulated satellite target of CARDC tests;(c)Simulated satellite target of EMI tests;(d) Simulated satellite target of Wang tests;(e) Simulated satellite target of Yu tests [51-56].

Lan and Liu (China Aerodynamics Research and Development Center,CARDC) [51-53],Schafer (Ernst Mach Institute,EMI) [54],Wang and Yu (BIT) [55,56] carried out hypervelocity impact and explosion breakup experiments on simulated satellite targets with single material (aluminum or steel) and simple structure (box or cylinder).The density distribution curve of area-to-mass ratio (A/M) of breakup fragments and the influence of residual fuel on the number of fragments were analyzed according to the experimental results,as shown in Fig.7(b)-Fig.7(e).It should be noted that the experimental results show that the energy density threshold value of 40 J/g is worth discussing.

It can be seen that the simple simulated satellite targets with the roughly similar structure used in the above experiments are far from the real satellite structure including battery,solar panel,circuit board,MLI and other components.Therefore,the experimental results can not truly reflect the distribution characteristics of fragments induced by the modern satellites breakup.US Department of Defense (DOD),National Aeronautics and Space Administration (NASA) and Arnold Engineering Development Complex(AEDC) carried out two famous series of breakup experiments:satellite orbital debris characterization impact test(SOCIT)and the modern satellite called DebriSat impact test [57] and the test utilized AEDC’s Range G light-gas complex.Table 3 shows the comparison of impact tests,and it is commendable that the projectiles used in these experiments were more than 100 g,and the impact velocities were higher than 6 km/s (see Table 4).

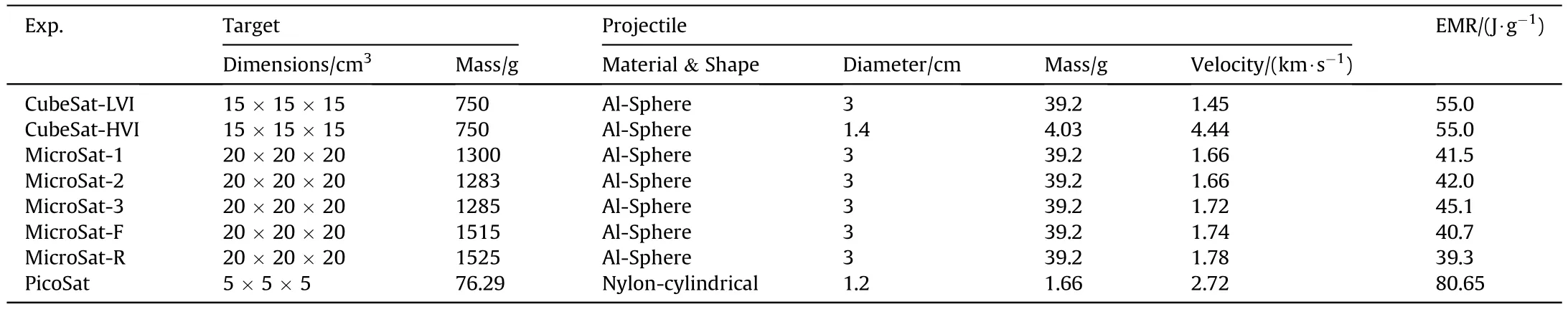
Table 4 The configuration of microsatellite breakup tests.

The SOCIT tests were a series of hypervelocity impact tests(four times) with test dates spanning from December 1991 to January 1992[58-60].The fourth test,SOCIT4,the target was a flight ready Navy Transit satellite made up of an octagonal core with a 46 cm diameter and a height of about 30 cm [61,62],which represented the typical structure of most satellites at that time,as shown in Fig.8(a) and Fig.8(b).The experimental results show that for a given characteristic length the fragments whose primary material was a metal appear to be consistently higher in mass than those whose primary material was a non-metal.The material of metal fragments was mainly aluminum,and the smaller the mass,the closer it is to spherical.By comparing the dominance regions of fragments with different shapes,it was found that phenolic/plastic blocks overwhelm all other shapes and materials in the regime below about 4 mm in characteristic length,as shown in Fig.8(c)and Fig.8(d).

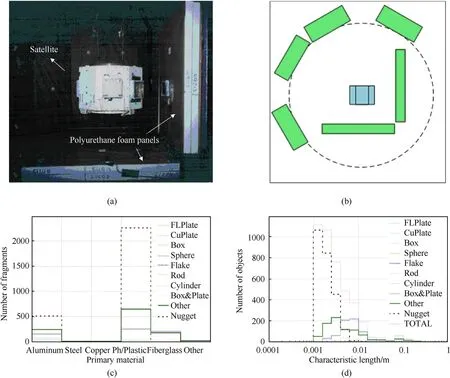
Fig.8.SOCIT4 experimental setup and results: (a) SOCIT4’s Oscar satellite;(b) Downrange view of foam panel configuration of SOCIT4;(c) Primary materials by mass vs.characteristic length;(d) The comparisons of the dominance regions of fragments with different shapes [61,62].

Although the satellite targets in SOCIT experiment are the real satellite,due to its old structure and few types of materials,there were obvious errors between the prediction results of the breakup model established based on the SOCIT experimental results and the modern satellites breakup event results[63].In order to update and expand upon the information obtained in SOCIT,the DebriSat project was carried out by NASA and the DOD [64-66],and the satellites were built using modern satellite materials and construction technology,as shown in Fig.9(a).Debrisat was built with components from a broad range of satellite mass classes [57],including coverglass interconnected cells (CIC),multilayered insulation(MLI),carbon fiber reinforced polymer structure(CFRPS),etc,as shown in Fig.9(b) and (c),Fig.9.Up to 14 materials are used in DebriSat,while SOCIT has only 6.

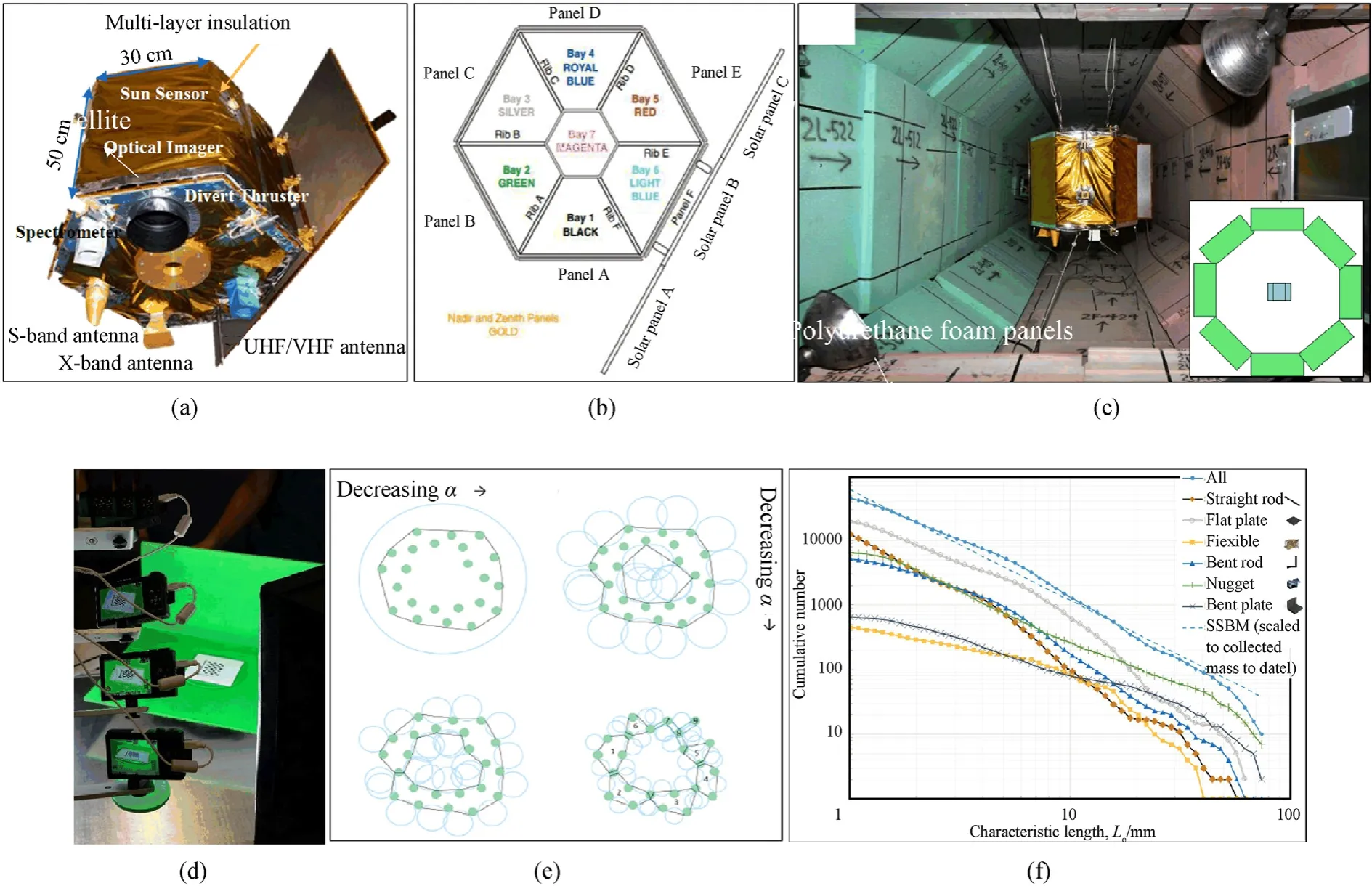
Fig.9.The design and experimental results of DebriSat: (a) DebriSat design;(b) DebriSat components;(c) Panels for debris collection in target chamber;(d) Space Carving technology;(e) Alpha shapes technology;(f) Cumulative number versus Lc as a function of the 6 shape categories used in DebriSat [57,63,65,66,69,70].

It is estimated there are 85,000 fragments larger than 2 mm in the collected DebriSat debris.It is commendable that the experiments used a variety of methods to measure and characterize fragments,such as x-rays,optics,radar,Space Carving technology and 3D scene technology,and the measurement results were used to estimate the material and size of the fragments [67-72],as shown in Fig.9(d) and Fig.9(e).The fragments are counted according to the material category and shape category,and the relationship between the Cumulative number and size of different types of fragments was obtained.The dominant material category and fragment shapes from different size ranges were obtained[73],as shown in Fig.9(f).

The size of satellite targets in the recent impact breakup tests was becoming smaller and smaller,and the composition was becoming more and more complex,including electronic,MLI,battery and other components.The variety of materials had become richer,which was closer to the satellites designed and manufactured with modern technology.As shown in Fig.10,Sakuraba,Hanada(Kyushu University)[44,74-77]and Lorenzo(University of Padova) [78] conducted a series of impact tests on microsatellites,and the effects of impact velocity,impact direction and fragment size on the distribution characteristics of breakup fragments were analyzed.The results show that there was similarity in mass distribution of fragments between low and high velocity impacts,and there were obvious differences in size versus mass distribution of fragments with different density [79,80].The breakup fragments from different impact directions were similar in size and mass distribution,but there were obvious differences in area to mass distribution [80,81].The area-to-mass distributions were affected by materials choice,which can affect the prediction accuracy of the breakup model [78].

Fig.10.Microsatellite breakup tests and results:(a)CubeSat target;(b)Breakup fragments of CubeSat tests;(c)Fragment distribution results of CubeSat tests;(d)MircoSat target;(e) Breakup fragments of MircoSat tests;(f) Fragment distribution results of MircoSat tests;(g) PicoSat target;(h) Breakup fragments of PicoSat tests;(i) Fragment distribution results of PicoSat tests [44,74,75,78-80].

The essence of satellite impact breakup is the failure of structure and connections caused by the propagation of shock wave along the structure,and this failure depends on the conversion of the kinetic energy of the projectile into the energy absorbed by the crushing,fracture and deformation of the materials.In addition to the impact,the breakup of the satellite may also be caused by the fuel/oxidizer explosions or pressure bursts of fuel tank [82],which may be caused by accident or impact,and the essence is structural failure caused by internal pressure surge or high pressure release [83].1986 the SPOT-1 Ariane third stage was violently separated into some 465 detectable fragments[84,85],and over pressurization of the rocket body from residual propellants might have caused the breakup [86,87],as shown in Fig.11(a).In order to study the explosion breakup of the upper stage of the launch vehicle,metal soft can (pressurized and unpressurized) [88,89],sealed stainless steel tube[90],water-filled tank[91],metal cylindrical casing with charge [92] are used to simulate rocket fuel tanks,as shown in Fig.11(b)-Fig.11(g).The experimental results show that the size and number of breakup fragments were closely related to residual fuel and tank pressure.AEDC and European Space Operations Center of European Space Agency(ESA)conducted high simulation hypervelocity impact and explosion tests on the scale model(DebriLV)of Delta upper stage tank and scale models of the Ariane H10 upper stage tank [93-95].Findings indicate that the vapor phase generated from the impact was a large contributor to much of the secondary damage on and around the test article,and all fragments from the explosion tests were plate-shaped.

Fig.11.Breakup tests of fuel tanks: (a) Ariane third stage;(b) Soft drink can used in Cour-Palais and Crews’s tests;(c) Sealed tank breakup test;(d) Explosion test of cylindrical casing charge;(e) Stainless steel tube breakup tests;(f) Impact tests on water-filled Ti-6Al-4V tanks;(g) DebriLV breakup tests [88-95].

A large number of experimental studies have been carried out on hypervelocity impact breakup,including the impact on real satellites.The research on satellite breakup is developing in two directions: the miniaturization of satellite size and the complexity of satellite component.As shown in Table 5,as the components and materials of satellites designed and manufactured with modern technology are more diverse,the breakup test results of satellite targets with more components and materials are closer to the real situation.The fragments data obtained from ground-based tests have a smaller size range than the data observed orbital breakup,can usually be counted to millimeter fragments,which can provide direct data for the wide range breakup model to predict the small sized fragments induced by orbital breakup.However,there are few explosion breakup tests on real satellite targets,and a large number of experiments were mainly aimed at the explosion breakup of rocket fuel tank.Most importantly,the current explosion breakup tests ignore the explosion caused by impact.In this case,the breakup of satellite is caused by the combined effect of impact and explosion.How the impact energy and explosion energy affect the fragment distribution and the difference between breakup induced by the combined effect of impact and explosion and simple impact or explosion breakup are urgently needed to be revealed through experimental study.

Table 5 Comparison of satellite components and materials used in breakup tests (Black dots represent yes).

2.3.Measurement and characterization of breakup fragments

After impact tests,all fragments(including fragments of devices for recycling) and dust were carefully collected,documented,and stored.Then the satellite fragments need to be picked out,measured and entered into the database.The subsequent fragment measurement and characterization of breakup tests has a vital impact on the fragment data analysis and the establishment of breakup model.The high-precision measurement of fragment characteristics (such as size,mass,cross-sectional area,etc.) is an important and time-consuming work[61,62].Because the satellite has a complex structure and a variety of materials to achieve a variety of functions,the characteristics of debris with different densities and materials have different distribution results after the disintegration of the satellite,and the fragments of satellite breakup needs to be counted according to various categories(such as material,shape and density).NASA approach visually classified fragments into flat plate,curled plate,box,sphere,flake,rod,cylinder,box and plate,nugget,other [96],as shown in Fig.12(a).In DebriSat test,2D and 3D imaging systems were used to reconstruct the geometry of fragments to obtain dimensions with an error of less than 1% [97,98],as shown in Fig.12(b) and Fig.12(c).

Fig.12.Measurement and characterization of breakup fragments:(a)Fragment shape categorization;(b)2D imaging and measurement;(c)3D imaging and measurement[98,99].

NASA developed radar Size Estimation Model (SEM) based on fragments from SOCIT tests [93],and radar could provide a radar cross section (RCS) at a specified frequency to estimate the fragment size and shape.The model is related to the radar detection frequency,and the size of the object can be obtained according to the RCS detected by the radar[99-101].The RCS of the same object observed by different radars and the same object observed by the same radar at different times will be different,which makes it difficult to estimate the size.According to DebriSat tests data,the optical measurement method depending on range,albedo,and phase function was developed to estimate the type of fragment material[102-104].Radar and optical measurement have practical significance,and can be applied to the fragment characterization and measurement in orbital breakup events.According to the SEM,the relationship between fragment size and radar RCS can be expressed as

where,Dis the fragment size,λ is the radar wavelength,z=RCS/λ2.g(z)is the interpolation function,which can be obtained according to the corresponding relationship table.

In the NASA standard breakup model,the characteristic length was used as the variable rather than the mass.Reynolds and Madler[105,106]proposed a calculation method of characteristic lengthLcto describe size,area,and shape for debris fragments in NASA standard fragmentation model.Lcis the characteristic length defined as the average of three orthogonal projection dimensions inx,y,andz,as shown in Fig.13(a) and Fig.13(b).

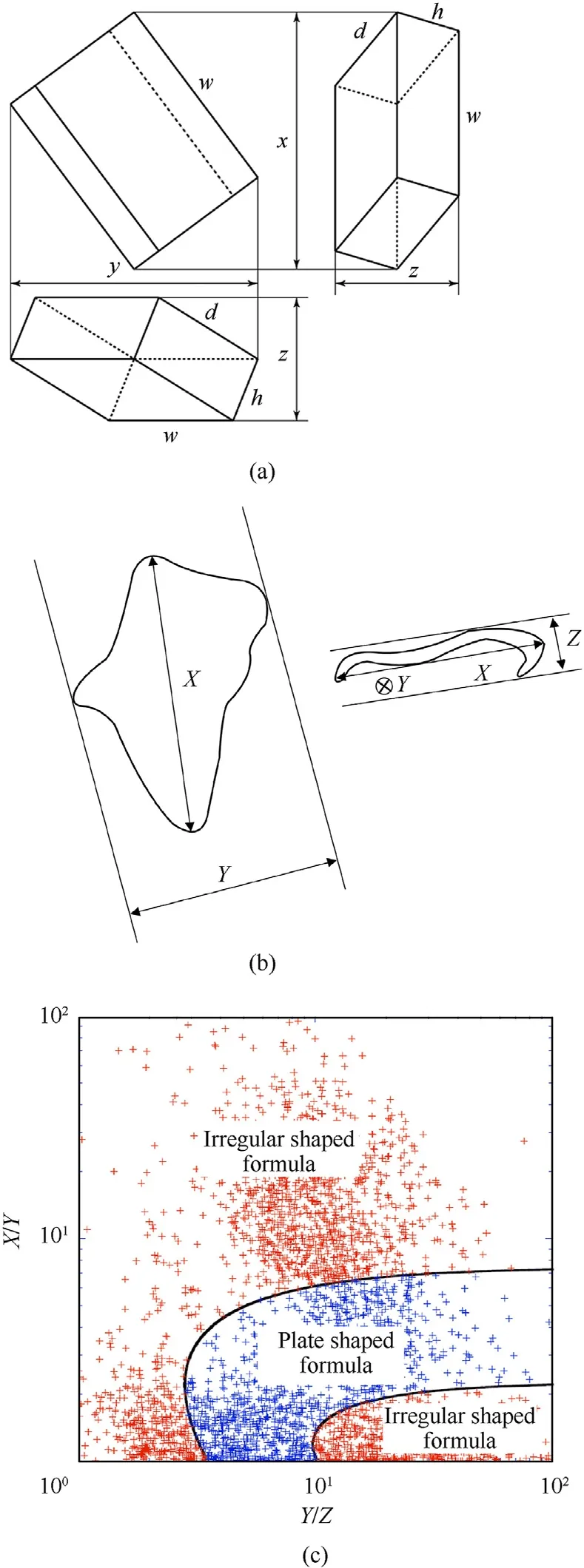
Fig.13.Fragment three orthogonal projection dimensions and shape regimes:(a)Ideal plate three orthogonal projection dimension;(b) Irregular fragment three orthogonal projection dimension;(c) Shape regimes of fragments from the CubeSat tests[105,106,108].

The approach to calculate the average cross-sectional area of breakup fragments is described in the NASA standard breakup model 1998 revision,and the approach was applied in SOCIT experiments [61].The procedure is to first determine the projected areas of the object in theX-Yplane(AX-Y),in theY-Zplane(AY-Z),and in theZ-Xplane (AZ-X),and then calculate the average crosssectional area as

HereXis the longest dimension,Yis the longest dimension in the plane perpendicular toX,andZis the longest dimension perpendicular to bothXandY[61].Since the cross-sectional area is described by the arithmetic mean of the three projected areas in Eq.(2),the prior shape classification in the three cross-sectional areas must be considered.The NASA approach proposes to calculate the average cross-sectional area of a plate-shaped(Including flat plate,curled plate,and flake as plates) fragment is as follow:

NASA considers other irregular fragments to be ellipsoids,whose cross-sectional area can be expressed as

Hanada and Liou[75,79]found that the A/M of needle fragments in CubeSat experiments is surprisingly high,and demonstrated that the a simple and general transition between irregular and plate shaped regimes could be expressed as a function of aspect ratio(X/Y)and thinness(Y/Z).The applicable regimes where fragments can be classified into irregular or plate shaped objects were illustrated as show in Fig.13(c).The NASA approach is highly sensitive to the aspect ratio,which leads to a drastic increase in estimation uncertainty with aspect ratio.The plate-shaped formula may overestimate the average cross-sectional area of thicker plates with a low value ofY/Z[107].The average cross-sectional area of needle fragments should be estimated by irregular-shaped formula rather than plate-shaped formula.It is precisely because NASA approach considered the needle fragments as cylinders that leads to the error of cross-sectional area estimation and makes the A/M of needle fragments too high.Hanada and Liou [108] proposed a new approach to estimate the average cross-sectional area of breakup fragments,Eq.(3) was still applied to estimate the average crosssectional areas of fragments appearing in the plate shaped regime,and Eq.(6) instead of Eq.(5) was applied to estimate the cross-sectional area of fragments appearing in the irregular shaped regime.The estimation formula and error can be expressed as

where,p～1.6075 yields a relative error of at most 1.061%.Irregular plate fragments should also be calculated according to the irregular shaped formula rather than using the plate shaped formula.

At present,the research results show that the characteristic length is obviously affected by the shape and density of the fragment material,resulting in the overestimation or underestimation of the A/M distribution obtained from the tests.The current solution is to use the formulas corresponding to different shapes to calculate the characteristic length of breakup fragments,and this method needs to use the value of size ratio in different dimensions to determine the shape transitions.It is necessary to develop a universal calculation method of fragment characteristic length to avoid the confusion caused by shape uncertainty.

3.Satellite breakup simulation

Considering that the satellite breakup tests close to the real event have many difficult factors,such as complex satellite target,high cost and large amount of data extraction,the combination of a small number of tests simulating real events and a large number of numerical simulations has become an efficient means to study the breakup fragments distribution characteristics.Currently hypervelocity velocity impact numerical simulation technique is mainly used in analysis for spacecraft shield against orbit debris,and the most widely used method is Smoothed Particle Hydrodynamics(SPH) [109-114].As shown in Fig.14(a),SPH was also used in the numerical simulation of satellite breakup[115],but it was difficult to identify individual fragments and the interface of material cracked and uncracked,because output of SPH simulation was usually discrete debris cloud.

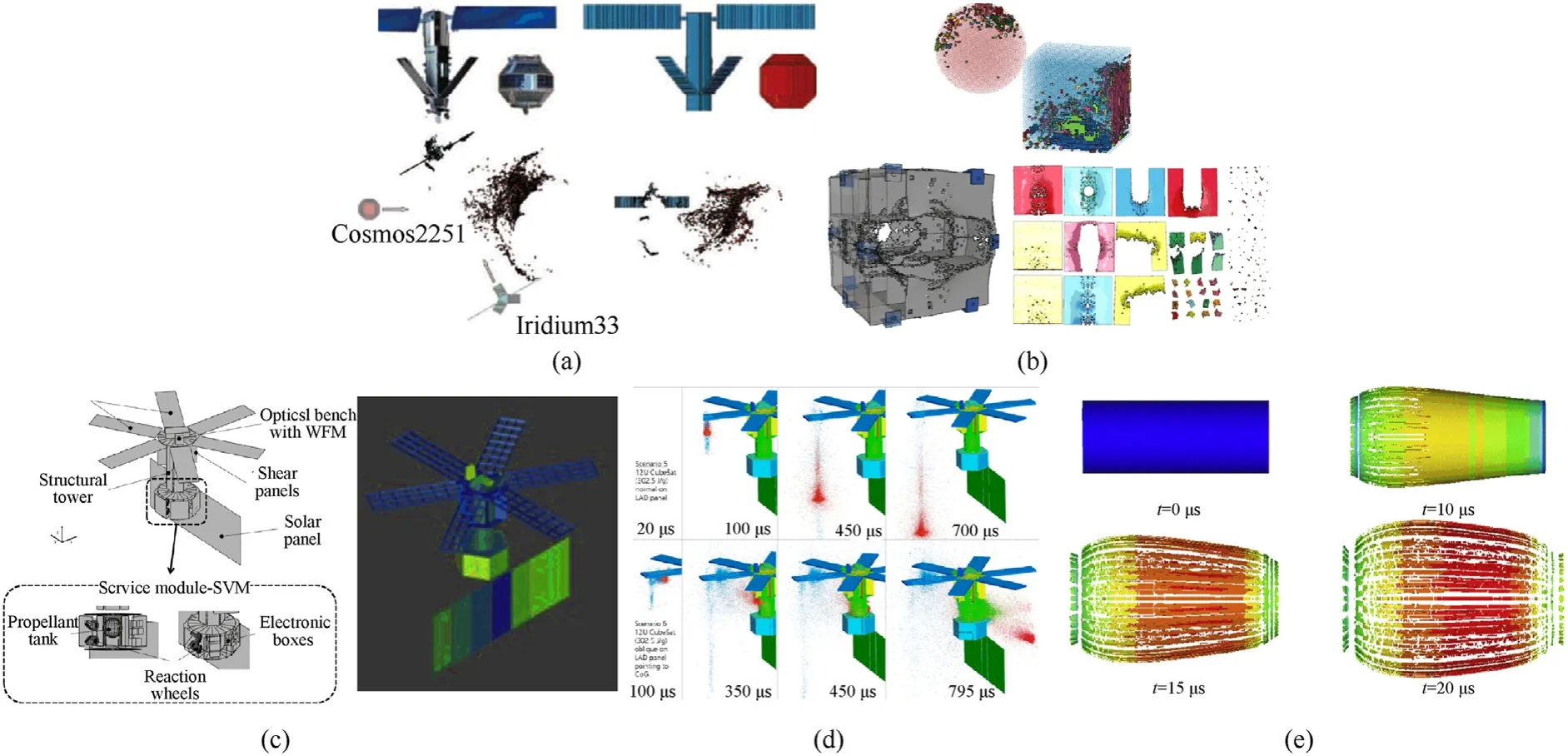
Fig.14.Numerical simulation of satellite breakup:(a)SPH method;(b)Finite element reconstruction method;(c)Collision Simulation Tool;(d)PHILOS-SOPHIA code;(e)Simulation of cylindrical casing fragmentation under explosive loading [115-119].

Zhang and Jia [116] presented a finite element reconstruction(FER) method for numerical simulation approach for spacecraft disintegration fragment analysis,and this is an improved based on hybrid method of finite element method (FEM) and SPH method[117],as shown in Fig.14(b).The cracked material was represented by particles and the uncracked material was represented by finite elements.FER approach can model the spacecraft and the impactor in detail including the shape,internal structure,material feature,impact velocity magnitude and direction,and also impact location,and the simulation results of large impactor impacting satellite show that different impact positions in the target will lead to various fragment characteristics.EMI and ESA [118] developed numerical simulation tool PHILOS-SOPHIA using the coupling of SPH and FEM,and the large-scale numerical simulations of the ESA LOFT satellite model colliding with small satellites in various collision geometries was performed to analyze the breakup criteria.The results show that the impact geometry and secondary debris impact have a great impact on the damage and fragment characteristics.Depending on the collision vector,impacts on the outer parts of a spacecraft may result in both higher and lower fragmentation in comparison with impacts on the center of mass,which cannot be reflected by simple breakup criteria based on EMR.ESA and University of Padova [119] combined the empirical data with the conservation principle to develop a new semi-empirical numerical simulation tool,and applied it to the numerical simulation of satellite breakup.The semi-empirical breakup models were applied to addressing individual fragmentation of macroscopic elements,and the discrete element method was used to simulate structural deformation,fracture and separation of satellite broken parts through the simulation of momentum transfer to macroscopic elements by a system-level net,taking into account energy dissipation inside elements and across links.The simulation results show that the same EMR will lead to different damage due to different impact positions,and it is also shown that the NASA model may overestimate the fragments distributions when impacts are not central and/or the ratio between impactor size and target size is small [120].

In order to study the distribution characteristics of fragments after warhead explosion,a large number of numerical simulation have been carried out on the explosion of metal cylindrical shell charge [121-124].According to simulated results,the fragment mass distribution,the initial fragment velocity,as well as the spatial and the shape distributions of fragments,enable the complete characterization of a fragmentation process [125-127].At present,the numerical simulation of satellite explosion breakup is still similar to the explosion of metal cylindrical shell charge[55,128,129],in which explosives were used to simulate the explosion of propellant.However,the explosion of propellant is not the same as that of explosive.Because the detonation velocity of explosive is faster than propellant,its explosion will produce higher internal pressure than that of propellant explosion,and the expansion of detonation products is faster than that of propellant explosion,resulting in faster breakup fragments.At present,it is difficult to simulate the coupling between the complex chemical reaction,energy release and product expansion of propellant and the subsequent structural response leading to satellite breakup.

Obviously,the hybrid method of FEM and SPH method can be used to describe structural failure and material fragmentation,but the selection of equation of state and constitutive model should be careful.At present,it seems that there is little research on the influence of constitutive model and equation of state on the distribution characteristics of disintegration fragments.The equation of state has an obvious effect on the melting and gasification of a considerable proportion of materials caused by hypervelocity impact,and the fracture and failure of structural is closely related to the constitutive model.In addition,it is very important to extract the fragment size in numerical simulation,and the material failure boundary need to be clarify to determine the fragment size.Therefore,the key to accurate statistics of fragment size in numerical simulation is to adopt a more accurate failure model.

4.Satellite breakup theoretical model

4.1.Energy density threshold

The catastrophic fragmentation and incomplete fragmentation of satellites are often distinguished by Energy-to-Mass-Ratio(EMR),which is defined as the event energy per target mass,EMR=E/mt(J/g).McKnight [130] in order to develop the FAST breakup model,it was confirmed that the energy density threshold for satellite complete fragmentation was between 35 J/g and 40 J/g based on the hypervelocity impact tests of AEDC,and the nominal value is 40 J/g,as shown in Fig.15.Since the value of EMR is much larger than the theoretical energy required for brittle and ductile fracture of materials,McKnight[131]believed that this is due to the poor energy coupling efficiency of complex structures under hypervelocity impact,and an energy coupling coefficientPwas added to describe the energy transfer efficiency at different positions of impact.ThePvalue depends on the correlation between the impact location and the satellite core mass,as shown in Fig.16(a).However,EMR is still for the satellite as a whole,and does not consider how energy is distributed among different structures and components within the satellite.Zaccariotto et al.[132] employed Statistical Energy Analysis(SEA)method to calculate how such energy is transmitted away from the impact location and then distributed to other spacecraft parts,as shown in Fig.16(b).How the impact energy is partitioned among some selected macroscopic structural components can be predicted and the minimum value of impact energy for which the part is fragmented (breakup threshold) of each component can be evaluated.The calculation results demonstrated that the satellite fragmentation process strongly influenced by the debris impact location,and the whole spacecraft breakup may be inhibited by the structural properties and junction discontinuities.

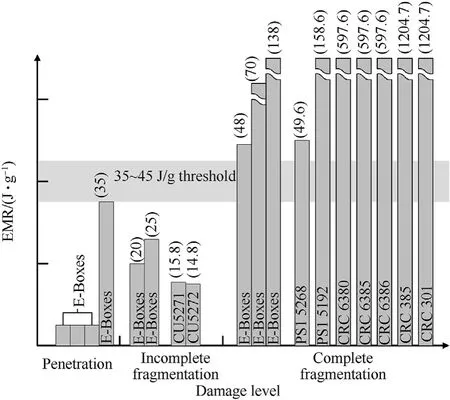
Fig.15.Damage level of satellites under different EMR and the energy density threshold [130].

Fig.16.Energy coupling coefficient of different impact point and energy flow between connected parts [131,132].

Liu et al.[33] found that the satellite did not completely disintegrate with the EMR was 113.24 J/g and 158.06 J/g far greater than 40 J/g through the experiment of impacting the satellite simulation target.Li et al.[133] believed that the ratio of the ratio of impact energy to the mass of the satellite participating in the breakup should be considered as the energy density threshold.This will cause the energy density threshold to be much greater than 40 J/g because the main wreckage after breakup was not counted into the mass participating in the breakup.

The essence of satellite breakup under projectile impact is the failure of satellite structure caused by the propagation of shock wave along the satellite structure and the impact of debris cloud induced by initial impact on the structure.Because the satellite is composed of multiple components connected and fixed together through connectors to form a whole with certain mechanical strength，the mechanical strength differences of different components and connectors between different components are different.Therefore,it is debatable to use an energy density threshold which ignoring the components and their connectors as the criterion of satellite disintegration.In addition,the influence of the projectile shape on the satellite breakup energy density threshold should be considered.

4.2.Satellite breakup models

Breakup model is used to describe the outcome of satellite or upper stage breakup caused by explosion or impact,and it can be used to simulate the generation of fragments[134,135].At present,most breakup models are semi-empirical models based on the results of experiments and orbit breakup events,due to the low applicability of empirical and theoretical models induced by low accuracy or too complex[136].Breakup model can provide data as space debris model to characterize of the orbital debris environment past,present,and future,which can provide short-term and long-term impact prediction and risk assessment for orbital spacecraft.The potential military application of the breakup model is to infer the source of attack according to the satellite breakup results.After years of research and development,a variety of satellite breakup models have been proposed,such as IMPACT breakup model,FAST breakup model,the Battelle breakup model for MASTER debris environment model,NASA standard breakup model and CARDC spacecraft breakup model.The satellite breakup model mainly includes mass/size distribution,area-to-mass ratio distribution and delta velocity distribution [137-139].

4.2.1.Mass and size distribution

In satellite breakup model,three ways of producing space debris have been considered: hypervelocity impact,low intensity explosion,high intensity explosion.The high-intensity explosion was defined as one in which an explosive charge is in contact with some part of the spacecraft structure,and explosions of this type produce many small fragments which cannot be tracked with ground-based radar.The low-intensity explosion is one in which an explosive charge is not in direct contact with any spacecraft structure,such as pressure vessel explosions.Mass and size distribution quantifies the results of breakup events by giving the relationship between the cumulative number and size or mass of fragments.It is the key to reliably predict the results of satellite breakup,and it is also the most basic distribution characteristics of breakup fragments.

4.2.1.1.Collision.Bess [140-142] presented the mass distribution model of breakup,and the mass distribution of collision was established based on the hypervelocity impact experimental results[45].

where,CNis the cumulative number of fragments with mass equal to or greater than somemf,mfis the mass of fragment,is the scaling factor along the cumulative number axis,Bdrives the slope of the mass distribution curve.TheAterms for the two tests were 7.32 and 4.06 respectively,theBterms were 0.80 and 0.84,respectively.

Kessler modified the mass distribution model by replacingmfwithfor collision [143,144].

where,meis the eject mass,me=vrel2mp,vrelis the relative velocity between the projectile and the target,km/s.A=0.4478,B=0.7496.Battelle breakup [145-147] model was employed for the previous MASTER debris environment model,with the update of MASTER version,NASA standard breakup model is used as the breakup object data source of MASTER.The mass distribution in the Battelle breakup model was described by the same power law as Eq.(9),and the calculation methods of coefficient were given as follows[148,149]:

where,mpis the projectile mass,vpis the impact velocity,mtis the target mass,Pf/tis the ratio of mass of the target participating in the breakup to target mass.

In order to analyze the Solwind P78-1 ASAT test results[19,150],the Aerospace Corporation developed the IMPACT satellite breakup model,which was later used for the analysis of Delta 180 ASAT test results [20].The IMPACT model [151,152] attempts to conserve mass,energy and momentum in breakups due to collision or explosion.Momentum conserved by forcing even number of fragments in each mass bin,and mass is conserved by iteratively summing all fragments and ensuring total mass is within a specified error.The collision mass distribution consists of a power law function to describe larger fragments while the fragments belowm=0.0015 kg follows an exponential function similar to that of explosion.It is worth noting thatis used instead of[137].

wheremc=0.0015 kg,mtotis the total mass of the target and projectile.The calculation method of coefficient was given[151,152].

where,mpis the original projectile mass,mtis the mass of original target vrelis the relative velocity between the projectile and the target.In the latest IMPACT 8.0 breakup model [153],only the power law was used to describe the mass distribution of breakup fragments.

McKnight [154,155] represented a parabola fitting results to improve the FAST model for simulations of satellite breakups from debris impact and for missile-interceptor theater-level engagements

where,C,D,andEare the constants,C=2.1-4.4,D=0.1-0.8,E=3.0-7.4.

The results show that,for power law,the values of constantsAandBdepend on the accuracy of statistical results.The error will cause the values of A and B to fluctuate greatly.Especially,becauseBdetermines the slope of the curve,the large error in small mass fragments will lead to very highB.Comparing to power law,Parabola has better fitting effect.The main difference between parabolic law and power law is reflected in the estimation of the number of small mass fragments,and the estimated number of power law is greater than that of parabolic law.

The mass distribution of CARDC spacecraft breakup model[156]used a power law function similar to Eq.(8)given by Bess,but the relationship between the coefficientsA,Band the impact velocity,energy density threshold and satellite average density were established.In particular,-Bis positively correlated with the lgv and lgρt.

where,ρtis the average density of satellite,is the impact velocity,emis the energy density threshold of breakup,μcis the breakup extent,whose value is equal to the ratio of the sum of the small fragments mass to the initial target mass,t1=4.7466,t2=0.4918,t3=0.3503.

In the previous NASA standard breakup model,fragments of a catastrophic collision followed two size distributions,a power-law distribution and exponential distribution [157,158].The distribution model based on the ground experimental data described the distribution characteristics by a function with mass as variable,because the mass is more intuitive and easy to measure.However,the fragment size more directly linked to both the on-orbit and terrestrial breakup data,revised NASA standard breakup model and the characteristic lengthLcis chosen as an independent variable in NASA standard breakup model based on SOCIT test results and one well observed Solwind P78-1 orbital collision event.As shown in Fig.17,the calculated results of cumulative number matched well with the experimental results of DebriSat tests,CubeSat tests and orbital observation data of breakup events [44,134,159],and the prediction results of NASA standard breakup model are in good agreement with the test results and the observed data of orbital breakup events.The size distribution is expressed as [160]:

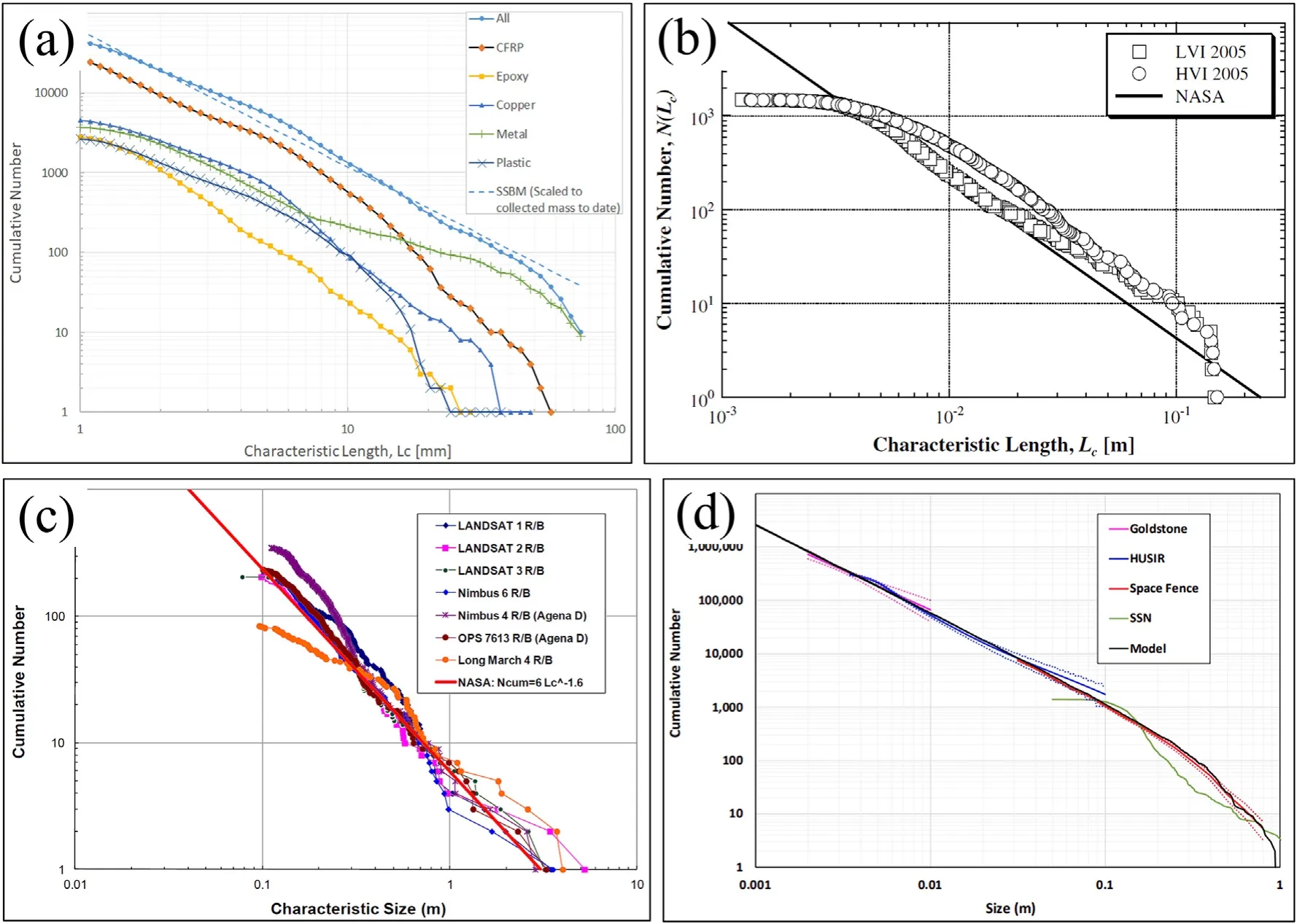
Fig.17.Comparison of calculated results of size distribution in NASA standard breakup model with test results and observation data of orbital breakup events [44,134,159].(a)Comparison of NASA standard breakup model size distribution and DebriSat tests fragments;(b)Comparison of NASA standard breakup model size distribution and CubeSat tests fragments;(c) Comparison of NASA standard breakup model size distribution and observation data of seven satellite breakup events in orbit;(d) Comparison of NASA standard breakup model size distribution and observation data of Russian Cosmos 1408 ASAT test in 2021.

According to the low velocity impact experiment [161,162],Hanada extended the NASA standard breakup model to the velocity range of hundreds of meters per second to predict the low-speed collision in geostationary orbit.The size distribution of the experiment can be well described by the slope of Eq.(23).Therefore,the NASA size distribution model was modified towards the greater size range by replacing the coefficient 0.1 in Eq.(23) with 0.6 to describe the size distribution of low velocity impact [163].This shows that the coefficient of size distribution may be related to the impact velocity rather than a fixed value,which can be reflected by taking an expression with velocity as a variable as a parameter of size distribution by further study.

Although the size distribution in NASA standard breakup model was widely used,the mass distribution was still indispensable.The total number of fragments can be calculated according to the mass distribution and total mass of projectile and target to ensure the conservation of mass in breakup[164].In addition,according to the experimental results,the relationship between mass and size is obviously affected by material density[61,80,108,159],which shows that the mass of fragments with the same shape and size and different density is different.This will lead to wrong estimation of A/M of fragments with a certain size.As shown in Fig.18,it can be seen from the results of different tests that multiple material density groups can be distinguished in the size/mass relationship.Obviously,the size/mass relationship of fragments with different densities cannot be described by the same curve.Real satellites are made of components composed of different materials,and breakup fragments have a variety of densities.This fact leads to the improvement of the breakup model considering material density[80,160],which can make the calculation results of the breakup model closer to the real situation.

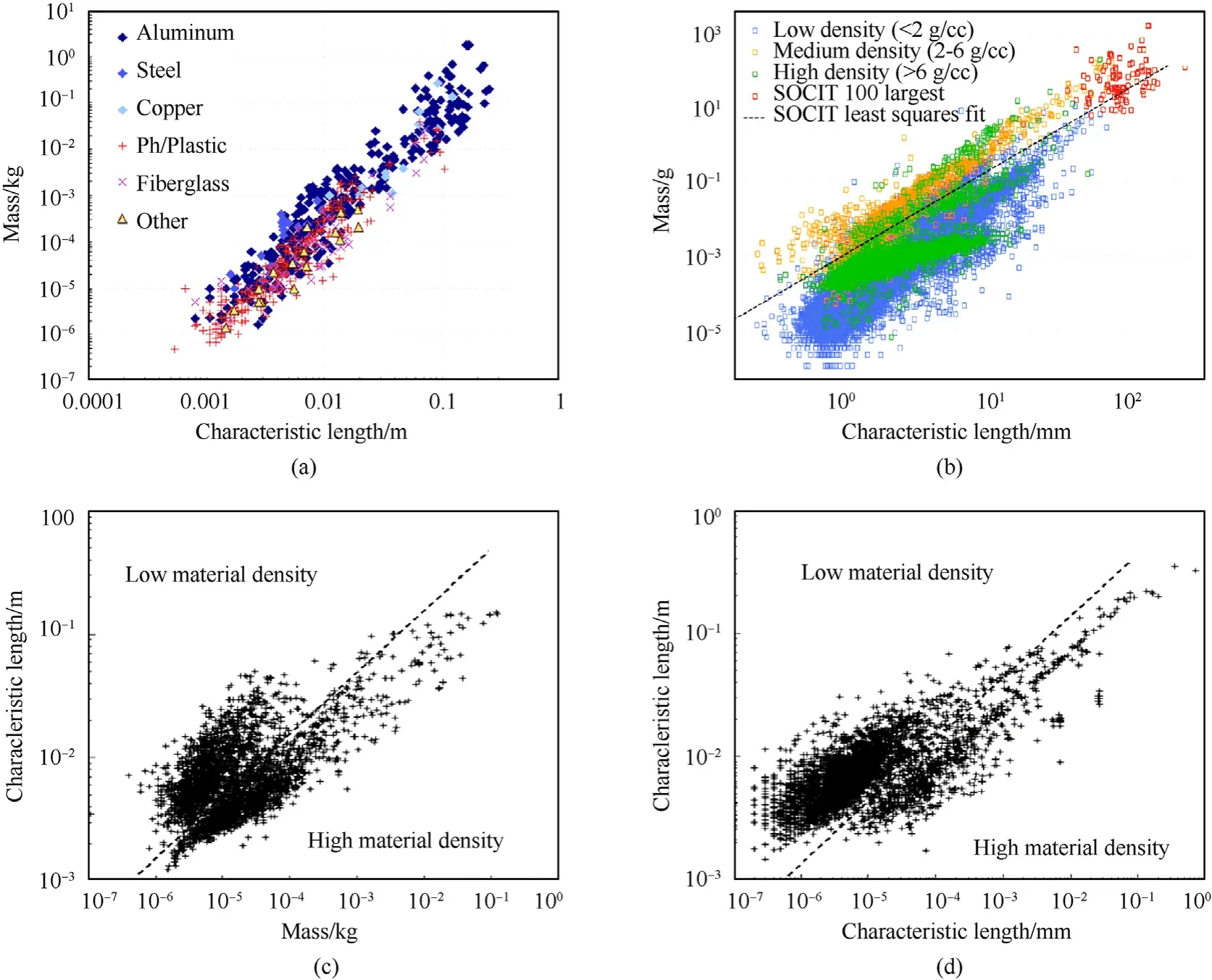
Fig.18.Mass/size relationship of breakup fragments obtained from different tests based ground: (a) SOCIT tests;(b) DebriSat tests;(c) CubeSat tests;(d) MicroSat tests[60,80,108,159].

Kessler given a conversion method between size and mass,however,the fragment was considered to be a sphere,and the diameter was used to represent the fragment size:

where,ρmax=4700 kg/m3,mc=2.60104× 10-4 kg,p=1.13.Previous NASA standard breakup model,the power relationship was used for a conversion method between size and mass

where,dcis the critical diameter of fragments,anddc=c1=0.01664,c2=0.26.According to the CubeSat experimental results,Hanada et al.[75,79] proposed a conversion between mass and characteristic lengthLcof breakup fragments:

The mass/size relationship was not described in a simple equation in the latest modified NASA standard breakup model.In order to convert a givenA/mto mass the average cross-sectional area,Ax,was modeled as having a one-to-one correspondence withLc,then the mass of breakup fragments can be calculated according to the equations ofAx/Lc.

4.2.1.2.Explosion.Bess the mass distribution of explosion was established based on the data analysis of thin walled cylindrical shell explosion in the literature [142].For hypervelocity projectile impact of a spacecraft wall,the number of fragments fits a power law.The number of fragments for both high-intensity and lowintensity explosion fits an exponential law.

where,N0and C are constants,N0and C values of high intensity explosion is higher than that of low intensity explosion.In FAST breakup model,McKnight [154] presented a mass distribution of explosion fragments according to the metal shell charge explosion tests,and the mass distribution form is an exponential law form similar to Eq.(30).WhereN0=1×10-4-1×10-3(nominal 5×10-4) andC=0.02-0.06 (nominal 0.04).In IMPACT breakup model [153],calculation method of coefficient was given,C=0.00102(Eexp/mt),mtis the total mass involved in explosion,Eexpis the energy released by explosion [137].

Kessler modified the mass distribution model by distinguishing the fragments according to the mass for explosion [143,144].

where,mtotis the total mass of the pre explosion object in grams,N01=1.71× 10-4,C1=0.02056,N02=8.69× 10-4,C2=0.05756.In the Battelle breakup model,the mass distribution of breakup fragments was proposed according to the explosion intensity.According to the explosion breakup observation data of SPOT-1 Ariane third stage [84-86],the exponential law was applied for lowintensity explosion,and the power law similar to that of impact debris was applied for high-intensity explosion.

Low-intensity explosion:

High-intensity explosion:

where,A=0.439,B=0.75,C=0.5,k=2.

In previous NASA standard breakup model,the mass was employed as the independent variable in developing functions for the number of fragments for explosion [105,160].Reynolds et al.[158]revised the number of fragments to an equation with size as a variable,and a single event may produce fragments that follow both distributions according to the Ariane upper stage sub-scale explosion tests supervised by the European Space Agency [95].The explosion size distribution has the form.

Low intensity explosion:

High intensity explosion:

where,A,B,andCare three positive constants,and that depend on the mass of the parent object.

The most obvious change in the latest NASA standard breakup model was the abandonment of the different size distribution based on low explosion intensity and high explosion intensity[44,160].Through the re-examination of Atlas tank explosion test results [165] and the observed data of cataloged fragments from numerous orbital breakup events,it was found that 10% of the fragments followed high-intensity explosion size distribution while the remaining 90% followed low intensity explosion size distribution.The production of explosive breakup fragments followed a simple power law [166].

To summary,the mass distribution function with mass as variable was first used to describe the fragment distribution.It is usually assumed that the fragment is spherical.The mass distribution mostly adopts power law and exponential law,and the application range of the function coefficient determined by experiment is usually small,which is due to the neglect of the influence of the fragment shape.The size distribution with the characteristic length as the variable can take into account the shape of irregular fragments and is closer to the real situation.

With analysis of data over the last decade,it is found that using the power law in the same form as impact can more effectively describe the mass and size distribution of explosive breakup fragments.The main difference between explosion and impact is the exponent of power law,which is determined by the scale energy.Because the impact energy is directly proportional to the square of velocity and often has higher energy than explosion,the input energy of impact breakup is higher,so it has a larger magnitude power law exponent.This fact leads to the low slope of mass distribution of explosive breakup fragment that were originally modeled with an exponential curve.Therefore,both impact breakup and explosion breakup generally adopt power law to describe the mass and size distribution in the latest disintegration model.

As shown in Table 6 and Table 7,For the power and exponential functions with mass as variable similar to Eq.(9) and Eq.(30),the value range ofAis 0.1-17,Bis 0.3-1.1,and N0is more obvious,which indicates that there are great differences in the fitting coefficient values of different experimental results,which is undoubtedly detrimental to the universality of the model.In the NASA standard breakup model,whether explosion or impact,distribution of breakup fragments can be represented by a simple power law with size as variable,and different S ormtotcan describe the breakup results under different conditions.This also provides an idea for us to improve the model in the future.The scaling factorScan be expressed by other factors related to projectile and target parameters,such as shape,density,and velocity,to establish a more generally suitable breakup model,so that a function can be used to describe the breakup results under various conditions.In addition,the size distribution is divided into explosion and impact,however,the breakup caused by the projectile impacting the satellite fuel tank is ignored,which is the combined effect of impact and explosion.It is necessary to establish a general satellite breakup model considering both impact and explosion.

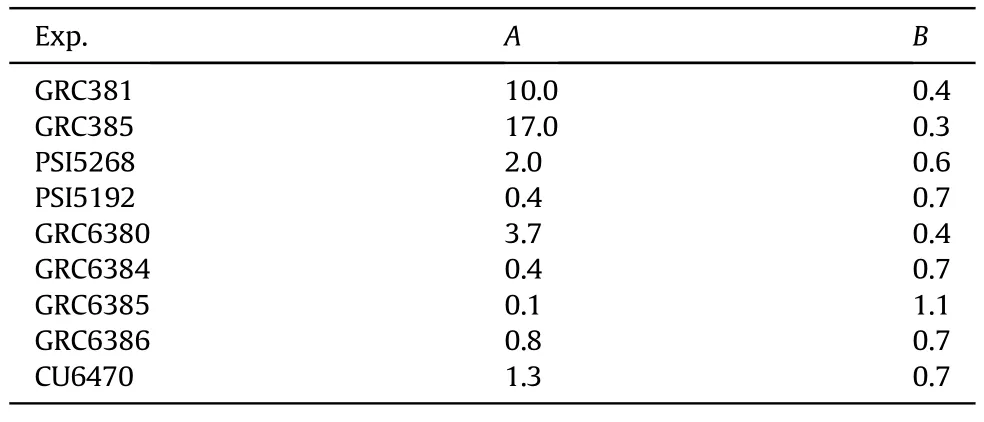
Table 6 The coefficient value of the mass distribution function like Eq.(9) [46,48].

Table 7 The coefficient value of the mass distribution function like Eq.(30) [140].

4.2.2.Area-to-mass ratio distribution

The A/M distribution determines the solar radiation pressure and atmospheric drag perturbations on the breakup fragments,which is directly related to the orbital lifetimes of fragments below about 1000 km altitude.For larger breakup fragments(larger than 10 cm),it can be tracked and identified by ground radar,and the size information of fragments can be inferred from RCS.However,due to the limitation of technology,it is difficult to obtain data for small breakup fragments,and even millimeter sized fragments will pose a serious threat to spacecraft.So,it is necessary to establishA/Mdistribution model to predict the orbital evolution of small fragments.

In the Battelle breakup model for MASTER debris environment model [146],the calculation method of the A/M of breakup fragments is as follows: firstly,convert the mass into the diameter of fragments according to the mass/size conversion Eq.(23),then calculate the cross-sectional area of fragments,and finally obtain the area-to-mass ratio of fragments according to the following equation [147]:

where,theAeffis the average cross-sectional area of fragment.In previous NASA breakup model [44],theA/Mwas a single-valued function related to fragment mass calculated by a similar method.According to hypervelocity impact tests,the modified NASA breakup model using normal distribution to describe theA/Mdistribution.Thus,for such objects,the calculatedA/Mis more effective for computing orbital lifetime in EVOLVE 4.0 than for determining the mass of the fragments through a relationship with size.TheA/Mdistribution function for upper stage fragments withLclarger than 11 cm is given by a bi-normal distribution of [160].

TheA/Mdistribution function for spacecraft large fragments withLclarger than 11 cm is similar toA/Mdistribution function for upper stage fragments,and only the parameters of small particles are different:

For small objects withLcsmaller than 8 cm,a single A/M distribution function has derived from hypervelocity impact experiments as follows:

where,

Since the NASA standard breakup model was established based on SOCIT test results using old satellites,the observation data of breakup fragments of Cosmos 2251,an older satellite,are welldescribed by the A/M distribution of NASA standard satellite breakup model [167],as shown in Fig.19(a).However,for the modern satellite Iridium 33 [108],there are noticeable discrepancies between the model predictions and the observation data,as shown in Fig.19(b).

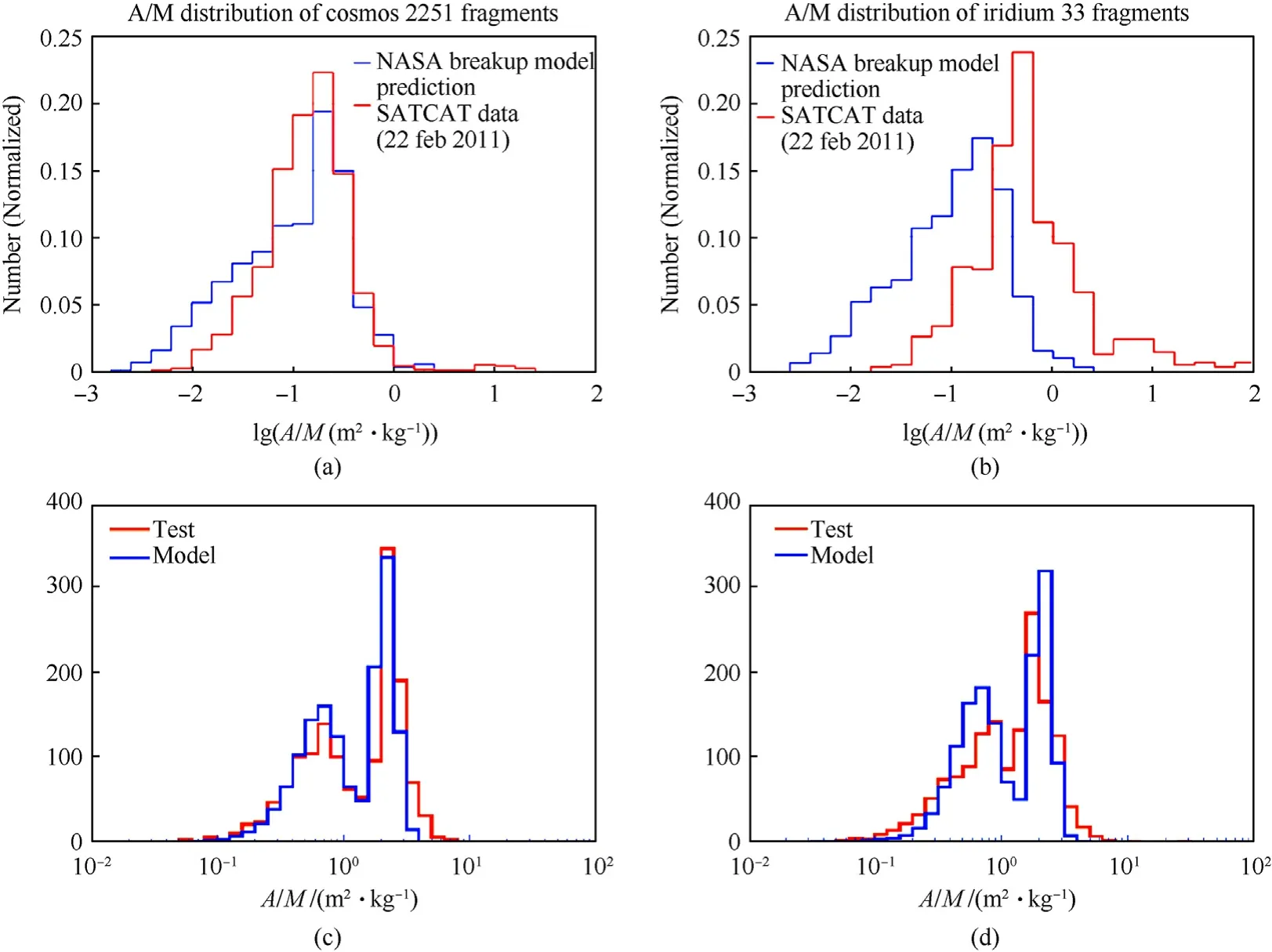
Fig.19.Comparison between A/M distribution and test results: (a) Comparison of NASA standard breakup model A/M distribution and Cosmos 2251 satellite fragments;(b)Comparison of NASA standard breakup model A/M distribution and Iridium 33 satellite fragments;(c)Comparison of NASA standard breakup model A/M distribution modified by Hanada et al.and CubeSate-HVI tests fragments;(d) Comparison of NASA standard breakup model A/M distribution modified by Hanada et al.and CubeSate-LVI tests fragments[69,108].

Oswald [168] found that the mass/size relationship of submillimeter fragments obtained from the area mass ratio in NASA's disintegration model was inconsistent with the actual situation.According Battelle breakup model,by assuming that theA/Mof small fragments is equal to theA/Mof sphere,the relationship betweenA/Mmean and characteristic length was redefined to better reflect the sub-millimeter objects.The corrected model then uses the small fragments parameter set

Hanada [44] found from the results of small satellite impact tests that multiple material density groups can be distinguished in the size/mass relationship,which was the main reason for the two peaks ofA/Mdistribution.Therefore,theA/Mdistribution of small debris should also be described by a size-based material density binormal distribution[169],and the expression of parameter set was given.The newA/Mdistribution model for small fragments described very well the fragments observed in the micro-satellite impact tests,as shown in Fig.19(c) and (d),Fig.19 [108].The A/M distribution of small fragments is shown as follows:

CARDC breakup model used three normal distributions with linear relationship to describe the A/M distribution according CARDC hypervelocity impact tests[51,52,156],and the three normal distributions represented aluminum,circuit board and other three main materials respectively.

From the results of orbital breakup and ground impact tests,the normal distribution can be used to describe the A/M distribution well.A single normal distribution can describe satellites made of fewer materials,but it is not suitable for modern satellites made of multiple materials.Because size distribution of fragments from the modern satellite breakup is closely related to the material density,it is necessary to describe theA/Mdistribution by multiple normal distributions with linear relationship to describe multiple peaks.The mean value μ(λc) and standard deviation σ(λc) of normal distribution are functions with the characteristic length as the variable,and the expression of the function varies according to the value range of characteristic length.The method of verifying the accuracy of the μ(λc) and σ(λc) functions by comparing the mass/size relationship obtained by converting size to mass using A/M distribution with the experimental data is commendable.At present,the improvement is still to modify the function of mean and deviation in order to better conform to the experimental and observed data in a larger size range.

4.2.3.Delta velocity distribution

Delta velocity determines the density and expansion velocity of fragments cloud induced by breakup,and also affects the orbital life of fragments.In the Battelle breakup model,the delta velocity was expressed as a function of fragment diameter,as shown below[148,149]:

In the previous FAST model,each fragment size was assigned a delta velocity,and the delta velocity was given by

Brown modified Eq.(57)into a hyperbola function with mass as variable by replacing mass with size,which means that each fragment mass was given a velocity [170].

Mcknight presented a delta velocity function with fragment diameter as variable similar to Eq.(56)

In NASA [160] standard breakup model,a normal distribution with A/M as the variable was used to describe the delta velocity distribution

where,χ=lg10(A/M),v=lg10(Δv),impact and explosion breakup have different parameters.

Explosion:

Oswald [168] modified the NSA standard breakup model to adapt to the increase rather than decrease of velocity distribution caused by high A/M of small-size fragments.The improved parameters can be calculated as follows:

Explosion：

As shown in Fig.20,the experimental data show that the delta velocities of breakup fragments decrease with the increase of size,and the decreasing trend increases.Battelle breakup model can better describe the delta velocity distribution of small size fragments,while the calculation results of large size fragments are significantly different from the test results.The velocity distribution of the uncorrected NASA standard breakup model does not change significantly with the fragment size,and the velocities assigned to small fragments are still significantly below the Battelle model.The velocity distribution obtained from the corrected NASA standard breakup model is assigned more delta velocity to small fragments,which is closer to the real situation.

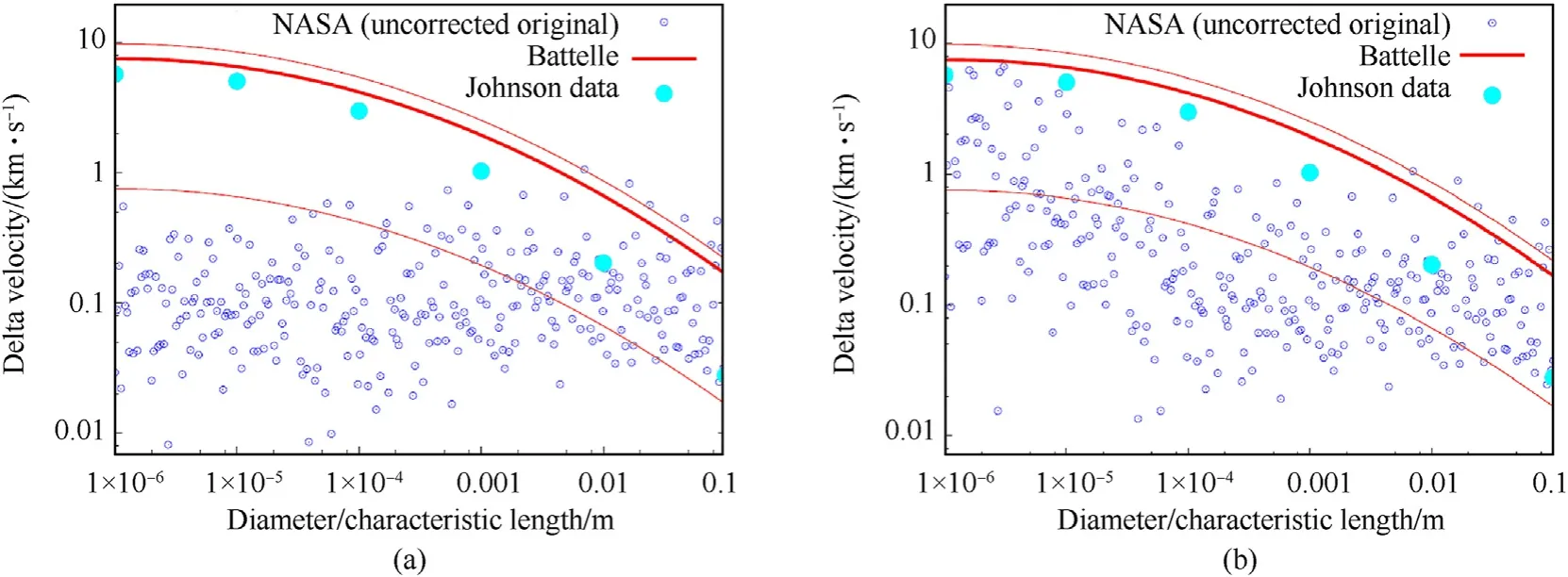
Fig.20.Comparison of velocity distribution between uncorrected,corrected NASA standard breakup model and Battelle breakup model: (a) Velocity distribution of uncorrected NASA standard breakup model and Battelle breakup model;(b) Velocity distribution of corrected NASA standard breakup model and Battelle breakup model [168].

As shown in Table 8,Most breakup models used mass as the variable,while only NASA standard breakup model used size as the variable.However,when calculating the A/M distribution,it is still necessary to convert the mass into the characteristic size,and using the characteristic size calculated by the definition algorithm as the variable,it is more intuitive and easy to measure.Except for the CARDC model,the size and mass distribution generally used power law and exponential law,and the influence of impact conditions on the disintegration results was not considered.From the current experimental results,it is obvious that the shape and density of the projectile will have an important impact on the breakup threshold,size and number of fragments,which needs to be considered in further study.The spherical assumption of A/M distribution had been replaced by multiple normal distributions with linear relationship,which can better describe multiple peaks of A/M distribution caused by obvious differences in material density,but density was not introduced as a variable in A/M distribution.The results of a large number of in orbit and ground experiments show that the normal distribution can better describe the velocity distribution of breakup fragments.However,the impact conditions were not also considered,and the velocity direction distribution was not given,which is very important for the subsequent calculation of debris orbital evolution.

5.Summary and suggestion

The research on satellite breakup under hypervelocity impact and explosion is of great significance in the field of space debris environment modeling,spacecraft impact risk prediction,ASAT weapon design and damage effect evaluation.This paper summarizes and analyzes the research on satellite breakup behaviors and model,including orbital and ground-based tests,numerical simulation and theoretical modeling.

For the ground-based tests,it is still necessary to develop the hypervelocity velocity launch capability of larger mass projectiles to solve the problem of using scaled satellites target for tests.In addition,more researches are still concerned about the results of fragments after breakup,while ignoring the influence of the projectile shape,material and impact position on the results,as well as the mechanism affecting the results.A large number of experimental studies have been carried out on hypervelocity impact breakup,including the impact on real satellites.However,there are few explosion breakup tests on real satellite targets,and explosion breakup tests are mostly simulated by cylindrical shell explosion.At present,the studies on the breakup of micro-satellites with complex structures and diverse components are increasing,and results can provide a basis for understanding the influence of large-scale constellation satellite breakup on the space environment.Furthermore,in order to maintain the orbit and prolong the life in orbit,the satellite in orbit usually carries a large amount of fuel,and the possible result is that the combined effect of impact and explosion led to the satellite breakup.Therefore,it is necessary to conduct impact tests on satellite targets carrying fuel to study the distribution results of breakup fragments under the coupling effect of impact and explosion.

The results caused by a flake projectile and long rod projectile with the same mass impacting the satellites at hypervelocity are obviously different.Due to the huge difference in the ratio of kinetic energy to contact area,the flake projectile will shatter completely,and the fragments can impact the internal structure of the satellite.However,the long rod projectile is likely to penetrate the satellite,because the penetrating projectile still has high kinetic energy rather than transferred to the satellite.The influence of projectile shape,density and other parameters on the breakup results is noteworthy.

The most commonly method used in satellite breakup numerical simulation is the combination of finite element and particle methods,which uses particles to replace the failed elements due to fracture and phase transformation.However,it depends on the definition of material failure and phase transition to distinguish particles and finite elements.In particular,the size of small fragments represented by particles needs to be determined by clarifying the boundary of failed particles.In addition,it is necessary to adopt appropriate and more accurate parameters of equation of state and constitutive model to simulate the material phase transition in the impact and explosion process,which is essential for energy exchange,so as to improve the accuracy of numerical simulation.

Some specific suggestions are put forward for the ground-based test and numerical simulation of satellite breakup:

(a) The breakup results under a more range of impact conditions can be obtained,including mass,size,velocity,and shape,so as to provide a data basis for establishing a wide range of breakup model.

(b) It is necessary to carry out explosion breakup tests on satellite targets close to real satellite structures and materials to obtain the fragment distribution characteristics of explosive breakup.The solution of this problem depends on the development of hypervelocity launch technology of larger mass projectile to meet the needs of breakup tests for larger satellite targets.

(c) Conducting impact tests on satellite targets carrying fuel to study the distribution results of breakup fragments under the coupling effect of impact and explosion.

(d) Studying the breakup energy density threshold under different impact conditions including projectile velocity,material and shape,and establishing a function containing impact conditions as variables to describe the breakup threshold.

(e) Developing the numerical simulation of new materials,establish accurate parameters for equation of state and constitutive model,solve the phase transformation behavior of new materials including fiber materials,circuit boards and battery materials under impact and explosion,and provide the breakup data of satellite composed of new materials.

(f) Studying the failure mechanism of satellite structure under hypervelocity impact by numerical simulation and groundbased test,reveal the failure mode of connections and internal components caused by shock wave and debris cloud.

Currently,the breakup model usually includes mass and size distribution,A/M distribution and delta velocity distribution.For the mass and size distribution in the breakup model,cumulative number is often used as the function of mass or size,which is often described by power law and exponential law according to the breakup reason: collision or explosion.The parameters in most functions are the constants to be determined fitted according to the experimental results,which has no physical significance.However,impact conditions(velocity,mass,shape)and explosion conditions(propellant mass,energy density) can significantly affect the distribution of breakup fragments.From the experimental results,it is difficult for the distribution results of breakup fragments under different impact conditions to be accurately reflected by a breakup model,which leads to multiple modifications to the model.Therefore,the parameters representing these conditions should be used as variables of the function,so that a generally applicable breakup model can be established.The current research results show that the optimal description method of A/M distribution is to adopt the multiple normal distributions with linear relationship,because fragments with different densities have different A/M distributions.Therefore,taking the material density as the variable of A/M distribution is one of the solutions,instead of determining the number of normal distribution according to the material density of the satellite.In addition,similar to the previous reasons,modern satellite breakup is not caused by a single impact or explosion,but by the combined effect of the two,because modern satellites carry a large amount of fuel.It is necessary to establish a model to describe the satellite breakup results under the combined effect of impact and explosion.

Suggestions for further study of the breakup model are given as follows:

(a) Establishing a generally applicable size distribution by taking the impact condition as the variable.Taking the power law as the function,the relationship between the coefficient and the impact condition need be established.

(b) Taking the material density as the variable of A/M distribution,instead of determining the number of normal distribution according to the material density of the satellite.It is possible to take density as a variable of A/M distribution function.

(c) Establishing a breakup model to describe the breakup results of modern large long-time orbiting satellites under the combined effect of impact and explosion.This requires taking the energy released by the explosion into account the impact energy,and studying how chemical energy and kinetic energy affect the break results.

(d) Develop the trace back ability of the breakup model,which can be used to judge whether the satellite has been deliberately attacked and the type of intruder.It is necessary to establish a function that takes the breakup results as variables,and calculate the distribution range of impact conditions including projectile and target parameters.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgment

This work was supported by National Defense Science and Technology Program (A14007) and China National Space Administration Preliminary Research Project (KJSP2020020101,KJSP2020010304).