Natural vibration of cantilever porous twisted plate with variable thickness in different directions

Y.X.Ho ,Y.Y.Liu ,W.Zhng ,L.T.Liu ,K.C.Sun ,S.W.Yng

a College of Mechanical Engineering,Beijing Information Science and Technology University,Beijing,100192,PR China

b College of Mechanical Engineering,Beijing University of Technology,Beijing,100124,PR China

Keywords:Porous cantilever twisted plate Variable thickness Natural vibration Frequency veering Mode exchange

ABSTRACT In this paper,the blade is assumed to be a rotating variable thickness cantilever twisted plate structure,and the natural vibrations of variable thickness cantilever twisted plate made of metal porous material are studied.It is assumed that the thickness of the plate changes along spanwise direction and chordwise direction,respectively,and it changes in both directions.The classical thin shell theory,the first and second fundamental forms of surface and von Karman geometric relationship are employed to derive the total potential energy and kinetic energy of the cantilever twisted plate,in which the centrifugal force potential due to high rotational speed is included.Then,according to the Rayleigh-Ritz procedure and applying the polynomial functions which satisfy the cantilever boundary conditions,the dynamic system expressed by equations of motion is reduced to an eigenvalue problem.By numerical simulation,the frequency curves and the mode shapes of the twisted plate can be obtained to reveal the internal connection between natural vibration and the parameters.A series of comparison studies are performed to verify the accuracy of the present formulation and calculations,in which compared data come from experimental,finite element method and theoretical calculation,respectively.The influence of pre-twist angle,three different forms of thickness taper ratio and rotational speed on natural vibration,mode exchange and frequency veering phenomenon of the system is discussed in detail.In addition,the approach proposed here can efficiently extract analytical expressions of mode functions for rotating variable thickness cantilever twisted plate structures.

1.Introduction

Aero-engine plays a vital role in all kinds of military aircraft which is the main technical equipment of the aviation force.As a very important part of aero-engine,blade can promote the efficient work of the engine,which is a structure applied to transform airflow energy into kinetic energy.The high-speed rotation of the blade will make it be affected by centrifugal force,and the blade will also be subjected to aerodynamic loads,thermal stress,tip airflow,harmonic excitations and so on,which may cause large vibrations,thus affecting the reliability,safety performance and service life of the whole machine.Therefore,it is very important to research the dynamic responses and vibration characteristics of blades.

Over the years,scholars have conducted deep researches on the dynamic behavior of blades,and blades have usually been reduced to beams,plates and shells in researches,respectively.Assuming blades as rotating thin-walled cantilever beams,Yao et al.[1,2]investigated the nonlinear dynamic responses of them at various rotating speeds.Saravia et al.[3]used finite element method(FEM)to research the dynamic instability and natural vibrations of rotating composite beams.Librescu et al.[4]researched the natural vibrations of a functionally graded rotating cantilever beam in a high-temperature field.Liu and Ren [5] assumed the wind turbine blades as thin-walled closed-section beams made of anisotropic composite,and studied the dynamic characteristics of it.

Using geometric non-linearity theory,Ramamurti and Kielb[6]analyzed the natural frequency of twisted rotating cantilever plates.Rostami et al.[7] considered the effect of Coriolis,and computed the mode shape and natural frequency of rotating cantilever plates.Sinha and Turner [8] utilized the thin shell theory to derive the equation of motion of a rotating twisted cantilever plate under the centrifugal force field,and solved the natural frequency of it.Dokainish and Rawtani[9]considered the effect of presetting angle,and obtained the vibration properties of the rotating cantilever plate employing the FEM.Cao et al.[10] studied the vibrations of the sandwich cantilever plate with surface coating using the Chebyshev-Ritz method.Sun et al.[11] employed the Hamilton principle to analyze the free vibrations of rotating blades at arbitrary rotation speeds and stagger angles.Taking the functionally graded sandwich blade into account,Liu et al.[12]investigated the free vibrations of it.Gu et al.[13]analyzed the dynamic instability of cantilever rotating twisted plate with the geometric imperfection.

Kee and Kim [14] assumed the blade to be a cylindrical shell with moderate thickness,and found the vibration characteristics of the system by the finite element method.Zhang[15]researched the vibration frequency and modal shape of composite laminated cylindrical shells by using a wave propagation method.Simplifying the blade to twisted cylindrical shells,Hu and Tsuiji [16] and Sun et al.[17]studied the free vibrations,Niu et al.[18]researched the vibration behavior of graphene reinforced cylindrical shells with the aid of Chebyshev-Ritz method,Yao et al.[19] presented the nonlinear dynamics of torsional shells,Sofiyev [20] dealt with the free vibrations of laminated orthotropic conical shells using the FSDT.Liew et al.[21]studied the effect of initial twist angle on the free vibrations of cantilever flat conical shells and proposed a structural vibration model.

On the other hand,in order to reduce the loss caused by airflow passing through the blade tip,many scholars began to study the blade with variable cross-section structure.Varying thickness is one of the ways to change the cross-section of the structures.By changing thickness,the vibration performance can be improved,the centrifugal stress is also reduced,the weight of them is adjustable.Bazoune et al.[22]studied the free vibration modals of the tapered Timoshenko beam installed around the rotating rigid hub at a certain angle to the rotating plane,and discretized the beam elements using a finite element method.Na and Librescu[23]proposed a cantilever conical beam model with chordal and spanwise thickness changing simultaneously,and studied its dynamic characteristics.The Rayleigh-Ritz method was used by Oh and Yoo [24] to solve the natural frequencies of functionally gradient beams with variable thickness,and studied the influence of different geometric parameters on them.Kou et al.[25] carried out the dynamic response characteristics of rotating large deformation cantilever plate whose thickness changes simultaneously along the span and chord direction.Nguyen et al.[26]presented the research on nonlinear dynamics of continuous thickness change of sandwich composite plate in thermal environment and on elastic foundation.Kumari [27] studied the vibration characteristics of composite laminates with variable thickness under the assumption that the blade thickness changed along the span and chord directions.Ansari et al.[28] investigated the mode shape and vibration frequency of variable thickness rotating functionally graded blade at any installation angle.With the benefit of the FSDT for laminated plate,Kumar et al.[29]obtained the vibration properties of functionally graded porous cantilever plates with variable thickness.Li and Hao [30] established the dynamic model of twisted blade with variable thickness,and analyzed its natural frequencies and modes.Jie et al.[31] researched the nonlinear dynamics of the twisted conical shell with variable thickness rotating cantilever with the help of Galerkin method.Hu et al.[32]treated the blade as a conical cantilever twisted shell with gradually decreasing thickness only along the span direction,and studied its vibration characteristics.Zhang et al.[33] carried out the free vibration analysis on a graphene-enhanced rotating twisted cylindrical shell with variable thickness.

Recently,a growing number of scholars have begun to research the application of new materials in blades,such as carbon fiber,functional gradient materials and graphene et al.Porous materials have the value of replacing traditional single metal materials due to their excellent physical properties and stronger adaptabilities.For example,porous materials have the characteristics of heat absorption and high specific strength because of their inner pore characteristics,which can meet harsh working conditions and significantly improve the performance and life of the equipment.The application of porous material to aero-engine blades is of very important significance to improve the safety performance of engines.Tran et al.[34] studied the functionally graded (FG) porous varying thickness plate,and gave numerical calculations of free vibration and static bending.More research on functionally graded porous plates can be found.Among of them,Zhou et al.[35]analyzed the sound radiation and free vibrations of it,Cong et al.[36] studied its thermomechanical buckling and post-buckling responses,Rezaei and Saidi [37] calculated its free vibration with different boundaries,Safaei et al.[38] studied its thermoelastic behavior,and Wang and Zu [39] studied its large-scale vibration properties.In addition,Nguyen[40]studied the nonlinear dynamic and static responses of it.The problems that how the vibration properties of various porous plates and shells are influenced by porosity were studied by Heshmati et al.[41],Demirhan and Taskin[42]and Trinh et al.[43].Zhao et al.[44]considered different elastic boundary conditions,and analyzed the free vibration characteristics of plate.Sinusoidal shear deformation theory is another theory considering the transverse shear influence.On this basis,Wang and Wu [45] presented the free vibration analysis of FG porous cylindrical shells under different boundary conditions.By means of generalized differential quadrature method,Setoodeh et al.[46]studied the vibrational behavior of functionally graded porous hyperbolic shells under kinds of boundary conditions.Belica and Magnucki [47] improved the Bubnov-Galerkin method to research the stability of the porous cylindrical shell under simply supported boundary and combined loads conditions.Using a multiscale method,Gao et al.[48]studied nonlinear main resonances of the FG porous cylindrical shell.Applying the meshless approach to carbon nanotube/Poly plates,Wang et al.[49,50] studied its nonlinear vibration.Esmaeilzadeh and Kadkhodayan[51]and Golzari and Jafari[52] researched dynamic responses and vibroacoustic behavior of porous plate and truncated conical shells,respectively.

It is important to investigate the variable thickness twisted plate made of porous material.In this paper,the blade is assumed to be a rotating variable thickness cantilever twisted plate structure,and the natural vibrations of variable thickness cantilever twisted plate made of metal porous material are studied.It is assumed that the thickness of the plate changes along spanwise direction and chordwise direction,respectively,and it changes in both directions.The classical thin shell theory,the first and second fundamental forms of surface and von Karman geometric relationship are employed to derive the total potential energy and kinetic energy of the cantilever twisted plate,in which the centrifugal force potential due to high rotational speed is included.Then,according to the Rayleigh-Ritz procedure and applying the polynomial functions which satisfy the cantilever boundary conditions,the dynamic system expressed by equations of motion is reduced to an eigenvalue problem.By numerical simulation,the frequency curves and the mode shapes of the twisted plate can be obtained to reveal the internal connection between natural vibration and the parameters.A series of comparison studies are performed to verify the accuracy of the present formulation and calculations,in which compared data come from experimental,finite element method and theoretical calculation,respectively.The influence of pre-twist angle,three different forms of thickness taper ratio and rotational speed on natural vibration,mode exchange and frequency veering phenomenon of the system is discussed in detail.

2.Theoretical formulation

Consider a variable thickness cantilever metal porous twisted plate which is shown in Fig.1.

Fig.1.Model of variable thickness cantilever twisted plate.

Cartesian coordinates systemOXYZis fixed on the center of rotating hub,andO1X1Y1Z1is got by translatingOXYZ.xaxis is in the spanwise direction whiley1axis is in the chord direction of twisted plate.They-axis is a dynamic coordinate axis which is used to describe the torsion angle θ′(x)of the twisting plate at arbitrary point.Thezaxis andz1axis are perpendicular to the plane ofO1xyandO1xy1,respectively.Assuming that the pre-twist angle of the twisted plate at the opposite end of the clamped side is θ.Then,for the twisted plate with lengthLinxaxis,the torsion rate of isq=θ/L.Thus,the pre-twist angle at arbitrary point can be calculated by θ′(x)=qx.In coordinate systemO1x1y1z1,a position vectorr0in mid-plane of the twisted plate is represented by(see Ref.[15])

where(i,j,k)denotes basis vectors of coordinate systemO1x1y1z1.The Lame coefficients are computed by

The basis vectors of coordinate systemO1xyzare expressed in terms of Lame coefficients and (i,j,k) as

Then,the curvature and torsion of twisted plate in mid-plane are given by

where coefficients of the second basic formula can be written as

Three different types of variable thickness cantilever porous twisted plate are depicted in Fig.2.In Fig.2(a),the thickness changes linearly in the spanwise direction,while the thickness in the chordwise direction remains unchanged.Fig.2(b) exhibits the thickness of the twisted plate only varying linearly in theydirection.Fig.2(c) exhibits its changing linearly both in thexdirection and theydirection simultaneously.

Fig.2.Types of variable thickness:(a)Type 1(thickness changing in spanwise direction);(b)Type 2(thickness changing in chordwise direction);(c)Type 3(thickness changing in spanwise and chordwise directions).

Suppose the thickness at arbitrary point of variable thickness plates be given by Ref.[27].

Type 1：

whereh0is the maximum thickness at one edge of the plate,α denotes the thickness taper ratio along thexaxis,while β is the thickness taper ratio along theyaxis.

2.1.Materials of porous twisted plates

In this study,the porosity distribution in thickness direction is denoted by uniform distribution.Thus,the relationship between shear modulus,mass density and elastic modulus with thickness can be defined by follows [53].

where the porosity coefficient of the mass densityNmand pore rate coefficientN0are defined as

where ρ1and ρ2are maximun and minimum values of mass density,whileE1andE2are maximum and minimum values of Young’s modulus,respectively.The relationships between the coefficients inN0andNmare expressed by

Thus,the mass density and Young’s modulus of the twisted plate can be alternatively obtained by

2.2.Energies of the twisted plate

The displacements are determined by

The strains of the twisted plate in relation to above displacement field are given by

The constitutive relation of the system is obtained as

where material parametersQ11,Q12andQ66are defined as

The strain energy of the system is

Substituting Eq.(12)-(16) into Eq.(17),the strain energy is rewritten as

where

The centrifugal forceFcfor the unit volume of the rotating twisted plate may be obtained by

where Ω is rotational speed of the twisted plate.Potential energy caused by centrifugal force is given by Liu et al.[54]

where

and

where Θ=qL+φ.Thus,the total potential energy of the system is

One can easily see that kinetic energy of the rotational twisted plate includes two parts.One is caused by deformation of the plate and the other is caused by the rotation speed.The total kinetic energies can be calculated by

whereVgis defined as

2.3.Natural vibrations solution procedure

For natural vibration,the periodic solutions are supposed to be

where ω is natural frequency of the system,U,VandWare admissible displacement functions in three directions,respectively,which are given by algebraic polynomial satisfying cantilever boundary conditions,therefore we have (27) and (28) into Eqs.(24) and (25),definingLmax=Tmax-Umaxand applying the Rayleigh-Ritz procedure lead to

Eq.(29)can be alternatively simplified as an eigenvalue problem as

whereKrepresents the stiffness matrix,Mrepresents the mass matrix,respectively.The vectorX=[UijVklWmn]T.Due to the fact thatX=0 suggests only a trivial solution,Eq.(26) should satisfy

The natural frequency of the system can be calculated by solving the eigenvalues of the coefficient matrix.

3.Comparison studies

Comparison studies are carried out to validate the present formulation and numerical simulation.

Comparison 1:Consider an isotropic rectangular cantilever plate with variable thickness function (h(x,y)=h0(1 -αx/L))along the x direction,andL/b=2,L/h0=100 andh0=1.0,respectively.Material constantsE=1×106N/m2,μ=0.3 and ρ=1×103kg/m3are selected.The first comparison results are listed in Table 1 for the first five dimensionless frequencies (ϖ=from present and reference data[27,55],in whichD0is the bending stiffness and can be expressed asD0=Eh03/12(1 -μ2).It can be observed that when the thickness taper ratio α along thexdirection takes a value from 0 to 1.0,the first five orders natural frequencies are in good agreement with each other.Furthermore,the first six dimensionless frequencies for the plate with another set of geometrics are also compared with experimental results [57],finite element method (FEM) results [27,57]and numerical results [55,56],respectively,as shown in Tables 1 and 2.

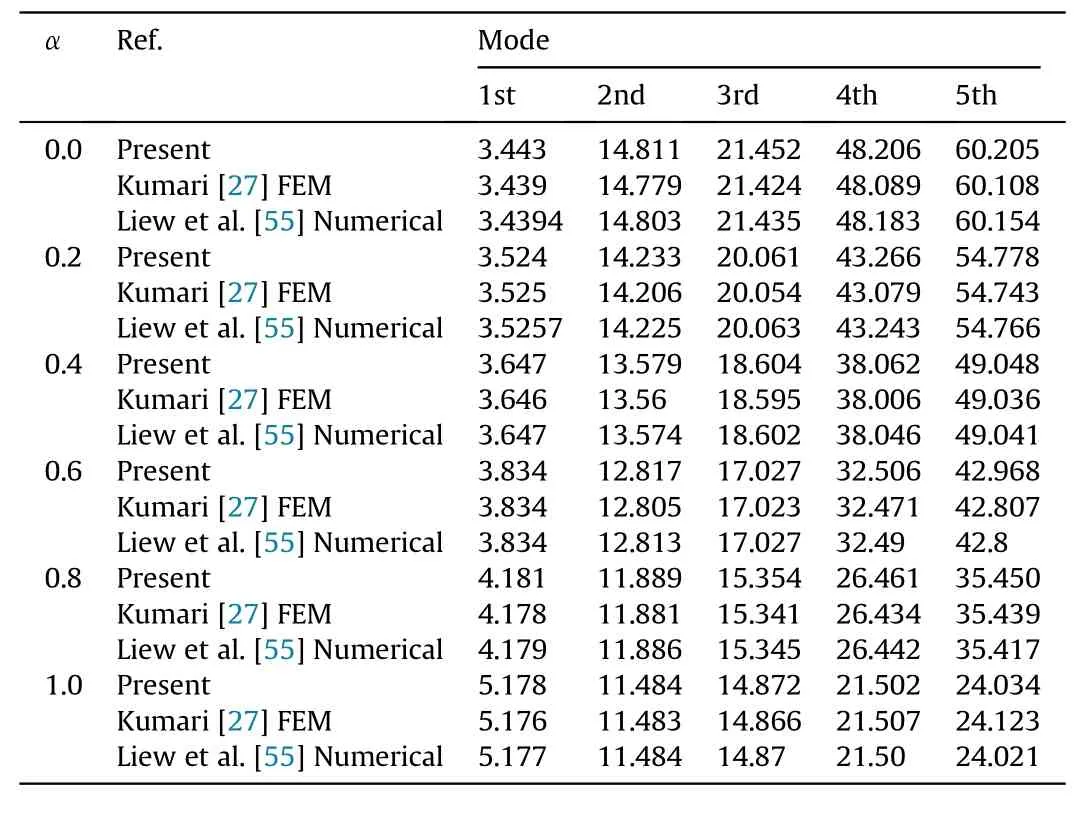
Table 1 Dimensionless frequency of an isotropic rectangular cantilever plate with variable thickness.

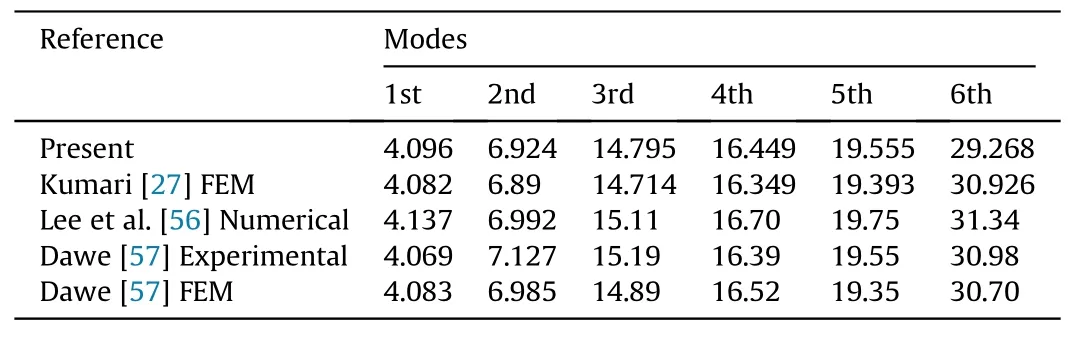
Table 2 Dimensionless frequency of an isotropic rectangular cantilever plate with variable thickness.

Comparison 2:Table 3 shows the first six dimensionless frequencies of an isotropic cantilever plate with (h(x,y)=h0(1 -β(0.5 +y/b))variable thickness along the y direction,and β=hmin/h0.The frequency results are taken as dimensionless ϖ=whereandhavg=(hmax+hmin)/2.The corresponding dimensionless frequencies arrived at from Kumari [27] and Lee [56] are also involved in this table for comparison.One can see that the frequency results in Table 3 are taken in good agreement with Kumari [27] and Lee[56].

Comparison 3:The values of the first five dimensionless frequencies of plates computed by the presented method and a discrete method by using Green function are tableted in Table 4.In this comparison,the plate whose thickness varies thexandydirections simultaneously (h(x,y)=h0(1 -αx/L)(1+β(0.5 +y/b)) is considered.The aspect ratios of it arerespectively.It is observed that the obtained results are in agreement with Huang[57]which the frequencies were obtained by numerical simulation,and the present method can achieve accurate solutions.

Comparison 4: In addition,the present results of mode shapes of variable thickness plate both inxandydirections are compared with those from Kumari[27].Fig.3 shows the first five mode shapes of the system with taper ratio α and β taking the same values as 0.5.It is found that present results agree well with the mode shapes of Kumari.It is worth noting that present results of frequencies and mode shapes are given by employing 7×7 terms foru,vandw.In other words,the first six frequency calculation by 7×7 terms for the three displacement components have enough accuracy to achieve the satisfactory convergent results.

Fig.3.Comparison of the obtained modes with Kumari [27] with (a) θ=0° and (b) θ=15° (L/b=4,b/h0=20,μ=0.3).

Comparison 5: Consider a rectangular cantilever torsion plate mounted on the wheel hub.The lengthL=88.6 mm,widthL=44.3 mm,thicknessh=3 mm,radius of wheel hubR=216.52 mm.Material constantsE=125 Gap,μ=0.3 and ρ=4370 kg/m3are selected.The plate has twisted angle β=5°and stagger angle β=30°.Calculate its natural frequencies at 0,5000 and 10,000 revolutions per-minute,respectively.The first three frequencies and mode shapes at the given rotational speeds are presented in Table 5,and the relative errors of frequencies are calculated.It can be observed that the first three frequencies and mode shapes at three rotational speeds are in good agreement with each other.

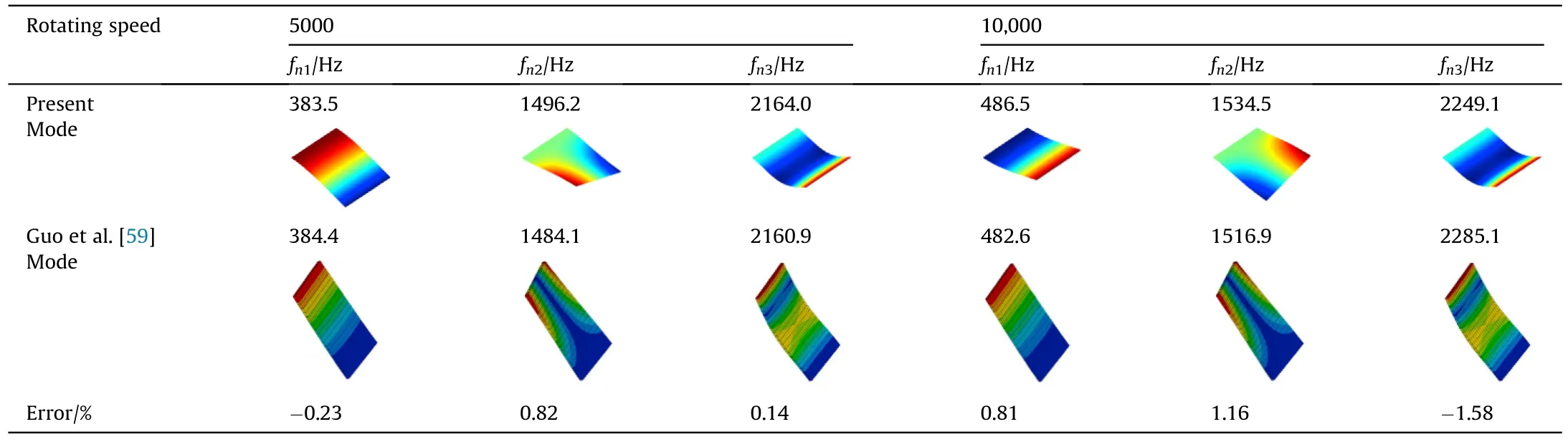
Table 5 Comparison of the first three frequencies and mode shapes with Guo et al.[59].

4.Natural vibration analysis

4.1.Static cantilever twisted plate

First,consider static state for the variable thickness metal porous cantilever twisted plate at 0°,15°and30°twist angles,respectively.A cantilever twisted plate (L/b=3/2,L/h0=100) is studied.The materials of porous aluminum with density ρ=2707 kg/m3,Young’s modulusE=70 Gpa,N0=0.4,Poisson ratio μ=0.3 are considered.Campbell diagrams are presented in Figs.4-6,where the thickness taper ratios of the variable thickness plate change from 0 to 1.0.

Fig.4 describes the effects of the thickness taper ratios on the first five nondimensionalized natural frequencies of the variable thickness plate with different types of thickness change mode.From Fig.4 for twist angle θ=0°,one can see that the natural frequencies above the first order decrease with increasing of thickness taper ratio.In addition,thickness taper ratio has little influence on the first natural frequency.The effect of thickness taper ratio becomes more obvious for the fourth order frequency and the fifth order frequency in which the rapid downward trend is found.It shows thickness taper ratio being more significant for high order frequency.It is worth mentioning that it is not necessarily universal.The effect of thickness taper ratio on the natural vibration is complex [29,60],and Fig.5 shows the variation of the first five principal mass and principal stiffness.Obviously,the increase of thickness taper ratio leads to a decrease of effective mass and stiffness for each order frequency at different rate of change.Moreover,with the increase of the thickness taper ratios,the region near the thin free edge of the cantilever twisted plate in vibrates more violently.It is because that these regions will more thinner and flexibility.

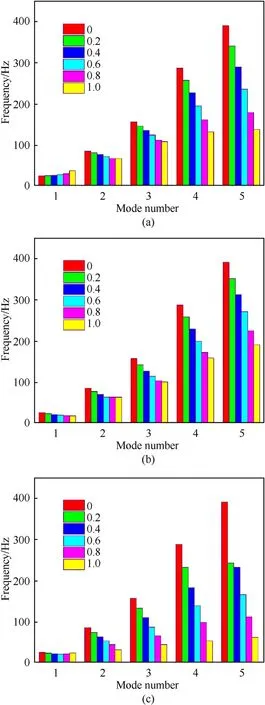
Fig.4.The first five frequencies of the system with thickness taper ratio at θ=0°:(a)Type 1(Variable thickness in x direction);(b)Type 2(Variable thickness in y direction);(c) Type 3 (Variable thickness in x and y directions).

Fig.5.The first five principal stiffness and principal mass of the system with thickness taper ratio at θ=0° and Type 3: (a) Principal stiffness;(b) Principal mass for.

Fig.6 contains curves of the first five nondimensionalized natural frequencies versus thickness taper ratio for twist plate (θ=15°).In this case,with the increase of thickness taper ratio the natural frequencies show different trends.Under Type-1 increasing thickness taper ratio of the plate only α,or under Type-2 increasing thickness taper ratio of the plate only,the first frequencies remain unchanged.The second-order frequencies decrease monotonically at a smaller rate with taper ratio increasing than the fourth-order and fifth-order frequencies.These two order frequencies decrease fast with the increasing of α or β,and then have a much lower decreasing rate at 0.8.

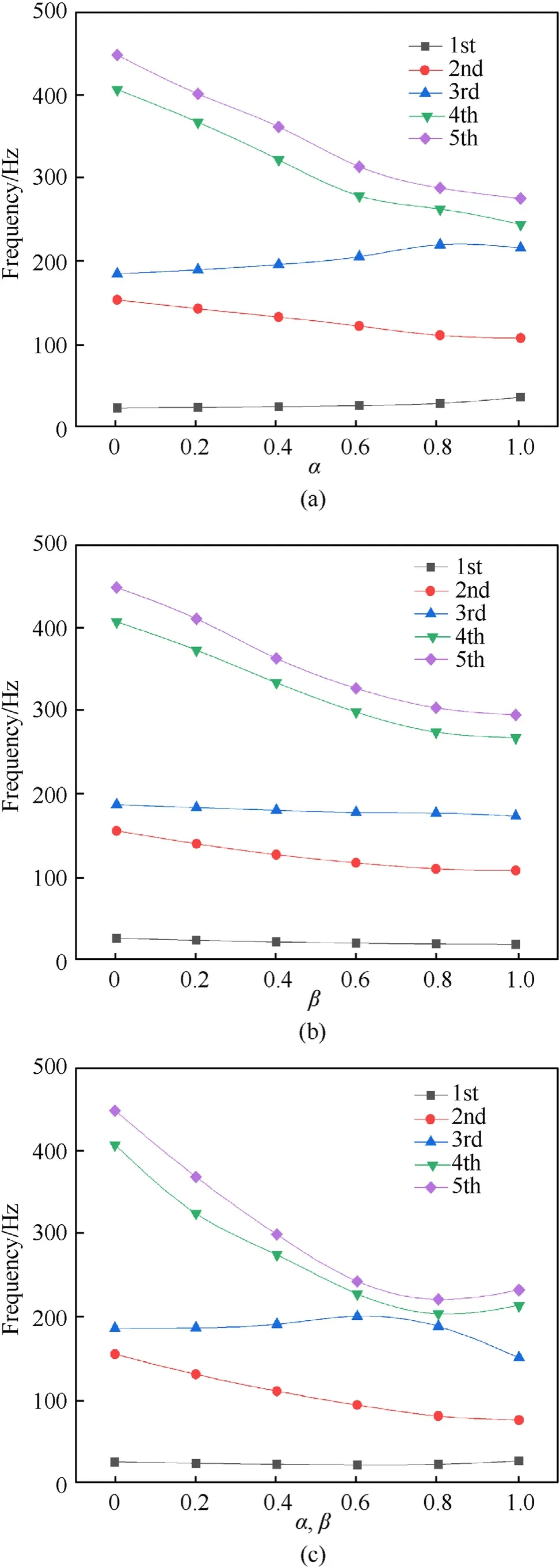
Fig.6.Variations of the first five frequencies with the taper ratio at θ=15°:(a)Type 1;(b)Type 2;(c) Type 3.

Comparatively speaking,for the case of Type-3 which both α and β change at the same time,the frequency change gets complicated.As the thickness taper ratio increases,the thirdorder frequency increases firstly and then decrease,while the fourth-order and fifth-order frequencies show opposite trends.Note that,the third-order and fourth-order frequencies coincide around α=β=0.7 and then separate,which imply a frequency veering between mode 3 and mode 4.It is because the third and fourth mode shapes of the system at α=0 and β=0 are the torsional mode and the second bending chord-wise bending.They are all deformed in chordwise which is more vulnerable to the thickness taper ratio because it is a short side.And at α=β=0.7,the torsional mode changes to spanwise bending mode,while the fourth mode shape changes to spanwise bending mode,as shown in Table 6.

Campbell diagram shown in Fig.7 describes the changes of the first five frequencies for three different types of variable thickness plates with thickness taper ratio θ=30°.In Fig.6(a),thickness taper ratio changes inxdirection only.It is obvious from Fig.7(a)that as the taper ratio increases,the first-order frequency increases,while the second-order frequency decreases slightly.There are two frequency veering,mode 3 and mode 4 exchange at α=0.4,mode 4 and mode 5 exchange at α=0.8.The influence of the thickness changes inydirection on the natural frequency of the system is researched for β from 0 to 1.0.As can be seen,the third-order frequency decreases more slowly than the fourthorder frequency,and the two frequency curves change direction at β=0.6,as plotted in Fig.7(b).Suppose the thickness of twist plate changes along two directions,Fig.7(c)describes the effect α and β on natural frequency for twist plate.From Fig.7(c),it is clear the third-order frequency carries maximum rate of decline after α=β=0.2.When α,β<0.2,the fourth-order frequency and the fifth-order frequency decrease more fleetly than other three frequencies.

Fig.7.Variations of the first five frequencies with the taper ratio at θ=30°: (a) Type 1;(b) Type 2;(c) Type 3.0°

By comparing these Figs.4,6 and 7,it found that the first two orders frequencies are not sensitive to pre-twist angle,which is thanks to the mode shapes are the first and second bending modes,while modes 3-5 are first order torsion mode,bending-torsion mode and second order torsion mode,respectively.It indicates that the torsional vibrations of the system vary dramatically when the pre-twist angle gets bigger.The mode shapes for porous variable thickness cantilever twisted plate with different twisted angles are shown in Fig.8.

Fig.8.Modes of metal porous cantilever twisted plate with different twisted angles under Type 1 (α=0.3).

4.2.Rotating cantilever twisted plate

Next,the analysis will be limited to rotating cantilever twisted plate.Fig.9 gives the first five natural frequencies for three types of rotating twisted plate which is defined by θ=0°,φ=0°andN0=0.4,respectively.The thickness tape ratios α and β have the same value of α=β=0.3.The stiffening of the twisted plate is affected owing to the centrifugal force.As described in Fig.9,in all cases,the frequency veering takes place between the 3rdorder and 4th-order frequency,and 4th-order and 5th-order frequency,but the frequency veering positions are different.Under the type 1,the 4th-order and 5th-order frequencies coincidence around 4000 rpm,and then the 4th-order and 3rdorder frequencies coincidence around 6000 rpm,as shown in Fig.9(a).At the same time,corresponding mode shapes exchange,specifically,the 1st-order bending-torsion coupling mode exchanges with the 2nd-order torsional mode interchange firstly,then it exchanges with the 2nd-order bending mode.Under type 2 and type 3,the frequency veering also occurs around 4000 rpm for 4th-order frequency and 5th-order frequency,the frequency veering also occurs around 6000 rpm for 3rd-order frequency and 4th-order frequency,respectively.Fig.9 indicates that the rotating speed has been caused great influence on mode 3 with nodal lines inydirection and mode 4 (the second torsion frequency).In Fig.10,mode 5 changes from two nodal lines in x direction to two torsion mode.

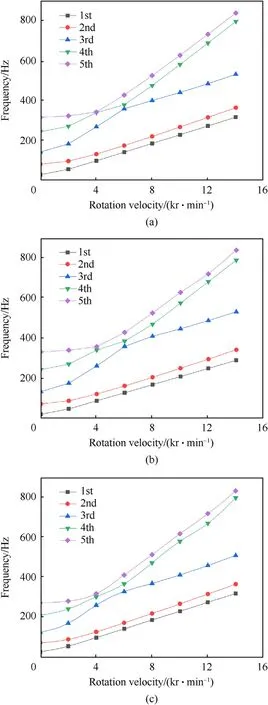
Fig.9.Variations of the first five frequencies with the rotation velocity with θ=0°:(a) Type 1;(b) Type 2;(c) Type 3.

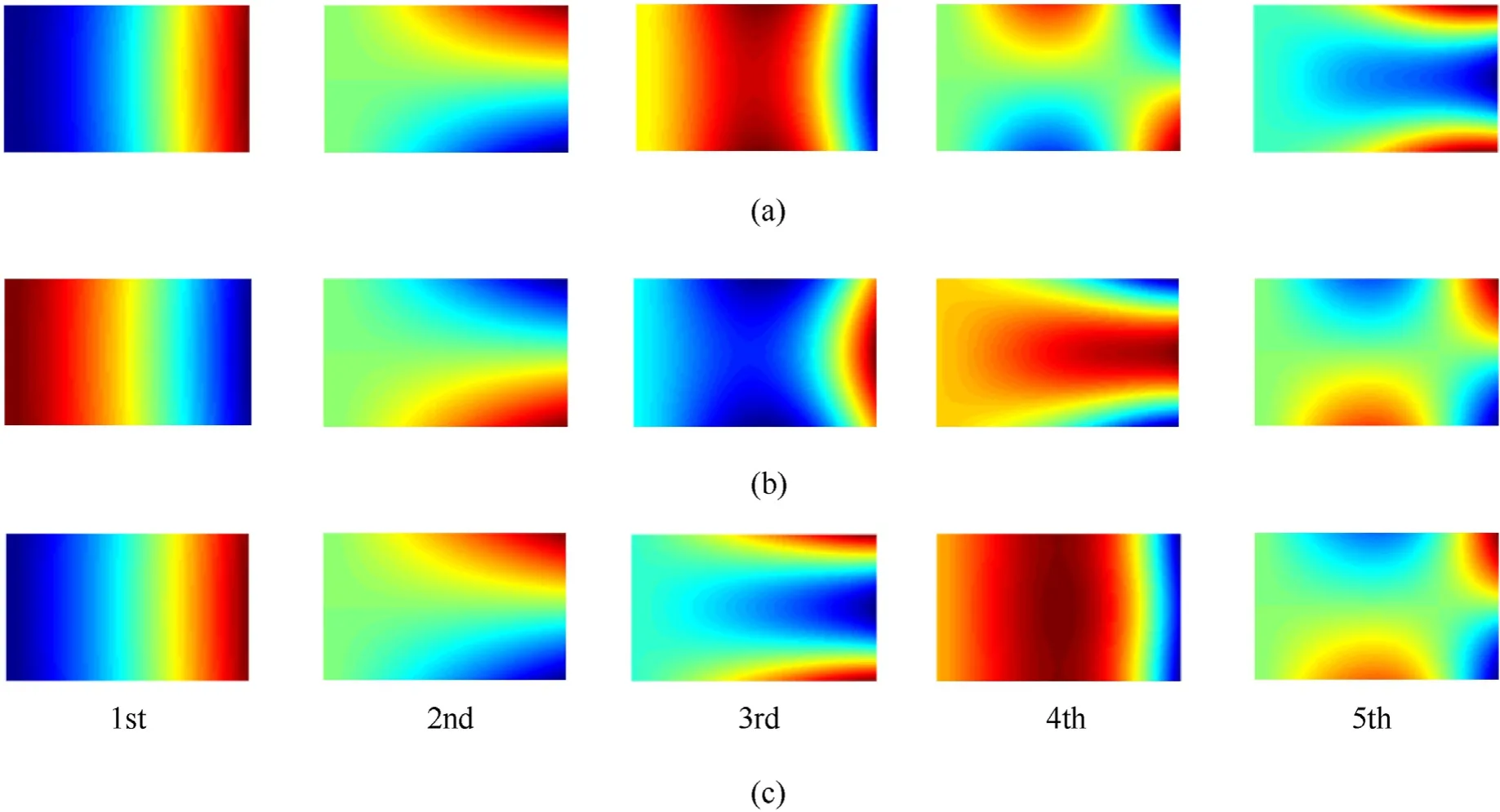
Fig.10.Modes of metal porous cantilever twisted plate with variable thickness under Type 1 when Ω=(a)2000,(b)5000,(c)12000 rpm (θ=0°).

The first 5-order natural frequencies with the change of rotating speed are plotted in Fig.11 for three types of variablethickness plates having pre-twist angle θ=15°,setting angle φ=45°.It is observed that for all cases,frequency curves rise with increasing of rotating speed.The growth slope of thirdorder frequency curves and the fourth-order frequency curves have appreciable variation compared with other frequency curves.Thus,in all cases,frequency veering occurs between the 2nd,3rd and 4th order frequencies,mode shapes of them exchange two times.For type-1,the first veering between the mode 2 and mode 3 take place at 2000 rpm,then frequency of the third-order and the fourth-order frequency is turned around in the vicinity of 8000 rpm.It is clear that the second-order bending mode is firstly exchanged with the first-order torsional mode,and then the second-order bending mode is exchanged with the bending-torsional coupling mode,as seen in Fig.12.Under Type 2,the frequency veering positions also appear around 2000 rpm and 8000 rpm,respectively.Under Type 3,the frequency steering position occurs around 4000 rpm and 6000 rpm.From Fig.12,one can see that the mode 3 and mode 4 is more sensitive to rotational speed,mode 3 with the first torsional mode changes to one with two transverse lines at 4000 rpm,and then has the mode shape with two nodal lines inxdirection.Thus,it can be seen that 8000 rpm is an important rotational speed for the cantilever plate with θ=15°.

Fig.11.Variations of the first five frequencies with the rotation velocity with θ=15°:(a) Type 1;(b) Type 2;(c) Type 3.

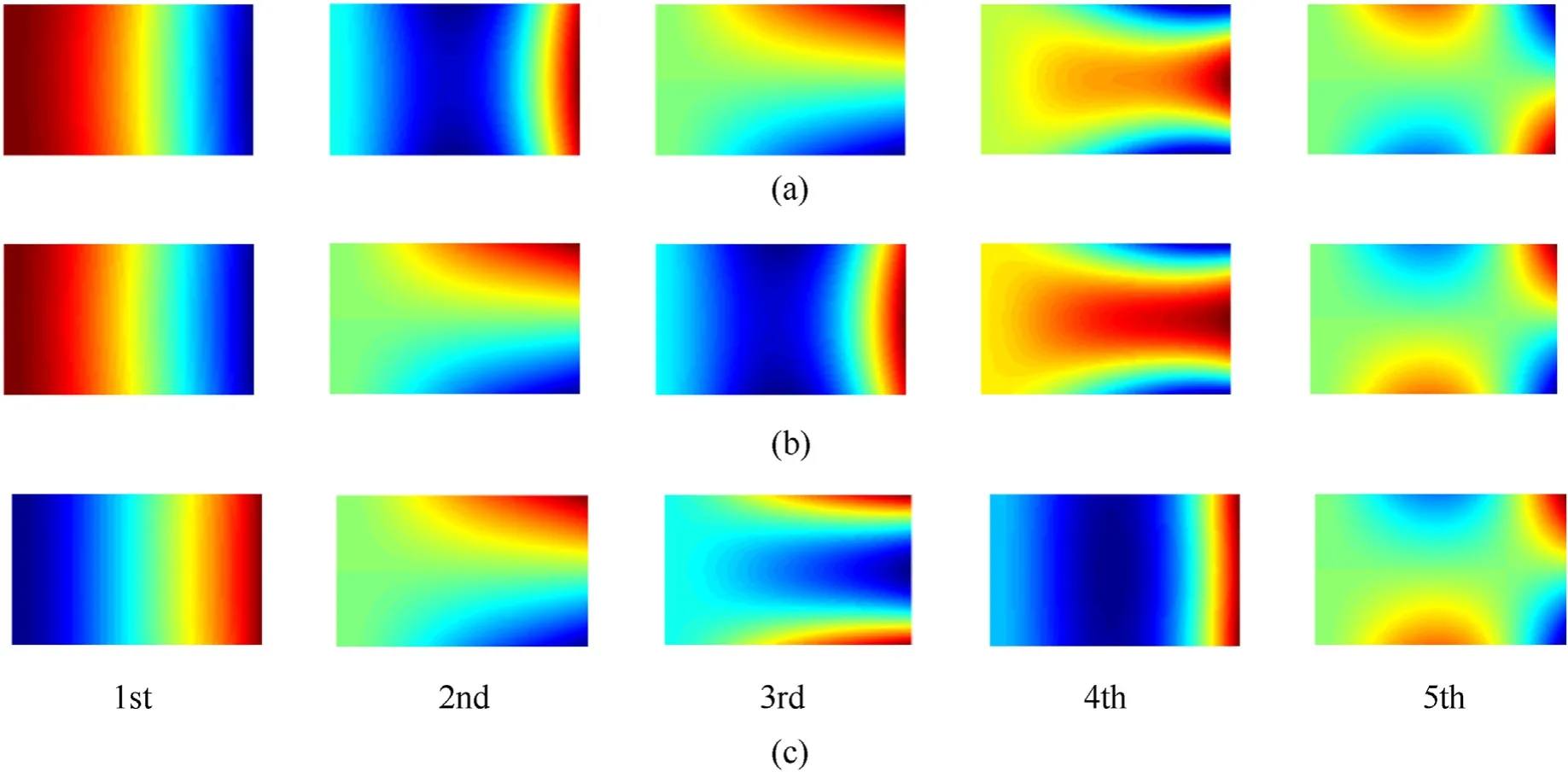
Fig.12.Modes of metal porous cantilever twisted plate with variable thickness: under Type 1 when Ω=(a)1000,(b)5000,(c)12000 rpm (θ=15°).

The frequency veering is further studied as twist angle increases to θ=30°.The Campbell diagrams of the first five frequencies with three types of variable thickness are drawn in Fig.13.In all cases,the first-order frequency increases with one slope only,while other four frequencies increase with various slopes in different regions.From Fig.13,it is observed that frequency veering appears between the second-order frequency and the third-order frequency at about 6000 rpm for all cases,and the third-order frequency and the fourth-order frequency around at about 10000 rpm for Type-1 and Type-2,respectively,while around 8000 rpm for Type-3.Thus,it can be deduced that 6000 rpm,8000 rpm and 10000 rpm are three important rotational speed for the cantilever plate with θ=30°.Fig.14 illustrates the vibration mode shapes of the Type-1 twisted plate with θ=30°.It is evident that all the first modes are the firstorder bending mode for all cases.In second bending modes,inplane vibration inxdirection can be seen.Furthermore,the second-order bending mode has been greatly affected by rotating speed.

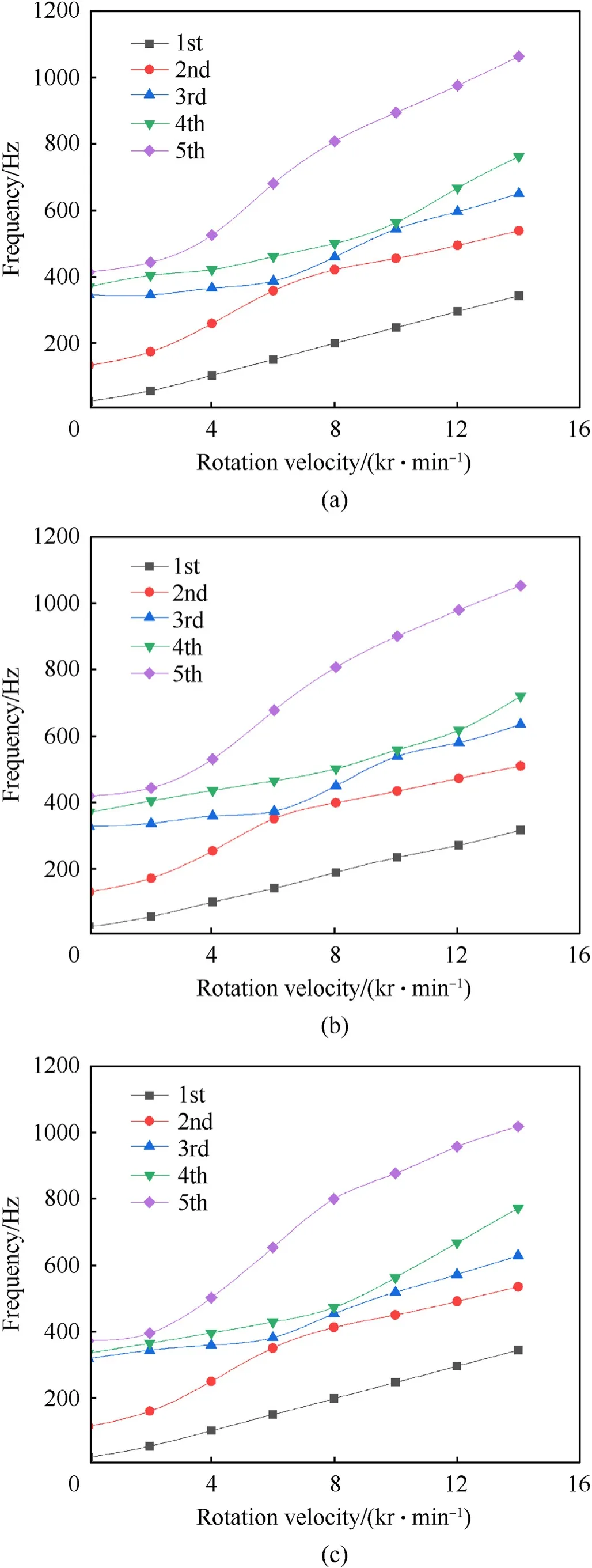
Fig.13.Variations of the first five frequencies with the rotation velocity with θ=30°:(a) Type 1;(b) Type 2;(c) Type 3.

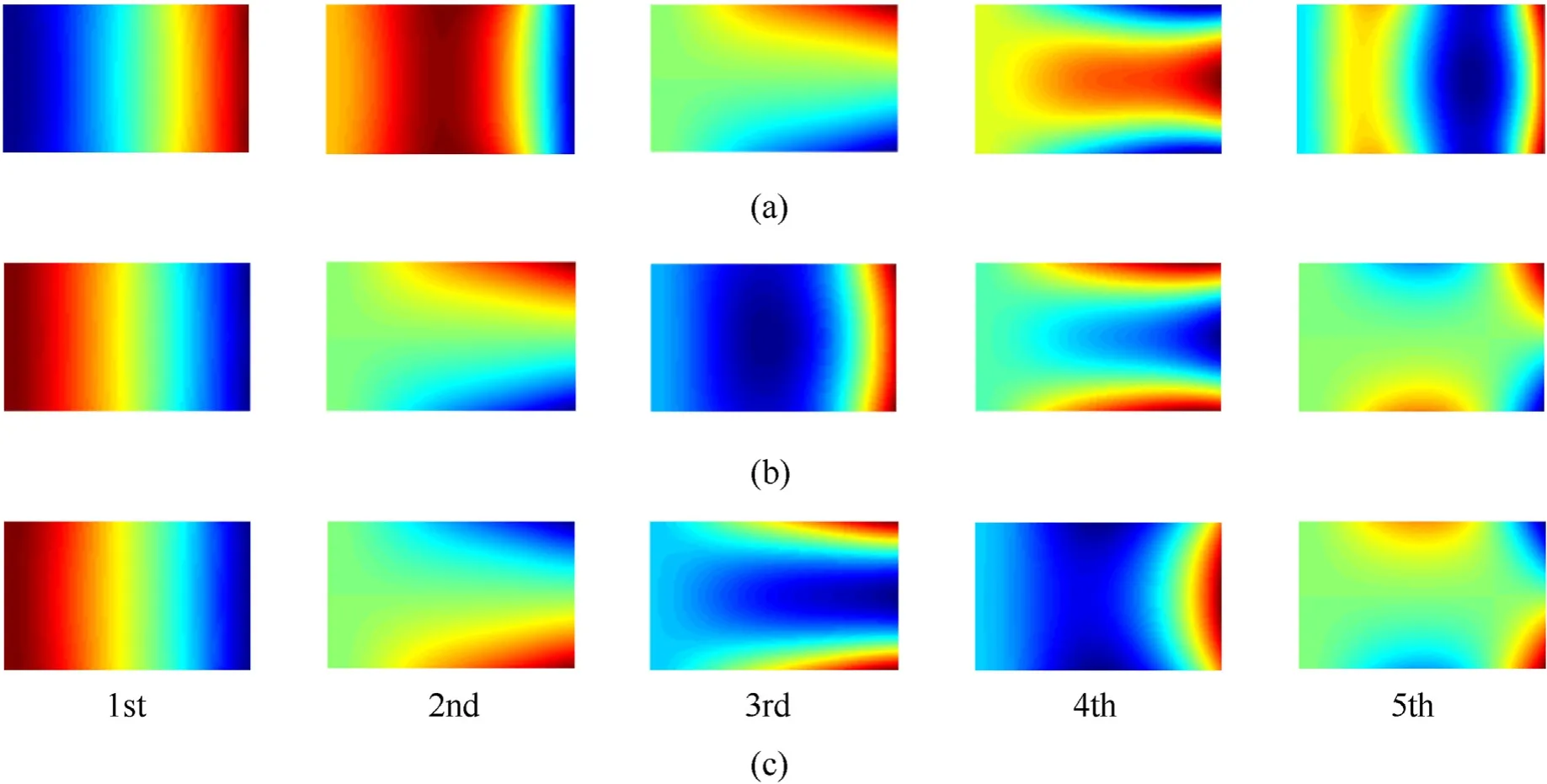
Fig.14.Modes of metal porous cantilever twisted plate with variable thickness under Type 1 when Ω=(a)6000,(b)9000,(c)12000 rpm (θ=30°).

Horizontal comparison of the three types of porous twisted plates shows that at the same rotational speed,the frequency of the porous torsion plate of type 1 is the largest,followed by the Type 2,and Type 3 in turn.Longitudinal comparison of the variation of the first 5-order frequencies with the rotational speed of the variable-thickness plates under three different torsion angles,it can be found that under different twist angles,the frequency veering arises between different frequencies around certain rotating speed.In the static state,the reason for the frequency veering is that the different thickness taper ratios have different effects on the natural frequencies and corresponding mode shapes.In the rotating state,it is mainly because the influence of the rotating speed on each order mode is different.However,it is known that the stiffness of the bending and the in-plane stretching increase with the increase of rotating speed,which leads to higher frequencies.Frequency veering is of great concern,because in this case internal resonance may be excited by the external excitation with the same frequency.

5.Conclusions

In this paper,the blade is assumed to be a rotating variable thickness cantilever twisted plate structure,and the natural vibrations of variable thickness cantilever twisted plate made of metal porous material are studied.It is assumed that the thickness of the plate changes along spanwise direction and chordwise direction,respectively,and it changes in both directions.The classical thin shell theory,the first and second fundamental forms of surface and von Karman geometric relationship are employed to derive the total potential energy and kinetic energy of the cantilever twisted plate,in which the centrifugal force potential due to high rotational speed is included.Then,according to the Rayleigh-Ritz procedure and applying the polynomial functions which satisfy the cantilever boundary conditions,the dynamic system expressed by equations of motion is reduced to an eigenvalue problem.By numerical simulation,the frequency curves and the mode shapes of the twisted plate can be obtained to reveal the internal connection between natural vibration and the parameters.A series of comparison studies are performed to verify the accuracy of the present formulation and calculations,in which compared data come from experimental,finite element method and theoretical calculation,respectively.The influence of pre-twist angle,three different forms of thickness taper ratio and rotational speed on natural vibration,mode exchange and frequency veering phenomenon of the system is discussed in detail.

The results show that torsion modes are more sensitive to pretwist angle.Thickness taper ratio has a greater impact on higher order frequency.It is worth mentioning that the effect of thickness taper ratio on the natural vibration is complex.The increase of thickness taper ratio leads to a decrease of effective mass and stiffness for each order frequency at different rate of change.

It's also found that with the increase of the thickness taper ratios,the region near the thin free edge of the cantilever twisted plate vibrates more violently.With the joint influence of both the thickness taper ratio and twisted angle,torsional vibration modes with higher frequencies are more vulnerable to influence.By the action of centrifugal force of rotational cantilever porous twisted plate,bending modes and corresponding frequencies deserve more attention.

In addition,the approach proposed here can efficiently extract analytical expressions of mode functions for rotating variable thickness cantilever twisted plate structures.In fact,mode functions obtained from the method developed can be used to establish the nonlinear ordinary differential equations of motion of the structure in a convenient,efficient and analytic way.In future study,multiple parameter optimization can be conducted for structure parameter of the blade in practical problem for a selected military aircraft.

Data availability statements

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors acknowledge the financial support of National Natural Science Foundation of China through grant nos.11872127,11832002,11732005,Qin Xin Talents Cultivation Program,Beijing Information Science &Technology University QXTCP A201901.