Numerical study on the dynamic fracture of explosively driven cylindrical shells

Zhi-yong Yin ,Xiao-wei Chen

a State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing,100081,China

b School of Mechatronical Engineering,Beijing Institute of Technology,Beijing,100081,China

c Advanced Research Institute of Multidisciplinary Sciences,Beijing Institute of Technology,Beijing,100081,China

Keywords:Metal cylindrical shell Shear failure Fragment distribution Numerical simulation Fragment velocity

ABSTRACT Research on the expansion and fracture of explosively driven metal shells has been a key issue in weapon development and structural protection.It is important to study and predict the failure mode,fracture mechanism,and fragment distribution characteristics of explosively driven metal shells.In this study,we used the finite element-smoothed particle hydrodynamics (FE-SPH) adaptive method and the fluid-structure interaction method to perform a three-dimensional numerical simulation of the expansion and fracture of a metal cylindrical shell.Our method combined the advantages of the FEM and SPH,avoiding system mass loss,energy loss,and element distortion;in addition,the proposed method had a good simulation effect on the interaction between detonation waves and the cylindrical shell.The simulated detonation wave propagation,shell damage morphology,and fragment velocity distribution were in good agreement with theoretical and experimental results.We divided the fragments into three regions based on their shape characteristics.We analyzed the failure mode and formation process of fragments in different regions.The numerical results reproduced the phenomenon in which cracks initiated from the inner surface and extended to the outer surface of the cylindrical shell along the 45° or 135° shear direction.In addition,fragments composed of elements are identified,and the mass and characteristic lengths of typical fragments at a stable time are provided.Furthermore,the mass and size distribution characteristics of the fragments were explored,and the variation in the fitting results of the classical distribution function under different explosion pressures was examined.Finally,based on mathematical derivation,the distribution formula of fragment velocity was improved.The improved formula provided higher accuracy and could be used to analyze any metal cylindrical shells with different length-to-diameter ratios.

1.Introduction

Dynamic fracture of axisymmetric metal cylindrical shells under internal explosive loading is a highly complex phenomenon.The failure of the cylindrical shell is affected by multiple factors,such as geometric shape,material properties,and loading characteristics,and there are multiple failure modes,such as tensile,shear,and hybrid fractures.The distributions of the velocity,mass,and size of the fragments are critical for the design of munitions and armaments.For decades,problems related to the expansion and fracture of metal cylindrical shells have attracted the attention of many researchers.

Gurney(1943)[1]proposed that the initial velocity of fragments of explosively driven metal shells could be expressed as a function of the charge-to-metal casing mass ratio,C/M.The Gurney formula is widely used due to its simplicity and accuracy.However,the Gurney formula is unsuitable for calculating the velocity distribution of the fragments of the cylindrical shell because the influence of the rarefaction waves from the ends of the warhead on the fragment velocities is not considered.Many experts have carried out further research on this basis[2-6],among whom Huang et al.[6] modified the formula proposed by Zulkoski [2];the obtained velocity distribution was in good agreement with the experiment.The foremost method used to obtain the fragment velocity distribution of an expanding cylindrical shell is to modify the Gurney formula combined with experimental data.However,the rationality of the corrected term and the applicability of the modified formula to cylindrical shells with different length-to-diameter ratios require further investigation.

Mott[7] was the first to analyze the statistical size distribution of fragments,and the proposed unloading wave model laid the foundation for this field.This theory assumes that material fracture is random.Shells break at certain points,generating waves on both sides of the fracture surface,and the unloaded area cannot initiate a new crack again.Therefore,the propagation distance of the release wave can be considered the fragment size.Grady and Kipp [8,9]established an energy-based theory of dynamic fragmentation based on Mott[7]that linked the strain rate of blast loading and the fragmentation scale;this theory is applicable to brittle materials[10].Zhou et al.[11],Lambert et al.[12],and Goloveshkin and Myagkov [13] established prediction models for fragment sizes based on different theories.However,most of these theoretical models are one-dimensional;when applied to actual threedimensional fracture problems,the prediction results of the fragment size are not accurate.

Many researchers recovered typical fragments through experiments and obtained their mass distribution,size distribution,and fracture characteristics by weighing and measuring them [14-18].Arnold and Rottenkolber [19] proposed a method for fast data collection for fragmenting shells based on image processing.All these studies promoted research on the mechanism of fragment size control.

The Taylor criterion was proposed to predict the failure strain of an expanding cylindrical shell [20].In this model,radial cracks initiate at the outer surface of the casing,where the hoop stress is tensile,and then propagate inward.When the stress at the inner surface is converted from a compressive to a tensile state,the crack penetrates the casing.Hoggatt and Recht [21] further developed Taylor’s work[20]and proposed that cylindrical metal shells could have different fracture modes under different detonation pressures.Hoop tensile fractures typically occur only when the detonation pressure is relatively low and characteristic shear-lip fractures appear,while the cylindrical shell deforms at a higher detonation pressure/-strain rate,confirmed in many subsequent experiments[22-26].Singh et al.[27] explored the fracture characteristics of aluminum and copper cylinders with different wall thicknesses under different loading strain rates,finding that the rupture strain increased with the strain rate for a fixed wall thickness.However,when the wall thickness was different,the rupture strain reached a maximum value at a certain strain rate.Liu et al.[28]analyzed the fracture behavior of a 1045 steel cylindrical shell subjected to internal explosive loading and performed a fine numerical simulation of the initiation and propagation of multiple shear bands.

As an axisymmetric structure,the failure position of the cylindrical shell is random.This spontaneous failure can reflect the probabilistic nature of fracture.Therefore,it is necessary to model the stochastic distribution of defects and inhomogeneities in the structure of the material,and explore the probabilistic nature of the initiation and development of cracks and the characteristic size of fragments [29,30].Fracture and fragmentation mechanisms form the core of the dynamic expansion of metal shells under internal explosive loading.At present,researchers provide explanations based on their respective experimental and numerical results;however,there are still some differences in the initiation and propagation of cracks,and more experiments and theoretical analyses are needed.

Similar to experimental research,numerical simulation plays an important role in the study of the expansion and fracture of explosively driven metal shells.Comparatively,through numerical simulation,we can obtain real-time information about the failure process,stress,strain,and temperature of the cylindrical shell;this information is of great importance for studying the different failure modes.Moreover,numerical simulations can be used to carry out single-variable research to verify existing theoretical models.Current simulation algorithms applied to explosively driven cylindrical shells are primarily based on the finite element method(FEM),such as the Lagrange algorithm [16],Euler algorithm [31,32],and Arbitrary Lagrangian-Eulerian (ALE) [33,34].However,the traditional FEM method simulates the fracture by removing the failed elements,causing an excessive loss of mass,momentum,and energy in the system,thus not reflective of the real physical phenomenon.Due to the large deformation of the cylindrical shell under explosive loading,the FEM method also causes element distortion.In recent years,many studies on meshless algorithms have been conducted,with smoothed particle hydrodynamics(SPH)being the most popular.Grisaro and Dancygier[35]used the fluid-structure interaction method and SPH method to study the velocity distribution of fragments caused by explosively driven metal shells and explored the influence of different failure criteria of the casing material on the velocity distribution.Kong et al.[36]used the SPH method to simulate and analyze the propagation of detonation waves,expansion and rupture processes,and the expansion velocity of a metal casing.However,meshless methods still have some defects,such as tensile instability and unclear material boundaries.Therefore,combining traditional FEM methods with meshless methods is a pioneering direction for current simulation research on the expansion and fracture of explosively driven metal shells.

In this study,the FE-SPH adaptive method and the fluid--structure interaction method were used to investigate the fragmentation of a cylindrical metal casing under internal explosive loading.In the simulation,the SPH particles are used to continue calculating instead of failed elements,thus combining the advantages of FEM and SPH.Subsequently,the numerical results were analyzed from several perspectives,such as the propagation of detonation waves and fracture modes of the cylindrical shell.In most experiments,the damage modes were analyzed by recovering the fragments,but the original positions of the recovered fragments in the metal shell could not be determined.This study extracted typical fragments at different positions along the axis of the cylindrical shell from the numerical results,analyzed their failure modes according to their morphology and loading condition,and provided the mass and characteristic length of the typical fragments.The mass and size distributions of the fragments under different explosion pressures were explored,and the applicability of the existing distribution functions was discussed.In addition,the distribution formula for the fragment velocity was improved to provide an alternate solution that can be used in engineering practices.

2.Numerical simulation method

2.1.FE-SPH adaptive method and fluid-structure interaction method

In the numerical study of explosively driven metal shells,the emphasis is on simulating the explosion and fracture of a cylindrical shell.The fluid-structure interaction method was adopted to simulate the explosion,i.e.,both the explosive charge and air were meshed by the ALE algorithm and then coupled with the shell divided into Lagrangian meshes.The metal shell expands and breaks outward through the pressure transmission between the explosive and inner surface of the casing.

The keyword CONSTRAINED_LAGRANGE_IN_SOLID can be used to implement the fluid-structure interaction method in the LSDYNA.The parameter CTYPE controls the coupling type,and CTYPE=5 indicates penalty coupling allowing erosion in the Lagrangian entities.This method avoids the distortion of elements,thus better describing the leakage of detonation products and the interaction between the detonation wave and the casing.

FEM and meshless methods are two commonly used methods for simulating casing materials.The FEM method describes fragmentation by removing the failed elements from the system,which will violate the laws of conservation of mass and energy.If there is a large deformation of the material,the elements may be extremely distorted and the solution may not converge.The meshless method uses numerous discrete particles to represent a continuum.When the distance between the particles is too large,the material is considered broken,effectively avoiding the above-mentioned defects.However,the meshless method also has some issues,such as tensile instability and unclear material boundaries;in addition,it cannot obtain information such as the distributions of mass,size,and energy of the fragments.

The FE-SPH adaptive method used in this study combines the FEM and SPH methods.Element distortion can be overcome by transforming the deleted elements into particles in the SPH.In addition,the SPH particle has the same mass,speed,material,and other parameters as the corresponding element,avoiding excessive loss of mass and energy.This method obtains the distribution of larger fragments composed of the remaining elements and tiny debris represented by SPH particles.

The keyword DEFINE_ADAPTIVE_SOLID_TO_SPH was used to implement the FE-SPH adaptive method.Referring to He et al.[37],the parameter ICPL=IOPT=1,indicates that the particles are activated and coupled with the elements after the elements fail.This setting can ensure high accuracy of contact between elements and can effectively avoid penetration between elements and particles.He et al.[37] used this method to simulate the debris cloud generated by hypervelocity impact and introduced the concepts of velocity and momentum space to describe risky fragments.The numerical results are consistent with the experimental results,and their work is of great significance for the study of the subsequent penetration process of debris clouds.

2.2.Simulation model

To study the fragmentation of explosively driven cylindrical metal shells,this study used the LS-DYNA software,based on the FE-SPH adaptive method and the fluid-structure interaction method,to reproduce the experiment of Feng et al.[38,39].This experiment investigated the fragment velocity distribution of an AISI1045 steel metal casing filled with Composition B under central point initiation.The experimental parameters are listed in Table 1,and the masses of the cylindrical shell and explosive were 154.31 g and 58.03 g,respectively.

Table 1 Parameters of numerical model.

Fig.1 shows the three-dimensional model established according to the parameters listed in Table 1.In the figure,the orange part is the metal cylindrical casing with open ends,the red part is the explosive charge,completely filled inside the cylindrical casing,and the blue part is the air area,set as the outer area of the explosive.The outer diameter of the air area is ΦD’=60 mm,and the length is L’=115.95 mm.Considering the scattering range of the fragments,such a setting can ensure that the fragments obtain sufficient acceleration in the air from the detonation products.For the adaptive method,the cylindrical casing is divided into 1,996,800 hexahedral Lagrange elements,with a minimum side length of approximately 0.18 mm.The explosive and air parts were divided into 5,574,000 hexahedral ALE elements and coupled with the cylindrical casing by the fluid-structure interaction method.The outside of the air part was set as a non-reflection boundary condition.

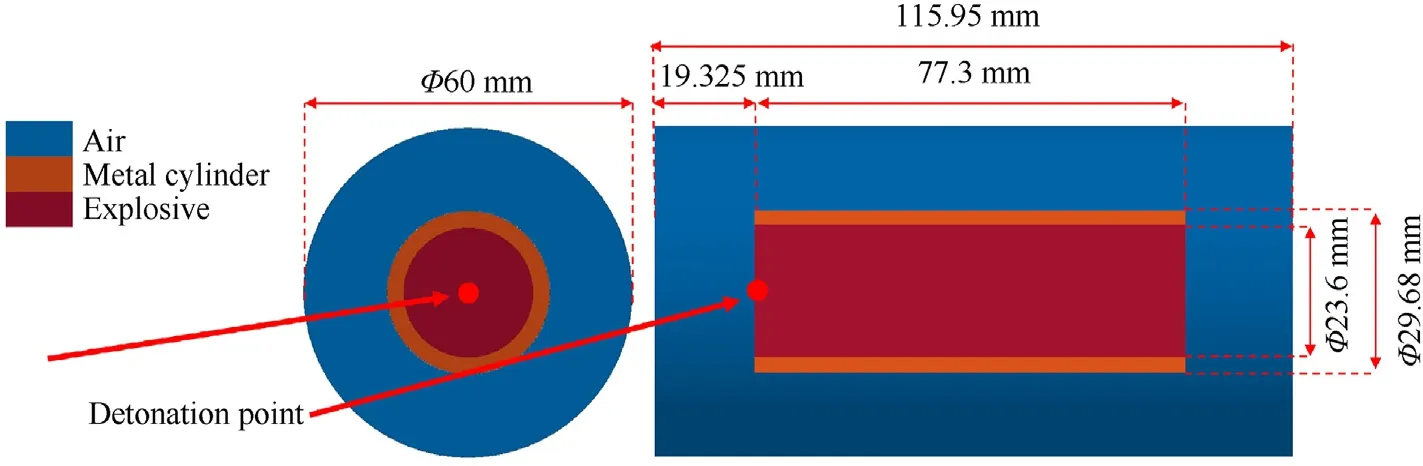
Fig.1.Calculation model.

2.3.Material models

In the present study,the Johnson-Cook(JC)strength model[40]and Gruneisen equation of state [41] were selected to model the material behavior of the AISI1045 steel cylindrical casing.The JC model is widely used to describe materials subjected to a high strain rate [42],expressed as

whereA,B,n,C,andmare constants of the material,ε is the equivalent plastic strain,is the dimensionless effective plastic strain rate,andT* is the dimensionless temperature.The failure criteria were chosen with the maximum principal strain failure criterion and the JC failure model.The JC failure model is a cumulative-damage fracture model[43],which defines the damage parameter as

where Δεpis the increment of equivalent plastic strain which occurs during an integration cycle,and εfis the equivalent strain to fracture under the current conditions.D=0 initially and whenD=1 the failure occurs.The strain at fracture is given by

whereD1,D2,D3,D4andD5are constants of the material;σ*=p/σeff,which is the ratio of pressure divided by effective stress.The material model parameters are listed in Table 2.Referring to the experience of Li et al.[39],an acceptable numerical result was obtained by setting the maximum principal strain failure criterion to 0.65.

Table 2 Material parameters of AISI1045 steel.

The Jones-Wilkins-Lee(JWL)equation of state was adopted as the material model of the Composition B charge,as follows:

whereA,B,R1,R2,and ω are the constants of the material,andeandVare the internal energy per initial volume and initial relative volume,respectively.The explosive parameters are listed in Table 3[44].

Table 3 JWL parameters of COMP-B.

The EOS_LINEAR_POLYNOMIAL multilinear equation of state is adopted as the material model of air,as follows:

where μ is the specific volume,C0-C6are the constants of the material,andEis the internal energy per initial volume.The material model parameters are listed in Table 4.

Table 4 LINEAR_POLYNOMIAL parameters of air.

3.Results and verification

3.1.Propagation of detonation wave

The explosion is initiated at the center point of one end;the pressure contours of the cylindrical casing and detonation products at different moments after detonation are shown in Fig.2.The detonation wavefront is approximately spherical and has a large curvature at the initial stage of detonation (t≤1.5 μs).As the detonation wave propagates,the curvature of the detonation wavefront decreases and gradually changes from a spherical wave to a plane wave;the oblique incidence angle of the detonation wave to the cylindrical casing gradually increases.The detonation wavefront is approximately perpendicular to the inner surface of the cylindrical casing att=6.5 μs,indicating that the explosion enters the sliding detonation stage at this moment.Fromt=2.5 μs tot=6.5 μs in Fig.2,when the detonation wave reaches the outer surface of the cylindrical casing,it is immediately reflected as a tensile wave,and then the internal stress state of the casing alternately changes between the tensile wave and the compression wave.Compared with the numerical results of Liu et al.[28],as shown in Fig.3,due to the different simulation conditions,the pressure distribution and maximum pressure are different,but the variation in pressure inside the shell is similar,changing alternately between tension and compression.The shape of the detonation wavefront is similar,and both develop into a stable plane wave.

Fig.2.Propagation of detonation wave.

3.2.Expansion and rupture process of cylindrical shell

The entire process of expansion and fracture of the cylindrical casing can be obtained through numerical simulation,intuitively reflecting the expansion and acceleration of the shell,initiation and propagation of the cracks,and the formation process and morphological characteristics of the fragments.Fig.4 shows the expansion and fracture morphology of the cylindrical casing at typical moments ranging from 0 μs to 30 μs.The red part represents the shell formed by the Lagrange elements,and the yellow part represents the newly generated particles.The explosion and air areas are hidden.Fig.5 shows the detailed morphologies of typical fragments att=70 μs,divided into three regions according to their failure modes and shape characteristics.

Fig.4.Time history of expansion and fracture of the cylindrical shell: (a) t=0 μs;(b) t=5 μs;(c) t=10 μs;(d) t=15 μs;(e) t=20 μs;(f) t=25 μs;(g) t=30 μs

Fromt=0 μs tot=10 μs in Fig.4,the shell was in the process of uniform expansion,and no noticeable cracks occurred at the outer surface of the casing.The elements at the head of the cylindrical shell(close to the initiation end)first reached the failure threshold,and a large number of upward splashing particles were formed under the action of the detonation wave.During the expansion of the cylindrical shell,fragments with different morphologies were formed because of the different forces at different positions of the shell.

The head of the cylindrical shell was subjected to dynamic strain in the circumferential and axial directions,with its deformation similar to the expansion of a spherical shell.This part separated from the cylindrical shell att=15 μs and formed an independent ring-like structure,as shown in Fig.4.With the continuous expansion of the ring,it finally separates into fragments in Region 1 of Fig.5.The size of the fragments in Region 1 was small,and the edges of the fragments turned outwards.Most fragments had the edge of the shell,and some fragments had incomplete cracks.

The middle part of the cylindrical shell was primarily subjected to circumferential strain.From Fig.4(d),when the head of the cylindrical shell breaks away,a large number of slender fragments are generated from the fracture,extending axially parallel to the metal shell.The crack spacing determines the width of the fragments.The large number of elongated fragments formed in Area 2 of Fig.5 is a usual feature of explosively driven cylindrical shells.Most fragments in this area were formed by shear fractures;the direction of the fracture was approximately 45°or 135°in the radial direction.Some fragments with large widths exhibited incomplete axial cracks in the middle.

The failure mode of the tail was similar to that of the shell head.First,the ring structure is separated from the shell,and then a large number of small fragments are generated with the fracture of the ring.Fig.4(d) shows that before the cracks are transmitted to the tail of the shell,the tail breaks under the detonation wave and rarefaction wave,and multiple thin rings are separated from it.Fig.4(e)-Fig.4(g)show that the velocity of the ring at the tail of the shell was higher than that at the head of the shell.These thin rings eventually fractured into fragments in Area 3 of Fig.5.Compared to Area 1,the fragments in this area were completely fractured and smaller in size.Only some of the fragments have shell edges,visibly turned outward.

Fig.5 presents the morphology and failure modes of the fragments and shows the mass and characteristic length of the four typical fragments-A,B,C,and D (Subsection 3.4 details the definition of characteristic length)-the basis for the subsequent analysis of the spatial distribution characteristics and damage effect of fragments.The mass and size distribution characteristics of the fragments are detailed below.

Fig.6 shows the top view of the failure process of the crosssection of the cylindrical shell after the SPH particles were hidden.Cracks initiated from the inner surface and extended to the outer surface of the cylindrical shell.Furthermore,Fig.7 shows the effective plastic strain of a certain fragment in the cross-section of Fig.6 during the formation process.

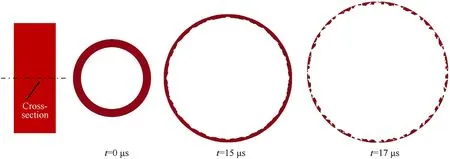
Fig.6.Failure process of the cross-section.

Fig.7.Detailed view of the fragment formation.

The expansion and failure of a cylindrical metal shell can be roughly divided into three processes.The first is the uniform expansion and deformation process.Beforet=13 μs,the inner surface of the cylindrical shell expanded uniformly under hoop tensile stress,with no clear damage occurrence.Att=15 μs,some elements at the inner surface of the cylindrical shell failed first,and the plastic strain no longer developed uniformly.Instead,strain localization occurred near the failed elements,which is the shear localization stage.The last stage is the crack propagation stage,during which an increasing number of elements in the shearlocalized zone fail,resulting in cracks.Subsequently,cracks developed rapidly along the shear localization zone to the outer surface of the shell at 45°or 135°,eventually penetrating the cylindrical shell.Due to the limitation of the calculation scale,the number of elements along the radial direction of the cylindrical shell is limited.Therefore,there is no clear shear zone in Fig.7,but the macroscopic fracture at approximately 45°or 135°is consistent with previous experimental and numerical results[27,28,45].From the theoretical analysis,the middle part of the cylindrical shell is subjected to circumferential strain,and the maximum shear stress surface is located in the direction of 45°or 135°with the radial angle,the key factor of the fracture mode.

Fig.8 shows the effective plastic strain histories of the different elements along the thickness direction of the cylindrical shell.The plastic strain of the inner surface element of the cylindrical shell is always at its maximum under the effect of detonation waves beforet=10.5 μs.The shock wave is reflected from the outer surface,producing an unloading wave that minimized the plastic strain on the outer surface element.The superposition of the reflected unloading wave and the loading wave makes the stress state in the middle of the cylindrical shell to alternate between tension and compression.The superimposed stress can cause a secondary plastic accumulation,which makes the plastic strain of the elements within 0.25 cm from the inner surface of the cylindrical shell relatively high but still smaller than that of the inner surface.Therefore,the elements at the inner surface failed first,and the subsequent damage propagated outward from the inner surface,consistent with the fragment formation process shown in Fig.7.

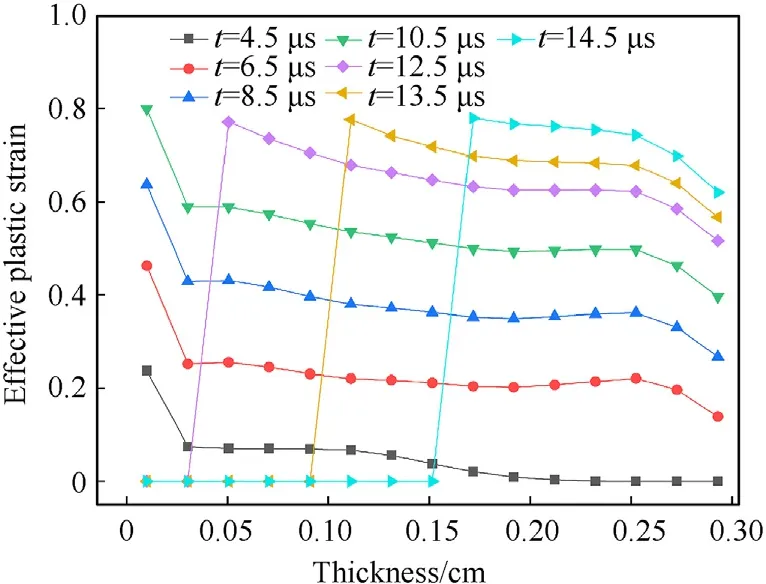
Fig.8.Effective plastic strain history at different radial locations.

The numerical results obtained in this study were compared with the experimental and numerical results of Li et al.[39],as shown in Fig.9.Li et al.[39] used AUTODYN software to simulate the fracture of a cylindrical shell based on the SPH method.The numerical results of the two methods for the slender fragments in the middle of the cylindrical shell were consistent with the experimental results.However,using the FE-SPH method,we can obtain the distribution of larger fragments represented by residual elements and smaller fragments represented by SPH particles(the mass of a single particle is approximately 8×10-5g),which are not available in the SPH method.Meanwhile,the numerical results obtained by the FE-SPH method of the fragments in Area 1 and Area 3 in Fig.5 are clearly better than those obtained by the SPH method.As the SPH method uses discrete particles to represent the continuum,further fragment identification is needed to determine which particles belong to the same fragment.The FE-SPH method is more convenient and accurate for the subsequent extraction of mass and size information and morphological observation of the fragments.

Fig.9.Comparison with the (a) experimental and (b) numerical results of Li et al.[39] at 52.5 μs.

3.3.Mass distribution of fragments

With the expansion and fracture of the cylindrical shell,the distance between fragments gradually increased,and as shown in Fig.5 (t=70 μs) collisions between fragments rarely occurred;it can be considered that the state of the fragments remained unchanged at this time.MATLAB was used to judge the connectivity between the remaining elements at a stable time,and the elements belonging to the same fragment were grouped into a set.Therefore,the mass distributions of the fragments,shown in Fig.5,were extracted.The extracted fragment mass is drawn as a fragment distribution Mott plot,as shown in Fig.10,providing the cumulative number of fragments greater than a certain mass.A total of 664 fragments were extracted in the form of elements: the maximum fragment mass was 0.67 g and was composed of 8186 elements;the minimum fragment mass was approximately 8×10-5g and contained only one element.The total mass of the extracted fragments was 25.11 g,accounting for 16.3% of the mass of the cylindrical shell(154.31 g),and the remaining mass was converted into particles.

Fig.10.Fragment mass distribution and Weibull fitting.

The mass of fragments in Area 1 of Fig.5 accounted for 10.57% of the total mass of the fragments.The number of fragments in this region was small,and the average mass of the fragments was large,approximately 0.13 g.There were only 34 fragments with a mass greater than 0.2 g,primarily elongated fragments in region 2(such as fragment C).The mass of the fragments in Region 2 was 22.30 g,accounting for 88.79% of the total mass of fragments.The mass of fragments in Area 3 only accounted for 0.64% of the total mass of the fragments.Using post-processing software,the number of elements of any fragment in Fig.5 could be obtained.The mass of any fragment,in Fig.5,could be determined by comparing the number of elements extracted from the resulting file.The masses of four typical fragments are shown in Fig.5.Fig.10 shows the fitting results of the fragment mass data using the Weibull distribution function.The masses data and fitting results are in good agreement-discussed in detail in Section 4.

3.4.Size distribution of fragments

Similar to extracting the mass distribution of the fragments,the size distribution of the fragments,as shown in Fig.5,can be obtained.Fragments recovered through experiments are often characterized by a circumferential width [18].However,as the axial length of the fragments continued to change,large errors might be caused by different measurement positions.Therefore,this study used the arithmetic mean of the following three characteristic dimensions as the characteristic length of a fragment [46]: Dimension A is the maximum size of the fragment,denoted asL1;dimension B is the maximal length on the plane perpendicular to dimension A,denoted asL2;and dimension C is the maximum length in a direction perpendicular to both dimensions A and B,denoted asL3.The characteristic length of the fragment was calculated asL=(L1+L2+L3)/3.This method(size statistics)cannot be used for experimentally created fragments;however,numerical simulations produce fragments whose characteristic length can be accurately described using this method.

Fig.11 shows the total number of fragments in the range of different characteristic lengths.The maximum fragment size was 17.63 mm;the minimum was 0.38 mm.The fragment size was concentrated between 1 -4 mm.The characteristic lengths of typical fragments are shown in Fig.5.The mass of fragment A was similar to that of fragment B,but the characteristic length of fragment B was larger because of its elongated shape.Fig.11 shows the fitting results of the fragment size data using the Rayleigh distribution function;the fragment size distribution and Rayleigh fitting data were in good agreement.In Section 5,the size distribution characteristics of fragments under different internal pressures are discussed in more detail.

3.5.Velocity distribution of fragments

The velocity distribution of the fragments during the expansion of the cylindrical shell is a key parameter in projectile design.The velocity distribution obtained by the numerical simulation was compared with the experimental results of Huang et al.[6];the relative error is shown in Fig.12.The numerical results were consistent with the experimental results.Due to the influence of rarefaction waves,the fragment velocity at both ends of the shell was lower than that in the middle of the shell;the relative error at both ends of the shell was significantly greater than that at the middle of the shell.The reason may be that the numerical simulation excessively considers the influence of the rarefaction wave,resulting in the numerical result of the fragment velocity at both ends being slightly lower than the experimental result.Overall,the relative error was within an acceptable limit of 10%.

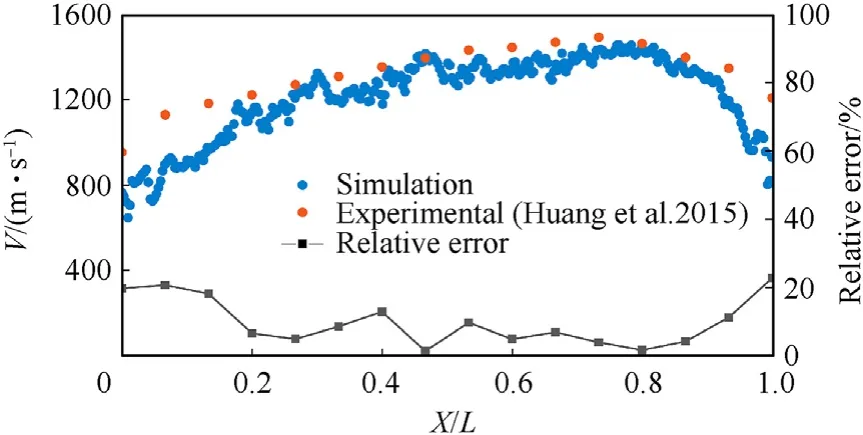
Fig.12.Comparison and relative error of fragment velocity distribution.

Based on the numerical results,this section analyzes the propagation process of the detonation wave,formation process of the cylindrical shell,morphological characteristics,and velocity distribution of the fragments,all in good agreement with the experimental and theoretical analyses.Compared to the SPH method,the FE-SPH method can obtain accurate material boundaries of the fragments,thus providing the conditions for subsequent analysis of the distributions of mass and size.The FE-SPH and fluid-structure interaction method can produce reliable results from simulation of explosively driven metal shells.

4.Statistical analysis of fragment mass distribution

The initial fracture point and fracture path of the explosively loaded axisymmetric cylindrical shells are random;therefore,the statistical distribution of the mass and size of the fragments can be obtained.Mass distribution of fragments is an important issue in the field of explosive technology.Mott and Linfoot[47]proposed a Poisson statistical distribution of the fragment mass,and Grady and Kipp[48]proposed a more widely applicable distribution based on energy

Eq.(6) is the Weibull distribution with two parameters:N(>m)is the cumulative number of fragments with masses greater thanm,N0is the total number of fragments,mis the mass of the fragment,μ is the characteristic mass of the fragments,and α is the distribution scale parameter.When α=1/2,the equation degenerates to a Mott distribution [47].

Based on Eq.(6),nonlinear fitting was performed for the mass data extracted in Subsection 3.3,whereN0=664 is the known quantity;μ and α are the parameters to be fitted;each fragment mass m and its correspondingN(>m) constitute the fitting data.The results are shown in Fig.10.In the fitting results,μ=0.024 g,α=0.735,and the correlation coefficient(Adj.R-Square)was 0.995.The fragment mass distribution extracted by the simulation was in good agreement with the fitted curve,thus demonstrating the accuracy of the numerical results.

The charging cases of three different types of explosives were simulated to study the mass statistical characteristics of the fragments under different explosion pressures.The parameters are listed in Table 5.Fig.13 shows the fragment distribution Mott plot and fitting results based on Eq.(6) for the three different cases listed in Table 5.The fitting parameters μ and α,and the correlation coefficients of the fitting results are listed in Table 5.Section 5 analyzes the relationship of parameterssminands0(Table 5) to their fragment size.

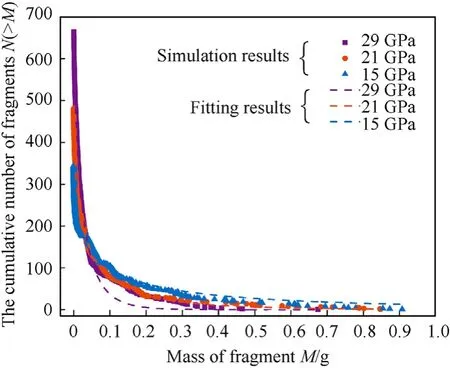
Fig.13.Fragment mass distribution and Weibull fitting under different explosion pressures.

Table 5 Explosive parameters and fitting results under different charge cases.

The numerical results showed that as the explosion pressure decreased from 29 to 15 GPa,the number of fragments decreased from 664 to 345,with the range of the fragment mass distribution increased gradually because,when the explosive pressure is low,the cylindrical shell is not sufficiently fractured,resulting in larger fragments.

In Fig.13,the correlation coefficients of the fitting results for the three cases with different explosion pressures are all above 0.99,indicating that Eq.(6) has a good fitting effect on the mass distribution of the fragments under different characteristics of explosion pressure (loading strain rates).Simultaneously,the characteristic mass μ gradually increased when the explosion pressure decreased,supporting the credibility of the numerical results.

As shown in Table 5,α decreased as the explosive pressure decreased,indicating that the distribution scale parameter α reflects whether the cylindrical shell is sufficiently fractured.The smaller the distribution parameter α,the lesser the shell fracture, and the larger the range of the fragment mass distribution.

5.Statistical analysis of fragment size distribution

Under known material properties and internal loading conditions,predicting the size distribution of fragments is an important topic in the field of expansion and fracture behavior of metal shells.Therefore,it is important to study the statistical size distribution of the fragments.Zheng et al.[49]found that the Rayleigh distribution could describe the size distribution of fragments in the fracture process of one-dimensional ductile metal rings.This distribution can be expressed as

whereN(>s) is the cumulative number of fragments with sizes greater thans,N0is the total number of fragments,smin is the minimum fragment size,ands0is a scale parameter.The probability density function is

As described in Section 4,based on Eq.(7),nonlinear fitting was performed for the size data extracted in Subsection 3.4,whereN0=664 andsmin=0.375 mm are known quantities,s0is the parameter to be fitted,and each fragment sizesand its correspondingN(>s)constitute the fitting data.From the fitting results,s0=2.952 mm.Subsequently,sminands0are substituted into Eq.(8),and the probability density function of the Rayleigh distribution is obtained (Fig.11).The fragment size distribution extracted by the simulation was in good agreement with the Rayleigh distribution,and fragment sizes were concentrated in the range of 1-4 mm.

Furthermore,based on the above analysis,the fragment sizes under the three different charging cases in Table 5 were statistically analyzed,as shown in Fig.14.The simulated fragment size distribution and fitting results are presented in the figure.The minimum fragment sizesminand the scale parameters0are listed in Table 5.It is observed that a higher explosion pressure creates a large number of fragments,in a narrower range of sizes,and a concentrated distribution in fragment size.This is because the cylindrical shell was fully fractured when the explosion pressure was high,resulting in a large number of small fragments.The size distribution of the fragments under different explosion pressures was similar,and most fragments were concentrated in a small size range.

Simultaneously,the Rayleigh distribution curves,under different explosion pressures,were in good agreement with the fragment size distribution.The fitting effect is better when the cylindrical shell fractures more fully,indicating that the Rayleigh distribution is good for fitting the size distribution of the fragments produced by explosively driven cylindrical shells.With a decrease in explosion pressure,the fracture of the cylindrical shell was insufficient,resulting in large fragments.The scale parameters0increased gradually,indicating thats0can reflect the characteristic size of the fragments under different internal explosive loadings.

Fig.15 shows a comparison of the probability density distributions among the three cases.As the explosion pressure decreased,the distribution range of the Rayleigh curve gradually widened,the size range of the concentrated distribution became larger,and the phenomenon of the concentrated distribution gradually weakened,highly consistent with the fragment size distribution in Fig.14.

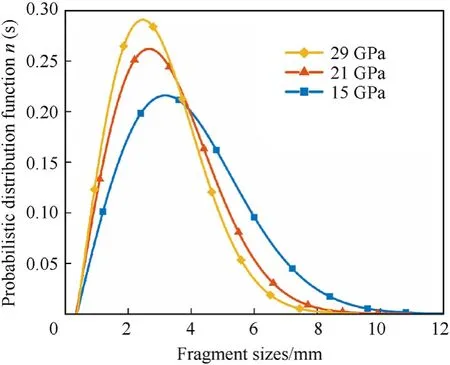
Fig.15.Rayleigh fitting under different explosion pressures.

6.Improvement of the fragment velocity formula

6.1.Establishing the formula

The velocity distribution of the fragments is the basis for projectile design and structural protection.Gurney[1]first proposed a formula,based on energy balance,to predict the initial velocity of the fragments as

The Gurney formula is widely used for calculating the maximum velocity of the fragments.However,the Gurney formula is unsuitable for calculating the velocity distribution of fragments because,in the formula,the rarefaction waves generated at the ends are not considered,which can cause velocity attenuation.Zulkoski [2]developed an exponential correction function based on Gurney’s formula that can be expressed as

wherexis the distance from the detonation end along the casing axis,Lis the casing length,dis the interior diameter of the casing,andv0is the Gurney velocity.

Zulkoski's formula [2] better describes the phenomenon of the reduced velocity near the edges of the cylindrical shell,butv0x(x=0)=0 in Eq.(10) indicates that the fragment velocity at the detonation end is 0,inconsistent with the experimental results.Huang et al.[6]modified the Gurney formula based on Eq.(10),as follows:

whereF1(x/d)is the corrected term at the detonation end,F2((L-x)/d)is the corrected term at the non-detonation end,and A,B,C,and D are the correction coefficients determined by the experimental data.The experimental parameters are presented in Table 6 Case 1.

Table 6 Parameters of two tests.

Huang et al.[6] believed that the fragment velocities near the detonation end were almost determined by the rarefaction wave from the detonation end instead of the non-detonation end.Therefore,Eq.(13) can be assumed to be 1 whenx=0,and the fragment velocity is

wherev0x(x=0)is the fragment velocity at the detonation end measured experimentally in the Ref.[6] andv0is the Gurney velocity.Therefore,coefficientAcan be determined using Eq.(15)

Huang et al.[6] believed that the fragment velocities from the detonation end to the position where the maximum fragment velocity occurs are almost entirely determined by the detonation end rather than the non-detonation end.Therefore,the correction coefficientsAandBcan be determined by the fragment velocities from the detonation end to the position where the maximum fragment velocity occurs.The correction coefficientAis substituted into Eq.(11),andF2((L-x)/d) is considered to be equal to 1.The coefficientBis obtained by fitting the fragment velocities from the detonation end to the position where the maximum fragment velocity occurs using the least-squares method.Whenx=L,Eq.(12)can be assumed to be equal to 1,and the coefficientCcan be obtained in the same manner.Similarly,the correction coefficientCwas substituted into Eq.(11),andF1(x/d)was considered equal to 1.The coefficientDis obtained by fitting the fragment velocities from the non-detonation end to the position where the maximum fragment velocity occurs.Finally,the fragment velocity distribution formula proposed by Huang et al.[6] is

Huang et al.[6]proposed velocity correction terms at both ends of the cylindrical shell and believed that the fragment velocities near one end were only determined by the velocity correction term at this end,providing a more accurate description of the velocity attenuation near the casing edges.However,in the above derivation process,there are some problems in simplifying Eq.(12) and Eq.(13)to reach a value equal to 1 at both ends of the cylindrical shell.In Eq.(16),whenx=L,

In the experiment by Huang et al.[6] (Case 1 in Table 6),the length-to-diameter ratio of the cylindrical shellL/dwas 3.28.Substituting this into Eq.(17),

If the length-to-diameter ratio of the cylindrical shellsL/dis 1,

According to this analysis,when the length-to-diameter ratio of the cylindrical shell is large,F1(L/d) can be considered approximately 1,conforming to the theoretical derivation of Huang et al.[6].However,when the length-to-diameter ratio of the cylindrical shell is small,F1(L/d) can no longer be seen as 1,contradicting the theoretical derivation of Huang et al.[6],thus indicating that Eq.(16)is not applicable to the case of a small length-to-diameter ratio.By adding constant terms to the right side of Eq.(12) and Eq.(13),F1(x/d)(x=L)andF2((L-x)/d)(x=0)are naturally equal to 1.Therefore,Eq.(11)-Eq.(13) are modified as follows:

From Eq.(20)and Eq(21),F1(x/d)(x=L)=F2((L-x)/d)(x=0)=1 can be obtained.Without approximate calculation,the fragment velocities near the detonation end are determined by Eq.(20),and the fragment velocities near the non-detonation end are determined by Eq.(21);it is applicable to cylindrical shells with any length-to-diameter ratios.

6.2.Determining the correction coefficients

The correction coefficientsA,B,C,andDwere determined from the experimental data measured by Huang et al.[6] (Case 1 in Table 6).First,let

wherev0x(x=0)andv0x(x=L)are the fragment velocities at both ends of the cylindrical shell.Whenx=0,Eq.(22) is

Substituting Eq.(23) into Eq.(25)

Substituting Eq.(26) into Eq.(20)

Substituting Eq.(27) and Eq.(28) into Eq.(22),there are only two parametersAandCin the equation.In contrast to Huang et al.[6] fitting the fragment velocities in sections,this study used the least-squares method to fit all fragment velocities along the axis of the cylindrical shell and obtainedA=0.4 andC=0.192.B=0.711 is obtained by substitutingAinto Eq.(26),andD=1.605 is obtained in the same manner.The correction coefficientsA,B,C,andDare substituted into Eq.(22),and the unified formula is obtained as

Although the coefficientsA,B,CandDin two different models(Eq.(11)-Eq.(13),Eq.(20)-Eq.(22)) are solved in different ways,their mathematical meanings are the same,and the positions correspond to each other.CoefficientsAandBare both in the corrected term at the detonation end,and coefficientsCandDare both in the corrected term at the non-detonation end.CoefficientsAandCare both coefficients of the power function,and coefficientsBandDare both in the exponential term.Therefore,we continue to use the coefficientsA,B,CandDin the improved formula without adding new variables.

6.3.Verification and discussion

Fig.16 shows the comparison between the two equations (Eq.(16)and Eq.(29))and the experimental results of fragment velocity for two different cases.Case 1 is the basic experimental data used to determine the correction coefficients of the two equations;Case 2 was used to validate the general applicability.The experimental results were obtained from Ref.[6],and the structural parameters are listed in Table 6.The length-to-diameter ratios of the cylindrical shells in the two cases are 3.28 and 3.27,respectively;they are both large length-to-diameter ratios.Fig.16 shows that our calculated results are consistent with the experimental data clearly reflecting the influence of the rarefaction waves at both ends of the cylindrical shell on velocity attenuation.However,Huang et al.[6]divided the fragment velocity into two segments from the position of the maximum velocity.Eq.(12) and Eq.(13) were used for least-squares fitting,resulting in the calculation result of Eq.(16)being larger than the experimental result.Compared to Eq.(16),the calculation result of Eq.(29) is more consistent with the experimental data.In addition,no approximation was made in the derivation of Eq.(29),applicable to cylindrical shells with any length-to-diameter ratios.Therefore,Eq.(29) has higher accuracy and wider applicability.

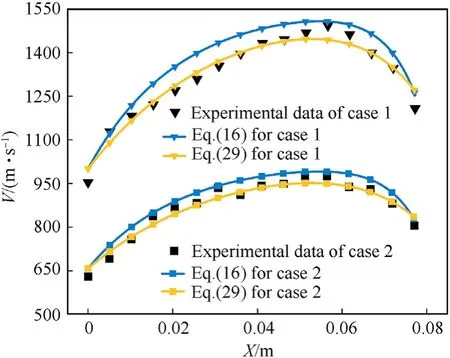
Fig.16.Comparison of Eq.(16) and Eq.(29) with the two experimental results.

7.Discussion

The expansion and fracture of metal shells subjected to internal explosive loading are highly complex multiscale problems.At the microscale,the type of explosive,material properties,and geometric characteristics determine the fracture point,fracture mode and fracture process of the shell;they also determine the macroscopic characteristics of the explosion such as the distributions of velocity,mass,and size of the fragments.Based on the experimental and numerical results,researchers proposed multiple failure modes for the expansion of cylindrical shells,including tensile failure initiating from the outer surface of the shell,shear failure developing along the maximum shear stress surface,mixed tensileshear failure,and micro-crack failure initiating in the middle of the cylindrical shell [50].

In this study,the FE-SPH adaptive method and the fluid-structure interaction method were used to simulate the expansion and fracture of the AISI1045 steel cylindrical shell filled with Composition B.The results showed that the cracks initiated at the inner surface of the casing and extended to the outer surface along 45°or 135°with strain localizations,finally forming shear fractures.Typical elongated fragments,with clear shear fractures on both sides,were extracted from the numerical results,as shown in Fig.5.Simultaneously,the mass and characteristic length of any fragment at a stable time can be determined through fragment identification,which is helpful for the subsequent analysis of the damage effect of the fragments.In addition,we statistically analyzed the mass and size distributions of the fragments under different explosion pressures.We examined the applicability of the distribution functions and the physical meaning of the characteristic parameters.Our analysis is applicable to research on the fragment distribution of warheads with different geometric structures (such as shells with variable thicknesses) and different initiation modes (such as eccentric single-point initiation and multipoint initiation),critical for the structural design and safety assessment of the new warhead.

Due to the limitation of the calculation scale,the number of radial meshes along the cylindrical shell is limited,making the shear localization in the numerical results unclear.The axial displacement and velocity are one order of magnitude less than observed in the radial direction during the expansion of the cylindrical shell;therefore,the mesh can be refined and modeled as a one-dimensional plane strain problem.

Fig.17 shows the numerical results of the expansion and fracture of the cylindrical shell when the simulation is simplified to a planestrain problem.The simulation method and material parameters were the same as those described in Section 2,with a modified calculation model.Fig.17(a) shows the parameters used in the calculation model (of the case in Table 1) after refining the mesh.The cylindrical shell was divided into 100,320 hexahedral elements with a side length of approximately 50 μm.Only a single-layer mesh was used for the calculation (theZ-direction length of the shell was 50 μm);Z-direction constraints were imposed on the entire model.Fig.17(b) shows the top view of the cylindrical shell after the SPH particles were hidden.Fig.17(c)shows a detailed view of the development of the equivalent plastic strain formed by the shear fracture.The results show that the cracks first initiate at the inner surface of the cylindrical shell and then expand at 45°or 135°from the radial direction to the outer surface.The results are similar to the results depicted in Fig.6 and Fig.7.However,compared to Fig.6 and Fig.7,the macroscopic fracture in Fig.17 is clearer,and the phenomenon of strain localization is more discernible.

Fig.17.Plane strain model and numerical results: (a) Plane strain model;(b) t=15 μs;(c) t=7 μs, t=8 μs; t=9 μs, t=10 μs, t=11 μs (From the left to the right of (c)).

In addition,the adaptive method supports the calculation of temperature by adding the corresponding parameters to the material models.In subsequent research,the meshes can be refined,and the temperature change during the expansion can be considered to simulate the adiabatic shear zone.Our analysis shows that the simulation method used in this study is suitable for the mesomodeling analysis of explosively driven cylindrical shells.Thus,our simulation method can be applied to investigate the mesomechanism of fracture and fragmentation of the shell.

The accurate calculation of the velocity distribution of fragments is of great significance in the design of explosives.In this study,based on the work of Huang et al.[6],the Gurney formula was further modified to obtain a more accurate formula for calculating the velocity distribution of fragments.The modified formula is suitable for cylindrical warheads with any length-to-diameter ratios.At present,most formulas can predict the velocity distribution of cylindrical shells;however,they are difficult to apply to warheads with more complex structures.Establishing engineering formulas for the velocity distribution of fragments in general warheads will be an important direction for future research.

8.Conclusions

In this study,the FE-SPH adaptive method and the fluid-structure interaction method were used to perform a threedimensional numerical simulation of the expansion and fracture of the AISI1045 steel cylindrical shell filled with Composition B.The simulated morphology and velocity distribution of the fragments were consistent with the experimental results,thus verifying the reliability of the calculation method.Based on the numerical results,the propagation process of the detonation wave,fracture and fragmentation mechanisms of the metal shells,and mass and size distribution characteristics of the fragments were analyzed.The distribution formula of the fragment velocity was improved via theoretical analysis.The following conclusions were drawn from this study.

(1) After the charge is detonated from the center point of the end,the curvature of the detonation wavefront decreased as the detonation wave propagated.The detonation wave was transformed from a spherical wave to a plane wave,and the angle of oblique incidence on the shell gradually increased.Finally,the explosion entered a stable sliding detonation stage.As the shock wave reflected back and forth between the inner and outer surfaces,the pressure distribution inside the shell alternated between a tensile and a compression wave.

(2) The fracture mode of the AISI1045 steel cylindrical shell under a high explosion pressure (Composition B) was primarily shear fracture.During the expansion process,the equivalent plastic strain near the inner surface of the cylindrical shell was always at its maximum.The cracks started at the inner surface,expanded to the outer surface along the direction of the maximum shear stress (45°or 135°),and finally formed a shear fracture.

(3) The mass distribution of the fragments conformed to the Weibull distribution with two parameters;the distribution parameter α reflects whether the cylindrical shell was sufficiently fractured.A smaller distribution parameter α implies that the explosion pressure was lower causing lesser fracture of the shell and larger distribution of the mass of the fragments.

(4) The size distributions of the fragments under different explosion pressures were similar and could be described by the Rayleigh distribution.The Rayleigh distribution fitting effect is better at higher explosion pressures because the cylindrical shell expands fully and there are larger number of fragments.The scale parameters0reflects the characteristic length of fragments under different internal explosive loadings.With a decrease in the explosion pressure,the scale parameters0increased,the distribution range of the Rayleigh curve widened,and the phenomenon of the concentrated distribution weakened.

(5) The velocity distribution formula for the shell fragments under central-point initiation was modified.The new formula has higher accuracy and is suitable for calculating the fragment velocity of cylindrical shells with any length-to-diameter ratios.It can show the influence of rarefaction waves(at both ends of the shell) on velocity attenuation.

The fracture mechanisms of explosively loaded shells are extremely complex because of the randomness of the fracture point and fracture path.Through numerical simulation,the entire process of the expansion and fracture of the cylindrical shell and the details that cannot be observed in experiments can be obtained.In our future research,the fracture process will be modeled on a microscale,and the fracture mechanism will be analyzed in more detail.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No.11872118,11627901).The first author would like to thank Dr.He QG for his assistance with the FESPH adaptive method.