保斜渐近线和垂直渐近线的连分式插值
2023-10-09胡云飞赵前进
胡云飞, 赵前进
(安徽理工大学 数学与大数据学院, 安徽 淮南 232001)
连分式是一个十分古老的数学分支学科, 但是连分式插值与逼近[1]是一种新的非线性数值计算工具, 它提供了一种新的非线性数值计算方法, 连分式在工程技术领域得到了应用[2-4], 近年来连分式成功地应用于计算机辅助几何设计和数字图像处理等领域[5-6]. Thiele型连分式插值[1, 7]是一种有理插值方法[8], 为函数的连分式展开提供了强有力的工具. 在工程技术中经常遇到一些具有斜渐近线和极点的函数, 采用多项式或者传统的Thiele型连分式作为逼近工具是不合适的, 在逼近函数时无法保持被插值函数的斜渐近线, 也无法区分极点以及极点的重数, 逼近效果不一定十分理想. 通过研究连分式插值有理分式最高次项系数与函数极限之间的关系, 构建保斜渐近线和垂直渐近线的连分式插值算法, 证明新算法的存在唯一性[9], 给出误差分析[10-11]和数值例子证明新算法的有效性.
1 Thiele型连分式插值
设被插值函数y=f(x),x0,x1, …,xn是被插值函数y=f(x)的(n+1)个互异的插值节点,yi=f(xi)(i=0, 1, …,n)是插值函数y=f(x)在插值节点处的函数值.
称如以下公式(1)形式的连分式:
(1)
为Thiele型连分式, 其中Pn(x),Qn(x)为有理分式的分子分母.
式(1)中
bi=φ[x0,x1, …,xi],i=0, 1, …,n,
(2)
令
φ[xi]=yi,i=0, 1, …,n,
(3)
(4)
(5)
称由以上式(2)~(5)确定的φ[x0,x1, …,xl]为函数f(x)在点x0,x1, …,xl处的l阶逆差商, 且满足下列条件
Rn(xi)=yi,i=0, 1, 2, …,n.
设P-1=1,P0=b0,Q-1=0,Q0=1, 则对n≥1有连分式的三项递推关系[12]
(6)
由连分式三项递推关系可知多项式Pn(x)和Qn(x)的最高次项系数和次最高项系数具有以下系数关系[13]:
当n为奇数时
L(Pn(x))=1,
(7)
L(Qn(x))=b1+b3+…+bn,
(8)
L′(Pn(x))=b1b0-x0+b3(b0+b2)-x2+…+bn(b0+b2+…+bn-1)-xn-1,
(9)
L′(Qn(x))=0+b3L′(Q2(x))-b1x2+…+bnL′(Qn-1(x))-(b1+b3+…+bn-2)xn-1;
(10)
当n为偶数时
LPn(x)=b0+b2+…+bn,
(11)
LQn(x)=1,
(12)
(13)
(14)


(15)
易证明上式多项式最高次项系数和次最高次项系数关系:
L(d(x))=1,
(16)
(17)
设
(18)
由式(7)~(14)可得
当n+1为奇数时
L(P1, n+1(x))=b1+b3+…+bn+1,
(19)
L(Q1, n+1(x))=1,
(20)
L′(P1, n+1(x))=b3L′(P1, 2(x))-b1x2+…+bn+1L′(P1, n(x))-(b1+b3+…+bn-1)xn,
(21)
L′(Q1, n+1(x))=b3b2-x2+…+bn+1(b2+b4+…+bn)-xn;
(22)
当n+1为偶数时
L(P1, n+1(x))=1,
(23)
L(Q1, n+1(x))=b2+b4+…+bn+1,
(24)
L′(P1, n+1(x))=b2b1-x1+b4(b1+b3)-x3+…+bn+1(b1+b3+…+bn)-xn,
(25)
L′(Q1, n+1(x))=0+b4L′(Q1, 3(x))-b2x3+…+bn+1L′(Q1, n(x))-(b2+b4+…+bn-1)xn.
(26)
构造连分式插值
(27)
满足以下条件
r*(xi)=c(xi)=yid(xi),i=0, 1, …,n,
(28)
由式(15)(18)(27)可得预给极点的连分式插值
(29)
2 保斜渐近线和垂直渐近线的连分式插值算法

由式(15)(18)(29), 可得
(30)
使之满足
(31)
式(30)中
φ[xi]=c(xi)=yid(xi),i=0, 1, …,n-1,
易证明
当n+1为奇数时
(32)
当n+1为偶数时
(33)
由于xn,xn+1未知, 故无法通过逆差商公式计算得到bn=φ[x0,x1, …,xn],bn+1=φ[x0,x1, …,xn+1].
由式(7)(8)(11)(12)(30)可得
当n+1为奇数时
(34)
由式(34)计算可得
(35)
当n+1为偶数时
(36)
由式(36)计算可得
bn+1=A-b0-b2-…-bn-1.
(37)
由式(16)(17)(18)(30)可得

(38)
由式(16)~(26)可得
当n+1为奇数时
bn=

(39)
当n+1为偶数时
bn=

(40)
3 存在唯一性证明
定理1:设
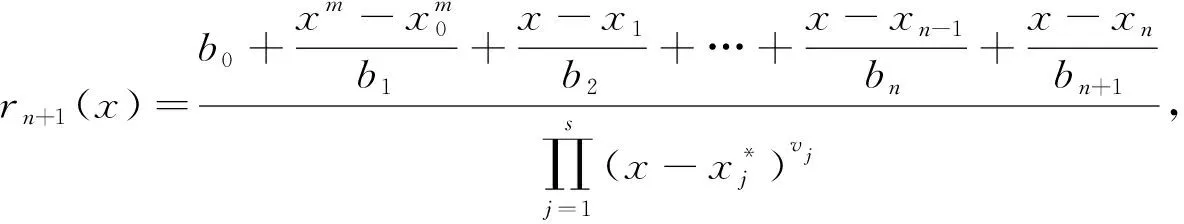

证明:利用逆差商的定义可得:
定理2:有理插值问题(30)(31)若存在解, 则解是唯一的.
证明:由式(30), 设



由

得

下设

则有
由式(35)(37)可得

同理, 由式(39)(40)可得

于是
唯一性即证.
4 误差分析
定理3:设插值节点{x0,x1, …,xn-1,xn}⊂(a,b),y=f(x)在(a,b)上有n阶的导数, 若



且有
其中ωn(x)=(x-x0)(x-x1)…(x-xn-1),x0,x1, …,xn-1及x的最小开区间表示为Ι(x0,x1, …,xn-1,x).
证明:设E(x)=f(x)Qn+1(x)-Pn+1(x), 则有rn+1(xi)=yi(i=0, 1, …,n-1), 得
E(xi)=0,i=0, 1, …,n-1,
因此
E[x0,x1, …xk]=0,k=0, 1, …,n-1,
E[x0,x1, …xk]表示函数E(x)在点x0,x1, …xk的k阶差商.
利用Newton展开式可得

因此
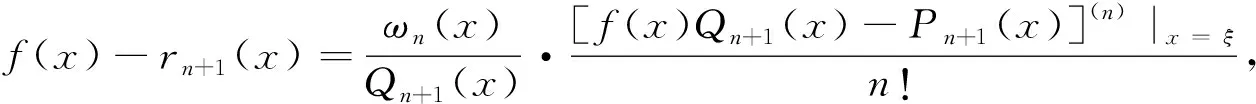
同时
5 数值例子
证明:由式(28)可得r*(x0)=5.25385602,r*(x1)=19.29152412,r*(x2)=49.21779912,r*(x3)=101.13430700, 由式(36)可得m=3.
将以上数据代入式(35)可知

将b5代入式(39), 得
b4=

将b4,b5代入保斜渐近线和垂直渐近线的连分式算法式(30), 得

(41)
将式(41)化简为有理函数, 得
(42)
显然
证毕.
若使用传统的Thiele型插值连分式, 由式(1), 得

(43)
将式(43)化简为有理函数, 得
(44)
被插值函数y=f(x)的图像和斜渐近线与插值函数r5(x)的函数图像如图1所示.

图1 插值函数与被插值函数图像
由图1可知, 保斜渐近线和垂直渐近线的连分式插值在逼近具有斜渐近线和极点的函数时具有较好的逼近效果, 可以保持被插值函数的斜渐近线和垂直渐近线.
计算被插值函数y=f(x)与插值函数r5(x)、R3(x)在某些点处函数值差的绝对值, |f(x)-r5(x)|和|f(x)-R3(x)|的误差函数图像如图2所示.
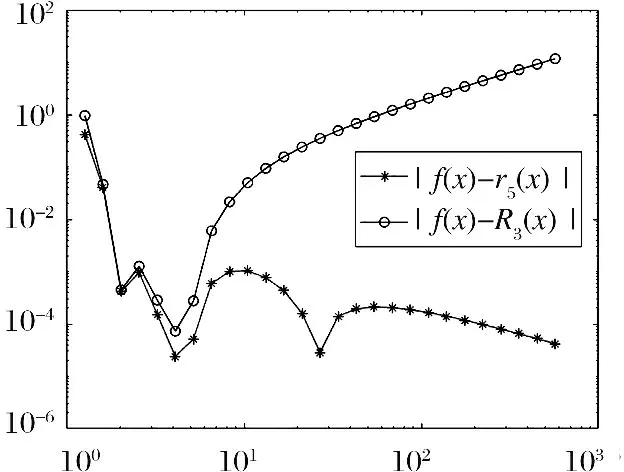
图2 误差函数图像
由图2可知, 保斜渐近线和垂直渐近线的连分式插值在逼近具有斜渐近线和极点的函数时相比于传统的Thiele型连分式插值具有更小的误差.
6 结论
文章研究保斜渐近线和垂直渐近线的连分式插值问题, 通过对每个插值函数值乘以一个确定的数以及连分式的有理分式的分子多项式和分母多项式的最高次项和次最高次项系数存在的恒等关系, 构建了保斜渐近线和垂直渐近线的连分式插值算法, 证明了新算法的存在唯一性, 给出了误差分析并通过数值例子证明了新算法的有效性.
