状态空间有限元法分析固支叠层结构热应力
2023-10-08沈宇昂梁拥成郑兴伟韩志林
沈宇昂,梁拥成,郑兴伟,韩志林
(东华大学 理学院, 上海 201620)
近年来,强度高且性能好的复合叠层材料被广泛用于工程界,但叠层板之间为协调变形,各层之间必然存在相互制约的作用力,这便是层间应力,准确计算层间应力对于工程界而言意义重大。虽然有限差分法、有限元法、边界元法等都是可以计算层间应力的数值方法,但是使用状态空间法分析计算叠层结构的力学特征,具有计算精度较高、计算量较小和计算所需的时间较短等优点。输入变量、状态转移矩阵和输出变量是状态空间法的3部分。叠层结构交界面上已知的位移和应力分量组成了输入变量,材料的属性决定了状态转移矩阵,而各个交界面上未知的位移、应力分量组成了输出变量。状态空间法已被用于许多力学问题:范家让[1]提出将状态空间法运用于板壳问题;谢霁明[2]和郭增伟等[3]将状态空间法用于计算桥梁颤振分析;欧阳光等[4]将状态空间法用于研究吊杆张拉力分析。状态空间法不仅可以计算力学物理量,还可以用于检验材料性质或材料建模等,如:Wu等[5]使用状态空间法来检验弹性层表面的不稳定性;王延灵等[6]将状态空间法用于大迎角气动力学建模。
受有限元思想的启发,Sheng等[7]提出状态空间有限元法,此方法在叠层结构的水平方向采用有限元法离散位移、应力分量,而在垂直方向仍然采用状态空间法求解;Wu等[8]提出沿叠层结构的水平方向采用样条插值法,而在垂直方向使用状态空间法,这也可以较为准确地计算出叠层结构的物理量。
现有研究已将状态空间法用于分析热应力问题。例如:邹贵平等[9]在分析层合圆柱厚壳热应力问题时将状态空间法与打靶法结合;盛宏玉等[10]引入状态空间理论并应用差分格式分析了一维杆的纵向热弹性动力响应瞬态问题;韩志林等[11]将状态空间法用于分析叠层结构热应力问题;陈新宇等[12]使用状态空间法研究受轴对称温度载荷的功能梯度圆筒问题,得到正确、有效的数值解。此外,状态空间法可以与有限元法结合,其他计算方法也可以与状态空间法耦合应用,例如:Benedetti等[13]将状态空间法与快速边界元法结合,求得压电黏结材料的应力场;Cheng等[14]将状态空间法与边界元法结合,求解功能梯度材料的弹性力学问题。
通常研究人员会选择在水平面使用Lagrange单元来离散物理场,例如Wu等[15]使用高阶Lagrange插值来计算盐度,但由于本文研究的叠层结构两固支端的应力变化较为剧烈,使用Lagrange单元离散物理场不一定能准确描述应力变化。因此本文采用更光滑的B样条单元离散物理场,从而提出等几何的B样条状态空间法。B样条插值也广泛用于力学分析,如:Simpson等[16]结合B样条插值与边界元法,进行弹性力学分析;范纪华等[17]使用B样条插值对旋转悬臂梁进行动力学分析。
同时,本文分别采用通解法和精细积分法求解状态空间方程,以研究何种方法更适用于固支问题。本文数值算例表明,位移的数值结果在2种离散方案及2种求解方案情况下均较为精准,而在计算应力时,B样条结果精度更高。虽然精细积分法和通解法均能较快完成二维状态空间方程的计算,其中精细积分法由于采用高效迭代的技术,其计算时长少于通解法。
1 二维模型变分原理
Lagrange单元离散和B样条单元离散叠层结构如图1所示,由M(M=3)层各向同性材料所组成的叠层结构,不同层的弹性模量E、泊松比μ以及热膨胀系数α均不同。横向位移u和纵向位移v分别为x和y方向的位移;l和h分别为整体材料的长度和高度;ΔQ为温度荷载,叠层结构两侧均受固支约束。由于材料的几何形状及温度荷载均对称,故只截取左半边进行分析。边界条件:x=0的边的位移u=v=0;x=l/2的边的位移u=0,应力σxy=0。
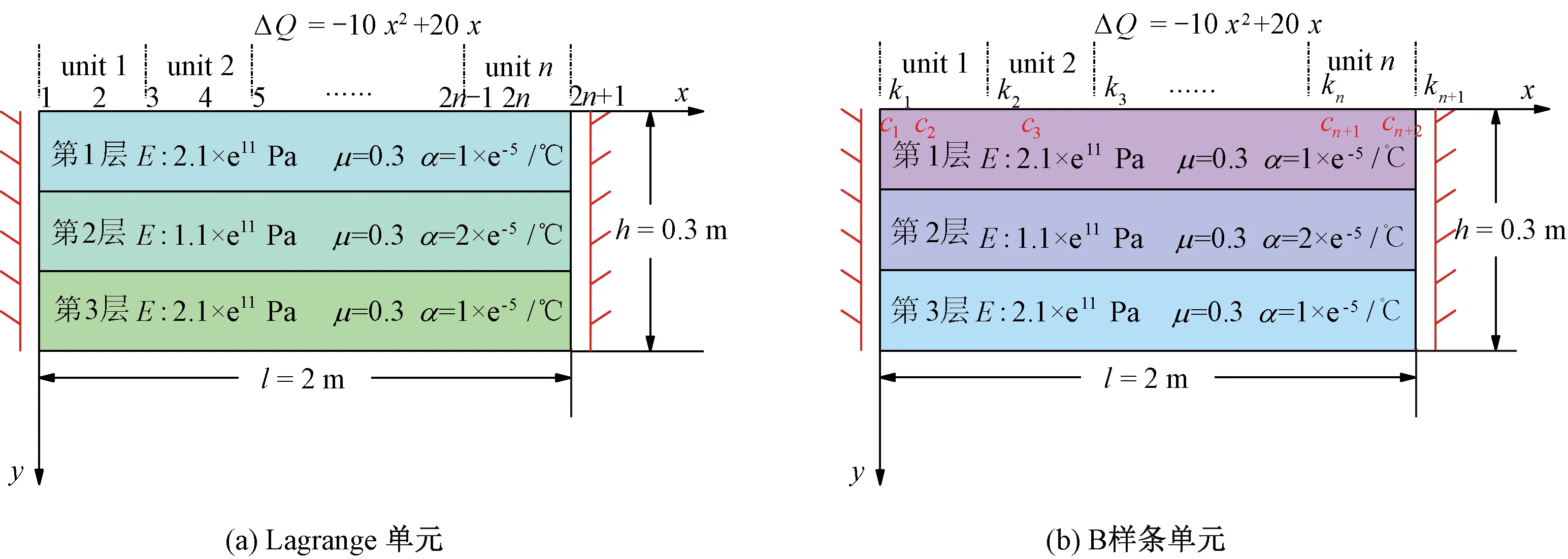
图1 Lagrange单元和B样条单元离散叠层结构Fig.1 Discretization of the laminated structure by Lagrange and B-spline elements
根据Hellinger-Reissner[18]变分原理,以位移和应力满足边界条件的假设对叠层结构中的任意一层建立二维弹性力学中的平衡方程式(1)和几何方程式(2)。
(1)
(2)
本文仅在叠层结构第一层最上方划分单元,分别通过Lagrange插值和B样条插值来划分单元。以Lagrange二次元为例,在第一层材料的上方划分n个单元,产生了2n+1个节点(见图1(a))。
Lagrange插值公式为
(3)
式中:w为lagrange公式局部坐标系的坐标,wi为第i个lagrange节点的坐标zi为对应的函数值;pk(w)为第k个基函数,在wk处值为1,其余插值点处值为0;Bk为Lagrange插值法产生的所有节点的集合;Ln(w)为总体插值函数,其经过每一个插值点。
B样条曲线中的递推形B样条基函数[19]多被用于CAD(computer aided design)。B样条与数值算法的结合可以直接套用CAD模型,从而大幅减少划分单元的时间。B样条插值法与Lagrange插值法有所不同,最显著的特点在于B样条不满足Kronecker-Delta特性。B样条的基函数递推式如式(4)和(5)所示,其一阶导函数如式(6)所示。
(4)
(5)
(6)
式中:wi+1和wi+p分别表示第i+1和第i+p个控制节点的坐标;Ni,0为0阶B样条的第i个基函数;Ni,p表示p阶B样条的第i个基函数。由式(4)和(5)可知,p阶B样条基函数可由0阶基函数迭代得到。
B样条插值法的一大特点在于B样条插值需要节点向量和控制点共同作用,节点向量确定B样条的基函数,而控制点确定B样条曲线的形状。本文所求物理量反映控制点所具有的各分量,而真实物理量需根据B样条形函数进一步插值得到。k1,k2,…,kn+1为B样条的节点,每两个相邻节点之间为一个单元;c1,c2,…,cn-2为控制点,对二次插值来说,相邻的3个控制点作用在一个单元内(见图1(b))。
两种单元对应的离散方法类似,以位移u及二次元为例,u=N1(x1)u1+N2(x2)u2+N3(x3)u3。
对于本文所探讨的热应力问题,其物理场方程为
ε=Sσ+J
(7)
式中:S为各向同性材料的柔度矩阵;J=[αQαQ0]T,Q为每层材料的温度,℃。
将式(7)代入式(2),并将σxx和σxy、σyy拆分,可得到
(8)
αK)dΩ=0
(9)
式中:S1、S2、S3分别为柔度矩阵S中的元素。将离散每一层材料的界面物理量分别代入式(9)得到式(10),代入式(8)并与式(1)进行合并得到式(11)。
(10)
(11)
引入边界条件至式(10)和(11),并由变分理论等价得式(12)。
Dfsf=EfRf-GfK
(12)
(13)
联立方程式(12)和(13),消去sf得到式(14)。
(14)
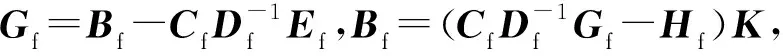
计算由式(13)得到微分方程时,需要保障最后的系数矩阵是正定的,故要求未知状态量中位移和应力分量的个数相同。然而通过固支边界条件可知,每层固支边都存在多余未知量σxy和σyy。为保证正定性,利用式(15)消除这两个分量。
(15)
式中:K1是节点1处的温度。
将式(15)计算所得的关系式代入式(14)中,形成任意一层的非齐次状态方程如式(16)所示。
(16)
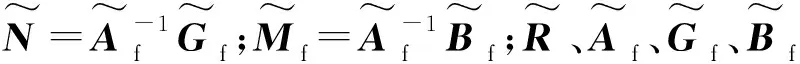
2 状态方程的求解
2.1 通解法
对于叠层结构中的第i层,得到如式(16)的非齐次状态方程为
(17)
式中:Ri为状态方程中的状态向量,是仅关于y的函数;Ni为状态方程中的状态矩阵;Mi为状态方程中的输入矩阵。
根据状态方程的通解,并令y=yi,可得:
(18)
式中:Di(y)为状态方程中的状态转移矩阵;hi为第i层材料的厚度。
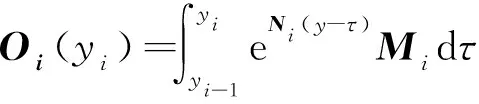
Aixi=bi
(19)
式中:Ai为第i层材料的系数矩阵;bi为已知状态分量组成的向量;xi为未知状态分量组成的向量。
同样的,第i+1层材料也可以形成线性方程式(20)。
Ai+1xi+1=bi+1
(20)
由第i层和第i+1层间界面的连接条件表示为
pi+1(yi)=pi(yi),qi+1(yi)=qi(yi)
(21)
式中:pi+1(yi)和pi(yi)分别为第i+1层上端界面和第i层下端界面的位移分量;qi+1(yi)和qi(yi)分别表示第i+1层上端界面和第i层下端界面的应力分量。因此,
Ri+1(yi)=Ri(yi)
(22)
联立各材料的控制方程,最终得到系统方程式(23)。
Aax=b
(23)
式中:Aa为各层材料的系数矩阵组成的总系数矩阵;x为全部的未知分量组成的向量;b为全部已知分量组成的向量。
2.2 精细积分法
若叠层结构的第i层足够薄,式(17)中矩阵Ri(y)可表示为(Ri(v1)+Ri(v2))/2。其中,v1和v2分别为第i层材料上、下表面沿y轴的坐标。若第i层并非足够薄,可以将该层材料分成Ki=2k层材料,各个子层的厚度为Δi=hi/2k,则Ri(y)可以在足够薄的子层中取平均值来处理。例如,对i层进行过2k次划分之后的第一个子层在式(14)的左右两端同时做积分,可得
(24)
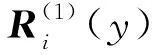
(25)
整理、移项后得
(26)
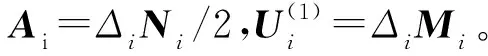
(27)
对第i层各个子层进行平均近似。同时注意到各子层之间的连续条件为
(28)
从第一个子层迭代到最后一个子层,可得
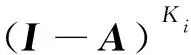
(29)
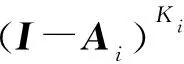
最后和通解法一样联立控制方程,可得到系统方程式(30)。
(30)
3 数值算例
本算例中所用模型为各向同性材料组成的叠层结构(如图1),长l=2m,高h=0.3m,每一层材料的高度均为0.1 m。x=0 m和x=1 m的两边均为固支约束。沿y轴正方向的材料参数分别为弹性模量E1=2.1×1111Pa,E2=1.05×1011Pa,E3=2.1×1111Pa;泊松比均为μ=0.3;热膨胀系数α1=1×10-5℃,α2=2×10-5℃,α3=1×10-5℃。叠层结构受到的温度荷载为ΔQ=-10x2+20x。
由于结构的形状、性质和温度载荷都是对称的,所以本文中仅分析左边一半结构。使用状态空间有限元法计算,并将结果与有限元Abaqus的数值结果作对比。
算例中分别使用二次Lagrange单元离散和二次B样条单元离散该叠层结构。B样条离散法取节点向量为{0,0,0,0.05,0.1,0.15,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,1,1},控制点的坐标为{0,0.025,0.075,0.125,0.175,0.25,0.35,0.45,0.55,0.65,0.75,0.85,0.95,1};Lagrange单元离散法用以比较的节点坐标与B样条单元离散法的控制点坐标相同。而有限元方法采用Quad(四边形)单元划分网格,节点的间距为0.02 m。
进行不同求解算法的收敛性和运算速度的分析,分别使用二次Lagrange单元离散法和二次B样条单元离散法进行对比。表1为不同求解算法下Lagrange单元离散法计算第1、2层交界面点P1(0.3,0.2)的位移u的结果。由表1可以看出,不同算法条件下,Lagrange单元离散法均不需要划分很多子层就能收敛。随着子层数增多,通解法计算速度明显变慢,而精细积分法计算所需时间稳定在0.01 s左右,速度显著快于通解法。通解法和精细积分法结果均与有限元参考解吻合良好。

表1 Lagrange单元离散法使用不同解法计算点P1(0.3,0.2)的位移u的结果Table 1 Results of displacements u at point P1 (0.3,0.2) by Lagrange discretization with different solving schemes
表2为不同求解算法下B样条单元离散法计算第1、2层交界面点P2(0.25,0.20)的位移u结果。使用通解法计算时,B样条单元离散法并不能随着子层数的增多收敛到一定值,并且计算结果相较有限元法有较大差距。而使用精细积分法计算时,B样条单元离散法的计算结果能收敛到一个较为准确的结果。同样精细积分法计算的速度显著快于通解法。
对两种插值法进行比较分析,由于Lagrange单元离散法在单元边界处仅具有C0连续,而本文所采用的二次B样条单元离散法的连续性为C2,所以B样条单元离散法的结果较Lagrange单元离散法更为精确。
算例均采用精细积分法求解状态方程,k取值为4,图2(a)为使用Lagrange单元离散法和B样条单元离散法计算得到的第1、2层间界面位移u与有限元计算结果的对比。图2(b)同样为两种离散法计算的相同点的位移v的结果与有限元法的对比。图3为使用Lagrange单元离散法和B样条单元离散法计算得到的第1层上界面的位移u和v与有限元法的对比。图2、3中:d均表示节点和叠层板最左边的距离,单位为m;FEM表示有限元计算结果,SSM-L表示Lagrange离散单元状态空间法计算的结果;SSM-B表示B样条离散单元状态空间法计算的结果。由图2、3可知:顶层和交界面的横向位移u均小于0,即叠层板在横向上受到挤压后收缩,形变程度先大后小;顶层和交界面的纵向位移v均大于0,即叠层板在纵向上受到挤压后凸起,形变程度越来越大;两种插值方法得到的位移都能与有限元法吻合。
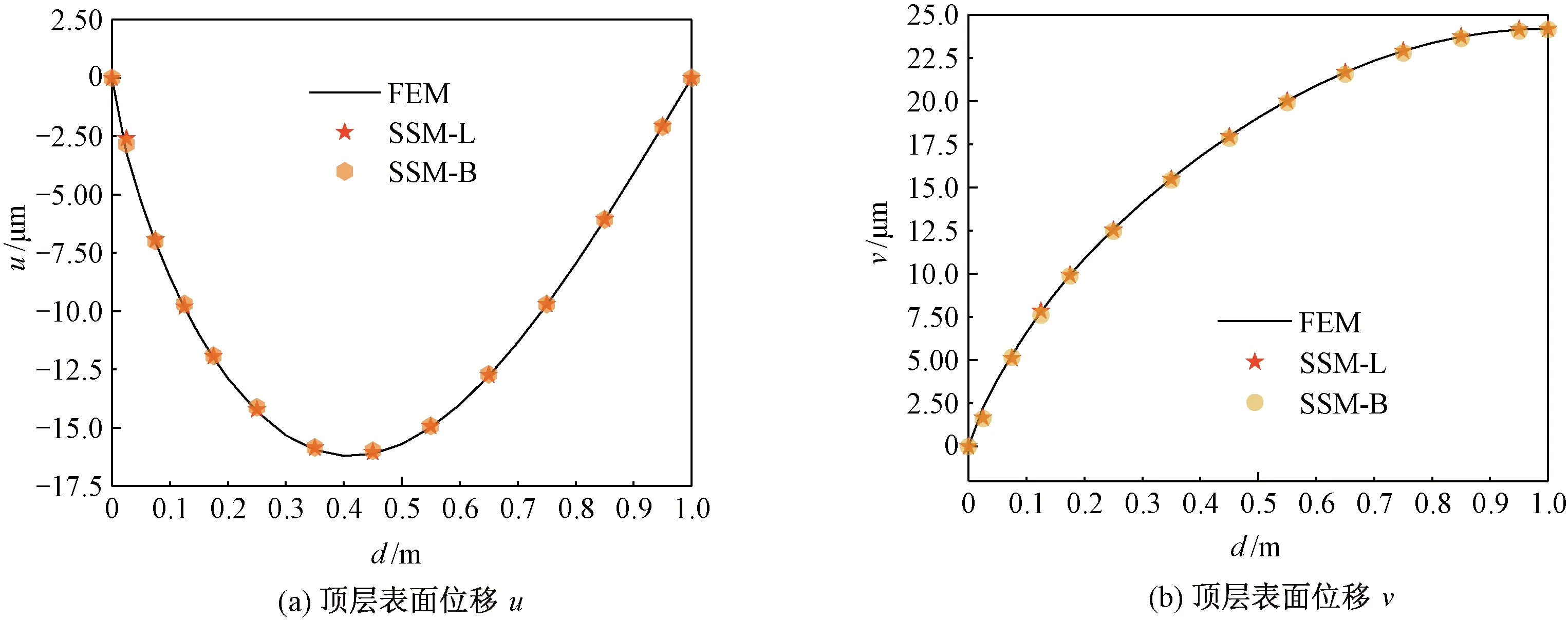
图3 不同离散法顶层表面位移u和vFig.3 Displacements u and v on the top layer by different discretizations
图4(a)为使用Lagrange单元离散法和B样条单元离散法计算得到的第1、2层界面应力σxy的结果与有限元结果的比较。图4(b)同样为两种离散法计算的应力σyy与有限元结果的对比。由图4(a)可知:0≤d≤0.1m则σxy变大;d≥0.1 m后σxy变小。由图4(b)可知:0≤d≤0.3 m则σyy变化剧烈;而d≥0.3 m后σyy变化较为平稳,但在固支端应力变化较为剧烈。两种离散方案的数值结果均能够较好与有限元结果吻合,Lagrange单元离散法计算σyy(图4(b))的结果比B样条单元离散法的计算结果精度差。但B样条单元离散法在节点处的连续性更优。
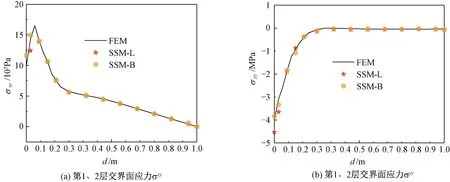
图4 不同离散法下第1、2层交界面应力σxy和σyyFig.4 Stresses σxy and σyy on the interface of 1st and 2nd layer by different discretizations
状态空间法求正应力σxx需要利用已求得的分量进一步计算。
σxx=D-1(ER-GQ)
(31)
式中:常数矩阵D、E、G依据材料参数确定,即第1层材料的下界面和第2层材料的上界面各节点受到的正应力σxx有差异。
图5为使用Lagrange单元离散法和B样条单元离散法计算的顶层上表面应力σxx的结果。图6为使用两种离散方法计算第1、2层界面处的σxx,并与有限元结果对比。由图5可知,顶层面的σxx也是在边界处的变化即为剧烈,而其他区域较为平稳。

图5 不同离散法下最顶层面应力σxxFig.5 Stresses σxx on the top layer by different discretizations
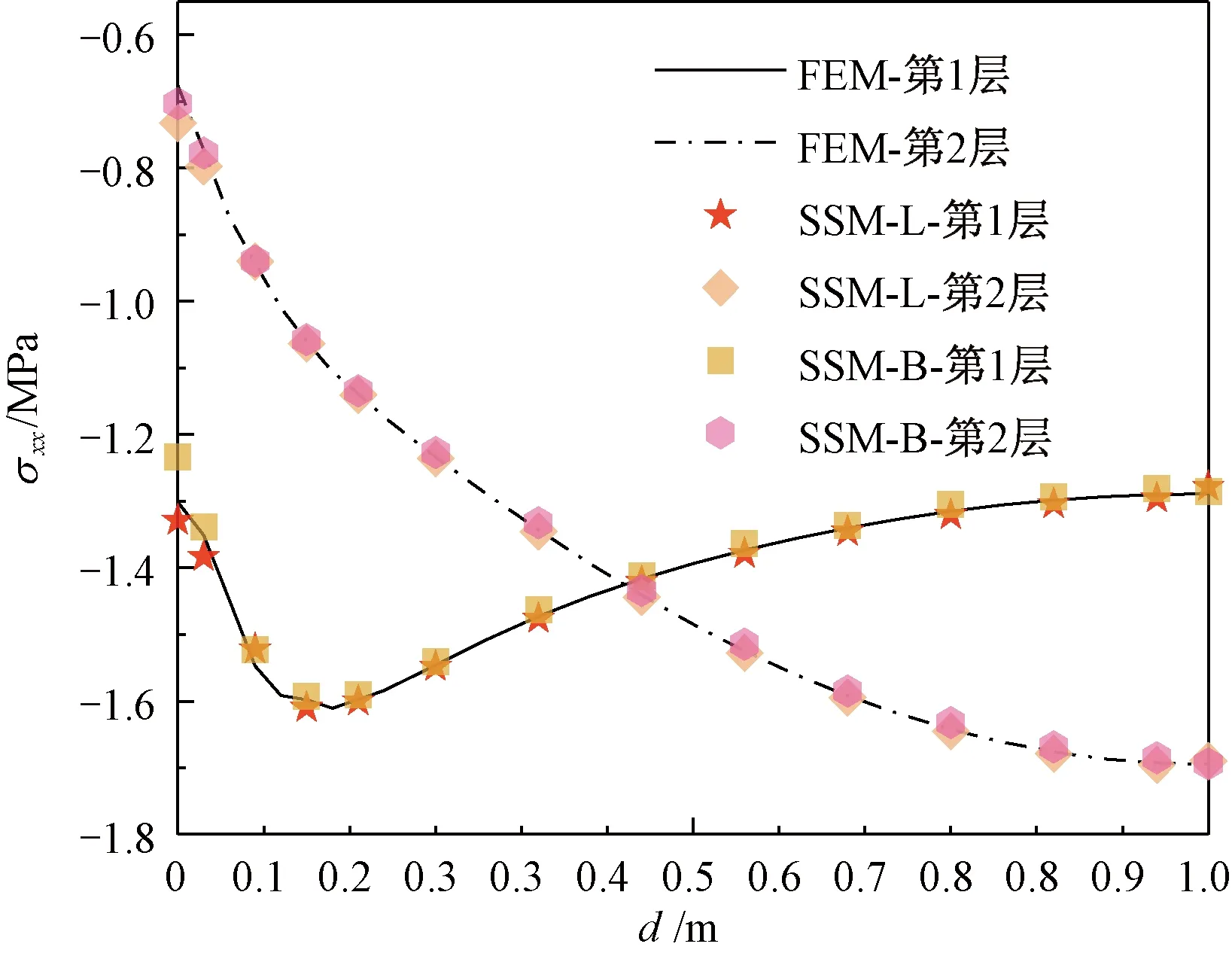
图6 不同离散法下第1、2层交界面应力σxxFig.6 Stresses σxx on the interface of 1st and 2nd layer by different discretizations
由图6可知,第1、2层交界面处,不同层所受到的应力σxx确实是不同的,但总体仍是边界处的变化更为剧烈。由图5和6可知,Lagrange单元离散法与B样条单元离散法的计算结果均能很好吻合有限元法结果。
4 结 论
本文使用状态空间法计算温度应力问题,研究表明:
——相较于传统的有限元方法,状态空间法在划分单元较少的情况下仍然得到较为精确的结果;计算时即使划分很多子层,仍然保持较快的计算速度。
——使用不同离散法,得到的结果略有差异,在B样条单元离散法的控制节点数量和Lagrange单元离散法的节点数量一致的条件下,B样条单元离散法得到的应力结果更为精确。
——比较精细积分法和通解法的计算时长及精度发现,无论何种单元离散方案,精细积分解法均优于通解法,主要体现在计算时长更短且精度更高。虽然两种方法需要计算的矩阵维度、大小相同,但得到矩阵的过程中精细积分法不需要计算eNi(hi),节省了大量时间。
