经编间隔织物增强硅橡胶基复合材料压缩行为的数学模型

周子祥，陈 思

(内蒙古工业大学 轻工与纺织学院,内蒙古 呼和浩特 010080)

由于纺织材料具备特殊的比模量、低密度和便于二次开发功能等特性,近年来其被广泛地应用于产业用纺织品[1]。经编间隔织物(warp-knitted spacer fabric,WSF)是由间隔丝连接两个分开的织物层构成,形成独特的三维结构。与机织物、非织造布相比,WSF具有更强的抗压变形能力和压缩恢复性[2],因此,其在应用于垫用复合材料[3]方面具有更大的潜力。

目前已有学者[4-9]开展了关于经编间隔织物增强复合材料力学性能的研究。但在实际应用过程中发现,最核心的问题是如何通过建立理论模型来预测复合材料的力学性能。陈思等[10]以文克尔弹性地基梁模型为理论基础,结合复合材料中间隔丝的结构参数,推导了经编间隔织物增强聚氨酯泡沫复合材料在压缩状态下的应力-应变方程,结果表明,理论方程可以较好地表征复合材料的压缩过程。陈思等[11]研究发现,在外界压缩荷载的作用下,复合材料中的间隔丝为主要受力单元,其中聚氨酯泡沫对间隔丝提供了一定的侧壁支撑。缪旭红等[12]使用弹性元件和黏性元件并联组成的Kelvin模型,对间隔织物振动时的黏弹行为进行分析,研究发现,间隔织物在振动过程中会通过自身的形变传递振动,其中间隔丝层则是主要的形变因素。陈美玉等[13]从理论上分析了压缩过程中经编间隔织物的缓压性能和其结构参数之间的联系,并计算出了各自的理论回归方程,研究发现,间隔织物的缓压性能在不同压缩荷载的作用下产生的变化趋势基本相同。文献[14-15]对经编间隔织物进行数学建模并设计试验,从实际和理论结合的角度分析了影响经编间隔织物负泊松比性能的因素。上述研究表明,理论模型可以有效地表征复合材料的受力演化过程,因此,理论模型的研究对复合材料的最优化设计具有重要的指导作用。

目前,经编间隔织物增强硅橡胶基复合材料(silicone-rubber-matrix composite reinforced by warp-knitted spacer fabric,SWSF)的力学性能研究尚处于试验阶段[16-18],其相应的细观力学理论模型研究尚未见报道。因此,本文根据Euler-Bernoulli梁理论[19]和Spence不变量本构理论[20],从细观力学的角度推导了SWSF中各组分在压缩荷载作用下的应力-应变本构方程,建立了包含SWSF各组分几何参数和性能参数的SWSF压缩细观力学理论模型。最后,将SWSF的压缩细观力学理论模型的计算结果和SWSF样品的压缩试验结果进行对比,以验证SWSF压缩细观力学理论模型的可靠性。

1 复合材料的制备

本研究选用的WSF由直径为0.16 mm的PET间隔单丝组成,其表层的网格单元为六角形网格。WSF的参数如表1所示。

表1 WSF的参数Table 1 The parameters of WSF

SWSF生产流程图如图1所示。由图1可知,由硅橡胶A和硅橡胶B按1∶1的质量比例,在室温下充分混合后制成硅橡胶基体。将WSF和硅橡胶基体完全混合,在室温下硫化静置8 h后,再将其置于室温下静置24 h,形成了本文的SWSF试样。SWSF试样的参数如表2所示。

图1 SWSF生产流程图Fig.1 The production flow chart for SWSF

表2 SWSF的参数Table 2 The parameters of SWSF

2 试验过程

根据GB/T 24442.1—2009《纺织品 压缩性能的测定 第1部分:恒定法》,在温度为18～22 ℃和相对湿度为55%～65%的环境下,将WSF和SWSF试样的底部平放在SHIMADZU万能试验机上,以速度为4 mm/min的匀速压缩荷载对试样的压缩性能进行测试,每种试样测试10组,结果求平均值。根据GB/T 528—2009《硫化橡胶或热塑性橡胶 拉伸应力应变性能测定》,在温度为18～22 ℃和相对湿度为55%～65%的环境下,使用SHIMADZU万能试验机中的上下两个夹具对硅橡胶材料进行夹持,将底部的夹具完全固定后,以速度为450 mm/min的匀速拉伸荷载对硅橡胶的拉伸性能进行测试。根据上述测试结果拟合了压缩细观力学理论模型中的系数C10和C01。

根据GB/T 8168—2008《包装用缓冲材料静态压缩试验方法》,同样在温度为18～22 ℃和相对湿度为55%～65%的环境下,将SWSF的底部平放在SHIMADZU万能试验机上,以速度为9 mm/min的匀速压缩荷载对其压缩性能进行测试。WSF和SWSF的压缩试验测试结果如图2所示。

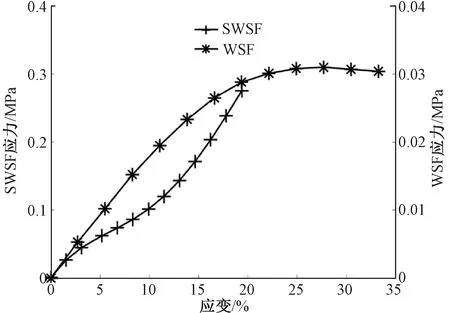
图2 WSF和SWSF压缩试验的测试结果Fig.2 The results of compressive experiment for WSF and SWSF

根据图2测试结果对压缩细观力学理论模型的准确度进行验证。从测试结果中筛选出13个具有代表性的试验点,绘制压缩测试的应力-应变曲线。压缩试验的平均标准差如表3所示。

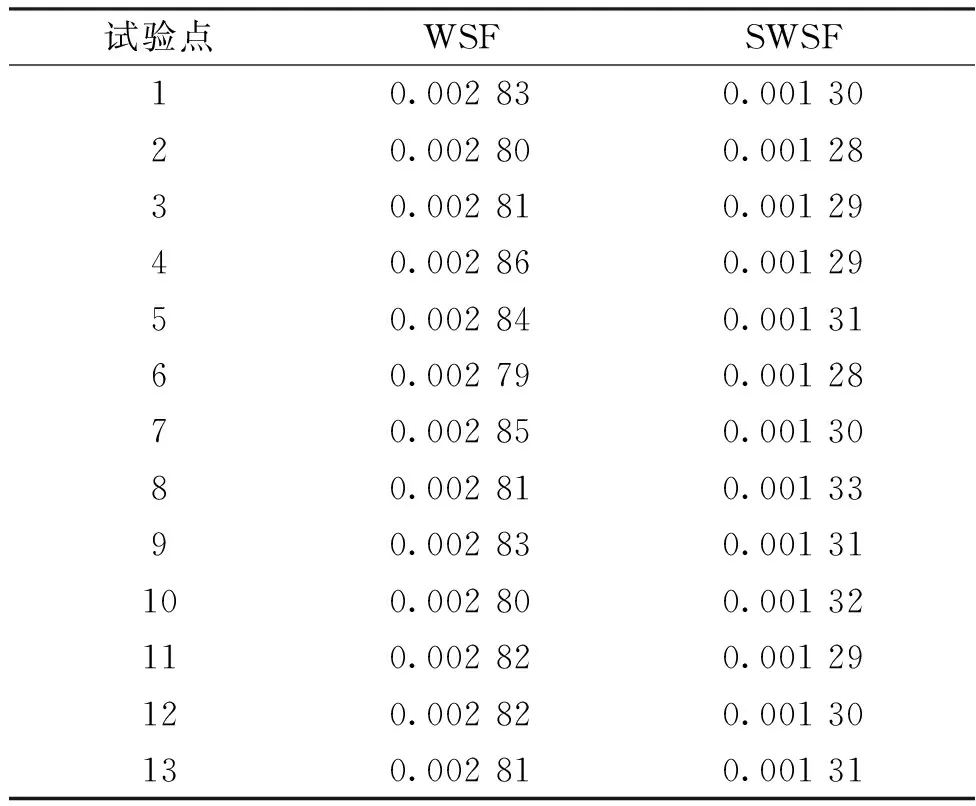
表3 试样压缩试验的平均标准差

由图2可知,SWSF承受的压缩荷载远大于WSF承受的压缩荷载,且SWSF的模量远大于WSF的模量,并在20%的应变点展现了良好的压缩潜能。另外,由表3可知,每组压缩试验的平均标准差较小且相近,说明取平均后的每组数据点都具有代表性。

3 模型建立

本研究的基体材料硅橡胶具有较低的弹性模量,因此具备良好的变形能力。同时,硫化前硅橡胶具有热塑性材料的特征,可以很好地与间隔丝混合,并与间隔丝之间保持高度的协调变形,为间隔丝提供可调节的侧壁支撑。作为增强体结构材料的WSF包含了间隔丝和织物层。根据间隔丝与织物层之间的连接方法,将间隔丝视为固定铰链,且间隔单丝的直径相对较小,因此间隔丝与织物层接触产生的剪应力可以忽略。假设间隔丝的截面沿其轴向均为统一的圆形截面[21],则可以将间隔丝视为连续的均质单元。在压缩试验时,由于间隔丝的弹性模量较高,应力主要被间隔丝吸收,织物层有轻微的变形。因此,织物层和硅橡胶混合后的单元可以视为实体面板,SWSF可以当作单组纤维增强的复合材料。本研究将SWSF处理成底部完全固定的Euler-Bernoulli梁,分析了SWSF压缩过程中间隔丝的变形。在ABAQUS软件中根据间隔梳栉的运动轨迹建立了间隔丝的轴线,以半径为0.08 mm的圆作为间隔丝的横截面,使用扫掠的方式构造了间隔丝的几何模型,对WSF中的间隔丝、实体面板赋予相应的材料参数后,在间隔丝和WSF的实体面板的接触区域设置了摩擦因数为0.5的接触约束。对WSF代表体单元的底端添加完全固定的边界条件,即底端每一个节点在x、y、z轴方向上的平动和转动自由度均为0。在代表体单元顶端设置速度为9 mm/min的恒定压缩荷载,最后对WSF的压缩行为进行模拟。WSF有限元模型的代表体单元的压缩变形示意图如图3所示。

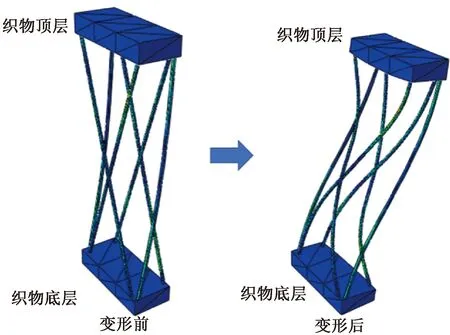
图3 WSF的压缩变形Fig.3 The compression deformation of WSF

根据WSF的压缩变形原理,假设未变形前的SWSF处于参考坐标系中,产生变形后的SWSF处于变形坐标系中。在参考坐标系中,间隔丝的初始方向为矢量场a0,其包含了XR的位置矢量X、间隔丝的长度为L0;在变形坐标系下间隔丝的方向为单位矢量场ai,其包含xi的位置矢量x、间隔丝长度为Li。拉伸比λ计算如式(1)所示。

λ=Li/L0

(1)

间隔丝的形变由式(2)～(4)所示。

x=x(X)

(2)

(3)

λai=gradDa0

(4)

式中:a0= (cosα,0,sinα),其中α为间隔丝与基体材料底部水平面的夹角,根据间隔丝的几何参数,可以计算出sinα=0.882,cosα=0.116;gradD为间隔丝的变形梯度,由间隔纱的局部旋转和间隔丝完整的压缩变形组成。

本文假设间隔丝在压缩过程中首先产生刚性压缩,然后被压缩体再进行旋转,继而对gradD进行了分解,如式(5)所示。

gradD=RU

(5)

式中:U为右变形张量;R为旋转矩阵。

在实际变形中旋转矩阵的计算需要消耗大量的计算成本,为了保证模型的计算精度并降低计算成本,假设复合材料在材料坐标系下产生形变,间隔丝的形变由式(6)代替。

gradDTgradD=(RU)TRU=UTRTRU=UT

U=U2=C

(6)

式中:C为右柯西-格林变形张量;U的特征值为λx、λy、λz(分别表示间隔丝沿x、y、z轴方向的拉伸比)。C的表达形式如式(7)所示。

(7)

最终,压缩过程中间隔丝的形变可以由式(8)确定。

λ2=a0gradDgradDTa0T=a0Ca0T

(8)

由式(8)可知,间隔丝的形变由向量a0和右柯西-格林变形张量C决定。由于SWSF可以看成是单组分纤维增强复合材料,本研究基于Spence不变量理论,使用不变量Ii(i=1,2,…,5)构建了SWSF的压缩细观力学理论模型。

(9)

(10)

(11)

I4=a0Ca0T

(12)

I5=a0C2a0T

(13)

SWSF在压缩过程中吸收的总应变能为W,如式(14)所示。

W=Ws+Wf=W(I1,I2,…,I5)

(14)

式中:Wf为增强体结构吸收的应变能;Ws为硅橡胶基体材料吸收的应变能,如式(15)所示。

Ws=W(C)=W(I1,I2,I3)

(15)

当材料为不可压缩体时,I3等于0,因此,硅橡胶基体材料吸收的应变能可以通过Mooney-Rivlin模型表达,如式(16)所示。

W(C)=C10(I1-3)+C01(I2-3)

(16)

假设W(C)对张量C是连续可导的,则:

(17)

(18)

(19)

式中:I为单位张量。

第二Piola-Krichoff应力T如式(20)所示。第二Piola-Krichoff应力T和Cauchy应力σ之间的关系如式(21)所示。

(20)

σ=J-1gradTgradDT

(21)

式中:J为体积模量。将式(20)代入式(21)计算得:

(22)

式中:W1、W2为不变量的偏导数;B为左格林-柯西变形张量。

σs=2[C10(λ2-λ-1)+C01(λ-λ-2)]

(23)

增强体结构吸收的应变能Wf,如式(24)所示。

Wf=W(C,a0⊗a0T)=W(I4,I5)

(24)

由于Wf和间隔丝的形变程度有关系,本文使用(I4-1)和(I5-1)的多项式构建了增强体材料吸收的应变能函数。

Wf=A1(I4-1)+A2(I4-1)2+A3(I5-1)+

A4(I5-1)2+A5(I4-1)3

(25)

假设Wf对张量C是连续可导的,则:

(26)

(27)

(28)

将式(26)～(28)代入式(21)中,并输入间隔丝的几何参数,最终得到了增强体材料的应力-应变关系,如式(29)所示。

σf=2A1(λ2-λ-1)+2A2[0.78(λ-λ-2)+

0.01(λ4-λ)+(λ-1-λ2)]+2A3[0.78(λ-λ-2)+

0.01(λ4-λ)]+4A4[0.61(λ-1-λ-4)+

0.01(λ2-λ-1)+0.02(λ3-1)]+3.54A5+

6A5(0.02λ3-0.61λ-3)+6A5(λ2-λ-1)+

12A5(-0.78λ+0.78λ-2)+12A5(-0.01λ4+λ)

(29)

4 结果与讨论

首先,在MATLAB软件的导入数据模块中导入硅橡胶力学试验数据。其次,在创建函数模块中输入硅橡胶基体材料的应力-应变本构方程,为区分硅橡胶基体材料应力-应变本构方程中的应力和硅橡胶基体材料试验数据中的应力,将式(23)中的σs替换为硅橡胶基体材料应力-应变本构方程中的应力数值。最后,在命令行窗口中输入非线性函数拟合指令,对硅橡胶基体材料应力-应变本构方程中的参数C10和C01进行计算。MATLAB软件的计算过程如图4所示。

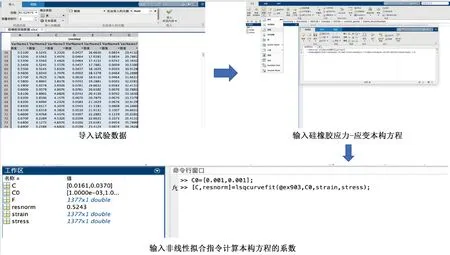
图4 MATLAB软件计算流程图Fig.4 Calculation flow diagram of MATLAB software

图4中,F为硅橡胶基体材料应力-应变本构方程中的应力数值,且非线性函数拟合的计算结果在工作区中显示,C为由C10和C01组成的矩阵,C0为可以任意设置的初始解向量,resnorm为拟合计算的残差平方和,strain和stress分别为硅橡胶力学试验的应变和应力数据。在导入数据时需要分析数据的可用性,排除由于机械误差等因素对试验结果真实性造成影响的数据,挑选可以体现材料属性的数据。同理,增强体材料应变能方程中的参数Ai(i=1,2,…,5)可以根据WSF的压缩试验结果得到,最终SWSF的应力-应变本构方程中的系数的计算结果如表4所示。

表4 理论模型参数Table 4 Theoretical model parameters

为了更加全面地分析SWSF的压缩行为,在MATLAB软件中对压缩试验结果进行了多项式曲线拟合,同时,将复合材料压缩试验的应变数据代入理论模型函数,最终对理论模型函数、多项式函数和试验结果3个曲线进行对比。SWSF的压缩曲线图如图5所示。

图5 SWSF的压缩曲线图Fig.5 Compression curves of SWSF

由图5可知,多项式拟合曲线主要分布在试验数据曲线的上方,理论模型曲线与试验结果曲线之间接触点的分布更均匀。多项式拟合数据与试验数据之间的平均相对误差为5.75%,其最大相对误差为16.11%。压缩细观力学理论模型计算数据与试验数据之间的平均相对误差为4.95%,其最大相对误差为11.20%。虽然3种压缩曲线之间仍存在一些偏差,但压缩细观力学理论模型可以有效地模拟SWSF在20%形变内的压缩演化过程。压缩曲线间的偏差原因:在压缩演化过程中,假设增强体与基体材料之间不存在剪切力,同时,复合材料只承受压缩载荷,忽略了间隔丝与硅橡胶之间的摩擦;在测量结构参数时,因人工操作而产生一定的测量误差;在计算过程中,间隔丝被视为直杆来计算夹角,但间隔丝并非是完全直杆,从而影响了夹角的精确度。在实际压缩过程中,上述原因的耦合作用产生了理论模型与试验结果之间的偏差。为了进一步理解本文方程对SWSF在20%形变内压缩过程的表征效果,对多项式方程和本文方程在各个应变点上的斜率进行了计算,并与试验数据在各个应变点上的弹性模量进行比较,方程斜率和SWSF的弹性模量如表5所示。

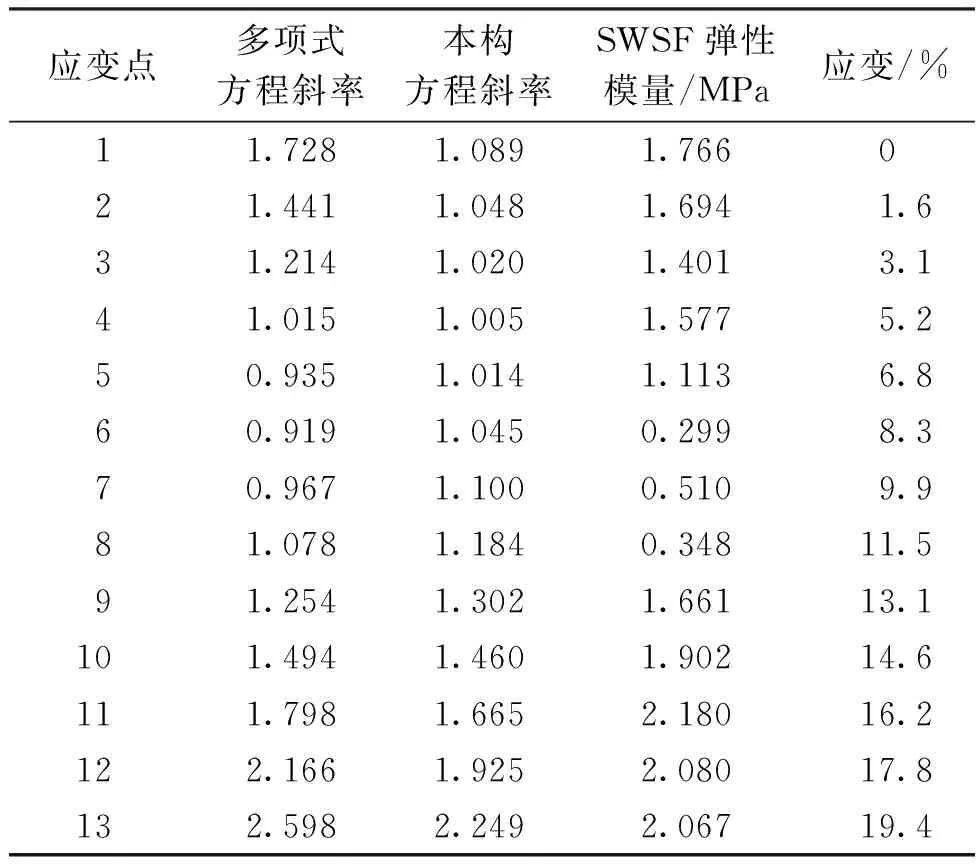
表5 方程斜率和SWSF的弹性模量Table 5 The slope of equation and elastic modulus of SWSF

由表5可知:当应变从0～11.5%时,多项式拟合和SWSF弹性模量之间的相对误差比本构方程和SWSF弹性模量之间的相对误差小20.681%;当应变为11.5%～20.0%时,本构方程和SWSF弹性模量之间的相对误差要比多项式拟合和SWSF弹性模量之间的相对误差小1.714%,本构方程和试验数据之间的平均相对误差为12.623%。通过上述分析发现压缩细观力学理论模型对SWSF的压缩行为分析具有一定的可靠度,因此,可以根据不同压缩状态的需求选择不同的方程斜率对SWSF的弹性模量进行参考设计,以达到设计要求。

5 结论与展望

本研究深入分析了经编间隔织物增强硅橡胶基复合材料 SWSF在外部压缩荷载作用下的受力机制,为其最优化设计提供了一定的理论基础,具体得出了如下结论:

——基于Euler-Bernoulli梁理论和Spence不变量本构理论建立的压缩细观力学理论模型,可以有效地模拟SWSF在20%变形内的压缩演化过程。

——当应变为11.5%～20.0%时,SWSF各阶段的压缩弹性模量可近似参考压缩细观力学理论模型曲线的斜率。

研究结果可为进一步研究SWSF的压缩特性提供参考,并有望扩展到预测不同结构SWSF的压缩特性。然而由于研究中模型的简化,压缩细观力学理论模型和压缩试验结果之间仍存在一定的偏差,压缩细观力学理论模型的斜率和SWSF的压缩弹性模量存在一定的离散,需要在后续的研究中进一步完善。