Simulation of DC glow discharge plasma with free-moving dust particles in the radial direction

Ruihuan TIAN(田瑞焕),Yonggan LIANG(梁勇敢),∗,Shuji HAO(郝书吉),Jie FENG(冯杰),Xiaonan JIANG(江晓楠),Hui LI(李辉),Chengxun YUAN(袁承勋) and Jian WU(吴健)

1 National Key Laboratory of Electromagnetic Environment(LEME),China Research Institute of Radio Wave Propagation,Qingdao 266170,People’s Republic of China

2 School of Physics,Harbin Institute of Technology,Harbin 150001,People’s Republic of China

Abstract A self-consistent fluid model is developed to investigate the radial distributions of dusty plasma parameters in a DC glow discharge,in which the extended fluid approach of plasma particles and the transport equations of dust particles are coupled.The electrical interaction between charged dust particles is considered in the model.The time evolution of radial distributions of dust density,plasma density,the radial component of electric field and the forces acting on dust particles when dust density tends to be stable,are obtained and analyzed under different discharge currents and dust particle radii.It is shown that the dust density structure is determined mainly by the radial electrostatic force,thermophoretic force and ion drag force in the discharge tube,and both discharge current and dust particle radius have an obvious effect on the transport processes of dust particles.The dust particles gather in the central region of the discharge tube for low discharge current and small dust radius,then dust voids are formed and become wider when the discharge current and dust radius increase.The plasma parameters in the dust gathering region are obviously affected by the dust particles due to the charging processes of electrons and ions to the dust surface.

Keywords: dusty plasma,glow discharge,extended fluid model,dust transport processes,dust-void

1.Introduction

Dusty plasma is a multicomponent plasma that includes electrons,ions,and additional species such as charged nanoto micrometer-sized dust particles or clusters [1].In recent decades,dusty plasmas have been paid more attention by many researchers because of their importance in many applications related to plasma,such as astrophysical topics[2-4],plasma materials processing [5,6] and fusion related research [7-9].In dusty plasma,ions and electrons are collected by dust particles,which leads to a change in the plasma properties.The dust parameters,such as dust density and dust radius,are critical factors in determining the effects of dust particles on plasma parameters,which should be confirmed before investigating dusty plasmas.

The influence of dust particles on plasma properties has been studied experimentally and theoretically by many researchers,and most of this research was carried out under two typical low-pressure discharge conditions,i.e.,DC glow discharge and RF discharge [10-17].Vasilyaket al[13]calculated the plasma parameters and electric field distribution in the radial direction in the positive column of air low-pressure glow discharge.In their model,the diffusion approximation was used to describe the plasma transport process,and it was assumed that the dust distribution was independent of the discharge conditions.Polyakovet al[14]studied,experimentally and theoretically,the changes in plasma parameters induced by clouds of disperse micron-size particles in the positive column of a low pressure and low current glow discharge.The numerical model consisted of the diffusion approximation and the orbital motion limited(OML) theory.The simulation result showed that dust particles brought the loss of free electrons and the increase in electric field,which was consistent with experimental results.Sukhininet al[15] presented a self-consistent kinetic model to describe the positive column in a DC glow discharge,where dust particles were introduced.The dust particle density distribution was set as a specific steplike function in their model.The interrelation of plasma property and dust particles was studied,and the radial distributions of plasma parameters and dust particle density were obtained in their study.

In most of the research about discharge dusty plasma,the dust particles have been assumed to be motionless and the dust densities are assumed to have a fixed flat spatial distribution,since the effects of dust particles on plasma properties can be obtained and analyzed easily with these assumptions.However,the dust particles that exist in plasmas,especially under gas discharge conditions in the laboratory,are subjected to many different forces,such as gravity,electric field force,thermophoretic force,ion drag force and neutral drag force etc.The dust particles in DC glow discharge hardly stay still.They will move and gradually form a particular structure under the action of these forces.One of the typical phenomena resulting from the dust transport processes is that a stable dust-void with a distinct boundary can be formed in the discharge tube [18-27].In order to study the spatial and time evolution processes of dust and plasma parameters in the discharge tube,it is necessary to consider the transport process of dust particles in the theorical simulation model of discharge dusty plasmas.

The work is devoted to the simulation of the dust and plasma characteristics in the radial direction in a DC glow discharge tube by considering the dust particle transport process.The simulation model is based on the extended fluid approach [28],in which the electron energy conservation equation is contained and the electron temperature can be calculated from the model instead of assuming it to be a constant.The continuity equation of plasma species and dust particles,the momentum equation of dust particles,the electron energy balance equation and the Poisson equation are considered in the model.The detailed model formulations are presented in detail in section 2.A 2D axial symmetry simulation model is built in this work,which means that the simulation conditions are closer to the actual experimental discharge conditions and the related simulation results should be more believable.The equations group of the simulation model is solved with help from the commercial software COMSOL Multiphysics,and the time evolution of dust density and the stable radial distributions of plasma parameters are obtained and analyzed in section 3.The conclusion is presented in section 4.

2.Model formulation

This work aims to study the spatial and time evolution processes of dust and plasma parameters in the radial direction of a DC glow discharge tube.In the discharge tube,the dust particles move and gradually form a particular structure under the action of various forces,and the plasma parameters change with the change in dust density distributions.The dust particles will stop moving until they reach the force balance region,where the radial distributions of dust and plasma parameters tend to be stable.A self-consistent theoretical model describing the plasma parameters and dust transport processes is developed based on the extended fluid model presented in [28].The continuity equation and momentum equation of dust particles are included in the simulation model to describe the temporal evolutions of dust particles selfconsistently.The motion of dust particles is dominated by the forces acting on them,such as electric field force,ion drag force,thermophoretic force and neutral molecule drag force.The model formulation is presented in detail as follows.

2.1.Charge number of dust particles

The dust particle charging process plays an important role in discharge dusty plasmas,since it is directly related to the electron and ion loss rates on the surface of dust particles and the charge number of dust particles.The most common method used to describe the dust particle charging process for collisionless dusty plasmas is the OML theory[29].While the plasma mentioned in this paper belongs to the weakly ionized and weakly collisional plasma,in which the ion-neutral collisions have a significant effect on the ion flux reaching the surface of dust particles,and the collision enhanced collection(CEC) approximation [30] should be employed to calculate the charging current of ions.Assuming that the electron and ion velocities meet the Maxwell distribution,the charging current of electrons and ions can be described as

wherene,Te,andmerepresent the density,temperature,and mass of electrons,respectively;ni,Tiandmirepresent the density,temperature,and mass of ions,respectively;kBis the Boltzmann constant;estands for elementary charge;rdand φdrepresent the radius and surface potential of dust particles;λis the Debye length; andliis the ion mean free path.

At the charging steady state,the balance equation of charging currents is

Substituting the electroneutrality condition(ni=ne+Ndzd) into equation(3),it can be obtained that

whereNdandzdare the density and charge number of dust particles,respectively.Cmeans the capacitance of dust particles,which is expressed asC=4πε0rd.The dust charge number is mainly determined by the plasma parameters generated in the discharge tube,and it can be calculated from equation(4) together with the system equations of the fluid model(described in the following section) for DC glow discharge dusty plasmas.

2.2.Forces acting on dust particles

In general,the forces acted on dust particles can be divided into two cases.One is the forces related to the charge of dust particles,such as the electrostatic force and the ion drag force.The other is the forces that are unrelated to the charge of dust particles,such as neutral molecular drag,gravity,and thermophoresis force.For the discharge conditions described in this paper,the discharge tube is vertically oriented to the ground.In this condition,the longitudinal thermophoretic force caused by the temperature gradient of the neutral gas(caused by the heating of the electrode) is along the axial direction.The gravity and longitudinal thermophoretic force are usually used to balance with the longitudinal electrostatic force(on the axial direction) to realize the levitation of dust particles in the vertically oriented discharge tube.Meanwhile,with the plasma parameters obtained in this paper,the calculation results of the radial thermophoretic force are comparable to the ion drag force.So,the radial thermophoretic force should be considered when simulating the plasma and dust parameters for the discharge conditions used in our paper.

With the limitations mentioned above,the total force on dust particles in the radial direction is expressed as

whereFE,Fid,FthandFndare the electric force,ion drag force,thermophoretic force and neutral molecular drag force in the radial direction.Specifically,the electrostatic force is expressed as

whereEris the radial electric field.As is the case for electrons,the electrostatic force stops the negatively charged dust particles from moving towards the discharge tube wall.Based on the two-body collision model,the ion drag force can be calculated from the formula [31]

whereυi=|υi|,υiis ion velocity,fi(υi) is the ion velocity distribution function,andare momentum transfer cross sections of ion collection and Coulomb scattering.For low-temperature plasmas,the ion velocity distribution function is usually assumed as [31]fi(υi)≈fi0(υi)(1+uiυi/uiT2),then the ion drag force can be deduced as

whereΠ is the modified Coulomb logarithm

The radial thermophoretic force can be approximately estimated by the formula [32]

whereris the radial coordinate,pis gas pressure,lgis the gas molecular free path,Tgis gas temperature,Iis the discharge current,Ezis the longitudinal electric field,ηis the thermal conductivity coefficient of gas,J0(r/Λ)is the Bessel function,Λ=Rtube/2.4,Rtubeis the radius of discharge tube andTwis the wall temperature.

For the dust particles moving in plasma,the friction on dust particles is mainly caused by their collisions with neutral molecular.The neutral molecular drag force is written as [33]

whereudrepresents the dust particle velocity andunrepresents directional macroscopic velocity(not the thermal velocity) of the neutrals.In DC glow discharge dusty plasmas,the velocity of neutral molecules is usually so small as to be negligible.νdnis the momentum transfer cross sections of dust and neutral gas,which is expressed as [34]

wherenn,mnandrnrepresent the density,molecular mass and molecular radius of the neutral gas,respectively.

2.3.System equations for DC glow discharge dusty plasmas

A self-consistent extended fluid model to describe the influence of dust particles on plasma parameters is presented in[35],in which the energy conservation equation is considered and the spatial distribution of dust particles is given as a fixed step function.Based on the extended fluid approach of discharge dusty plasmas,and considering the continuity and momentum equations of dust component as an additionalsupplement instead of assuming a fixed spatial distribution of dust particles,the system equations for DC glow discharge plasmas introducing radially free-moving dust particles are expressed in detail as follows.

For plasma parameters of discharge,the electron/ion continuity equation is expressed as

wherekrepresents species of plasma particles,nkis the number density;Skis source term caused by the plasma chemical processes;is the loss rate of electrons and ions on dust particles.Γkis the flux density;μkandDkrepresent the mobility and diffusion coefficient;E is the electric field;zkis the charge of electron/ion.

The electron energy balance equation is written as

wherenεis the electron energy density; Γεis heat flux density,which is described in detail in[36];andrepresent the energy change of electrons owing to the elastic and inelastic electron-neutral collision.

The electric field is obtained from the modified Poisson’s equation

whereε0is the vacuum dielectric constant;ndis dust density.

For the dust component,the governing equations are expressed as

where Γdis the flux density of dust particles;Tdis the thermal temperature of dust particles.

The radial distributions of dusty plasma parameters in DC glow discharge can be obtained by coupling the extend fluid model(equations(14)-(18)) and dust transport model(equations(19) and(20)).

3.Results and discussion

The 2D axial symmetry simulation model is established with the plasma module of COMSOL Multiphysics software,in which the finite-element method is used to solve various systems of partial differential equations.Figure 1 shows the schematic diagram of the discharge tube.The discharge tube is vertically oriented to the ground,and the dust particles with an initial radial density profile of the blurred step function are placed in the positive column of the discharge,where the plasma parameters are relatively stable and the axial inhomogeneity of the plasma parameters is much smaller than the radial ones.The axial size of the dust region is 2 cm.With proper dust parameters,the dust particles can levitate in the positive column under the action of gravity,thermophoretic force and axial electrostatic force for different discharge currents.Some of the experimental observation results of the levitation of dust particles under discharge current ranging from a few mA to a dozen mA are observed in [22,37].The argon discharge pressure is 0.2 Torr,and for argon discharge studied in this work,the plasma components are reduced to four species: neutrals(Ar),electrons(e-),ions(Ar+) and metastable atoms(Ar∗) with excitation energy of 11.72 eV.The plasma chemical processes of these species are described in detail in [35].

Figure 1.Schematic diagram of the discharge tube.

In our study,although the simulation model is a 2D axial symmetry simulation model,we only study the radial distributions of dust and plasma parameters for simplicity.The dust particles are negatively charged in positive column region of the discharge tube,so they are pushed to the tube wall by the ion drag forceFidand thermophoretic forceFthin the radial direction,meanwhile,the dust particles are captured at the discharge tube center by the radial electrostatic forceFE.The simulation is conducted under different discharge currents and dust parameters,since the ion drag force and electrostatic force acting on dust particles are dominated by them.It should be noted that different initial dust densities are employed for different discharge conditions and dust parameters to avoid the flameout of discharge caused by high density dust particles.The radial distribution of the concentration of dust particles will change due to the movement of dust particles until the total force on dust particles becomes close to zero,and the total number of dust particles in the discharge tube is constant.

Table 1.The discharge and dust parameters under different simulation conditions.

Specifically,the simulation conditions are presented in table 1.The discharge current in table 1 is defined as electron flux in the axial direction,which can be expressed as

whereSis the cross section of the discharge tube.

3.1.Simulation results for different discharge currents

The simulation results for different discharge currents shown in figures 2-5 are obtained with dust particle radiusrd=1μm.Figure 2(a)shows the evolution process of dust density radial distribution with discharge currentI=1 mA.It is shown that the dust particles gradually move towards the axis of the discharge tube and finally gather at the center region of the tube.The ion density and velocity are relatively small under small discharge current,which will lead to a small ion drag force and radial thermophoretic force.In this situation,the electrostatic force is always larger than the sum of ion drag force and thermophoretic force(see figure 5),which leads to a consistent movement of dust particles towards the discharge tube axis.Then the electric field near the tube center will be reduced due to the increase of density of dust particles with negative charge until the electrostatic force,ion drag force and the thermophoretic force can counteract each other.At that time,the dust particles will stop moving and sustain a stable radial density distribution.

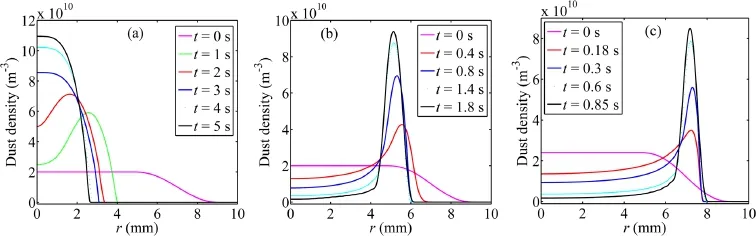
Figure 2.Evolution processes of dust density radial distributions with different discharge currents.(a) I=1 mA,(b) I=2 mA,(c) I=4 mA.

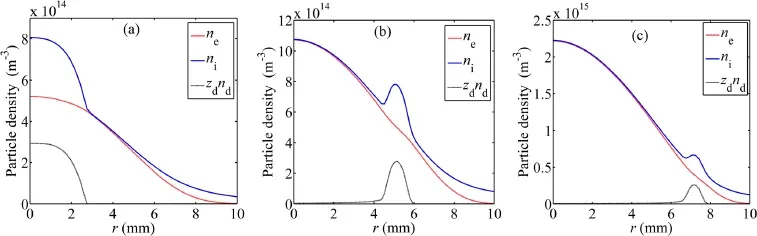
Figure 3.Radial distributions of charge density of electron,ion and dust particles when the dust distributions tend to be stable.(a)t=5 s and I=1 mA,(b) t=1.8 s and I=2 mA,(c) t=0.85 s and I=4 mA.

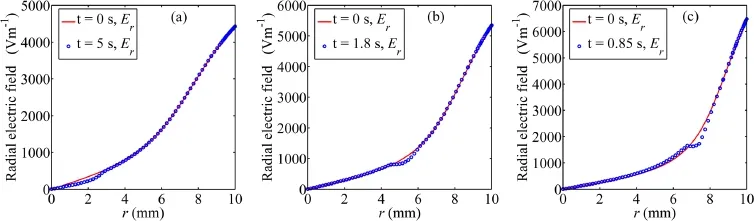
Figure 4.Radial component of electric field for different discharge currents when the discharge starts(t=0 s)and when the dust distribution tends to be stable.(a) I=1 mA,(b) I=2 mA,(c) I=4 mA.

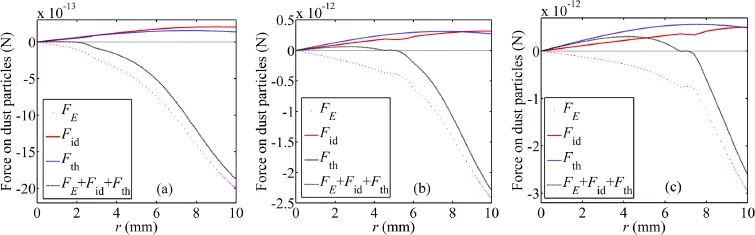
Figure 5.Distributions of radial force acting on dust particles when the dust distributions tend to be stable.(a) t=5 s and I=1 mA,(b)t=1.8 s and I=2 mA,(c) t=0.85 s and I=4 mA.

Figures 2(b) and(c) show the evolution process of dust density radial distribution with discharge currentI=2 mA andI=4 mA.It is shown that dust particles in both cases gradually move towards the tube wall and finally gather somewhere between the center and the tube wall.That is,a dust void is formed in the discharge tube,and this phenomenon has been confirmed experimentally by many researchers[19,22,23].When the discharge current increases,the ion density and ion velocity become lager,and,hence,the ion drag force becomes larger.It leads to a motion of dust particles towards the wall,and the dust gathering position is naturally farther away from the center for larger discharge current.It should be noted that the electrostatic force near the tube wall is very strong due to the existence of the plasma sheath,so the probability of dust particles reaching the tube wall is extremely small.

When the distribution of dust particles tends to be stable,the electron,ion,and dust charge density distributions in the radial direction under different discharge currents with dust particle radiusrd=1μm are shown in figure 3.It is shown that the electron density decreases slightly and the ion density increases obviously in the dust gathering region for all these three cases.In general,the electron density decreases quickly,firstly due to the charging processes after the dust particles are introduced.Then the electrons around the dust cloud diffuse into the dust cloud rapidly due to the large density gradient,and an ambipolar electric field is built immediately,which will push ions moving towards to dust region.This is the reason for the increase in ion density in the dust gathering region.The loss of electrons due to the collection process of dust particles can be made up by the diffusion process of surrounding electrons to a large extent,since the size of the dust gathering regions is sufficiently small.So,the electron densities only have a slight decrease in the dust gathering regions.

From figure 3,the minimum particle number densityndminleading to a ‘noticeable effect’ on the discharge plasma properties can be estimated.With the definition of a 10 percent change in ion density as the ‘noticeable effect’,the minimum particle number densitiesndminat the dust gathering region are calculated as about 1.8×1010m-3,1.75×1010m-3,1.3×1010m-3for different discharge currentsI=1 mA,2 mA and 4 mA,respectively.

The radial component of electric field when the discharge starts(t=0 s),and when the dust distribution tends to be stable for different discharge currents with dust particle radiusrd=1μm is shown in figure 4.It can be seen that,compared with the value at the initial time(t=0 s),the radial electric field in the dust gathering region becomes flatter,which is consistent with the calculation results from figure 2 in [25].With the increase of discharge current,the dust gathering region becomes closer to the tube wall and the influence of dust particles on the radial component of electric field becomes more obvious.For dusty plasmas,it is clear that the mobility and diffusion coefficients of dust particles,electrons and ions satisfy the relationμd≪μi≪μeandDd≪Di≪De,so the radial component of electric field can be estimated asEr≈-De∇rne/(μene).Then it is not hard to find that the radial component of electric field does not change much in the dust gathering region when the dust particles gather in the center region of the discharge tube,since the values of electron densityneand electron density gradient ∇rnedo not change much.With the increase in discharge current and dust radius,the dust gathering region becomes closer to the tube wall,and the influence of dust particles onneand ∇rnebecomes more obvious since the initial electron density decreases with the decreasing distance from the tube wall.So the influence of dust particles on the radial component of the electric field becomes more obvious accordingly.

When the radial distribution of dust density tends to be stable,the spatial distributions of forces acting on the dust particles under different discharge currents,with dust particle radiusrd=1μm,is shown in figure 5.The neutral drag force is absent in figure 5,because it takes the role of friction and is directly proportional to the dust velocity.When thedust distribution tends to be stable(i.e.,the dust velocity tends to be zero),the neutral drag force acting on dust particles will get close to zero too.It can be seen from figure 5 that the force balance region of dust particles varies with discharge currents.With the increase in discharge current,the force balance region gradually shifts towards the tube wall,since the increase of the sum of ion drag force and thermophoretic force is greater than that of electrostatic force when the discharge current increases.It should be noted that a local force balance region of dust particles instead of a force balance point is formed in the radial direction of the discharge tube.Because an ambipolar electric field is built around the dust region due to the ambipolar diffusion of electrons and ions,and the initial force balance point is extended widely by the ambipolar electric field.

3.2.Simulation results for different dust radii

The influence of dust radius on DC glow discharge dusty plasmas is discussed in this section.Figure 6 shows the evolution processes of dust density radial distribution with different dust radii and for discharge currentI=2 mA.It is shown that the dust particles gather at the center of the discharge tube forrd=0.5μm,and when the dust radius increases,the dust gathering region becomes farther away from the discharge tube axis.From equations(6)and(8),it is not hard to find that the relationship between electrostatic force and dust radius satisfiesFE∝zd∝rd,and the ion drag force and thermophoretic force satisfiesFid∝rd2andFth∝rd2,respectively.This means that the increase in the dust radius results in a larger increment of the ion drag force and thermophoretic force than that of electrostatic force.Therefore,the force balance region gradually shifts towards the tube wall with the increase in radius,which means that the dust gathering region becomes closer to the tube wall.

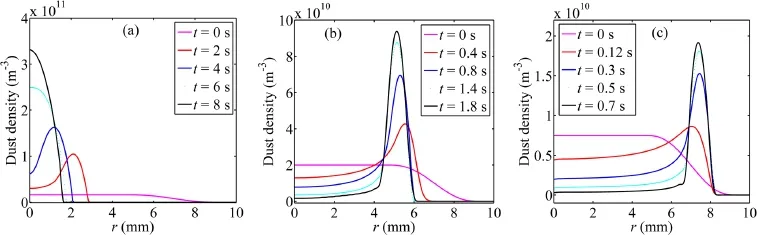
Figure 6.Evolution processes of dust density radial distributions with different dust radii.(a) rd=0.5 μm,(b) rd=1 μm,(c) rd=2 μm.

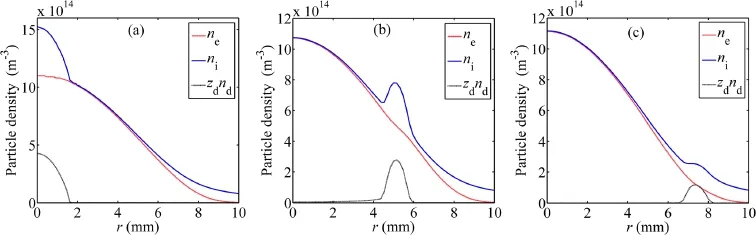
Figure 7.Radial distributions of charge density of electron,ion and dust particles when the dust distributions tend to be stable.(a) t=8 s and rd=0.5 μm,(b) t=1.8 s and rd=1 μm,(c) t=0.7 s and rd=2 μm.

Figure 8.Radial component of electric field for different dust radii when the discharge starts(t=0 s)and when the dust distribution tends to be stable.(a) rd=0.5 μm,(b) rd=1 μm,(c) rd=2 μm.

When the dust distributions tend to be stable,the charge density distributions of electrons,ions and dust particles in the radial direction for different dust radii and with discharge currentI=2 mA are shown in figure 7.The simulation results are similar to the results obtained for different discharge currents,i.e.,the electron density decreases slightly and the ion density increases obviously in the dust gathering region.Here,the minimum particle number densitiesndminthat lead to a ‘noticeable effect’ on ion density in the dust gathering region are calculated as about 8×1010m-3,1.75×1010m-3and 2.6×1010m-3for different dust radiird=0.5μm,rd=1μm,andrd=2μm,respectively.

The radial component of electric field when the discharge starts(t=0 s) and when the dust distribution tends to be stable for different dust radii with discharge currentI=2 mA is shown in figure 8.It is shown that,compared with the value at the initial time(t=0 s),the radial component of electric field does not change much in the dust gathering region when the dust particles gather in the center region of the discharge tube.With the increase in dust radius,the dust gathering region becomes closer to the tube wall and the influence of dust particles on the radial component of the electric field becomes more obvious,because the influence of dust particles onneand ∇rnebecomes more obvious in the dust gathering region closer to the tube wall.

Figure 9 shows the distributions of radial forces acting on dust particles for different dust radii and with discharge currentI=2 mA when the dust distributions tend to be stable.The neutral drag force is absent here too,since the dust distribution tends to be stable and the neutral drag force actingon dust particles gets close to zero.It is shown that a local force balance region of dust particles instead of a force balance point is formed due to the ambipolar electric field,and the force balance region gradually shifts towards the wall of the tube when the dust radius increases,since the increase in the dust radius leads to a larger increment of ion drag force and thermophoretic force than that of electrostatic force.

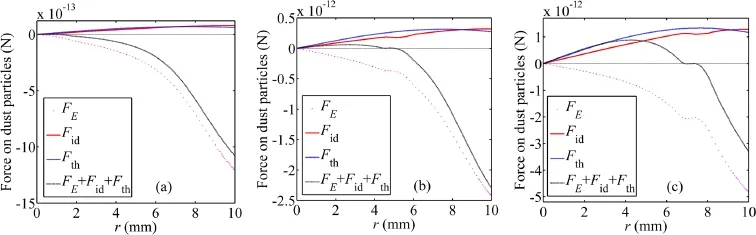
Figure 9.Distributions of radial forces acting on dust particles when the dust distributions tend to be stable.(a)t=8 s and rd=0.5 μm,(b)t=1.8 s and rd=1 μm,(c) t=0.7 s and rd=2 μm.

4.Conclusions

An extended fluid model for investigating the dust and plasma parameters generated in DC glow discharge is developed.The radial distributions of dust density,electron/ion density,the radial component of electric field and forces acting on dust particles are calculated numerically by coupling the dust chargingcurrents balance equation and the extended fluid model equations.The influences of discharge current and dust radius on these dusty plasma parameters are obtained and discussed.

According to the simulation results,it is concluded that both discharge current and dust radius have obvious influences on the dusty plasma parameters under DC glow discharge conditions.When the discharge current is low(I=1 mA)and dust radius is small(rd=0.5μm),the dust particles gradually move towards the center of the discharge tube and finally gather in the center region,since the electrostatic force acting on dust particles is always larger than the sum of ion drag force and thermophoretic force in the entire radial path.With the increase in discharge current and dust radius,the distance between the dust gathering region and the tube axis becomes larger due to the more obvious increase in ion drag force and thermophoretic force.The local force balance region of dust particles varies with the dust gathering region accordingly.The electron and ion densities are affected by the dust particles too.The electron density decreases slightly due to the fast diffusion of electrons and the ion density increases obviously due to the electroneutrality condition in the dust gathering region for all discharge conditions presented in this paper.The radial electric field in the dust gathering region becomes flatter compared with the value at the initial time,and the influence of dust particles on the radial component of electric field becomes more obvious with the increase in discharge current and dust radius,since initial electron density becomes smaller in the corresponding dust gathering region.Compared with the calculation results obtained under the assumption of fixed constant distributions of dust density,the simulation results obtained in this paper should be more realistic.

Acknowledgments

This research is financially supported by the Stable-Support Scientific Project of China Research Institute of Radiowave Propagation(No.132101W07),National Natural Science Foundation of China(No.12105251),and National Key Laboratory Foundation Electromagnetic Environment(Nos.A382101001,A382101002 and A152101731-C02).

ORCID iDs