基于VOF模型的真空吸鱼泵数值模拟

楚树坡,徐志强,张耀明,谭永明,林礼群,,王志勇,

(1.青岛海洋科技中心,山东 青岛 266237;2.农业农村部设施农业装备与信息化重点实验室,浙江 杭州 310058;3.中国水产科学研究院渔业机械仪器研究所,上海 200092)

鱼类的起捕与输送是渔业生产中的重要环节,吸鱼泵因具有自动化程度高、工作效率高、劳动强度低、操作人员少等优点,在鱼类的起捕与输送环节具有广阔的应用前景。吸鱼泵的研制始于20世纪50年代,最早应用于拖网和围网渔业活动中渔获的海上及港口转运、卸载操作等[1-2]。随着水产养殖业的发展,特别是随着大型深水网箱的推广应用,渔获量激增,传统的人工起鱼作业已无法满足要求,自动高效的吸鱼泵成为主要起捕工具[3-4]。在南极磷虾捕捞作业中,采用吸鱼泵的连续高效捕捞技术已成为国际上最先进、最高效的捕捞技术[5-7]。国际上普遍使用的吸鱼泵结构型式主要有3种,即离心式、真空式和射流式[8-9]。其中,真空吸鱼泵因无运动部件,结构简单,工作效率高,能耗较低,对鱼类无损伤,适合输送较大体型的活鱼等优点,成为国际上商业化应用最广的吸鱼泵[10]。

真空吸鱼泵由真空罐、水环真空泵、控制箱、阀门、仪表以及管道等组成。真空吸鱼泵的工作原理如下：水环真空泵将真空罐内空气抽出,真空罐内形成负压,鱼水混合物在真空罐内外压差的作用下,沿吸鱼管进入真空罐;达到排放条件后,在重力(或气压)的作用下,鱼水混合物从真空罐的排鱼口排出,从而完成一个吸/排鱼过程[11]。目前对真空吸鱼泵的研究多集中于真空吸鱼泵的设计计算、智能控制以及性能试验[12-19],其中真空吸鱼泵的设计计算主要依赖于工程经验,存在很大的随意性和不确定性等缺点,如果没有丰富的设计经验,设计的真空吸鱼泵很可能无法达到设计目标。国内外已有学者尝试通过数值模拟手段开展真空吸鱼泵研究,如田昌凤等[20]采用Volume of Fluid(VOF)模型研究了不同进鱼管道抽吸速度下的真空罐内流场分布情况,并基于数值模拟结果研制了小型单罐真空吸鱼泵;林礼群等[21]采用VOF模型研究了-30 kPa抽气压力下的真空罐内流场分布情况以及抽气压力对吸鱼管道进口和真空罐进口水流速度的影响。

真空吸鱼泵是通过水环真空泵对真空罐抽气进而吸鱼的,故本研究采用VOF模型,以抽气速度为边界条件,模拟真空吸鱼泵的吸/排水过程,获得过程中的速度、压力、相分布等流场信息,以及吸/排水时间信息,并对吸捕速率进行预测,以期对后续真空吸鱼泵结构优化以及系统工程设计提供理论参考。

1 数值模拟

1.1 物理模型

真空吸鱼泵的一个吸/排水过程包括吸水和排水2个阶段,本研究对吸水和排水阶段分别进行数值模拟。为了预测吸/排周期时长及真空吸鱼泵吸捕速率,设定吸水停止与排水开始2个时刻的真空罐中液相体积相等。真空吸鱼泵吸水和排水阶段的物理模型示意图见图1。

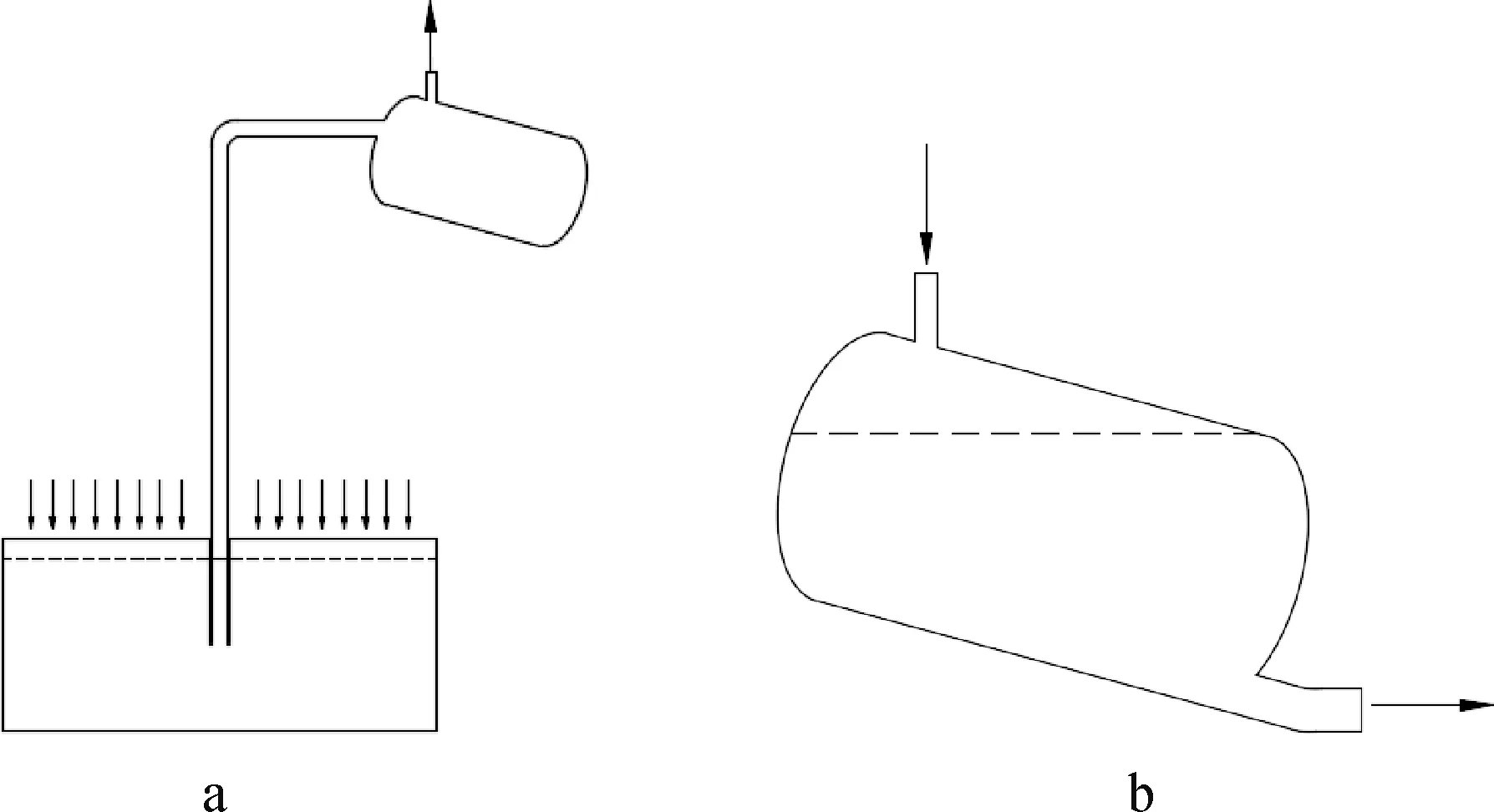
图1 吸水和排水阶段物理模型示意图注：a：吸水阶段;b：排水阶段。Fig.1 Sketch of physical model of the suction and discharge stageNotes：a：Suction stage;b：Discharge stage.

真空吸鱼泵吸水和排水阶段的物理模型均采用二维模型,真空罐直径为260 mm,直筒段长度为370 mm,两端为标准椭圆形封头(长轴与短轴之比为2),进水口直径为40 mm,出气口直径为20 mm,排水口直径为40 mm,排水开始时刻真空罐内液相体积为9 600 mm2。

1.2 控制方程

不考虑鱼类的影响,真空吸鱼泵吸/排水过程中只涉及水和空气两相,两相之间有着明确的界面,因此可采用多相流中的VOF模型进行数值模拟。VOF模型适用于分层的或自由表面流,是一种重要的运动界面追踪方法,由Hirt和Nichols在1981年所提出[22]。此模型定义一个随时间和位置变化的函数α,用来标识控制容积内目标流体的体积与网格体积的比值。当α= 1时,表明该控制容积内充满目标流体;当α=0时,表明该控制容积内充满另一种流体;当0<α<1时,表明该控制容积内包含相界面。

对于气液两相,气相设置为基本相,液相设置为第二相,本问题的控制方程如下[23-25]：

气相体积分数方程

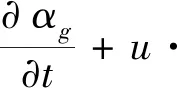
式(1)

式中,αg为气相体积分数;u为流体速度矢量,m/s;t为时间,s。

液相体积分数约束方程

αg+αl=1

式(2)

式中,αl为液相体积分数。

连续性方程为

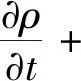
式(3)

式中,ρ为流体密度,kg/m3。

动量方程为

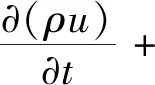
式(4)

式中,p为流体静压力,Pa;μ为流体动力黏度,kg/(m·s);g为重力加速度,m/s2;F为动量源项,N/m3。

流体的密度和动力黏度定义为：

ρ=αgρg+(1-αg)ρl

式(5)

μ=αgμg+(1-αg)μl

式(6)

式中,ρg、ρl分别为气相和液相的密度,kg/m3;μg、μl分别为气相和液相的动力黏度,kg/(m·s)。

应用CSF(Continuum Surface Tension)模型考虑表面张力的影响,将表面张力作为体积力加到动量方程源项中：

式(7)

式中,σ为表面张力系数;k为表面曲率,定义为单位法向量的散度。

式(8)

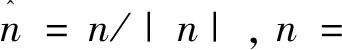
1.3 模拟方法

采用双精度求解器进行非稳态计算,湍流模型采用Realizable k-ε模型,多相流模型采用VOF模型。采用SIMPLEC格式的速度压力耦合方法进行速度场求解,气相体积分数方程采用显式时间步进格式,体积分数插值采用Geo-Reconstruct格式。为加速求解收敛,方程求解时采用NITA(Non-iterative time-advancement scheme)格式和隐式体积力(Implicit body force)处理方式,时间步大小设置为1×10-3s。

1.4 初始及边界条件

对于吸水阶段,边界条件设置如下：水池液面设置为“压力入口”,数值为0 Pa(相对压力,绝对压力则为101 325 Pa,下同);真空罐出气口设置为“速度进口”;真空罐及吸鱼管内壁均设置为无滑移壁面。初始时刻,水池液面以上的吸鱼管内部以及真空罐内部全部为气相,初始压力设定为0 Pa。

对于排水阶段,边界条件设置如下：真空罐进气口设置为“压力入口”,数值为0 Pa;真空罐出水口设置为“压力出口”,数值为0 Pa;真空罐内壁设置为无滑移壁面。初始时刻,真空罐内液相体积为9 600 mm2。

1.5 网格无关性验证

采用Gambit对计算域划分网格,网格采用四边形非结构网格。网格的质量和数量对模拟结果有着重要影响,在保证网格质量的前提下,验证网格数量对数值模拟结果的影响十分重要。通过对同一模型划分不同的网格数量进行数值模拟,通过比较数值模拟结果来验证网格无关性[26]。以排水阶段为例,选取4套网格进行数值模拟,以排水时间为参数,结果如图2所示。图2显示,当网格增加到128 704个时,继续增加网格数量,排水时间不再变化。综合考虑计算精度和时间成本,排水阶段最终采用网格数量为128 704个的模型进行模拟。吸水阶段亦如此进行网格无关性验证。

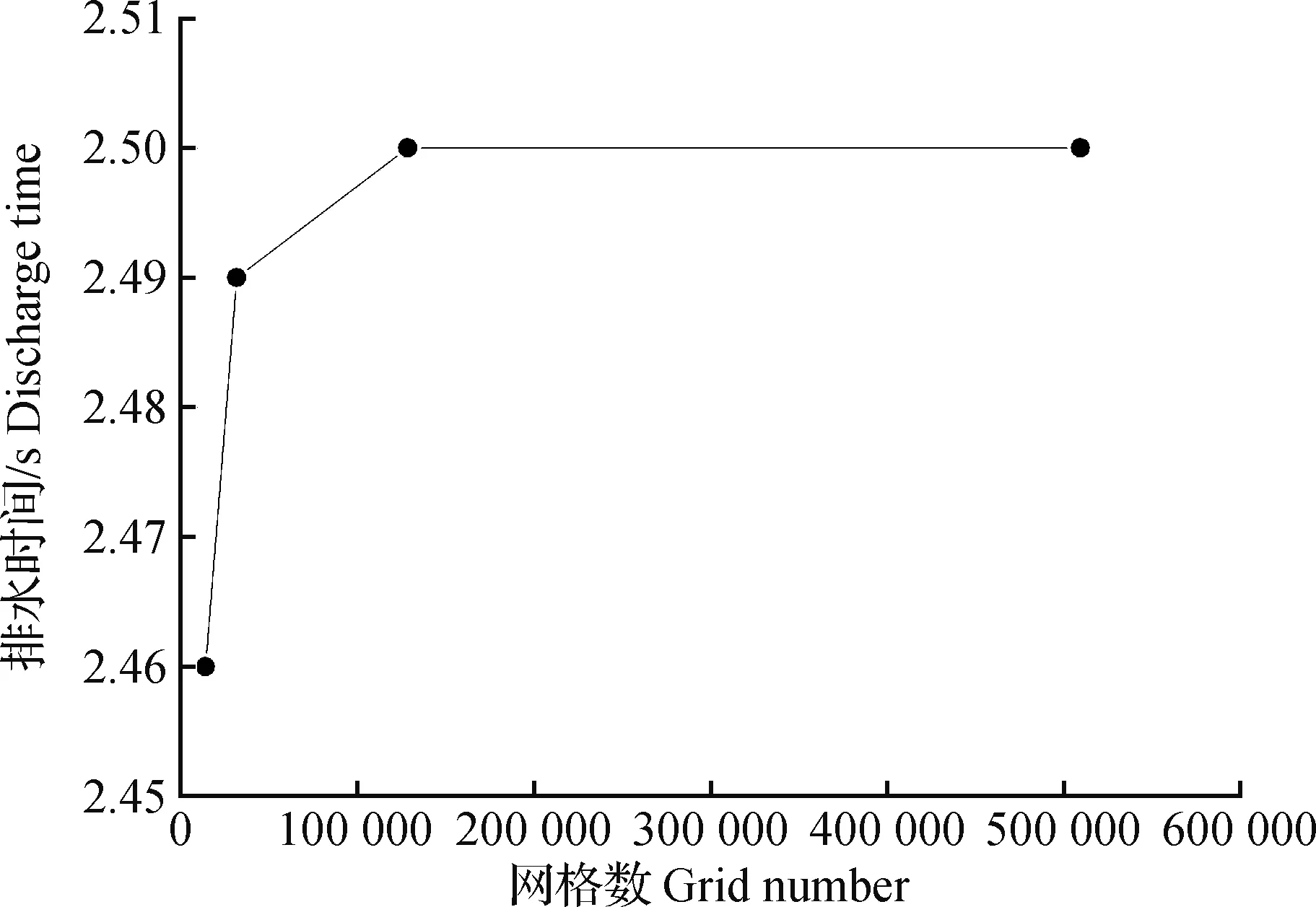
图2 网格无关性验证Fig.2 Grid independence verification

2 结果与分析

2.1 吸水阶段

随着对真空罐不断抽气的进行,真空罐内部压力降低,低于水池液面处压力(1个大气压,0 Pa),在水池液面处与真空罐内部压差的作用下,水从水池中进入吸水管道和真空罐内。吸程为1.0 m,抽气速度为1.5 m/s时,吸水阶段计算区域液相体积分数随时间变化的历程如图3所示。

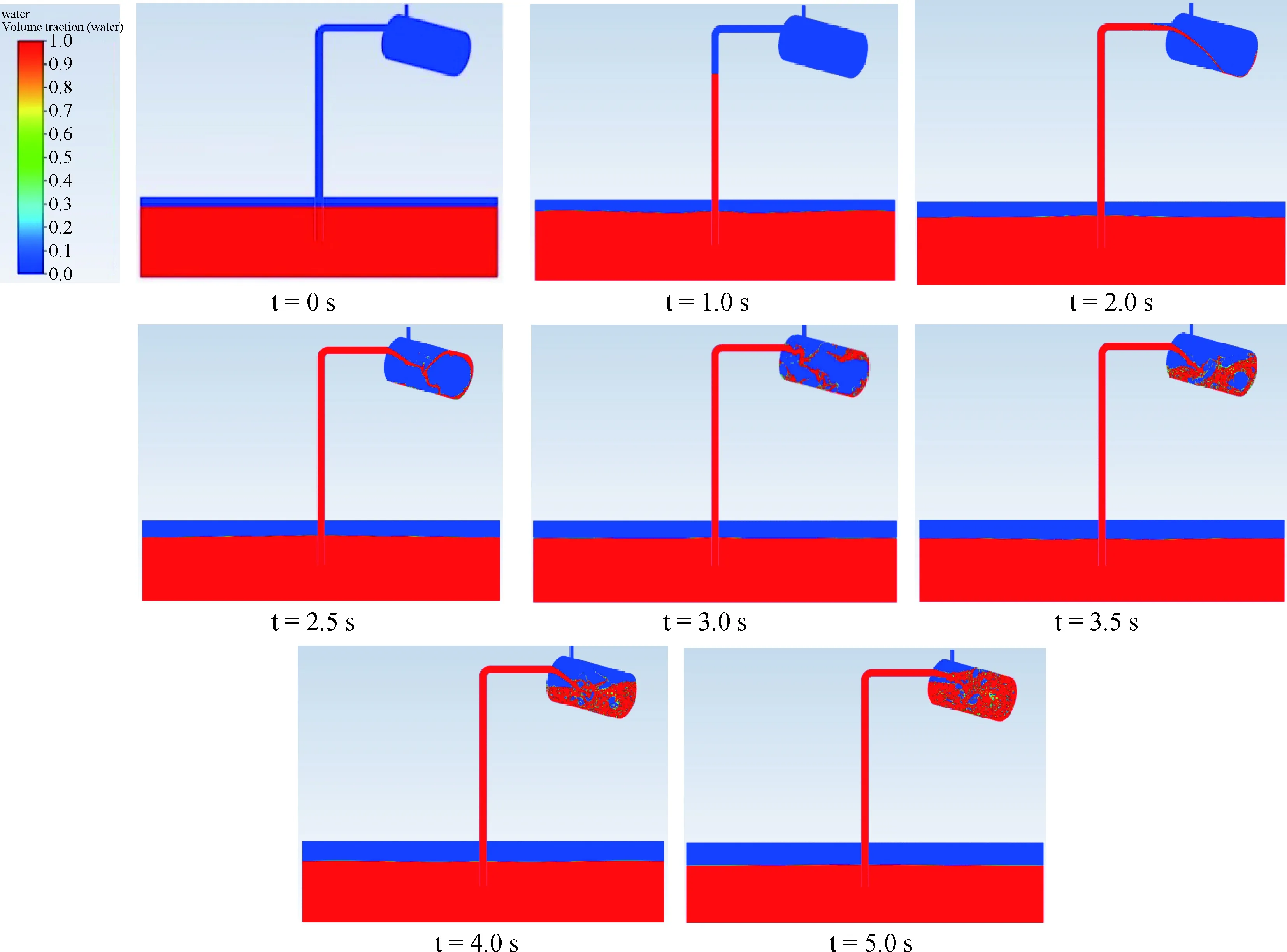
图3 吸水阶段液相体积分数演化(H=1.0 m,V=1.5 m/s)Fig.3 The evolution of liquid volume fraction during suction (H=1.0 m,V=1.5 m/s)

2.2 抽气速度相同而吸程不同时的吸水模拟

抽气速度相同(V=1.5 m/s)时,尽管吸程不同,但吸水管道内的流速是相等的(均为0.75 m/s),且吸水阶段几乎不变(图4)。

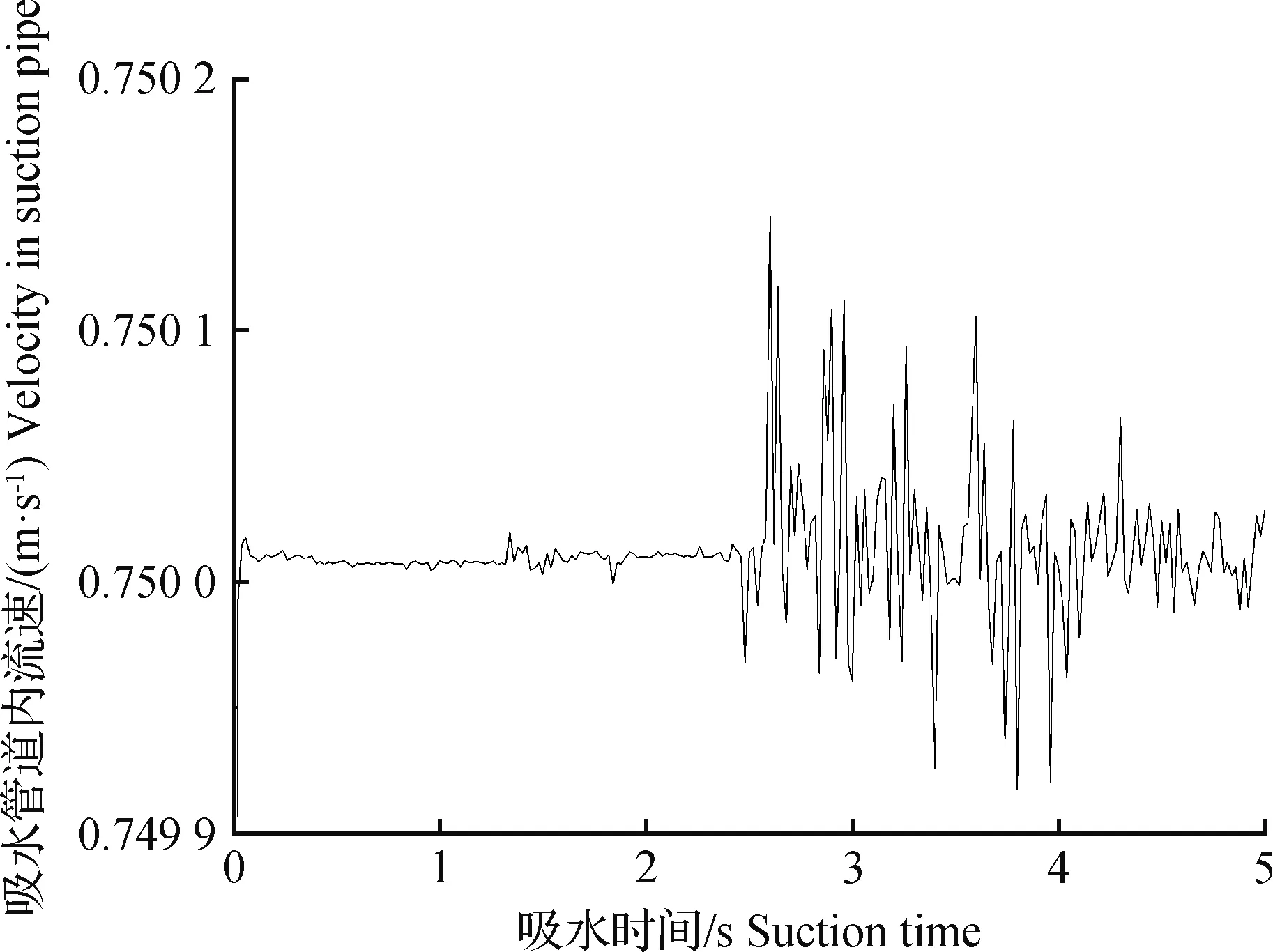
图4 吸水管道内流速变化曲线(H=1.0 m,V=1.5 m/s)Fig.4 Velocity-time curve in suction pipe (H=1.0 m,V=1.5 m/s)

吸水阶段又分为两个时段：吸水初期,随着吸水过程的进行,真空罐内压力快速降低,水池中的水沿着吸水管道上升,该时段为压力快速变化时段;当水上升至水平管道处后,真空罐内部的压力变为稳定,该时段为压力稳定时段(图5)。

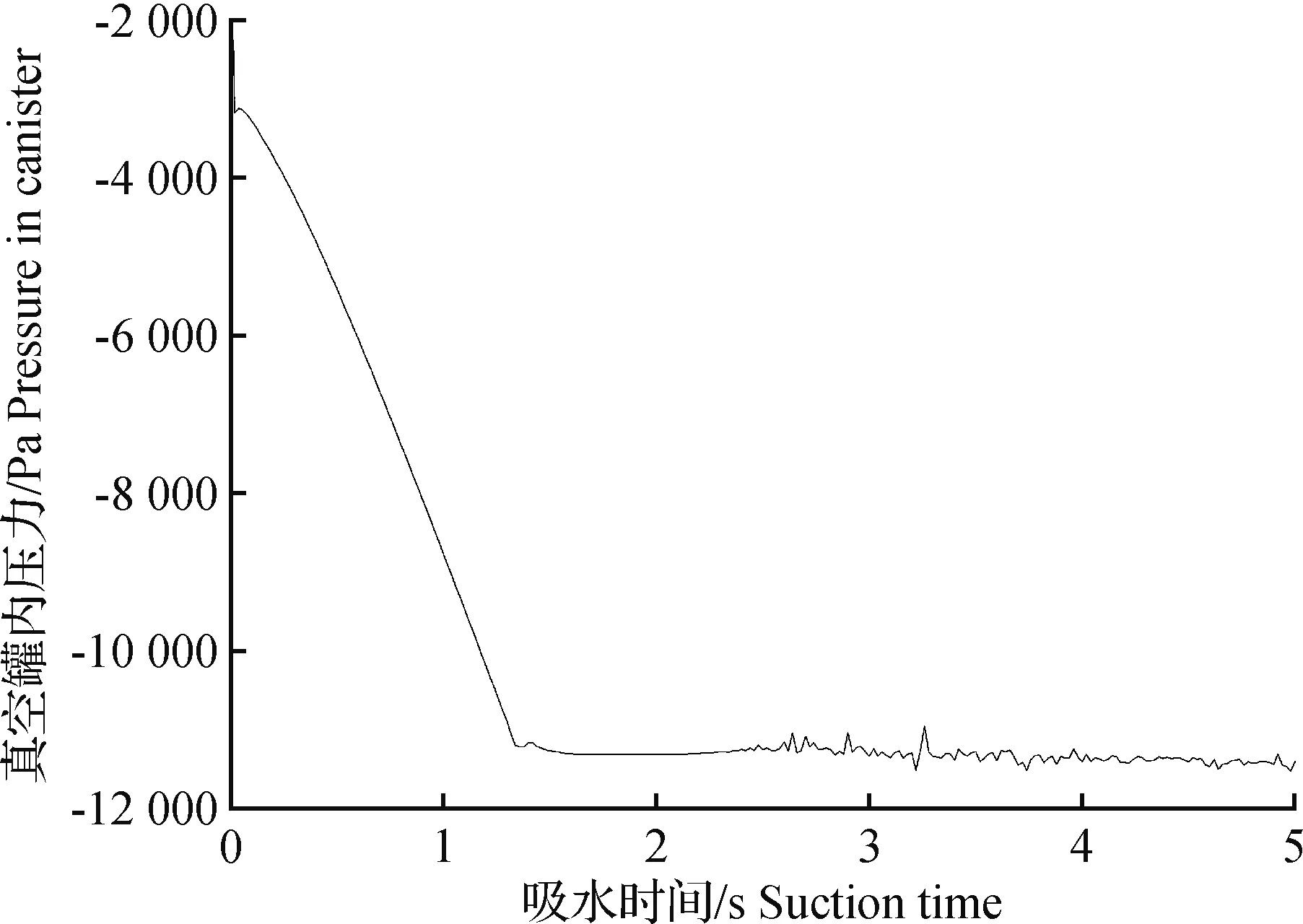
图5 真空罐内的压力变化曲线Fig.5 Pressure-time curve in canister (H=1.0 m,V=1.5 m/s)

在相同抽气速度条件下,为使真空罐内吸取相同体积(9 600 mm2)的水,随着吸程的增大,吸水时间逐渐增加,真空罐内稳定工作压力逐渐降低(图6),这与楚树坡等[19]研究中真空吸鱼泵吸水性能试验的结论一致。吸水时间的增加,主要是由于吸水管道长度增大。当吸程增大到一定程度后,真空罐内稳定工作压力很低,鱼类在被吸上的过程中,因鱼体内外压差较大,可导致鱼体内部损伤[27],因此应根据所吸鱼能够承受的体内外压差限定最大吸程。

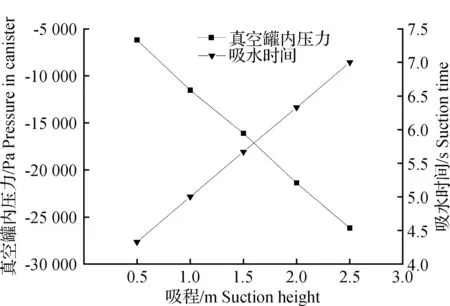
图6 真空罐内压力、吸水时间与吸程的关系Fig.6 Pressure in canister and suction time with different suction heights

2.3 吸程相同而抽气速度不同时的吸水模拟

吸程相同时,为使真空罐内吸取相同体积(9 600 mm2)的水,随着抽气速度的增大,吸水时间逐渐减少,真空罐内稳定工作压力逐渐降低,吸水管道内流速逐渐增加(图7)。

图7 真空罐内压力、吸水管道内流速与抽气速度的关系Fig.7 Pressure in canister and velocity in suction pipe with different extraction speeds

在真空吸鱼泵实际运行中发现,吸水管道内速度过大时,水流进入真空罐后,初期会剧烈撞击真空罐内壁,水流中若有鱼,则鱼会因撞击坚硬的真空罐内壁而损伤;随着真空罐内部水量增加,后期进入真空罐内部的高速水流会冲击已有水体,导致水体剧烈扰动,水流以及水体中若有鱼,则会导致鱼类之间相互摩擦而损伤。抽气速度为2.5 m/s时的数值模拟结果可以明显地看到真空罐内部出现了剧烈的水流扰动(图8)。尽管增大抽气速度会缩短吸水时间,提高吸捕速率,但若抽气速度过大,导致鱼类撞击真空罐内壁以及鱼类之间相互摩擦而损伤,反而得不偿失。再者,降低抽气速度,也会降低水环真空泵投资以及能耗,降低设备购置成本以及运营成本。因此,设计真空吸鱼泵时应控制抽气速度在适宜的范围内。

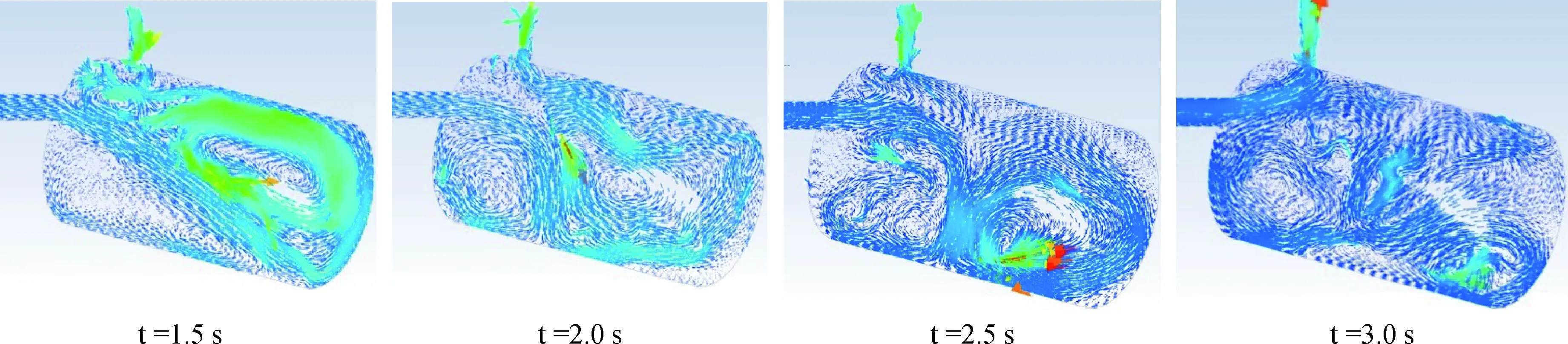
图8 真空罐内的速度矢量图(H=1.0 m,V=2.5 m/s)Fig.8 Velocity vector profile in canister (H=1.0 m,V=2.5 m/s)

2.4 排水阶段模拟

排水阶段,在重力(或加压)的作用下,真空罐内的水从排水口排出,水逐渐减少,直至全部排光。排水阶段计算区域液相体积分数随时间变化的历程见图9。

图9 排水阶段液相体积分数演化Fig.9 The evolution of liquid volume fraction during discharge

数值模拟结果显示,经过2.5 s即可将真空罐内9 600 mm2的水排完,排水阶段排水口处的速度随时间的变化曲线见图10。经计算,排水阶段排水口的平均流速为0.96 m/s。

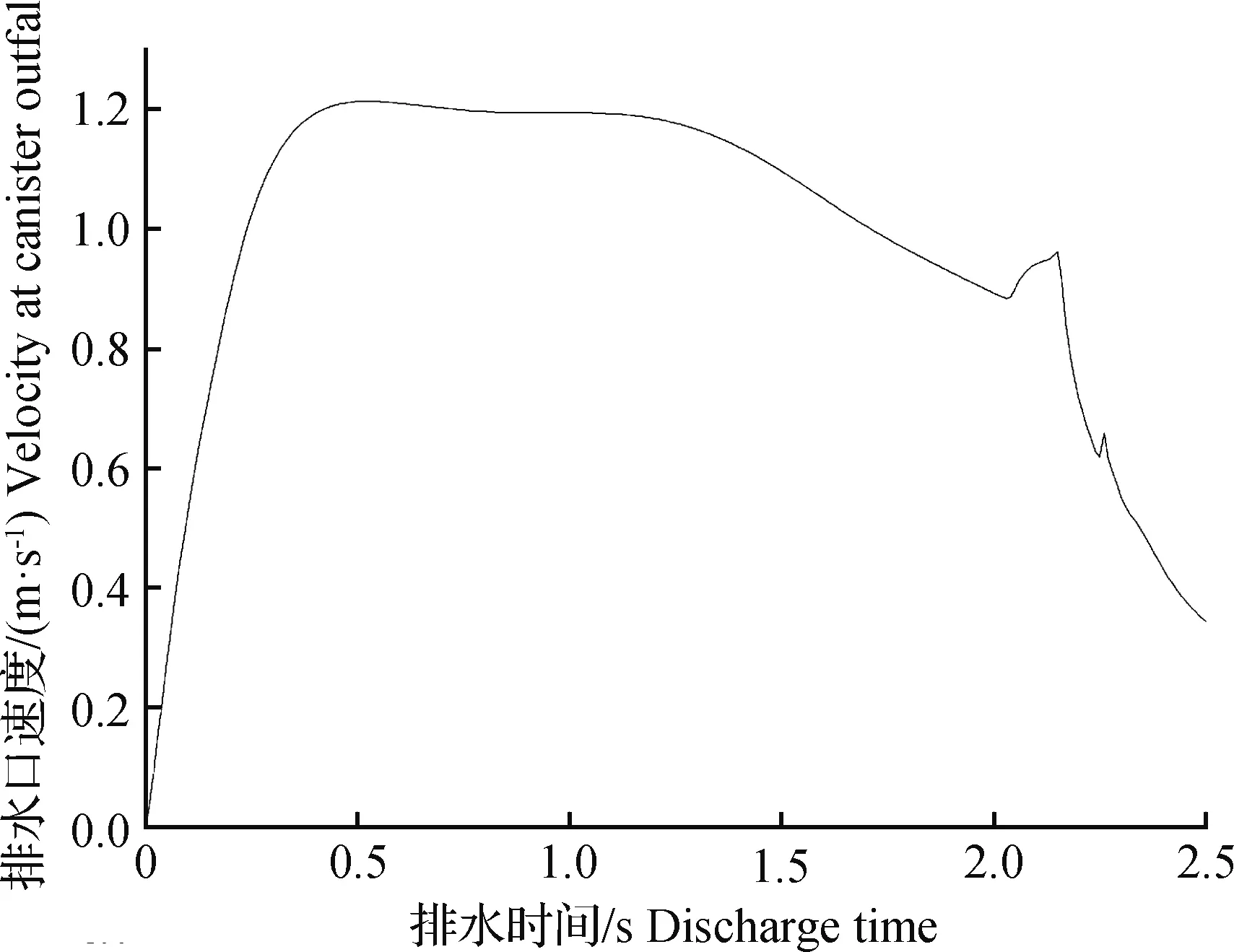
图10 真空罐排水口速度-时间曲线Fig.10 Velocity-time curve at canister outfall

3 讨论

设计某规格的真空吸鱼泵时,设计输入条件为吸捕速率、吸程、所吸鱼的生长参数以及所吸鱼的极限游速等数据。真空吸鱼泵的设计计算过程为：首先假定一个吸/排周期时长,通过计算确定单个吸/排周期内的吸水量,而后再确定真空罐的参数;抽气时间同时又是计算选定水环真空泵的一个重要参数,有了抽气时间、真空罐容积、真空罐内稳定工作压力等参数,通过计算确定水环真空泵的抽气速度,进而选择水环真空泵的规格型号[11-14]。从真空吸鱼泵的设计计算过程可以看出,计算的初始条件(吸/排周期时长)是假定的,而不是已知的,因而真空吸鱼泵的设计计算具有很大的随意性和不确定性;如果没有丰富的设计经验,设计很可能失败。通过数值模拟,可以得到准确的吸水时间、吸程、真空罐内压力、吸水管道内流速、抽气速度等的关系以及排水时间,根据此数值设计出来的与所需要的真空吸鱼泵更为接近,而且可以缩短开发时间,降低开发成本,因此数值模拟是设计真空吸鱼泵非常有效的手段。

根据本研究的数值模拟结果,真空吸鱼泵的设计参数如下：当吸程为1.0 m、抽气速度为1.5 m/s时,吸水时间为3.2 s,吸水管道内的流速为0.75 m/s,真空罐内的稳定工作压力为-11 533 Pa,吸入真空罐内的水量为9 600 mm2,排水时间为2.5 s,吸/排水周期时长为5.7 s,该真空吸鱼泵的吸捕速率计算值为6.06 m2/h。需注意的是,因实际工作过程中真空吸鱼泵的吸水口处设有止回阀或其他截止阀门,第一次吸水结束后吸鱼管道内的水仅少量回流,所以真空吸鱼泵设计计算中的吸水时间应为数值模拟得到的吸水时间与水充满吸鱼管道所用时间的差值。

4 结论

基于VOF模型,以抽气速度为边界条件,对真空吸鱼泵的吸水和排水阶段进行了数值模拟,得到了速度、压力、相分布等流场信息。通过数值模拟,可以得到准确的吸水时间、吸程、真空罐内压力、吸水管道内流速、抽气速度等的关系以及排水时间,进而根据此数值开展真空吸鱼泵设计,而且可以极大缩短开发时间,降低开发成本,因此数值模拟是设计真空吸鱼泵非常有效的手段。

由于本研究的物理模型根据实物进行了一定比例缩放,数值模拟结果尚不能指导实际真空吸鱼泵设计,下一步将按照真空吸鱼泵实际尺寸进行等比例三维建模,并进行数值模拟研究,更加有效地辅助真空吸鱼泵设计。