基于压缩感知的密封端面声发射信号提取技术研究*
2023-10-07张尔卿
张尔卿 陈 平 周 燕
(中密控股股份有限公司 四川成都 610045)
机械密封是一种旋转轴封装置,常用于压缩机、反应釜等装置[1-3]。其工作原理是通过密封端面摩擦副动、静环的贴合、旋转、补偿来实现阻漏的过程,因此密封端面的接触状态决定着机械密封的性能。机械密封在运转状态时,因端面摩擦会产生一定频段的声频,且不同摩擦副材料、不同运行转速或不同端面状态下,摩擦所产生的声音频率不同,因此可以通过摩擦副声发射信号数据判断摩擦副的运行状态,从而监测机械密封是否失效[4]。
声发射(Acoustic Emission,AE)检测是一种无损检测方法,其信号属于高频剧变信号,对数据采样频率要求较高,一般采集的声发射数据数量巨大且存在数据冗余,非常不利于数据的传输,需要通过数据降维再恢复的方法提高数据传输效率[5-6]。压缩感知(Compressive Sensing,CS)是一种寻找欠定线性系统稀疏解的技术,由CANDES等在2006年提出,常被应用于信号处理中,可进行信号压缩、剔除冗余信息和降维降噪等,也用于重构稀疏和信号恢复等[7]。
本文作者将压缩感知技术应用于机械密封端面声发射信号传输过程,利用压缩感知相关算法对原始AE信号进行压缩,再通过重构算法将压缩后的AE信号进行恢复,对比原始AE信号与重构信号的相似度,以探究机械密封端面声发射信号的压缩传输效果。
1 压缩感知原理
1.1 压缩感知
压缩感知的理论主要分为稀疏表示、信号压缩、信号重构3个部分,其中信号稀疏表示是压缩感知理论成立的前提条件,信号压缩是数据传输过程的关键步骤,信号重构是压缩感知的最终目的[8]。压缩感知算法流程图如图1所示。

图1 压缩感知算法流程Fig.1 Flow of compressed sensing algorithm
1.2 信号稀疏表示
信号的稀疏表示是指经过稀疏变换后的信号中非零元素尽可能减少,如果一个N×1的信号里,非零元素不超过k个,那么该信号可称为k-稀疏信号,因此信号通过稀疏变换后是离散信号[9]。
在实际采集信号过程中,往往信号都不是以稀疏的形式存在的,为了便于信号的处理,提高计算效率,则需要对原始信号进行稀疏变换。对于采集的原始信号X=[x1,x2,…,xN]T为N×1长度的列向量,稀疏变换基Ψ=[ψ1,ψ2,…,ψN]为N×N维矩阵,其中的任一元素ψn=[ψ1n,ψ2n,…,ψNn]T为N×1长度的列向量,则信号X可以表示为
X=ΨΘ
(1)
其中Θ=[θ1,θ2,…,θN]T,当Θ中有k个非零元素时,且k≪N时,则Θ为k-稀疏信号,同时Θ也称为原始信号X的稀疏表示[10]。
从公式(1)中可以看出,信号的稀疏表示的k值与Ψ密切相关,稀疏变换基Ψ也称为稀疏矩阵或稀疏字典,压缩感知理论在不同领域中研究最广泛的就是如何找到合适的字典。目前稀疏字典主要分为两类,固定字典和学习字典[11]。其中比较典型的固定字典有傅里叶字典、离散余弦字典等[12]。快速傅里叶变化(FFT)的核心就是将时域信号转换为频域信号,因此在频域较少的信号中,FFT对信号的稀疏效果是非常好的。离散余弦变换(DCT)是离散傅里叶变换(DFT)的一种特殊形式,DCT省略了DFT中的复数运算,通过构造偶函数的方式来实现,相对于DFT,DCT具有较好的频域聚集度,可以将不重要的频域信号去掉[13]。K-奇异值分解(K-SVD)是一种比较主流的学习算法,其综合了k-means算法和奇异值分解(SVD)算法的思想,利用SVD算法对误差项进行分解,将分解得到误差最小项作为修正系数对字典元素进行更新,经过迭代得到最优解[14-16]。
1.3 信号压缩
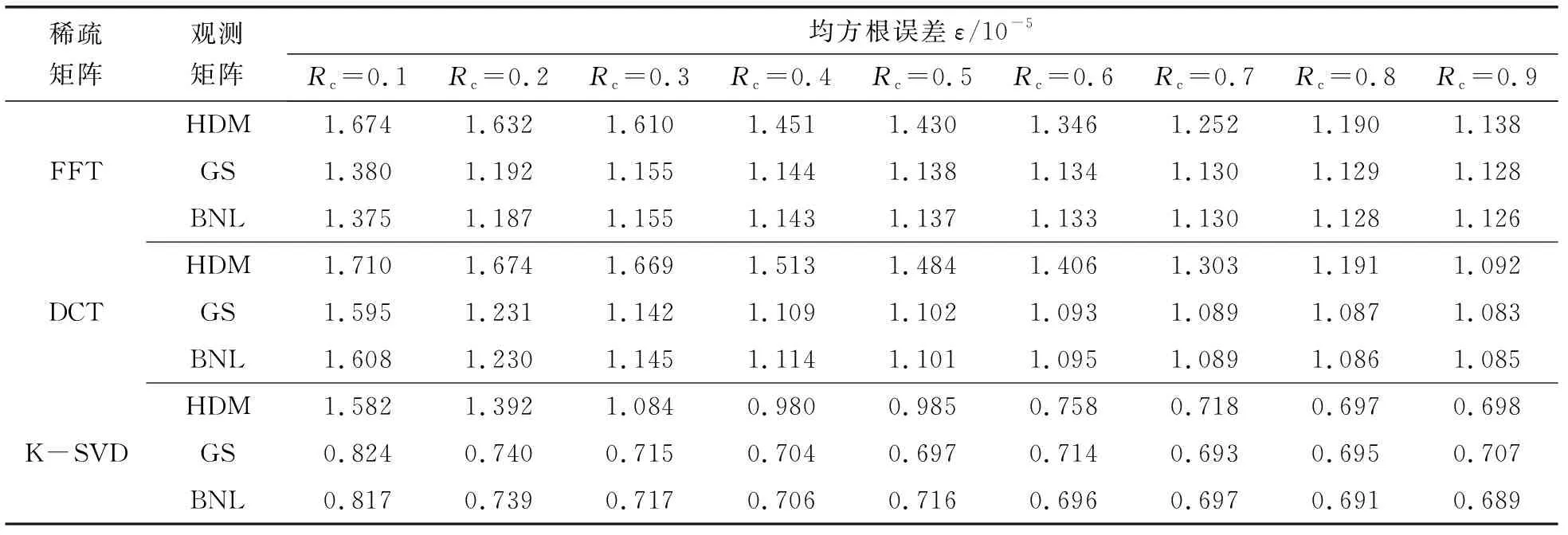
信号稀疏表示后虽然可以简化计算,但信号的维度并没有降低,稀疏系数Θ仍然是N维数据,对于数据传输效率并没有得到优化。这里引入一个与稀疏矩阵Ψ不相关的观测矩阵Φ,观测矩阵Φ=[φ1,φ2,…,φN]为M×N维矩阵,其中的任一元素φn=[φ1n,φ2n,…,φMn]T为M×1长度的列向量,且要求M Y=ΦX (2) 即: (3) 其中Y=[y1,y2,…,yM]T。由式(2)可以明显看出,通过观测矩阵Φ与原始信号X的乘积,得到了压缩后的信号Y,信号数量从N个降低到了M个,由于M 信号压缩完成后即可将数据进行传输发送至服务终端,最后就是将接收到的数据进行信号重构,信号重构相当于对公式(2)中,已知Y和Φ的值,求解线性方程组得到X的值,但由于M A=ΦΨ (4) 即: Y=ΦΨΘ=AΘ (5) 从式(2)和式(5)可以看出,这里方程将求X值转变为求Θ,然后通过间接的方式求得原始信号X,因为Θ是稀疏信号,极大地减少了未知量,优化了问题求解过程。因此将信号重构问题转化为 (6) 根据式(6)求得Θ值后,代入式(1)中,即可重构出信号X′,将原始信号X与重构信号X′进行对比,用均方根误差(RMSE)来判定X与X′相似度,再根据信号压缩比(CR)进行综合评判,找到适合机械密封声发射信号传输过程的最优压缩感知算法。 均方根误差如式(7)所示。 (7) 压缩比如式(8)所示。 Rc=M/N (8) 贪婪算法是一种主流的信号重构方法,其基本思想是利用迭代的方式重建信号的支撑集,通过某种贪婪准则,求得待估信号构成的元素,贪婪算法可以显著降低计算的复杂程度[19]。正交匹配追踪(OMP)是一种常用的贪婪算法,它主要有识别、增强、残差更新3个阶段,通过反复迭代计算信号的支撑集,不断更新残差系数,最终获得重构信号[20-21]。 实验设备采用国内某知名企业机械密封运转实验台,机械密封采用双端面机械密封,动、静环材料选用石墨-硬质合金组合,润滑介质采用油润滑,声发射探头安装在机械密封外压盖开孔处,要求尽可能贴近动、静环处,机械密封声发射信号采集实验台如图2所示。 图2 机械密封声发射信号采集实验台Fig.2 Mechanical seal acoustic emission signal acquisition test bench 声发射数据采集前需要预先拟定实验参数。实验设置最大静压为3.8 MPa,开机转速为1 480 r/min。设置采样频率为1 MHz,每10 s保存一次信号采集文件。机械密封声发射采集传输实验流程图如图3所示。 图3 机械密封声发射采集传输实验流程Fig.3 Flow of acoustic emission acquisition and transmission experiment of mechanical seal 文中的核心旨在研究机械密封声发射信号传输效率和数据恢复效果,因此实验数据分析最重要的环节在信号压缩和信号重构2个阶段。 信号压缩的关键是寻找合适的稀疏矩阵Ψ和观测矩阵Φ,稀疏矩阵Ψ会影响稀疏系数Θ的稀疏程度,从而间接影响信号重构的效果。稀疏矩阵Ψ和观测矩阵Φ需要保证RIP有点等距性质,RIP性质的等价条件是保持稀疏矩阵Ψ和观测矩阵Φ不相关性。 提取实验采集时长10 s的原信号数据,其声发射信号的长度为106,如图4所示。 图4 声发射原始信号波形Fig.4 Acoustic emission original signal waveform 在实现压缩感知算法过程中,信号的稀疏性对重构的效果至关重要,波形从时域到频域等空间域的转换,可以对实验装置的特有声频突出显示,同时可以排除不存在的声频和淡化周围环境噪声,信号从时域到频域的转化也是对信号稀疏的过程。从图4中明显可以看出,声发射信号是由不同频率的声波叠加而成,这里利用FFT和DCT对原始声发射信号进行稀疏表示,效果如图5所示,其中图5(a)为快速傅里叶变换后的效果,图5(b)为离散余弦变换后的效果。 图5 声发射信号稀疏表示效果Fig.5 Sparse representation effect of acoustic emission signal: (a)FFT;(b)DCT 对比图4和图5可以发现,稀疏表示后的信号大部分值都明显趋近于0,而声发射频域等空间域信息被明显突出。从图5(a)、(b)中可以看出,不同的稀疏算法,对信号的稀疏分布也不一致,也会直接影响信号重构的效果。通常在实际信号应用中,声发射的频域是非常复杂的,可能会出现大量声频的情况,使得信号在FFT或DCT变换后达不到稀疏的效果或稀疏效果很差,使得重构信号的误差很大。而学习字典可以在不同工况环境条件下,自适应地去寻找信号的稀疏表示,得到在有限训练样本条件下,输出最好的算法模型用于信号重构。在压缩感知算法中,不同的压缩比对信号的稀疏系数也会有很大的影响,文中主要研究压缩比为0.1~0.9之间声发射信号的重构效果,以K-SVD算法为例,分别选取压缩比Rc为0.1和0.9时的信号稀疏系数效果示意图如图6所示。 图6 K-SVD的声发射信号稀疏信号效果Fig.6 Acoustic emission signal sparse signal effect of K-SVD:(a)Rc=0.1,K=40;(b)Rc=0.9,K=40:(c)Rc=0.1,K=480;(d)Rc=0.9,K=480 对比图6(a)和图6(b),在压缩比不同时,稀疏信号的频率和幅值看不出明显的差别。而对比图6(a)和图6(c)可以发现,训练样本集K值越大时,其信号稀疏程度更大。除此之外,与FFT和DCT不同的是,K-SVD稀疏表示后的信号数量会减少,这与选择的训练样本集K值有关,当训练样本K=40时,稀疏表示后的信号数量为19 531个;而当训练样本K=480时,稀疏表示后的信号数量为234 375个。 压缩比的大小同时也决定着观测矩阵的大小,压缩信号的长度与观测矩阵的行数相等,因此观测矩阵的选择与信号重构效果也有直接关系。文中主要运用部分哈达玛矩阵、高斯随机矩阵和伯努利随机矩阵作为观测矩阵,渐变云图可以很清楚地显示各种矩阵特征情况,分别选取矩阵中100×100像素大小图像进行观察,其图像效果如图7所示。 图7 观测矩阵渐变云图效果Fig.7 Observation matrix gradient cloud image effect:(a)partial Hadamard matrix;(b)Gaussian random matrix;(c)Bernoulli random matrix 图7(a)为部分哈达玛矩阵,该矩阵是由±1组成的正交矩阵。图7(b)为高斯随机矩阵,该矩阵数值的随机概率符合正态分布的特点,从图像中也可以清楚地看出大部分的数值接近于0。图7(c)为伯努利随机矩阵,该矩阵也是由±1组成,但与部分哈达玛矩阵不同的是,+1和-1的概率均为50%且随机分布,从图7(a)和图7(c)的纹理分布也可明显看出。以上3种观测矩阵对信号进行压缩处理时的运算效率以伯努利随机矩阵最快,其次为部分哈达玛矩阵,最后是高斯随机矩阵,但它们处理数据的速度都在秒级。任意一种稀疏矩阵和这3种观测矩阵组合,以处理10 s一个通道的声发射数据为例需要的最长时间依次为:伯努利随机矩阵需要2.35 s,部分哈达玛矩阵需要3.64 s,高斯随机矩阵需要7.38 s。 信号重构的目标是将压缩后的信号恢复成原始信号,其原理是通过重构算法,将压缩信号Y转化求解得到稀疏系数Θ,再利用已知的稀疏矩阵Ψ与稀疏系数Θ相乘,便可求得重构信号X′。 采用不同稀疏矩阵Ψ、观测矩阵Φ以及不同压缩比时,信号重构的效果是不一致的,信号重构效果的好坏可以用均方根误差(RMSE)来进行判定。如图8所示。 图8 在不同压缩比下的重构均方根误差Fig.8 Reconstruction root mean square error under different compression ratios:(a)partial Hadamard matrix:(b)Gaussian random matrix;(c)Bernoulli random matrix 对比图8(a)、(b)、(c)可以看出,采用部分哈达玛矩阵作为观测矩阵重构的均方根误差值整体偏大,高斯随机矩阵和伯努利随机矩阵的重构效果非常接近。由于伯努利随机矩阵是由+1和-1组成的,相对于高斯随机矩阵而言,降低了计算难度,提高了计算效率,因此在效果相近的情况下优先选择伯努利随机矩阵。 通过K-SVD算法求得的稀疏矩阵计算均方根误差值整体较小,特别在压缩比为0.2~0.4左右时,均方根误差值为(1.021~1.047)×10-5,信号压缩量较大且信号重构效果较好,此处K-SVD选取的训练样本K值为40,该算法用于重构信号的效果也与选取K值的大小有关。因此针对K-SVD算法,选择伯努利随机矩阵,在不同压缩比、不同训练K值情况下,重构均方根误差效果曲面图如图9所示。 图9 K-SVD重构效果Fig.9 K-SVD reconstruction effect 由图9可以看出,随着训练样本和压缩比的增大,其均方根误差值明显减小,信号重构性能提升。但对于文中压缩感知的根本目的是为了解决声发射信号传输问题,若训练样本较多时,会增大数据运算量,降低程序运行效率。而压缩比较大时,会影响信号压缩效果,信号传输效率也无法提高。从图9中可以发现,三维曲面梯度下降最快点在压缩比0.2~0.4、训练样本集数量80~160的位置,因此在该范围内信号重构性能最佳。这里取Rc=0.3、K=120,稀疏矩阵采用K-SVD算法、观测矩阵采用伯努利随机矩阵,重构算法采用OMP算法,声发射信号原始采集信号与重构信号对比效果如图10所示。 图10 声发射信号重构效果对比Fig.10 Comparison of reconstruction effect of acoustic emission signal 从图10中可以看出,重构信号曲线(红色曲线)对原始信号曲线(蓝色曲线)的拟合效果是非常好的,基本还原了信号的波形、轮廓及峰谷形状,均方根误差为7.16×10-6。 针对机械密封声发射信号,采用不同稀疏矩阵和观测矩阵,基于OMP算法进行重构,对于不同压缩比,其压缩感知重构性能参数如表1所示。 表1 机械密封声发射信号压缩感知重构性能参数Table 1 Mechanical seal acoustic emission signal compression sensing reconstruction performance parameters 从表1中也可以明显看出,K-SVD-GS-OMP和K-SVD-BNL-OMP的重构效果最好,考虑到伯努利随机矩阵的运算效率是高于高斯随机矩阵的,因此对于声发射信号重构采用K-SVD-BNL-OMP算法是最优的,再考虑到其信号压缩和信号传输的综合性能,因此选择训练样本集K=80~160,压缩比Rc=0.2~0.4的重构效果最优,其均方根误差值为(7.06~7.39)×10-6,小于压缩比0.2时的平均基准值1.28×10-5,满足工业现场应用基本要求。 提出一种基于压缩感知的密封环声发射数据降维方法,即利用稀疏矩阵将采集的原始AE数据进行稀疏表示,再通过观测矩阵将稀疏表示后的AE数据进行压缩采样以达到降维的目的,数据传输完成后利用OMP等信号重构算法将压缩后的信号恢复。在某些特定工况条件下,对采集原始声发射信号进行不同算法处理,对比不同算法对信号数据压缩和重构效果,探究适用于机械密封声发射信号的最优算法,以应用于信号传输。主要结论如下: (1)对于稀疏矩阵的研究表明,在频率较少的信号波形中,使用FFT正交基和DCT正交基的信号稀疏表示效果较好。但对于复杂的机械密封声发射数据而言,使用K-SVD的重构效果明显优于FFT正交基和DCT正交基。 (2)对于观测矩阵的研究表明,使用部分哈达玛矩阵的整体重构误差值较大,高斯随机矩阵和伯努利随机矩阵的重构效果非常接近,但在算法计算量和运行效率上,伯努利随机矩阵是优于高斯随机矩阵的。 (3)综合考虑信号压缩率和重构效果,当选择训练样本集K=80~160,压缩比Rc=0.2~0.4时,选择K-SVD作为稀疏矩阵,伯努利随机矩阵作为观测矩阵,采用OMP算法的信号重构效果最佳,其均方根误差为(7.06~7.39)×10-6。1.4 信号重构
2 实验数据采集
2.1 实验设备

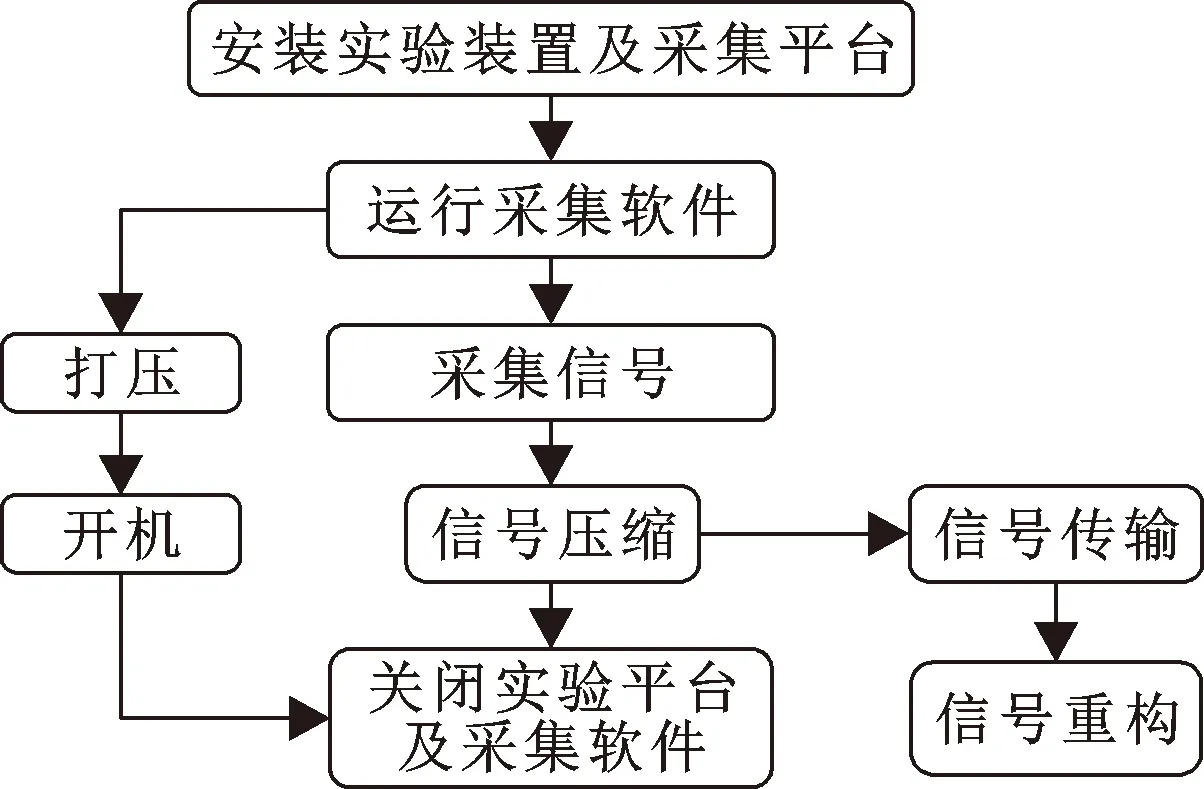
2.2 实验参数及过程
3 实验数据分析
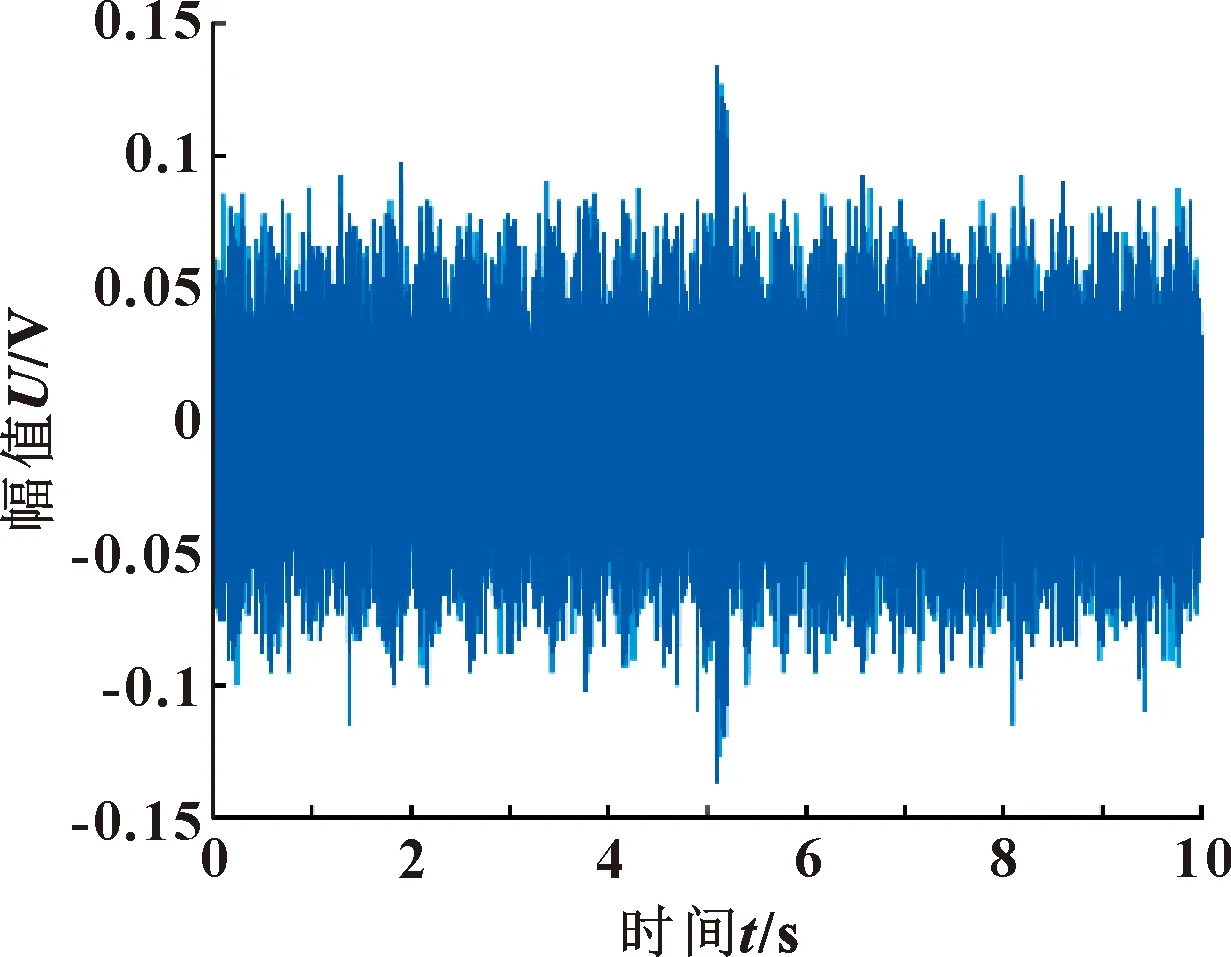
3.1 信号压缩阶段



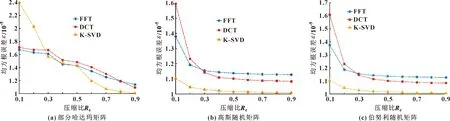
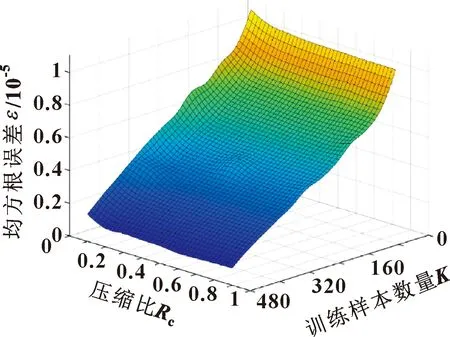
3.2 信号重构阶段

4 结论
