活塞环/缸套摩擦副表面织构优化设计方法*

张 迪 顾春兴

(1.上海海事大学商船学院 上海 201306；2.上海建桥学院机电学院 上海 201306；3.上海理工大学机械工程学院 上海 200093)

近年来，作为提高摩擦表面界面性能的有效途经之一，表面织构已经成为表面工程领域和摩擦学领域的研究热点，但是表面织构的机制研究以及织构优化设计方法尚未完善。随着织构结构参数及分布参数的不断优化，织构化摩擦副的性能明显提升，逐渐在活塞环-缸套系统、轴承、机械密封、切削刀具及表面织构仿生设计等工业领域得到应用[1]。

理论和试验研究表明，应用表面织构可以有效改善摩擦学系统的摩擦学性能，但不同织构的结构参数及分布参数会对摩擦副性能产生不同的影响，只有设计合适的表面织构才能保证织构化摩擦副具有优异的性能[1]。例如，ZHANG等[2]研究发现，与规则圆形特征织构相比，子弹形或鱼形织构特征具有更低的摩擦因数。目前的织构特征优化工作多局限于给定分布工况下织构化摩擦副性能的对比，而以优化算法为基础的织构特征优化工作还不完善。

本文作者提出了一种面向活塞环/缸套摩擦副的表面织构优化设计的新方法。基于该方法，在活塞环表面设计深度随机变化的微织构(每个微织构具有其各自的深度)，以满足与活塞环/缸套系统性能相关的不同性能目标，如降低油膜剪切力；通过分析这些织构方案的性能变化，确定了取得最优性能的织构设计方案。

1 数学模型

活塞环/缸套系统可能处在混合润滑模式或者流体动压润滑模式下。混合润滑模式是一种既有流体动压润滑又有微凸体接触的润滑模式[3]，因此其理论模型中也要包括这两部分。

1.1 流体力学

为了计算流体压力，文中采用了具有JFO(Jacobsson-Floberg-Olsson)空化边界条件的二维雷诺方程[4-5]。其方程[6]如下所示：

(1)

流体饱和度θ和油膜压力p之间的关系可由公式(2)揭示：

(2)

根据文献[6]可知，采用FBNS方法求解流体润滑模型，其计算速度将明显快于传统方法(2个数量级)。

1.2 接触力学

预测微凸体接触压力的微凸体接触模型有很多，其中应用最广的是GT(Greenwood Tripp)模型。GT模型的表达式[10]为

(3)

式中：E′是接触表面的等效弹性模量；F2.5(λ)是与膜厚比λ有关的统计学公式；ηβσ和σ/β是两组与微凸体及表面粗糙度有关的参数，其中，η为微凸体密度，m-2，β为微凸体半径，m。

根据前人的研究成果[11-12]，针对一般工程摩擦副表面通常可以假设ηβσ=0.04和σ/β=0.001。

F2.5(λ)可通过拟合公式计算给出：

F2.5(λ)≈

(4)

1.3 润滑油流变模型

润滑油的黏度受很多因素的影响，它对油膜压力和摩擦功耗有重要的影响。影响润滑油黏度的最重要因素是润滑油压力和润滑油温度。相应的公式[13-14]如下：

(5)

μ1=μ0exp{(lnμ0+9.67)[(1+5.1×10-9p)α-1]}

(6)

式中：T是润滑油温度；a0、T1、T2都是相应的修正参数。

文中润滑油的牌号为5W40。因此，a0=0.043 65 mPa·s，T1=1 393 ℃，T2=149.2 ℃。其中，参数α是与润滑油属性相关的，该参数通常可以取0.68。

1.4 摩擦力和摩擦功耗计算

在织构系统中，总摩擦力ftot可由如下公式表示：

ftot=fvis+fasp

(7)

其中，流体摩擦力的计算公式为

fvis=

(8)

式中：φf、φfs和φfp都是摩擦力相关的流量因子，相应的计算公式见文献[8]。

由微凸体接触引起的摩擦力的计算公式为

(9)

式中：κasp是微凸体摩擦因数；文中取κasp=0.12。

2 结果和讨论

2.1 模拟条件

油膜厚度h(x，y)的表征是混合润滑模型数值计算的关键。其表达式如下：

h(x，y)=h0+hpro(x，y)

(10)

式中：hpro(x，y)是轮廓；h0为最小油膜厚度。

文中模拟以活塞环/缸套系统作为研究对象。因此，无织构活塞环/缸套系统的轮廓可用如下表达式表示：

(11)

式中：b为活塞环的轴向宽度；δ为活塞环的桶高，文中活塞环桶面高度设为6 μm。

对于织构化活塞环/缸套系统的轮廓(织构特征为凹坑)，其表达式为

(12)

式中：hp代表织构特征的深度；rp为织构特征的半径。

织构特征均匀分布在活塞环表面，如图1所示，x和y位于全局坐标系中，而x′和y′位于织构特征中心的局部坐标系中。文中的目的是为了通过优化各个织构的深度来减少摩擦副的摩擦力，为了节约计算时间，考虑到活塞环/缸套模型的对称特性，仅对1/2模型进行计算。模型示意图如图1所示。

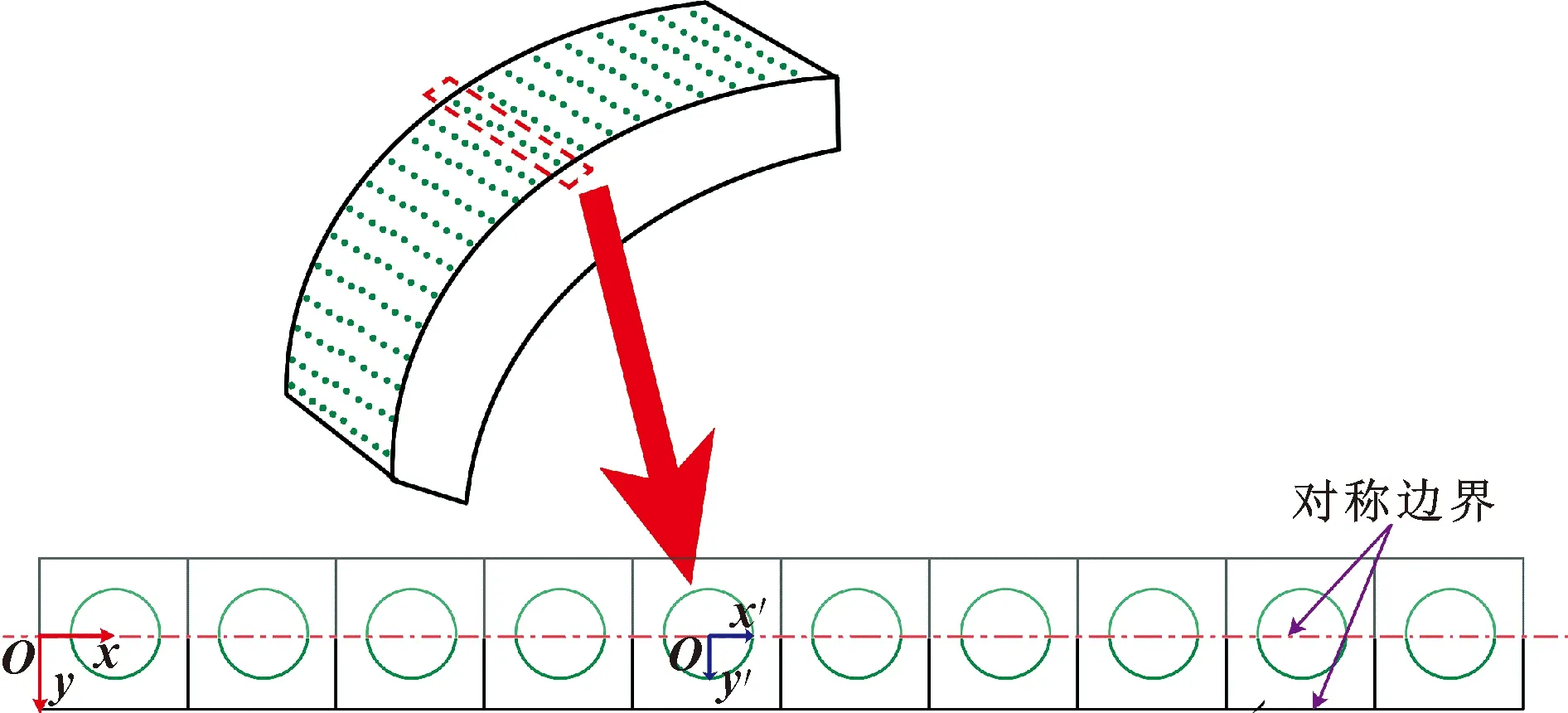
图1 建模示意Fig.1 Schematic of modeling

此外，织构特征的尺寸和分布显著影响织构系统的摩擦磨损性能。当织构特征尺寸小于赫兹接触尺寸时，引入表面织构能给摩擦学系统带来减摩效果[15-18]。反之，表面织构会增大摩擦学系统的摩擦力[19-21]。因此，文中织构的宽度设为60 μm。外载荷固定，所诱导的平均压力为0.1 MPa。表1给出了数值模拟条件。

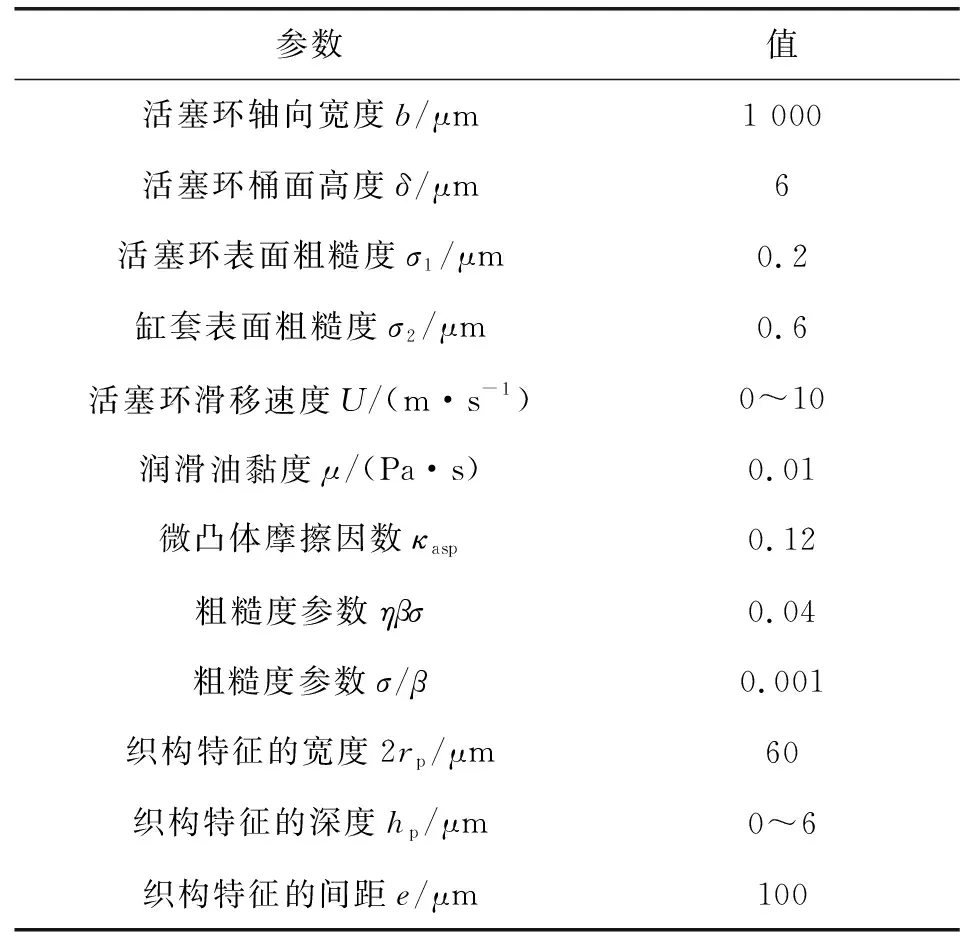
表1 数值模拟条件Table 1 Numerical simulation conditions

2.2 模型验证

为了验证计算模型的正确性，将文中模型的计算结果与文献[22]中的理论结果进行了对比，文中所采用的模拟条件与文献[22]中的条件一致。如图2所示，采用当前模型所预测的结果与文献中的结果一致。

图2 文中模型及文献流体压力分布计算结果比较Fig.2 Comparison results of hydrodynamic pressure distribution between the model in this paper and literature

2.3 性能评价指标及优化算法

为了评估在活塞环表面设计织构对摩擦副性能的改进，文中以摩擦力为评价指标。即织构化活塞环/缸套系统的性能优化目标是减少其摩擦力，从而确保其满足更高效的运行条件。

通过应用优化算法可以获得能改善活塞环/缸套系统性能的织构设计方案。文中将织构的深度作为随机变量，即每个微织构都有自己的深度，可以自由更改。因此，优化过程旨在随机改变每一个微织构的织构深度，直到达到目标函数的最小值。目标函数可由如下的性能指标确定：

(13)

其中上标ref表示用于比较的参考值，即对应于无织构活塞环/缸套系统的结果。

目标函数具有不同的局部极小值，因此织构参数的优化设计需要使用全局搜索算法。同时，织构参数的优化设计需要对混合润滑模型进行多次求解，网格细化和采用质量守恒空化边界条件会引起润滑模型不易收敛和计算时间过长的问题。因此，有必要寻找一种能够保证搜索系统全局最优值以及润滑模型快速求解的方法。

针对鸟群觅食模型进行改进所提出的粒子群算法(Particle Swarm Optimization，PSO)因为需设置的参数少且计算结构简单，目前已经在实际工程中得到广泛的应用[23]。应用粒子群算法时，仅需要设置惯性权重系数ω、自我学习因子c1和社会学习因子c2的值。ω直接影响着算法搜索能力的强弱，ω越大，全局搜索能力越强，局部搜索能力越弱；ω越小，局部搜索能力越强，全局搜索能力越弱。文中选取双曲正切曲线来控制ω的变化，在搜索初期其递减速度较慢，给粒子充分的时间进行大范围的全局搜索，减小陷入局部最优的情况；中期近似线性递减，逐渐加强局部搜索的能力；后期变化率再次减小，着重细致的局部搜索，精准确定全局最优解[23]。此外，当c1>c2时，粒子的运动更偏向个体最优的方向，反之则更偏向群体最优方向。优化算法初始阶段着重突出粒子的自我认知能力，注重粒子运动的遍历性，减小陷入局部最优解的概率；随着迭代的进行，加强粒子间的交流，使种群最优解的位置对每个粒子的运行起到更大的影响，着重对最优解的附近进行局部搜索。参数变化策略[23]如下：

(14)

(15)

(16)

式中：kmax是最大迭代次数；k是当前迭代次数；ωmax、ωmin分别是惯性权重系数的最大值和最小值，文中取ωmax=0.95，ωmin=0.4；c1max、c1min分别是自我学习因子的最大值和最小值，c2max、c2min分别是社会学习因子的最大值和最小值，文中取c1max=2.5和c2max=2.5，c1min=1.25和c2min=1.25。

随着迭代次数k的增加，ω不断减小，c1逐渐减小，c2逐渐增大。这样设置就满足了初期注重粒子在空间上的遍历性，增强全局搜索能力，在迭代次数过半时，加强粒子间的交流，增强局部搜索的能力。

为了解决由网格细化和采用质量守恒空化边界条件引起的润滑模型不易收敛和计算时间过长的问题，文中通过结合Fischer-burmister-Newton-Schur (FBNS)方法和网格细化策略，来求解润滑方程，详见文献[24]。

文中将无织构案例中获得的摩擦力数值作为参考值，然后改变微织构深度，计算不同参数下的摩擦力，直到找到改善活塞环/缸套系统性能的最佳织构设计方案。微织构深度可以在最小值和最大值之间变化，即hp，min=0(无织构)和hp，max=6 μm。即优化的边界条件为

hp，min≤hp≤hp，max

(17)

2.4 摩擦力分析

文中以摩擦力作为评价活塞环/缸套摩擦副性能的指标。通过大量的数值分析计算，不同速度工况下活塞环织构化设计的最优方案如图3所示。织构方案A是10 m/s速度工况下的最优设计方案，织构方案B、C、D、E分别是5、2、1、0.1 m/s速度工况下的最优设计方案。为了更清楚地揭示织构分布特征，图3中也显示了各织构沿着Y=0处的膜厚分布。可以发现，在相同外载荷作用下，不同滑移速度工况下活塞环/缸套摩擦副的最优织构设计方案均不相同。

图3 不同滑移速度下各织构方案织构分布(左图)和Y=0处膜厚分布(右图)：(a)织构方案A，滑移速度10 m/s；(b)织构方案B，滑移速度5 m/s；(c)织构方案C，滑移速度2m/s；(d)织构方案D，滑移速度1 m/s；(e)织构方案E，滑移速度0.1 m/sFig.3 Texture distribution(left)and film thickness distribution at Y=0(right)of different texture schemes under different speeds：(a)texture scheme A at speed of 10 m/s；(b)texture scheme B at speed of 5 m/s；(c)texture scheme C at speed of 2 m/s；(d)texture scheme D at speed of 1 m/s；(e)texture scheme E at speed of 0.1 m/s

图4对比显示了不同速度工况下无织构活塞环/缸套摩擦副和织构化活塞环/缸套摩擦副的压力分布。速度在10～0.1 m/s之间变化，织构方案分别采用图3中的不同速度工况下的最优织构设计方案。从图4中可以发现，织构的存在显著影响压力分布；与无织构活塞环/缸套摩擦副的预测结果对比，具有最优织构设计方案的活塞环/缸套油膜压力具有更宽的压力分布范围。

图4 不同滑移速度下非织构和织构活塞环/缸套系统油膜压力分布：(a)非织构，滑移速度10 m/s；(b)织构方案A，滑移速度10 m/s；(c)非织构，滑移速度5 m/s；(d)织构方案B，滑移速度5 m/s；(e)非织构，滑移速度2 m/s；(f)织构方案C，滑移速度2 m/s；(g)非织构，滑移速度1 m/s；(h)织构方案D，滑移速度1 m/s；(i)非织构，滑移速度0.1 m/s；(j)织构方案E，滑移速度0.1 m/sFig.4 The hydrodynamic pressure distributions for non-textured and textured ring-liner system：(a)no texture at speed of 10 m/s；(b)texture scheme A at speed of 10 m/s；(c)no texture at speed of 5 m/s；(d)texture scheme B at speed of 5 m/s：(e)no texture at speed of 2 m/s；(f)texture scheme C at speed of 2 m/s；(g)no texture at speed of 1 m/s；(h)texture scheme D at speed of 1 m/s；(i)no texture at speed of 0.1 m/s：(j)texture scheme E at speed of 0.1 m/s

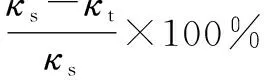
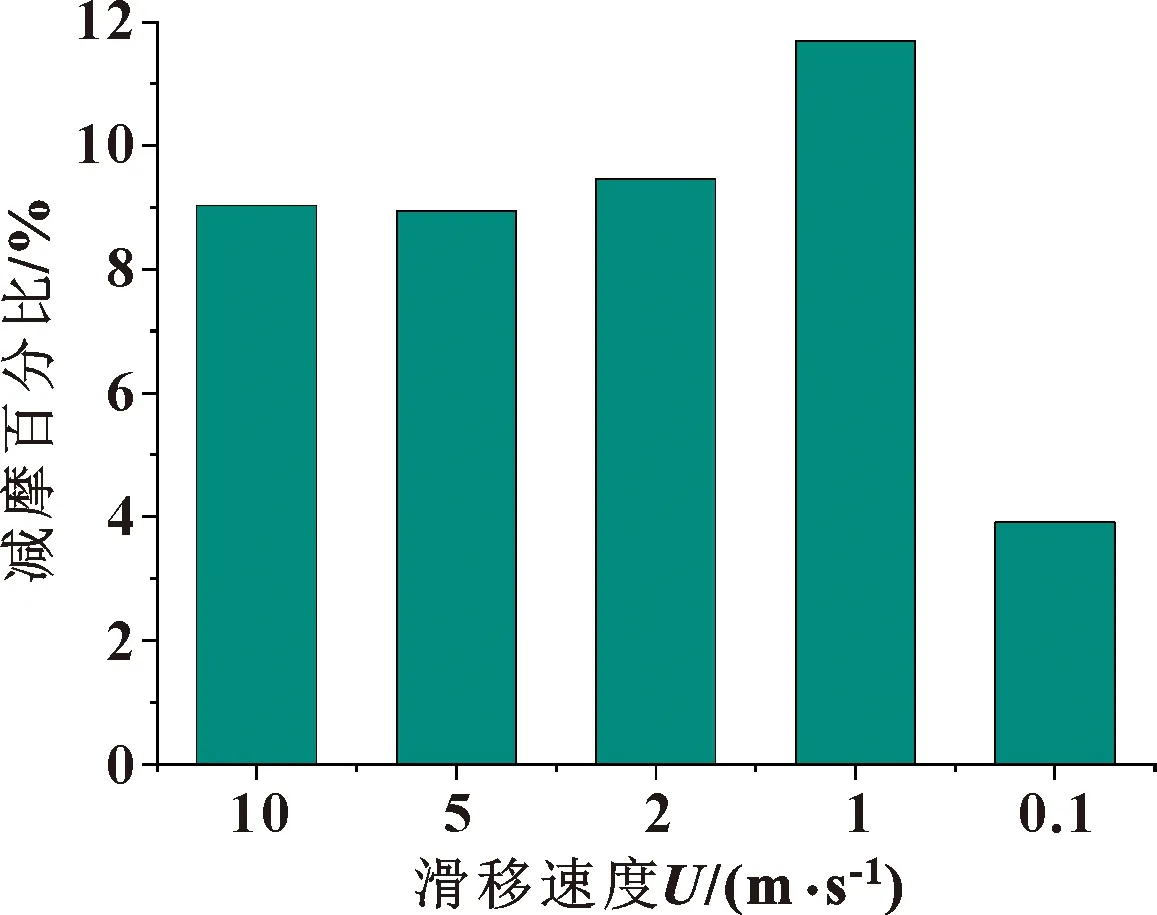
图5 不同滑移速度下最优织构方案的减摩百分比Fig.5 Friction reduction percentage of optimal texture schemes under different speeds

图6示出了不同速度工况下，具有最优织构方案和无织构方案的活塞环/缸套系统最小油膜厚度。可以发现，当速度从10 m/s到1 m/s时，具有最优织构方案的活塞环/缸套系统的最小油膜厚度比无织构的活塞环/缸套系统的最小油膜厚度有所增加。在相同载荷情况下，最小油膜厚度的增加，有利于减轻摩擦副的磨损。值得注意的是，当滑移速度为0.1 m/s时，最优织构方案的最小油膜厚度比非织构方案有所降低。当滑移速度0.1 m/s时，最小油膜厚度在1 μm左右，此时膜厚比λ≈1.6，摩擦副处于混合润滑状态。最小油膜厚度的减小将会加剧摩擦副磨损。因此，具有最优摩擦学性能的织构方案并不能保证摩擦副具有更好的磨损性能，表面织构的优化应考虑表面织构对摩擦和磨损的综合影响。

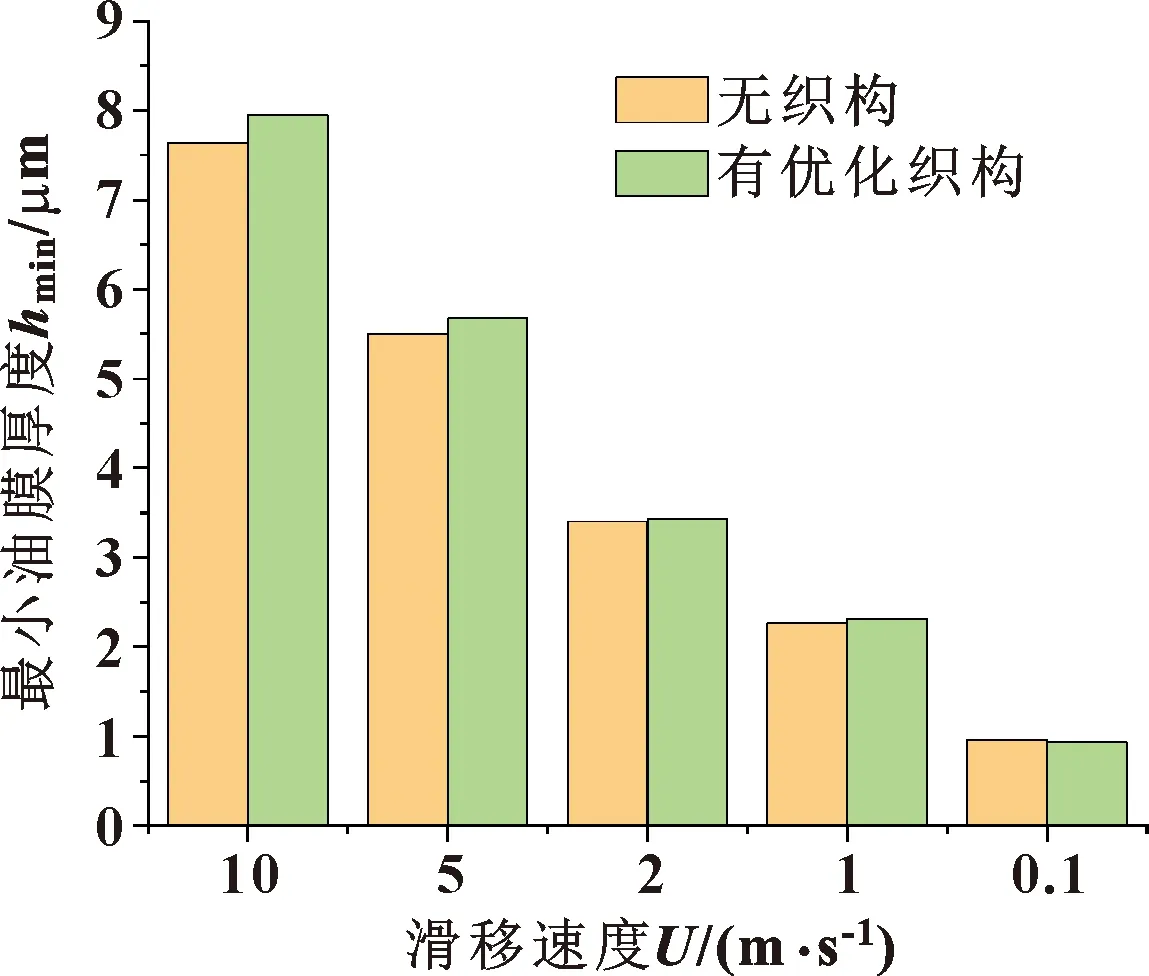
图6 不同滑移速度下最优织构方案与无织构方案的最小油膜厚度对比Fig.6 Comparison of minimum oil film thickness of optimal texture schemes and no texture scheme under different speeds

前文研究表明，不同滑移速度下最优织构方案均不相同。然而，对于同一个活塞环/缸套系统而言，在对活塞环表面进行织构加工后，其织构参数是不变的，而系统实际运行工况是时变的，如活塞环的滑移速度是变化的。对于某一速度工况下优化的表面织构设计方案并不能确保其在其他速度工况下也具有优异的性能。图7给出了某个单一速度工况下优化的织构设计方案在其他速度工况下的减摩效果。可以发现，在研究的工况下，织构方案E在多种速度工况下都具有良好的减摩性能，其减摩百分比为1%～10%。

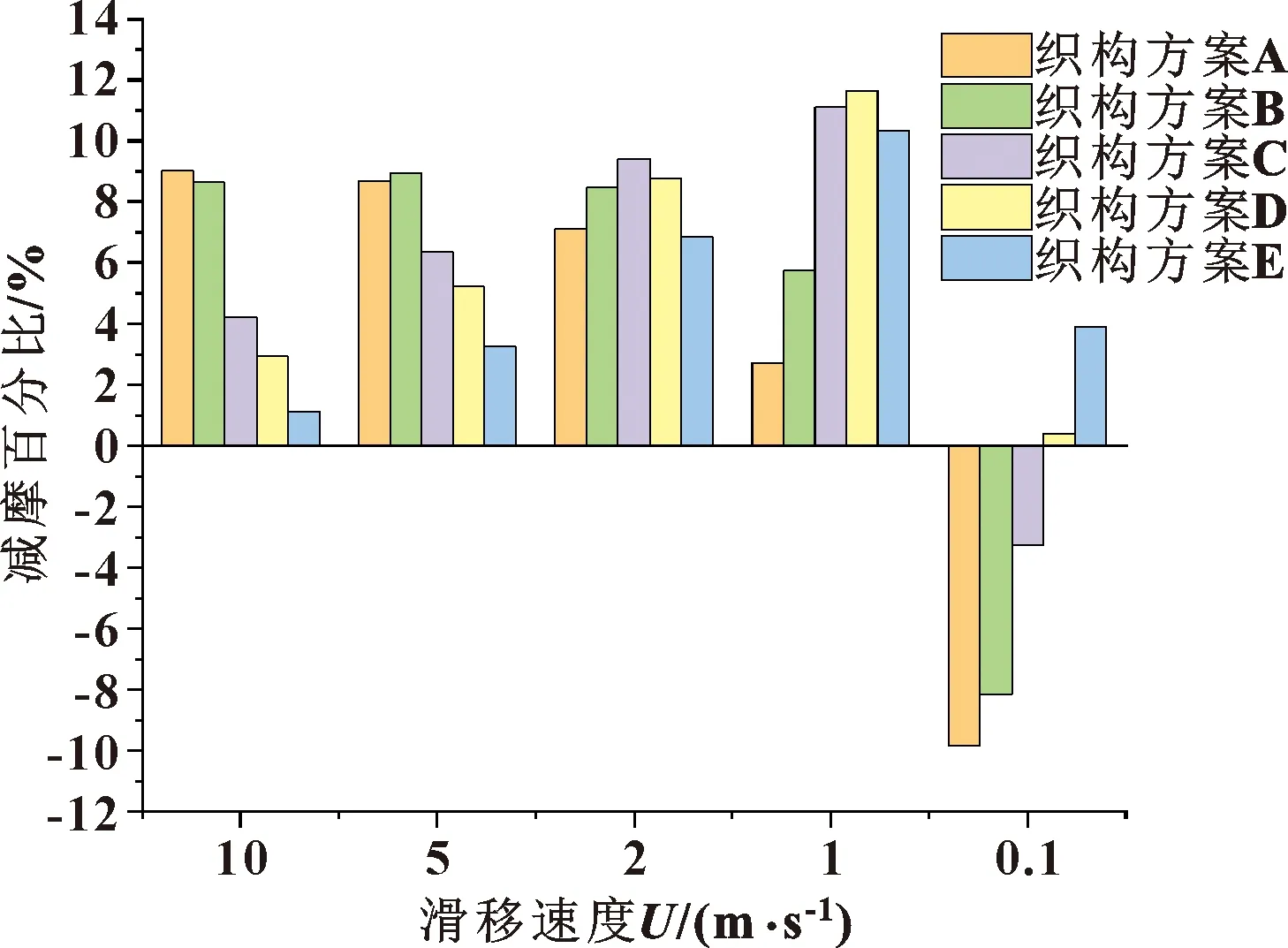
图7 不同织构方案在不同滑移速度下的减摩百分比Fig.7 Friction reduction percentage of different texture schemes under different speeds

表面织构的有效性受各种因素的交互影响，同一摩擦副在不同的操作条件也会具有不同的摩擦学特性，任何一个织构参数或操作条件的改变都可能导致原采用最优参数的织构系统具有相反的效果。因此当织构对象具有多种操作工况时，需要综合分析织构方案在各个工况下的效果，以确定最优织构方案。此外，面向经过数值模拟确定的织构参数还需要通过实验做进一步的评价。

3 结论

(1)提出一种面向活塞环表面设计不同深度微凹坑的新方法。以质量守恒润滑模型与微凸体接触模型为基础，建立了面向织构系统的混合润滑模型。在混合润滑模型的基础上，通过选择合适的活塞环/缸套摩擦副性能评估指标，确定优化活塞环/缸套摩擦副性能的目标函数，结合粒子群优化算法，完成了活塞环表面各个织构深度的优化设计。

(2)基于大量的数值模拟试验可以发现，适当的微凹坑分布可以提高活塞环/缸套摩擦副性能，从而提高活塞环/缸套摩擦副承载能力，降低摩擦力。基于这些结果，证明了所提出的织构优化设计方法可提高织构化活塞环/缸套摩擦副性能。