基于CFD方法的高线速度齿轮最优喷嘴布置角度设计*

2023-10-07夏建芳陈思雨王志伟胡小舟

润滑与密封 2023年9期

夏建芳姚恒陈思雨王志伟陶轩胡小舟

(中南大学机电工程学院湖南长沙 410083)

在高速齿轮传动系统中，通常使用喷油润滑的方式对传动系统进行润滑与冷却。然而随着齿轮转速升高，齿轮旋转所产生的气流会形成空气屏障，阻碍润滑油进入齿轮啮合点且使润滑油流束破碎[1]，导致啮合区的润滑油量减少，进而导致润滑效率降低。AKIN等[2-5]针对不同齿轮的不同啮合状态、喷油方向的喷油润滑进行了一系列的研究，发现润滑效率不仅与喷油参数和传动比参数有关，还受喷油位置和角度的影响。

如何对喷油润滑系统的相关参数进行设计以最大限度地提升润滑效率，减少系统使用的油量，同时保持齿轮箱的可靠性，了解齿轮箱内部的润滑油流场的动态特性是非常有必要的。目前普遍采用计算机仿真模拟的方法研究复杂箱体内流体的流动情况[6]。

2009年，ARISAWA等[7]首次采用油/空气两相流CFD(Computational Fluid Dynamics)方法对齿轮风阻与搅油损失进行研究，并证明该方法是研究高速齿轮风阻损失的有效工具。FONDELLI等[8]在2015年运用CFD方法模拟了齿轮喷油润滑过程，并评估了喷油润滑所产生的阻力扭矩。曹寓等人[9]在2017年在 FLUENT中采用 VOF模型及动网格技术进行流场动态仿真，得出了不同时刻齿轮箱内各个位置油液的体积分数以及油压、流速的变化规律，分析了不同喷油流量对齿轮润滑效果的影响。NIU、WANG等[10-14]先后利用CFX与Fluent软件建立了流体动力分析模型，研究了超高速齿轮喷油润滑时，各工况参数对油流束方向偏离乃至对润滑效率的影响，并给出了克服齿轮旋转引起空气屏障对润滑阻碍作用的方法。DAI 、CHEN等[15-17]先后通过商用CFD软件研究了喷嘴入射角度、喷嘴与啮合点距离等布置参数对润滑效率的影响，比较得出最优喷嘴布置方案。

目前，对于高速齿轮箱的润滑问题，主要是运用商用流体软件对齿轮箱内部的流体动态特性分析，以进一步优化喷油润滑系统的设计，但总的来说，开展的时间较晚，相关报道较少。虽然上述文献对喷嘴布置方式进行了相关研究，但多数是依靠经验设计试验方案，通过仿真分析比较各方案得出最优方案，这样不仅会花费大量的时间在仿真计算上，而且得到的只是设计方案的最优方案，并不是理论上的最优方案。

本文作者针对高线速度齿轮的喷油润滑问题，通过流体软件仿真研究了齿轮箱中流场的动态特性，对喷油润滑中齿轮旋转产生的气流与喷油流束的干涉问题进行分析，利用流场流线图寻找最优喷嘴布置角度，并研究喷嘴角度布置与齿轮传动比和转速的影响。

1 喷油润滑理论分析

1.1 湍流模型

齿轮喷油润滑过程中，流体为有旋流动，且流体在齿轮弯曲壁面上流动，流体有较大的应变率，故选择RNGk-ε湍流模型[18-19]。湍流动能k和湍流动能耗散率ε方程为

(1)

(2)

其中，

(3)

式中：ρ为流体密度；x和t分别为位移和时间分量；i、j为张量指标；μt是湍流黏性系数；μ是混合流体湍流黏性系数；R为净相变率；Gk是由平均速度梯度产生的湍流动能；Gb是由浮力影响产生的湍流动能；YM为可压缩湍流脉动膨胀对总的耗散率的影响；αk、αε分别为湍流动能和耗散率的有效普朗特数的倒数；Cμ、C1ε、C2ε、C3ε为模型常数，由Fluent软件给出。

1.2 VOF模型

VOF(Volume of Fluid)多相流模型是一种求解多相流动和自由表面流动的计算模型，引入各项流体体积分数来跟踪2个或多个不混溶流体区域的自由表面[20]。对于文中的润滑油-空气两相流系统，该方法分别求解流体运动的动量方程和计算域内相分布的体积分数方程，由于仅由润滑油或空气占据的控制体积域分别具有0或1的体积分数，故2种不混溶的流体(润滑油-空气)之间的界面位置可以根据计算域内的体积分数分布来确定，每个控制体积域内的流体物理参数是在平均流体体积分数的基础上计算的[21]：

(4)

式中：φ代表流体的物理参数；α代表体积分数，且α1+α2=1。

2 齿轮箱内部喷油润滑流场计算模型

2.1 几何模型

文中采用直齿轮啮入侧喷油进行研究，表1给出了其几何模型和基本工况参数。为避免啮合区网格之间尺寸相差过大导致网格畸变进而导致计算出错，将齿轮对的中心距扩大1 mm。

表1 齿轮箱几何参数和工况参数Table 1 Gometric parameters and working condition parameters of gearbox

2.2 流场计算模型

将齿轮对导入Ansys Spaceclaim中，抽取流体外壳作为齿轮箱内部流体域。为了提高仿真准确性以及清晰地表征喷油流束的流动情况，需要将喷油流束流经的路径进行网格加密。故将润滑油流束流过的路径取一圆柱(如图1(a)所示)，再与原流体域进行布尔运算相减，形成中间与外部2个部分的流体域，并采用共享拓扑的方式，使2个流体域共用边界面。目的是使2个流体域网格共节点，在仿真过程中的网格重构中更加流畅，并减少结构中的边界面数量。在Ansys Meshing模块中，将外部流体域采用默认的网格划分方式，识别曲率与临近度，将内部流体域的网格加密到0.5 mm，最终网格数为2 766 997(如图1(b)所示)，并导入到Fluent模块。

图1 流体计算域几何结构与网格处理示意Fig.1 Schematic fluid domain geometry and mesh processing： (a)geometry；(b)mesh

Fluent软件仿真的主要设置如下：时间选项为瞬态，采用VOF多相流模型，打开隐式选项，湍流模型选择RNGk-ε模型，临近壁面选择标准壁面函数，材料中引入润滑油与空气分别作为多相流中的两项，喷嘴出口为速度入口，水力直径为2 mm。底部作为压力出口，所有墙面都是用非滑动静止壁面条件。求解器中，压力速度耦合采用标准SIMPLE算法，梯度差分选项中选择最小二乘方法，压力选项中选择PRESTO！，湍流动能选项中选择二阶迎风格式。

Some relations between prime inner operators,prime closure operators and connections

齿轮转动采用动网格技术进行模拟，采用铺层法与局部重构法对网格进行控制，选择齿轮对为动网格控制区域，选择区域类型为刚体。运算时间步长为1×10-6s。

3 最优喷嘴角度的提取方法与验证

3.1 最优喷嘴角度的提取

图2所示是润滑油体积分数渲染图，为了显示啮合区的润滑油分布，将小齿轮透明化显示。图片中表明润滑油能够顺利进入啮合区进行润滑与冷却，图3(a)所示是齿轮箱内速度矢量分布，速度矢量能够表示齿轮箱内各点上的速度方向与大小，流场整体的速度矢量分布能够区域性地表示齿轮箱内的空气流动状况。图3(b)所示是齿轮箱底部视角的速度矢量分布，可以看出齿轮在啮合处有部分的轴向流动，且在齿轮边缘速度矢量会集中在齿轮的齿宽中心。

图2 润滑油体积分数渲染Fig.2 Rendering of oil volume fraction

图4所示为齿轮中间截面上的速度流线，速度流线是与流场中每一点上的速度矢量相切的曲线，代表了流场中各点的流动路径，区别于速度矢量图，流线图更强调质点运动的连续性。图4(a)所示是正常工况下截面上的流场流线，齿轮高速旋转在齿顶周围形成了空气屏障，喷油流束突破了空气屏障进入到齿轮啮合区进行润滑；在喷油过程中，空气屏障与喷油流束发生干涉，导致流入啮合区的油量减少，流体动力损失增大，润滑效率降低；同时，喷油流束也影响了齿轮周围的空气流动状况。

因此，为了研究齿轮原始工作情况下周围的空气流动状况，调出停止喷油齿轮空转时的速度流线图(如图4(b)所示)，发现除了在啮合区上方之外，其他区域的空气流动都与图4(a)相似。将图4(b)中方框部分的啮合区上方流线放大(如图5所示)，可以看出，齿轮对旋转分别产生的空气屏障在啮合区上方发生干涉并结合成一条进入啮合区的路径，该路径将引导气流进入啮合区。如果将润滑油沿该方向射入，会最大程度地减少空气屏障干涉所引起的润滑油流失和喷油流束破裂，并减少流体动力损失，点B为气流首次冲击齿面的接触点。

图5 齿轮空转时啮合区上方的流线放大图Fig.5 Enlarged view of flow field streamline in meshing area without oil injection

提取出图5中的理想角度，如图6(a)所示。R(Ra)、r(ra)分别为大齿轮与小齿轮的分度圆半径(齿顶圆半径)，点A为喷嘴出口，点B为气流与齿面的接触点，也是气流进入啮合区的入射点。AB连线与垂直方向上的夹角即理想喷嘴角度为7.37°，流线中提取出的理想角度路径并不通过分度圆相切点C，这是因为气流首先冲击齿面，随后由齿面旋转带动到啮合点，同时流线失去连续性。

图6 喷嘴角度设置示意Fig.6 Schematic of nozzle angle：(a)geometric distribution of the measured optimal angle；(b)traditional nozzle deflection setting

图6(b)所示是目前传统的喷嘴角度设置[14-15]，喷射流方向指向点C，偏角α为喷嘴出口与点C连线与垂直方向的夹角。当喷嘴按照该设置方式布置时，喷油流束将在点D冲击未啮合齿面，导致油流束破碎乃至进入啮合区的油量减少以及喷油流束的冲击动量降低，从而润滑效率降低。

3.2 最优喷嘴角度的润滑效率验证

如图7所示，为了验证提取出的理想角度是否拥有最高的润滑效率，分别设置图6(b)中α角为5°、0°、-5°，以及图6(a)中理想角度，进行了仿真模拟。

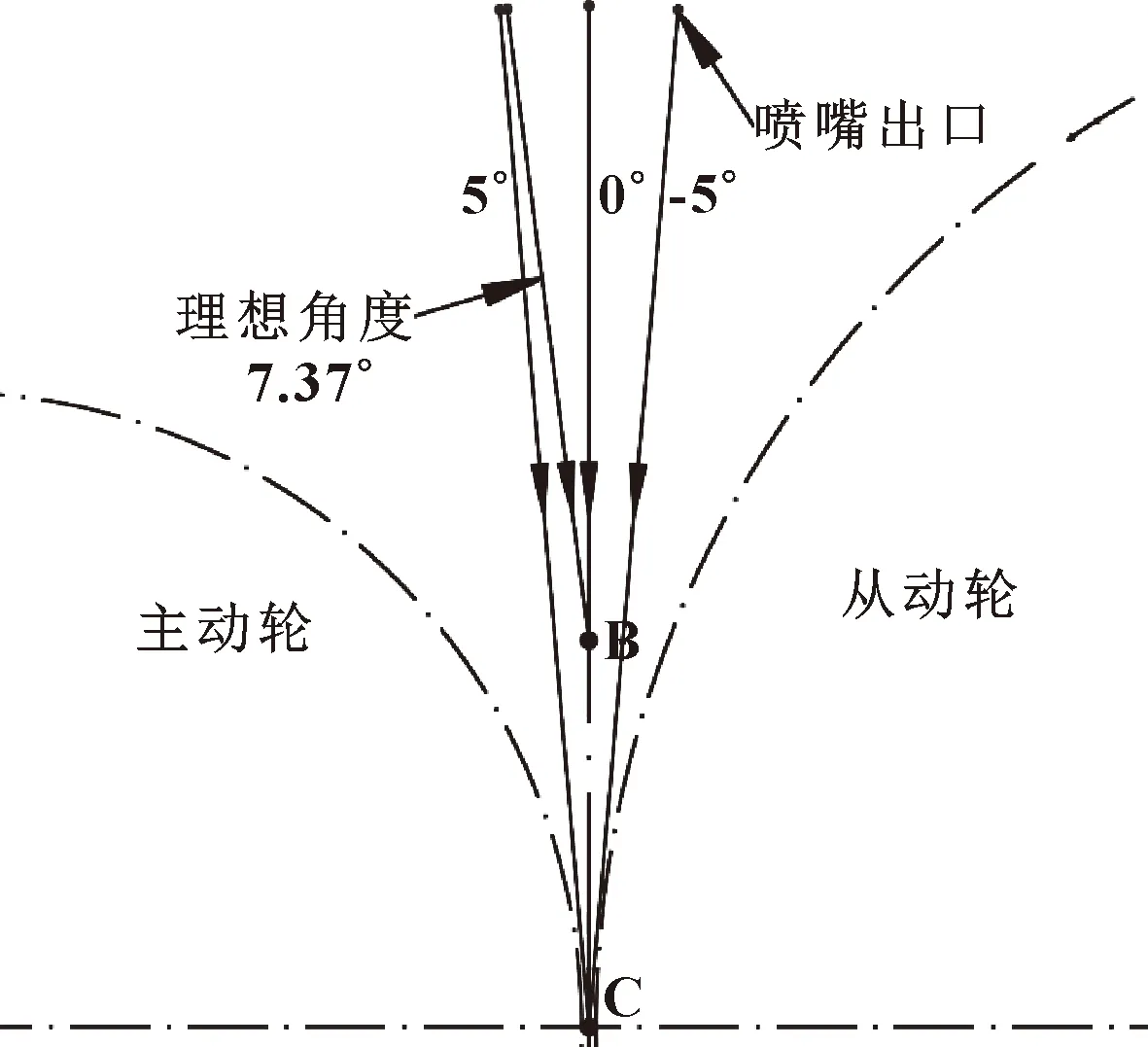
图7 4组喷嘴角度设置Fig.7 Four sets of nozzle angle settings

图8所示是分别在4组喷嘴角度设置下小齿轮上的润滑油体积分数云图。可以看出，按照理想角度设置的组别齿轮啮合区润滑油体积分数更大，润滑油油量更大，分布更集中于啮合中心区。喷嘴角度为5°时的润滑油分布较分散，这是因为偏转的角度过大，润滑油首先喷到小齿轮还未啮合的齿面上，导致啮合区的体积分数较少。直齿轮传动的重合度一般不大于2，工作中啮合状态的齿面数不超过2，所以润滑油需要集中在啮合状态的1到2个齿面上。喷嘴角度为0°和-5°时润滑油分布比5°时稍好，但仍较分散，且啮合齿面上的润滑油体积分数不高。按照理想喷嘴角度布置时，润滑油集中在啮合区的少数齿，证明润滑油的冲击深度很深，润滑效果在几组中最好。

图8 4组喷嘴角度设置的润滑油在小齿轮上的体积分数分布云图Fig.8 Contour of volume fraction distribution of lubricating oil on pinion of four sets of nozzle angle settings： (a)5°；(b)0°；(c)-5°；(d)optimal angle 7.37°

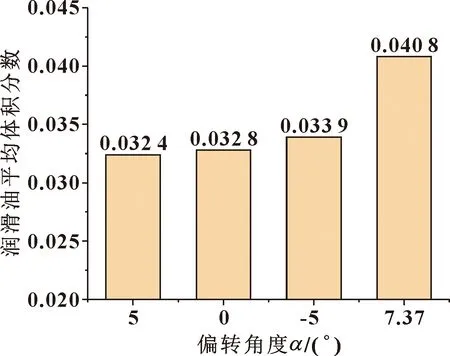
图9 4组喷嘴角度设置的润滑油平均体积分数Fig.9 Average volume fraction of lubricating oil of four sets of nozzle angle settings

文献[17]中表明，啮合区附近油压可视为判断齿轮润滑性能的标准。图10所示是小齿轮上的油压分布。可以看出，喷嘴按照理想角度7.37°设置时，啮合区拥有最大负压(绝对值)，即吸入润滑油的能力最强，另外3组在啮合区的负压大小与分布状况相似，但在小齿轮进入啮合区前的齿面上出现了正压峰值区域，这是润滑油流束喷至齿轮时产生的接触压力。α=5°时，啮合区前齿面压力峰值区域最大，且峰值最高；α=-5°时，峰值区域最小，峰值最小。这是因为α=5°时喷嘴向小齿轮偏转的角度过大，润滑油流束先冲击了小齿轮上的未啮合齿，并没有顺利进入啮合区。而α=-5°时，喷嘴向大齿轮偏转，先冲击大齿轮上的未啮合齿，故小齿轮上没有压力峰值区域。

图10 4组喷嘴角度设置时小齿轮上油压分布Fig.10 Oil pressure distribution on pinion of four sets of nozzle angle settings：(a)5°；(b)0°；(c)-5°；(d)optimal angle 7.37°

同时输出啮合区球体内的平均正压、平均负压、平均压力，如图11所示。在齿轮旋转时，旋转产生的气流在啮合处产生负压，形成卷吸效应，将润滑油吸入啮合区进行润滑，所以啮合区负压是促进润滑油吸入啮合区的主要因素。从图11可以看出，喷嘴按照理想角度7.37°设置时，啮合区平均负压、平均压力(负值)的绝对值最大，平均正压最小，吸入润滑油的能力最强因而润滑效率最高，验证了当喷嘴按照由流线提取出的理想喷嘴角度布置时拥有最高的润滑效率。

图11 4组喷嘴角度设置时的油压统计数据Fig.11 Oil pressure statistics of four sets of nozzle angle settings

4 不同工况参数对喷嘴角度设置的影响

为了研究齿轮几何特征和各工况参数对喷嘴角度设置的影响进而分析齿轮箱内的空气流动规律，设置不同的齿轮传动比与转速进行了仿真分析对比。

4.1 传动比对喷嘴角度设置的影响

传动比影响着齿轮的几何尺寸，文中保持小齿轮齿数不变，大齿轮齿数变化(按表2中设置)进行仿真，不设置喷油、不加载荷，使齿轮空转，小齿轮转速保持为9 800 r/min，其他设置不变，提取出齿轮中间截面的啮合区速度流线图，如图12所示。

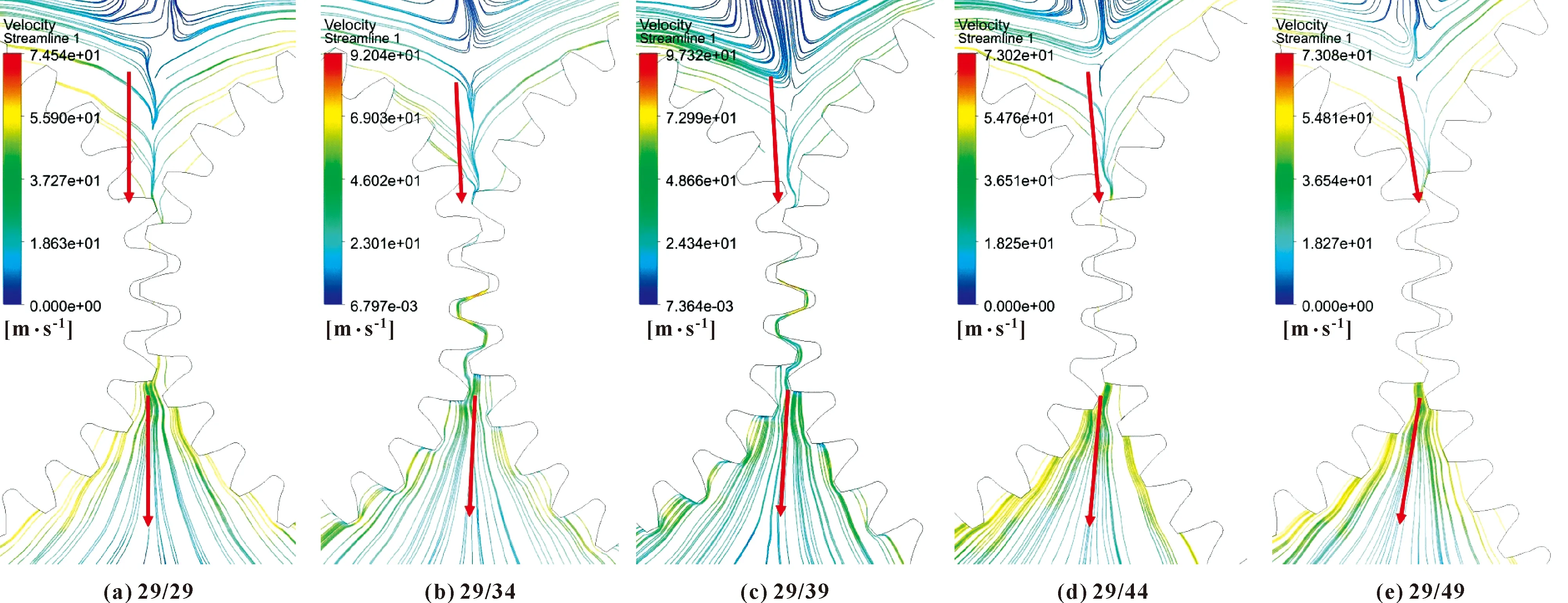
图12 不同齿数比下啮合区流线Fig.12 Streamline of meshing area under different tooth ratio：(a)29/29；(b)29/34；(c)29/39；(d)29/44；(e)29/49

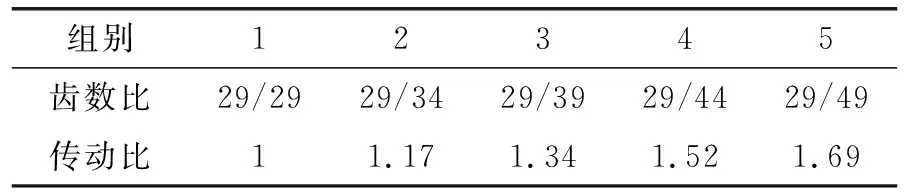
表2 不同组别转动比的设置Table 2 Gear ratio settings of different groups

如图12中的箭头所示，当传动比为1(29/29)时，啮合区上方的流线垂直向下进入啮合区，啮合区下方的流线同样也是垂直向下流出。当传动比增大时，上方流进啮合区的流线路径以及下方流出啮合区的流线路径均逐渐向小齿轮偏转，且流入流出路径沿齿轮中心距连线对称。将图中路径角度提取出来并拟合(见图13)，发现当传动比从1(29/29)逐渐增大到1.69(49/29)，进入啮合区的流线路径逐渐向小齿轮偏转，与垂直方向夹角从0°增大到7.37°，且偏转角度与传动比呈正相关，拟合后的一次函数方程为

图13 传动比与拟合区上方流线偏转角度的关系Fig.13 Relationship between gear ratio and streamline deflection angle above fitting area：(a)streamline angle above the meshing area of 5 groups of different gear ratios：(b)relationship and fitting curve between deflection angle and gear ratio

y=9.761x-9.177

(5)

已经验证进入啮合区的流线路径即为最优喷嘴布置角度，所以以上结论同时说明，当传动比增大时，最优喷嘴布置角度也同样向小齿轮偏转，且与传动比呈正相关。在传动比为1时，最优喷嘴角度为垂直向下喷油。

4.2 转速对喷嘴角度设置的影响

齿轮几何特征改变时，流场中的流动状况发生变化。为了研究在几何特征不变时流场中流动情况是否会因为其他工况参数的变化而变化，还需要对不同转速的传动组合进行研究。文中在齿数比为29/49保持不变，小齿轮转速分别设置为1 450、2 900、4 350、5 800 r/min进行仿真，分别调出啮合区的流场流线，如图14所示。

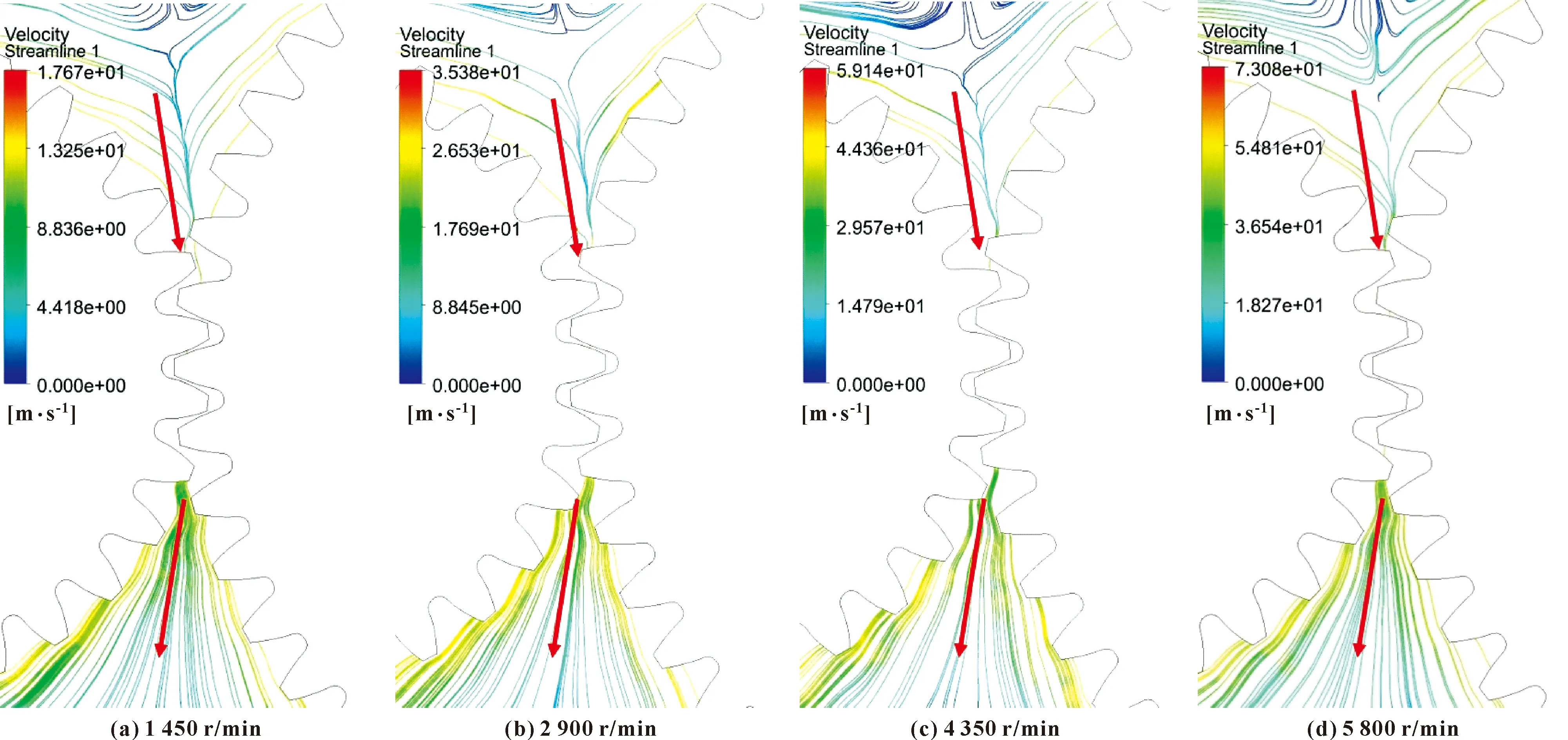
图14 不同转速下啮合区流线Fig.14 Streamline of meshing area at different speeds：(a)1 450 r/min；(b)2 900 r/min；(c)4 350 r/min；(d)5 800 r/min

如图14所示，齿轮转速变化时，齿轮箱内的流线分布变化不大，即空气流动的分布变化不大。从红色箭头看，进入啮合区的路径偏转角度几乎不变，且流出路径与流入路径沿中心距连线对称。

图15所示是啮合区上方流线偏转角度与转速的关系。随着转速增大，啮合区上方的迹线偏转角度变化不大，最大偏转角度在转速为2 900 r/min时为7.89°，最小偏转角度在转速为5 800 r/min时为7.37°，差距小于7%。这说明在齿轮喷油润滑系统中，当转速设置变化时，不需要重新调整喷嘴角度。

图15 啮合区上方流线偏转角度与转速的关系Fig.15 Relationship between streamline deflection angle and rotational speed above meshing area

从目前的仿真结果来看，转速的大小只与啮合区附近空气的流动速度有关，与分布状况与流动方向无关，故不影响最优喷嘴角度的设置，这也说明最优喷嘴角度只与齿轮几何结构有关，与工况参数设置无关。WANG等[11]研究认为，齿轮转速增大会影响喷油流束的正常流动，导致偏转。这是因为齿轮周围旋转形成的气流的速度增大会破坏润滑油流束维持原有圆柱状流束的能力，与此同时，齿轮空转时周围的气流分布与流动方向并没有发生改变。