油封正态分布结构参数的可靠性灵敏度分析*

夏靖炜 张付英 马 骏 张志祥 刘元刚

(1.天津科技大学机械工程学院 天津 300222；2.天津市轻工与食品工程机械装备集成设计与在线监控重点实验室 天津 300222；3.天津市科技发展服务中心 天津 300000)

油封又称为旋转轴唇形密封，被广泛应用于机械设备旋转轴的密封，其作用是阻止润滑油泄漏和防止外界杂质进入密封腔体。油封失效不仅会引起润滑油泄漏污染环境、降低机械零件的工作性能和设备工作效率，还会增加拆卸和维修成本，因此油封的密封可靠性对提升机械设备的运行效率至关重要。油封的密封性能一般由摩擦扭矩和泵吸率2个指标表征，摩擦扭矩过大，会导致工作时密封界面的温度升高，容易造成油封材料的老化和润滑油性能的恶化，从而降低油封的密封能力；泵吸效应产生的泵吸率则是反映油封动态密封能力的主要指标，泵吸率大于0，润滑油从空气侧泵吸回油侧，油封处于密封状态，泵吸率小于0，则油封会发生泄漏，因此，通常将泵吸率作为油封密封的可靠性指标。

近20年来，有关油封的泵送机制和泵送率研究取得了显著成果。SHEN和SALANT[1]研究了不同密封表面粗糙度类型组合时的非对称切向变形对泵送率的影响。JIA、董慧芳等[2-3]通过构建唇形密封的数值计算模型，分析了不同转轴表面加工方法对泵送的影响规律，并进行了转轴表面结构的参数化研究。吴庄俊[4]研究了径向唇形密封的密封性能，推导出唇形密封的泵吸率计算公式。江华生[5]分析了唇口表面周向弹性变形、操作参数和表面微条纹结构参数对泵吸率的影响。但在相关文献中，从泵送率角度判断油封可靠性的研究相对较少。

油封的结构参数对其密封可靠性有着重要影响，为了深入分析各结构参数对可靠度的影响程度，常用可靠性灵敏度分析方法。可靠性灵敏度分析方法是可靠性分析的重要内容，它能更直观地展现出各个因素对可靠度的影响。HAFTKA等[6]最先提出计算结构系统的可靠性灵敏度分析方法；BJERAGER和KRENK[7]定义了敏感度的概念并使用一阶矩法计算了敏感度。为了提高计算灵敏度的速度，学者们相继提出了改进的一次二阶矩法、三阶矩法[8-9]。DE LATAILLADE等[10]提出使用蒙特卡洛法进行敏感度计算。乔红威、吕震宙[11]采用基于加权非线性响应曲面法的蒙特卡洛法分析了灵敏度。张义民等[12]将四阶矩和Edgeworth级数相结合，把单自由度非线性随机参数振动系统状态方程展开为标准正态分布公式，计算了正态分布参数可靠性灵敏度。

本文作者以油封的泵吸率为可靠性指标，运用正交试验和曲面响应法拟合油封泵吸率的极限方程，进而构建可靠性模型，采用二阶矩法和蒙特卡洛法分别计算基于均值和标准差的油封5种结构参数的可靠性灵敏度，对比2种算法的敏感度结果，分析各个因素对灵敏度影响。

1 油封可靠性灵敏度计算方法

可靠性灵敏度为失效概率的变化与输入变量分布参数变化的比率，是通过可靠度对基本随机变量的分布参数的偏导数计算得到的，有近似解析法和数字模拟法2种方法。一次二阶矩法因计算简单，计算精度可满足大多数工程需求，成为近似解析法中应用较广的方法；蒙特卡洛模拟法因对解析式的线性要求不高，连续性问题不必离散化，是适用范围很广的方法，但模拟次数N会影响计算结果。文中通过2种算法，确定和对比正态分布参数对油封可靠度和灵敏度的影响。

1.1 蒙特卡洛可靠性灵敏度方法

蒙特卡洛法(Monte Carlo法，简称MC法)计算可靠性PR时，是以概率统计为基础，采用数字模拟的方式进行结构可靠性分析[13]。

油封的可靠度概率pr、失效概率pf之间满足关系式(1)，如果油封的极限状态方程用式(2)表示，连续随机变量Z的联合密度函数记为fx(x)，则可靠性概率与失效概率分别如式(3)和式(4)所示。

pr+pf=1

(1)

Z=g(X1，X2，…，Xn)=0

(2)

(3)

(4)

若各变量X=(X1，X2，…，Xn)相互独立，联合累积密度函数Fx(x)=Fx(x1，…，xn)，则可靠概率的表达式可变换为式(5)。

(5)

通过联合密度函数fX(X)对基本随机变量X=(X1，X2，…，Xn)生成N个随机样本点，再将样本点代入功能函数g(X)求解。功能函数大于等于0，表示样本点落入有效域，如果落入有效域的样本点个数为Nr，运用频率Nr/N近似代替可靠度概率PR，那么结构的可靠度和失效概率可以分别表示为式(6)和式(7)。

(6)

Pf=1-PR

(7)

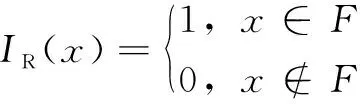
若用μi和σi分别表示第i个随机变量的均值和标准差，则蒙特卡洛法基于均值和标准差的敏感度计算公式分别如式(8)和式(9)所示。

(8)

(9)

可应用Matlab计算蒙特卡洛法的可靠性灵敏度，其计算流程如图1所示。

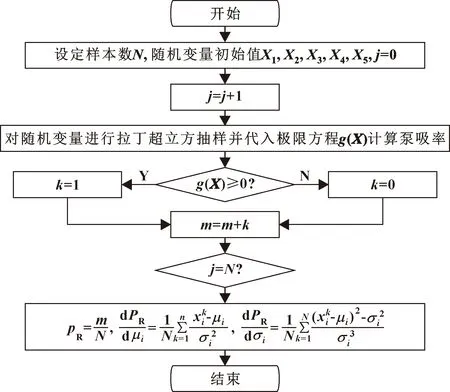
图1 蒙特卡洛法计算流程Fig.1 Calculation flow of Monte Carlo method

1.2 二阶矩法敏感度分析方法

二阶矩法是通过将随机变量均值点处的极限函数g(X)泰勒展开[14]，如式(10)所示，从而计算可靠性。

(10)

式中：Gi表示极限函数的i阶偏导在均值X=[X1，X2，…，Xn]的值。

均值μg和标准差σg的表达式分别如式(11)和式(12)所示。

(11)

(12)

式中：Var(X)为随机参数方差矩阵。

其可靠性指标和可靠度分别用式(13)和式(14)表示。

(13)

(14)

二阶矩法基于均值和标准差的灵敏度计算公式分别如式(15)和式(16)所示。

(15)

(16)

2 油封泵吸率的回归函数拟合

为了构建油封的可靠性模型，文中以泵吸率为输出值，油封的各个结构参数作为因子，基于正交试验和曲面响应法，进行油封泵吸率的回归函数拟合。油封在不同结构参数取值时的泵吸率计算，是通过有限元建模和数值计算集成获得的，具体模型建立，数值模型的验证和结果分析参阅文献[15]，文中不再赘述。

2.1 油封的结构及基本参数

研究的油封结构如图2所示，其基本参数如表2所示。

表2 油封的基本参数Table 2 Basic parameters of oil seal

图2 旋转唇密封结构Fig.2 Rotary lip seal structure

2.2 油封结构参数的正交试验

以油封的5种结构参数作为试验因子，泵吸率作为输出响应值，根据正交试验原理进行抽样，设计3水平5因子的正交试验表，并用A、B、C、D、E分别表示理论接触宽度R、油侧唇角α、空气侧唇角β、过盈量δ和腰厚t。过盈量在文中指单侧过盈量。表3所示为试验因子及水平。

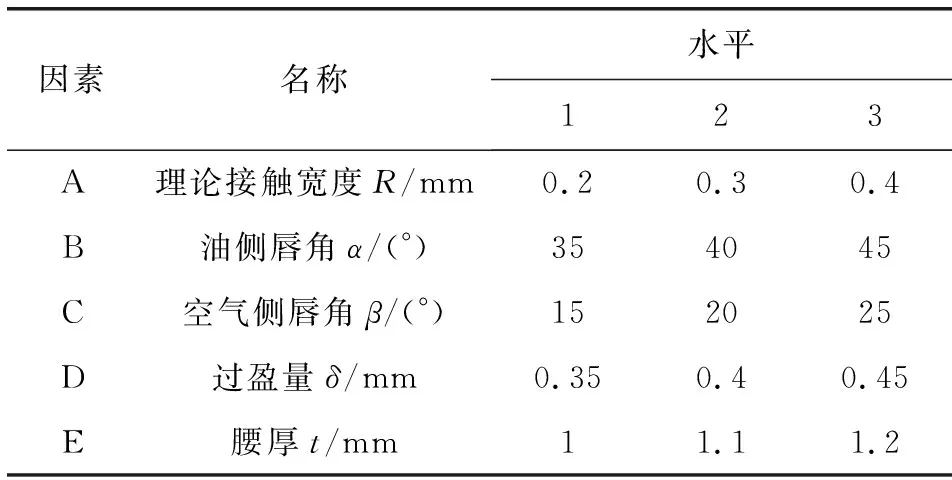
表3 田口试验因子和水平Table 3 Factors and levels of Taguchi test

将有限元建模和数值计算结果代入Mintab软件设计正交试验[16]，表4给出了正交试验设计及结果。

表4 正交试验设计及信噪比Table 4 Orthogonal experiment and SNR

2.3 基于曲面响应法的油封泵吸率函数建立

曲面响应法也称为回归设计，是优化随机过程的统计学试验方法，以综合实验技术为基础，通过数值模拟的方法寻找输出响应值与各个因素之间的近似表达式，即用结构响应面来替代失效面[17]。

目前的曲面响应函数大多采用二次回归方程进行拟合，其函数形式简单，引入的待定系数不多，在满足减少迭代计算的工作量前提下又能保证输入输出函数关系的准确性，函数形式如下：

(17)

式中：a0、bi、cij为待定系数，可通过最小二乘估计或内插法进行确定。

运用Mintab曲面分析对表4中的正交试验结果进行分析，非线性模型有线性+平方模型，线性+相互作用模型和完全平方模型，分析得出的回归剩余差分别为s=0.104 053，s=0.167 968，s=0.061 030 1，因此试验选择采用完全平方模型拟合回归函数。在初步拟合方程后，需要对模型进行简化。在模型的简化中要遵循排序原则，即显著项(P=<0.05)必须保留在模型中。因此，将模型中表现不显著的项及交互项剔除，再按照P值大小顺序依次剔除平方项，最后重新拟合模型。表5所示为简化后模型的方差分析结果。

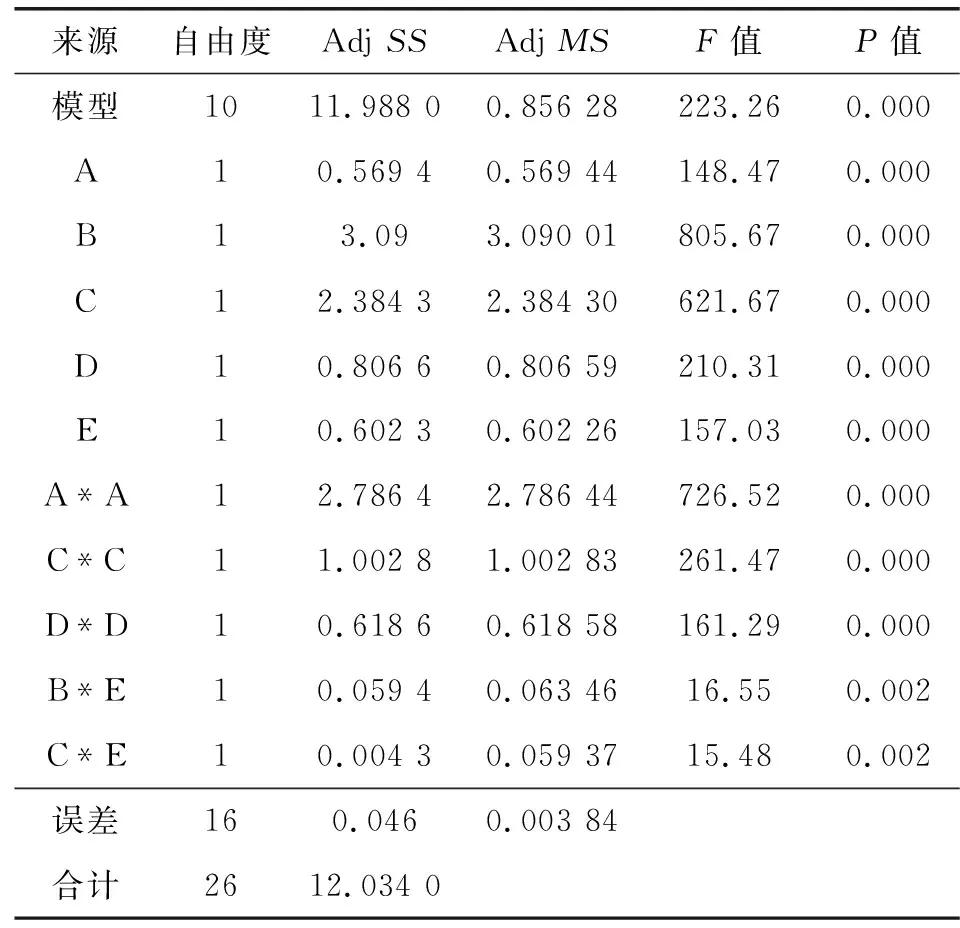
表5 泵吸率方差分析结果Table 5 Variance analysis results of pumping rate

泵吸率的回归模型如式(18)所示，式中X1、X2、X3、X4、X5分别表示理论接触宽度R、油侧唇角α、空气侧唇角β、过盈量δ和腰厚t。

Z=28.423 9-39.109 8X1+0.242 851X2-

0.140 677X3X5

(18)

3 油封的可靠性灵敏度分析

根据可靠性原理建立油封泵吸率的可靠性模型如下：

(19)

式中：R表示油封的可靠度；fx(X)为联合概率函数；g(X)表示油封的泵吸率极限状态方程，它表示油封的工作状态，当g(X)≥0时代表密封，反之，g(X)<0表示密封失效。

文中所研究的影响油封可靠性的结构参数均在油封制造过程中形成，因此假设这5种随机变量均服从正态分布，且参数之间互相独立，其分布如表6所示。

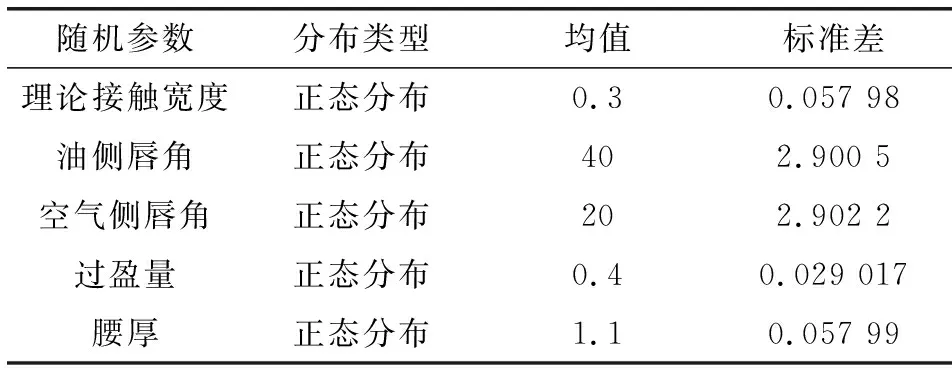
表6 结构参数分布Table 6 Structural parameter distribution

3.1 基于蒙特卡法的油封可靠性灵敏度计算

运用Matlab软件进行编程对油封的可靠性模型进行蒙特卡洛模拟。文中取N=10 000，计算得出使极限状态方程大于等于0的样本个数NR=99 987，因此可靠度概率为PR=NR/N，可靠性概率为PR=0.999 87，概率直方图如图3所示，可以看出分布呈现正态分布中的长尾分布，说明极限状态方程为正态分布。

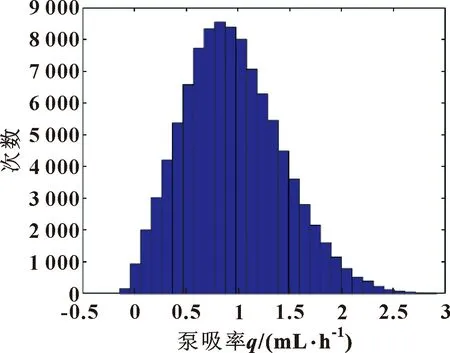
图3 泵吸率概率直方图Fig.3 Probability histogram of pumping rate

根据式(8)和式(9)，得出基于均值和标准差的敏感度计算结果如式(20)和式(21)所示。

(20)

(21)

3.2 基于二阶矩法的油封可靠性灵敏度计算

根据油封的泵吸率极限状态方程，应用式(11)和式(12)得到μg=1.054 02，σg=0.376，计算得出：β=2.802 26，R=0.997 47。

基于均值和标准差的敏感度结果，分别如式(22)和式(23)所示。

(22)

(23)

3.3 2种可靠性灵敏度方法计算结果比较

图4所示为二阶矩法和蒙特卡洛法的均值灵敏度柱状图，显然2种不同算法得到的灵敏度变化趋势大致相同。油侧唇角、空气侧唇角和过盈量的均值敏感度为正值，理论接触宽度和腰厚的均值敏感度为负值，表明随着油侧唇角、空气侧唇角和过盈量的增加系统可靠度也会增加，反之增加理论接触宽度和腰厚会降低系统可靠度；而且，相对于油侧唇角、空气侧唇角和腰厚，理论接触宽度和过盈量值的变化对可靠度的影响更大，影响程度大小顺序为：理论接触宽度>过盈量>腰厚>空气侧唇角>油侧唇角。

图4 2种算法的均值灵敏度和结构参数贡献Fig.4 Mean sensitivity and structural parameter contribution of the two algorithms：(a)Monte Carlo method；(b)the second order moment method

图5分别为二阶矩法和蒙特卡洛法的标准差灵敏度柱状图，很明显，5个参数的标准差敏感度均为负值，表示增加参数的标准差会降低系统的可靠度，而且理论接触宽度、过盈量和腰厚的标准差对标准差敏感度的影响最大，影响程度大小顺序为：过盈量>理论接触宽度>腰厚>油侧唇角>空气侧唇角。

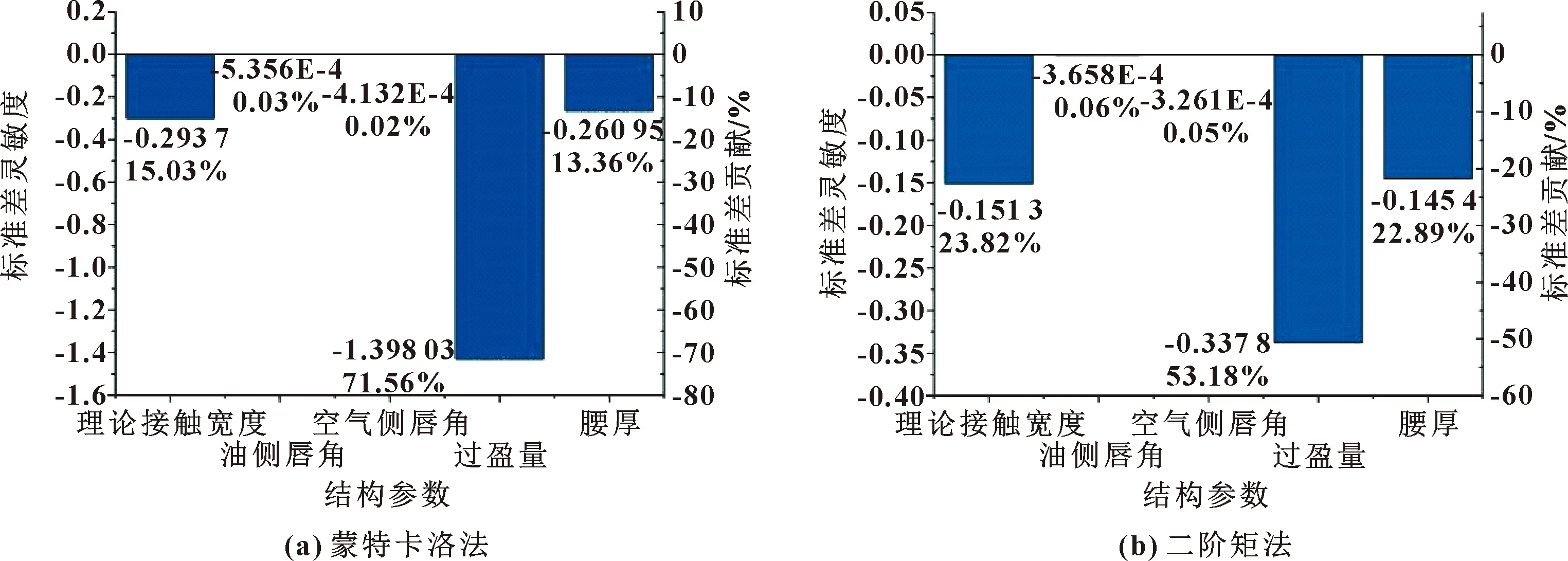
图5 2种算法的标准差灵敏度和结构参数贡献Fig.5 Standard deviation sensitivity and structural parameter contribution of the two algorithms：(a)Monte Carlo method；(b)the second order moment method

图6—10所示为2种可靠性灵敏度计算方法得到的不同结构参数值对油封可靠性的影响程度和趋势。

图6 理论接触宽度对可靠度的影响Fig.6 Effect of theoretical contact width on reliability

图7 油侧唇角对可靠度的影响Fig.7 Effect of oil side lip angle on reliability

图9 过盈量对可靠度的影响Fig.9 Influence of interference on reliability

图10 腰厚对可靠度的影响Fig.10 Influence of waist thickness on reliability

由图6—10可见，2种计算方法计算的各结构参数对油封可靠度的影响趋势相似，数值相差不大。随着油侧唇角、空气侧唇角的增大，油封的密封可靠度提高；随着理论接触宽度和腰厚的增大，油封的密封可靠度降低。

4 结论

(1)运用正交试验法和曲面响应法，将油封的理论接触宽度、油侧唇角、空气侧唇角、过盈量和腰厚5个结构参数作为因子，泵吸率作为响应值，分析计算了拟合极限方程并建立了可靠性模型。

(2)运用二阶矩法和蒙特卡洛法分析旋转唇密封结构参数对可靠度概率的均值和标准差灵敏度。结果表明，2种算法的均值灵敏度和标准差灵敏度大体变化趋势相同，因此算法有一定有效性。

(3)敏感度计算结果表明，增加油侧唇角、空气侧唇角和过盈量时，油封的密封可靠度会增加，增加理论接触宽度和腰厚时，会降低油封的密封可靠度，理论接触宽度的值对可靠度的影响最大；增加5种结构参数的标准差都会降低油封的可靠度，过盈量的标准差对可靠度的影响最大。

(4)文中在探讨给定工况下结构参数对可靠性的灵敏度时，未考虑老化、温度等因素的影响，分析具有一定局限性，在后续研究中将继续讨论。文中研究所用的方法具有通用性，也为其他油封的研究提供了参考。