融合课程思政的深度学习教学案例

【摘要】课程思政指以构建全员、全程、全课程育人格局的形式将各类课程与思想政治理论课同向同行，形成协同效应，把“立德树人”作为教育的根本任务的一种综合教育理念，是目前教学改革的热门话题.文章构建了基于混合式教学的深度学习模型.该模型具有两个创新点：一个是在教学过程中融入课程思政，另一个是激发学生的高阶思维.通过一个无穷级数的具体教学案例，具体分析了如何在线下的教学过程中，将课程思政元素融入教学过程中，发挥教师在课程思政中的主导作用，以及如何一步一步地激发学生的高阶思维，提高教学质量.

【关键词】课程思政；深度学习；无穷级数

【基金项目】温州医科大学教学改革项目“基于混合式学习的深度学习模式”（JG2020077）；浙江省普通本科高校“十四五”教学改革项目《基于“新工科”理念的高等数学教学改革》（jg20220360）

引 言

2020年9月1日出版的第17期《奋斗》杂志发表了习近平总书记的重要文章《思政课是落实立德树人根本任务的关键课程》，文章指出，办好思政课关键在教师，教师要给学生心灵埋下真善美的种子，引导学生扣好人生第一粒扣子，教师要有与时俱进的新思维，要用辩证唯物主义和历史唯物主义将家国、仁爱融入课堂教学中，春风化雨，润物细无声地进入课堂实践中.一方面，高等数学一般分上、下两个学期，师生的情感比较深厚，因此高等数学在高校的课程思政上是有优势的.另一方面，高等数学是一门培养学生能力和提高学生素质的重要课程，它不仅为学生学习后续课程提供必要的知识和方法，而且更重要的是通过数学学习来训练学生的思维能力，提高学生的科学与技术修养，为从事所学专业相关工作和进行深入学习打下坚实的基础.文章以常数项级数的概念来实施融入课程思政的深度学习的教学案例.

一、融合课程思政的教学设计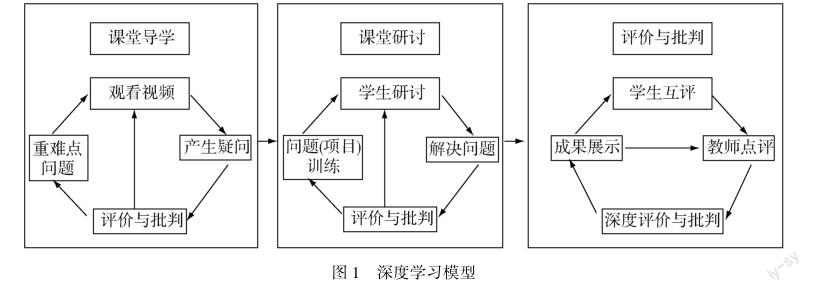

根据图1深度学习模型，设计以下教学过程：

（一）教学背景

学情分析：

优点：大部分学生高等数学的基础知识扎实，上课认真；缺点：大部分学生上课不爱主动提问，需要教师进行引导提问.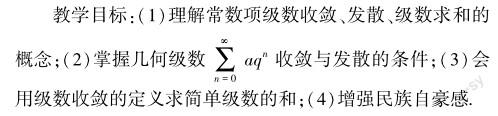

（二）课前导学

教师发布无穷级数预习导读和相关视频，学生通过观看视频和导读，了解本节课的重点———无穷级数的收敛和发散.在这一过程中形成概念性问题：什么是无穷级数，无穷级数是干什么用的.

（三）课中教学

1.引入概念

教师简要介绍无穷级数的发展史：公元前5世纪哲学家芝诺提出了一系列关于运动的不可分性的哲学悖论，如著名的阿喀琉斯追龟问题.接着阿基米德利用归谬法辩论，得到几何级数.中国古代的《庄子·天下》中的“一尺之锤，日取其半，万世不竭”，其实也是关于无穷级数的表述.亚里士多德认识到公比小于1的几何级数可以求出和.到了中世纪，《欧几里得几何问题》明确了几何级数的两种结果.到了17世纪，无穷级数用于函数展开，牛顿和莱布尼茨分别独立得到三角函数的级数展开.17世纪末18世纪初，无穷级数在航海、天文学和地质学领域得到发展应用，特别是泰勒提出了泰勒级数，被数学家广泛地应用和研究.但是这个时期的数学家只是在意无穷级数表示函数和数值计算中的应用.而忽略了它的本质———收敛性.只有莱布里尼茨给出了交错项级数的判别法.18世纪，德国数学家高斯第一次对无穷级数进行了严格的研究，法国数学家柯西是第一个以极限为基础对无穷级数的敛散性建立起完整的理论的数学家，1821年他在《分析教程》中给出了判别无穷级数收敛发散的一些常用方法，如根式判别法、对数判别法.后来由魏尔斯特拉斯提出的一致收敛完成了整个级数理论的构建.但是对于无穷级数的研究工作停止了吗？没有，现在根据实际需要我们的研究工作现在从一维推广到多维，从实数的研究推广到四元数的研究.

思政内容：教师通过讲述级数的发展历史，激发学生勇于探索和实践的精神.并感受数学家们追求科学过程中“路漫漫其修远兮，吾将上下而求索”的艰辛，激发学生不畏艰难追求科学的信心.

2.创设问题情境：利用芝诺悖论进行启发式学习

例2 NBA联赛中纽约尼克斯引进球员帕特里克·尤因，开出10年期的合同，價值为3000万美元，在这10年之中，每年应付300万美元，但是球队老板不会在签约当天支付全额，若年利率为5%，一年计一次复利，假设他分10次支付，每次付300万美元，第一次在签约当天付款，之后每年度末支付一次，问这笔合同的现时值是多少？

设计想法：两道题目都是实际生活中的例子，和学生的生活是有关系的，一方面提高了学生对无穷级数的学习兴趣，了解级数在实际生活中的重要作用和应用，让同学们觉得这个东西是在生活中有用的，提高学生运用级数处理实际问题的能力.另一方面使学生也学会对事物进行抽象概括的学习，掌握深度学习中的迁移学习的能力.

（四）课后评价

学生完成教师线上布置的作业，并相互评价各自的学习成果，在知己知彼中，了解自己的学习成效，以及自己在班级中的学习排名，激发学生的学习积极性和胜负欲，在友好的竞争环境中，激发各自的学习潜能，以达到互相监督，互相进步.

结 语

在教学过程中，让学生了解无穷级数的历史，对为无穷级数做出贡献的数学家产生敬佩，达到课程思政的目的.同时，课前、课中、课后的合理安排，让学生进行沉浸式学习，达到深度学习的目的.

【参考文献】

[1]习近平.思政课是落实立德树人根本任务的关键课程[J].奋斗，2020（17）：4-16.

[2]胡晓晓.基于翻转课堂的深度学习模式研究[J].教育现代化，2019（16）：158-160.

[3]C.H.爱德华.微积分发展史[M]，北京：北京出版社，1987.

[4]潘文杰.傅里叶分析及其应用[M]，北京：北京大学出版社，2002.