大概念统摄下的学科项目化学习

王希

［摘 要］唯有经历贴近真实的、主动探究的、创造式的活动，学生才能深入数学知识脉络，深刻把握知识内核。项目化学习基于学科大概念，以项目或者任务为载体，驱动学生在问题情境中自主开展实践性学习活动，自主构建知识结构框架，为解决学习碎片化现象提供了合适的方法导向，便于学生真正领会知识本质和应用数学知识，融通数学思维和技能。

［关键词］项目化学习；大概念；核心素养；小学数学

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2023）20-0048-04

项目化学习（PBL）是基于学科核心概念，以项目或者任务为载体，驱动学生在问题情境中自主开展实践性学习活动。项目化学习可以融通数学思维与技能，那么如何以项目任务的形式，引导学生形成整体性的结构化认知，明确概念本质？这就要求教师熟知学科整体结构中的大概念，围绕知识核心进行教学目标的重构，设计活动项目，再将项目内容付诸实践。下面，笔者以“两位数的再认识”为例进行具体说明。

一、在领域结构中厘定大概念

将学习内容置于学科相应的领域结构中审视，明确其在知识系统中的地位和作用，提炼出能反映知识整体的本质核心及内在关系的概念，或具有广泛的适用性和解释力，以及具有概括迁移价值的原理、思想或方法，这些即为大概念。

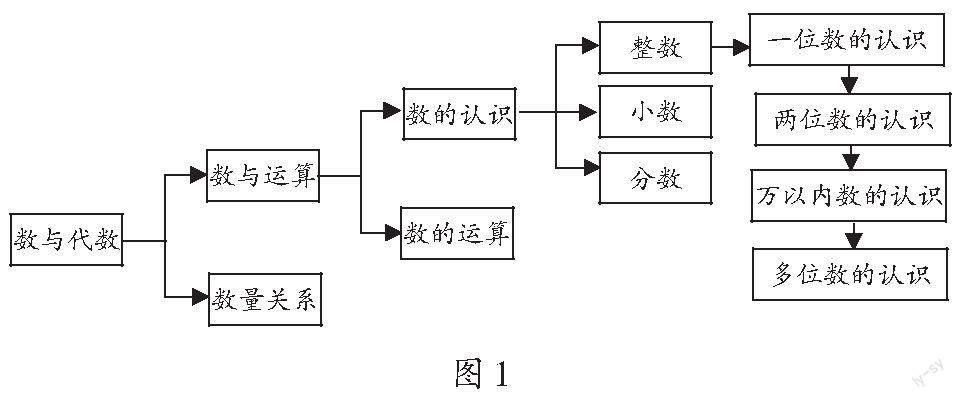
小学阶段“数与代数”领域包含“数与运算”“数量关系”两大主题（如图1）。课程标准强调，量之间的关系表达离不开数与运算，而数与运算均要以计数单位为核心予以统领。“数的认识”中，从整数到小数、分数，都是由数量到数的抽象过程，核心概念就是用抽象符号表达数的意义。其中，整数具体表达为“十进位值制计数法”，用0～9这10个数，以及十进制、位值制的计数规则，就能表征任意对象的数量。这是计数单位在整数中的表现形式，小数和分数的表达也是类似的抽象方式。“数与运算”中，算理、算法的理解最终也要追溯到计数单位对数义的表达，具有一致性。因此，“十进位值制计数法”可以看作是一套完整的符号表征系统，是统摄整数的大概念，能真正凸显数的本义，也是“数与代数”领域结构中的主要线索之一。

二、在知识主线中整合核心内容

根据数学教材编排的相关内容顺序，整数的教学主要包含认识10以內的数、认识11～20各数、认识100以内的数、认识万以内的数、认识多位数。0～9的认识是让学生初步体会运用符号表示数量，培养符号意识；在苏教版和人教版教材中，“10的认识”是独立课时，让学生初步感受数从量变到质变的转折，具有开启体会十进位值制意义的基础地位；100以内数的认识是数的表征开始构建成形；万以内数和多位数的认识是对十进位值制计数法的拓展延伸，培养学生知识迁移应用的能力。可见，两位数的再认识是统领知识主线的关键内容，也是培养学生迁移计数能力的基石。

三、在概念维度下确定项目目标

好的项目设计，需要依据大概念的具体维度对学习目标进行设计。

首先，要将大概念蕴含在设计的问题之中，形成项目实践目标，以及要能从项目中提炼出知识结构的核心问题。

其次，学生能以数学的眼光理解任务内容，用数学的思维思考项目的核心本质，用数学的语言表达对项目的理解，用适合的数学工具解决问题。

最后，在项目交流中，学生能正确评价自己和别人的项目成果，应用核心知识转化为评价依据，在评价总结过程中感知知识的价值所在。

在大概念具体化维度的引领下，项目设计以“在计数从量到质的转变中体会十进位值制计数法的原理，能基于计数规则创造符号来表征数量”为出发点，设计详细的项目实践目标（见表1），将认识10、认识11～20各数、认识100以内的数整合起来，重构成跨学期的学习项目——“两位数的再认识”。

四、在目标指导下实施具体任务

项目化学习相比常规的课堂探究活动有着特别的优势，它不仅能突破教材中课时分散的限制，围绕大概念将两位数的内容整合起来教学，还能突破时空限制，设计成“课前+课中+课后”“校内+校外”的长程活动，为学习的实施提供便利。因此，根据项目实践的具体目标，可在不同时间段设置相应的项目任务，渗透核心素养的培养（见表1），为学生形成扎实的结构思维做铺垫。以下是具体实施过程。

1.应用原理，合作创造

弗赖登塔尔认为，学习数学唯一正确的方法是进行再创造，即由学生本人把要学习的东西发现或创造出来。显然，“做数学”本身也是数学学习的目的。经历“再创造”的过程，能使学生在参与问题解决的过程中体悟核心概念，建构属于自己的认知结构。

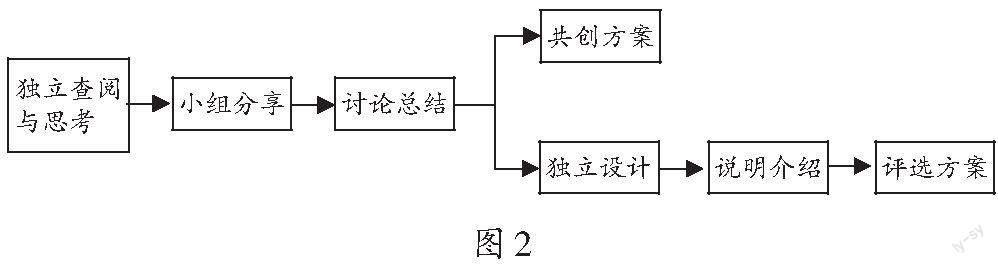
如图2所示，通过自主阅读和思考，强化了对计数原理的认知后，小组成员需要聚集在一起分享自己的想法和收获。有的小组在思维的碰撞和纠偏中，有条理地总结两位数创造的要点，讨论出理想的创造方案。有的小组会选择在讨论后每个成员出一套方案，然后由每个人说明设计理念和优势所在，再共同评选出大家一致认可的方案。其中，每一步的分享、讨论与筛选，都是培养学生用语言表达思维最自然、最有趣的方式。

对于设计方案的创造与改进，不同小组的呈现结果必然会有层次差异，这样的差异会反映到项目成果中。因此，教师要提前收集各小组方案，进行初步的分类和筛选，目的有两点：一是课堂上需要有典型案例的分享，以及代表性资源的对比评价；二是精选部分作品适应课时容量，尽量围绕核心目标展开研讨，做到课堂的提质增效。图3是笔者整理的部分设计作品，包含失败的、有待改进的和比较成功的代表类型。其中，方案1每个数字都用一个新的符号表示；方案2是将算筹的纵式和横式交换了位置；方案3～5分别使用了字母、文字、图形的不同方式表征两位数。

2.介绍推广，以教促学

能促使学生加深记忆、灵活应用的方法就是把知识教给别人让别人探索，进行项目推广本质上也是以教促学的一种变式。

在设计方案定型后，小组两人之间需要把自己创造的两位数介绍给对方，在有限的时间内教会对方自己新创的两位数，并让对方说出计数规则与组合原理。让他人了解、接受、喜欢上自己创造的事物，能大大激发学生的兴趣和热情。

在这个过程中，教师应参与其中并进行帮助和指导。为了不打击部分学生的信心，也为了学生能更好地理解计数法，可以及时给予失败小组帮助，提供整改的机会。整改方案的前后对比是项目实践中宝贵的生成性资源，它体现的是学生对知识的认知从浅表到本质的转变过程，也能更加动态地展现设计原理的合理性，极具研讨价值。

3.课堂研讨，项目反馈

项目化学习的主要特征除了“做中学”“用中学”“创中学”，还有作品化。教与学都围绕着作品的生成，按有形的任务线索展开，关注显性素材的准备和使用。成果产生的过程也是学习结果在物化作品中的界定。

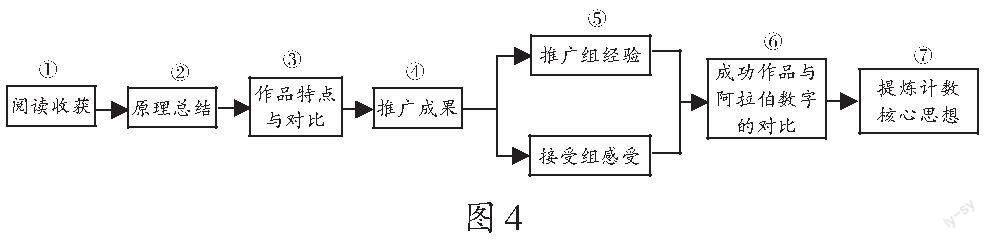
“两位数的再认识”的项目成果包含两部分，一是两位数的创造方案，二是设计推广成效。课堂中，教师要围绕这两点设计研讨、反馈的流程（如图4），每个流程须紧扣实践目标和项目环节，以大问题展开，即以提问的形式复盘作品产生的过程，引导学生思考互动，生成要点，提炼知识核心思想。

流程①是资料阅读的反馈。

问题：根据我国数字发展史，你认为古人是怎么设计两位数的？这样的设计好在哪里？为你们小组两位数的创造提供了怎样的经验？

[经验举例]

①古人最开始用手指数的时候数到10不够数了，对数字继续地创造产生了影响。

②无论是用绳结、算筹还是阿拉伯数字记数，都习惯10个符号为一组进行组合变化。

③算筹和阿拉伯数字中，不同数位上的符号一样时，表示的数量不一样。

流程②是计数原理的讨论。

问题：你们小组认为设计两位数的关键要点是什么？

[要点举例]

①两位数的组成是有规律的，个位每满10，十位上就会增加1。

②不同数位上的数表示的意义不同。

③ 需要一些基础符号才能组成不同的两位数。

流程③是作品的展示與分析。

问题：每样作品有什么特点？对照设计关键要点说说好（或不好）在哪里？不同的作品之间有什么异同，产生了什么影响？

[分析举例]

①方案1设计的每个符号都不相同，有一个数就创造一个符号来与之匹配，那么无穷的数就要创造无穷的符号来表示，造成了创造和使用的困难。

②方案2是改编的算筹计数法，需要用到横纵两组数，比较烦琐，不像方案3和方案4，只要记住10个符号就能表征所有两位数。

③几组成功的方案为了计数的简便，都改变了0～9的表征符号，说明创造两位数的前提是创造必要的基础符号。个位只要满10就需进1，相同的符号“几”在十位上就表示“几十”。

④方案3的表征符号特别简洁，跟阿拉伯数字一样都是1或2笔写成，而且是熟悉的拼音。

流程④是推广成果的分析。

问题：成功推广的小组是如何迅速教会他人默写新的两位数的？接受组为何能快速接受并学会？推广失败的小组失败的原因是什么？

过程：推广组与接受组结合计数法解说，最后全班共同讨论。

流程⑤是回归对已学两位数的分析。

问题：这些成功的创新数与我们学习的两位数有什么相同之处？挑出你最喜欢的，说说理由。你对我们学习的两位数有了什么新的认识？

生成：制订表征两位数优劣的判断标准。

流程⑥是计数核心思想的深度提炼。

问题：经历了两位数再认识的项目过程，你有何反思？（结合作品谈谈改进意见和原理）你能继续设计三位数吗？

流程⑤和流程⑥的对比反思过程，其实都是对计数三要素的再次总结和细化。至此，当再回答前文的问题“为什么0～9都是一个数字，从10开始就要用两个数字构成？”时，学生已然胸有成竹，甚至迁移到多位数也不成问题。因为在做项目的过程中，数字这套表征系统的核心概念已经渗透到了他们的思维里。

项目化学习的成果往往是多元而深入本质的。基于课程标准的知识大概念，明确了开放性项目设计的方向，使学生能在实践中呈现丰富的、多层面的解决方案，并不断地在讨论中畅通思路、优化方案。教师在项目推进中注重探索过程的思考，追问以问题“为何有的方案更优”“怎样使方案更优”深入，系统地推动学生研讨、迭代和反思。双方共同促进了探究性实践活动的真正落地。

4.评价优化，成果展示

对项目成果的评价主要聚焦于项目过程和作品，但评价形式、维度和时机可以是多样的。以课中研讨流程为例，流程③和流程④为生生互评，教师对各环节的总结和提示即为隐性的他评。课后可将优秀成果、特色成果、优化成果、拓展成果予以分类展评，促进小组间的互相学习，鼓励拓展新研究。其中，评价维度与项目过程一脉相承，包括参与程度、各流程贡献、学生对问题的理解与思考、语言表达的适切性、成果的合理性等多个方面，重在运用发展性评价，选出单项和综合表现之星。最终，用教、学、评的一致性有效推动学生的数学知识、技能、思维协同发展，让数学核心素养落地。

综上，项目化学习顶层的大概念和具体项目内容，是学科项目化设计的重要组成部分，具有立足学科领域整体，建构和迁移数学知识的独特价值。利用项目化学习，以及利用探索知识本质的设计和实践整合碎片化教学内容，对教学来说是一种启发性尝试，也是培养学生核心素养的一种方式。