圆锥曲线中两类定值问题的等价刻画
2023-09-28重庆市铜梁二中402560
中学数学研究(江西) 2023年10期
重庆市铜梁二中 (402560) 李 波
文[1]考察了圆锥曲线的一个定点问题:在圆锥曲线Γ上任取一点P,过P作两条斜率分别为k1,k2的直线l1,l2,且l1,l2交Γ于A,B两点,若k1+k2(或k1k2)为定值,直线AB是否过定点?本文将探究两类类似的定值问题,并给出等价刻画.

图1
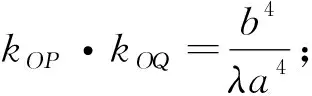
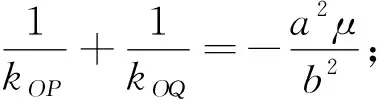




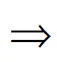

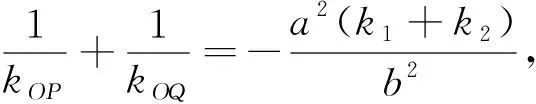


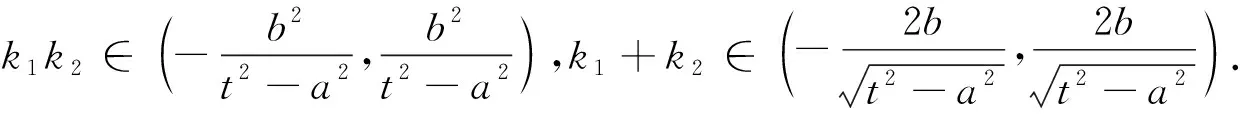
双曲线和圆上有与性质1完全类似的结论,即
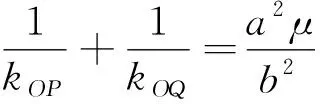
性质3 过点F(t,0)(t≠0)的两条不同直线l1,l2交圆E:x2+y2=r2(r>0)所得的两弦AB,CD的中点分别为P,Q,k1,k2分别是l1,l2的斜率,则
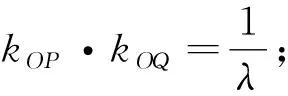

抛物线上的情况略有不同,即
性质4 过点F(t,0)(t≠0)的两条不同直线l1,l2交抛物线E:y2=2px(p>0)所得的两弦的中点分别为P,Q,k1,k2分别是l1,l2的斜率,则


