“套路”诚然好 “通法”价更高

安徽省合肥市第六中学 (230001) 王 其

一、问题提出

在数学学习中,对于典型的问题往往都有特殊的处理方法,即固化的解答套路,如在排列组合问题的处理中,相邻的问题计数用“捆绑法”,不相邻问题计数用“插空法”比较方便,但这些特殊的方法只适用于特殊的试题情境,故并不是通性通法,但是根据辩证法“普遍性寓于特殊性之中”的原理知,解题套路必然来源于“通性通法”,其实,“通性通法”不仅是“套路”的来源,而且也是培育学生核心素养的生长点,然而,教学中发现,教师在处理典型的问题时,往往仅仅注重“解题套路”的应用,而忽视支撑“解题套路”背后的“通性通法”的掌握,不利于核心素养的达成,所以教学中不仅仅要介绍套路,更重要的是要揭示“套路”背后的“通性通法”.

二、案例展示

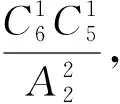
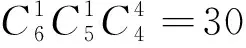
三、教学启示

诚然,学习数学是需要“刷题”,如果不刷题,谁也学不好数学,正因为这个逻辑关系,“刷题”俨然成为了学习数学的代名词,于是乎,“忽视原理的揭示重机械刷题”的教学模式大行其道至今,教师教学表现为将同一类型的问题用什么方法整理得头头是道,让学生照猫画虎去套用,例如,案例中的平均分组的问题,如何将“有序”分组化为“无序”分组的套路,教学中如何教师引导学生总是沉浸在“套路”之中去处理计数问题,这种学习方式就是机械刷题,因为机械套用这法那法,缺乏思维灵活性,则学生就觉得这一章难学,因为不少题目的处理是没有套路的,需要学生有深度思考的能力,而深度思考的能力来源于通性通法的理解与掌握.当然,并不是说“套路”一定不好,其实,对于套路化的题目,用“套路”十分快捷,只不过,如果数学学习一味追求“套路化”,大脑就会僵化,缺乏宏观的策略引领,学生见木不见林.

事实上,解决计数问题的两个原理,是处理计数问题的根本方法,其中分类加法计数原理是分类讨论思想的具体体现,而分步乘法计数原理与分类加法计数原理息息相关,它是分类加法计数原理的进一步优化,基于此认识,可以说,分类讨论思想是处理计数问题的通性通法,是灵魂所在,故分类讨论思想也是此类解决问题的方向,虽然面对套路化的题目,诚然采用“套路”更快捷,但毕竟使用范围有限,但是“通性通法”具有一般性,其价值更高.