二次函数复习的“一题一课”聚焦

⦿山东省平邑县白彦镇第二初级中学 李 伟

二次函数是初中数学综合题的重要载体,是知识、方法与思想的结合体.在复习中,要善于抓住典型例题,突出“一题一课”复习模式,通过一题多解,培养学生发散思维,达到解一题通一类,即触类旁通的学习境界,跳出问题学数学,让学生站在更高的角度去深层探究,在探究中获得愉悦的数学体验,从而提升数学核心素养,生成数学解题智慧[1].

1 原题呈现

如图1,抛物线y=ax2+bx-3的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,直线l与抛物线交于点B,交y轴于点D(0,3).

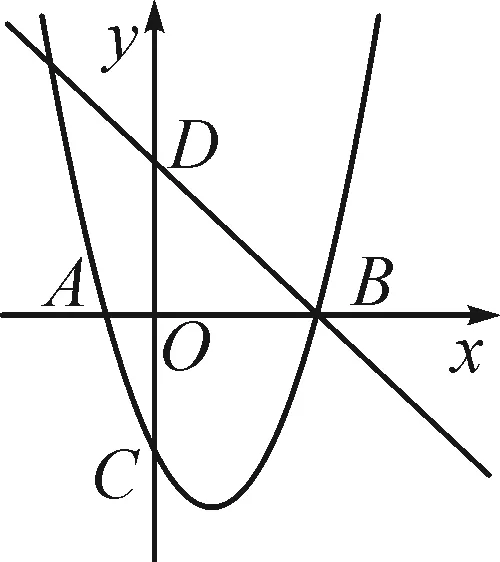
备用图

图1

(1)求该抛物线的函数表达式;

(2)点P(m,0)为线段OB上一动点,过点P作x轴的垂线EF,分别交抛物线与直线l于点E,F,连接CE,CF,BE,求四边形CEBF面积的最大值及此时m的值;

(3)点M为y轴右侧抛物线上一动点,过点M作直线MN∥AC交直线l于点N,是否存在点M,使以A,C,M,N四点为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.

2 透过解题,积累策略

2.1挖潜待定系数法的内涵

第(1)问的解答如下.

2.1.1 一般式

所以,该抛物线的函数表达式为y=x2-2x-3.

2.1.2 交点式

根据题意,设函数解析式为y=a(x+1)(x-3),所以-3a=-3,解得a=1.所以,该抛物线的函数表达式为y=(x+1)(x-3),即y=x2-2x-3.

2.1.3 顶点式

2.1.4 韦达定理式

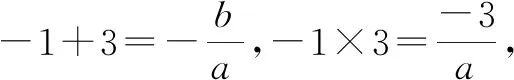
2.2 学会一种方法,巩固配方法求最值

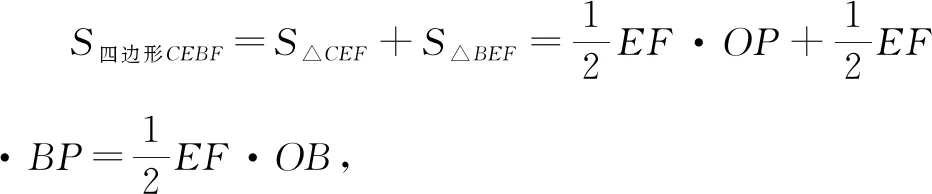
2.3 学会探索二次函数存在性问题

第(3)问的解答如下.

解法1：存在.理由如下.

①当点M在直线BD的下方时,如图2,由题意得OC=3,OA=1.过点M作y轴的垂线,垂足为E,过点N作NF⊥ME于点F,交x轴于点G.假设四边形ACMN为平行四边形,则AC∥MN,AC=MN.因为NF⊥ME,ME⊥OE,所以NF∥OE,∠ACO=∠MNF.

图2

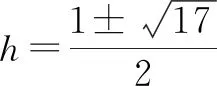
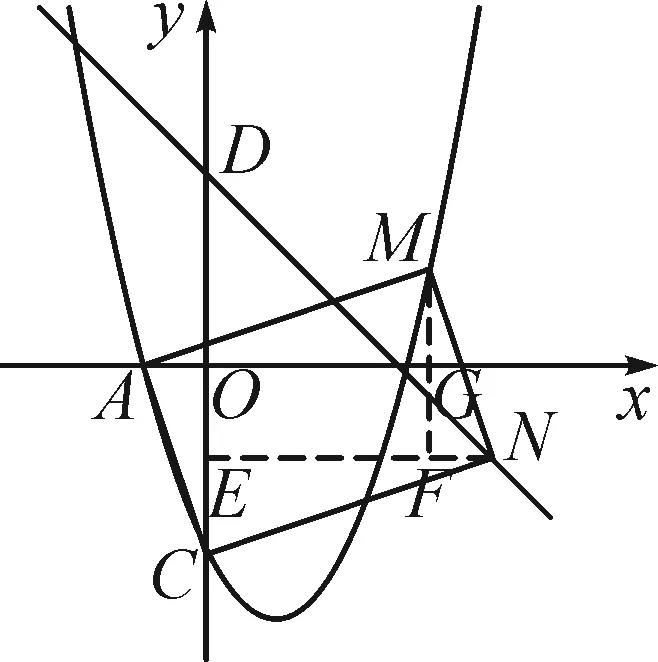
图3

解法2：存在.理由如下.

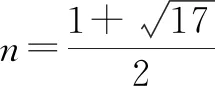
点评：存在性问题是二次函数中创新题型的特征之一,解答时,先回答存在还是不存在,后根据条件解答.对于平行四边形的存在性问题,解答时,要把握好几个关键点.

(1)平行四边形的对边平行,转化为代数式语言就是对边直线的“k”值相等.

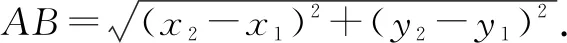
(3)合理进行图形的分割,灵活选用三角形全等作为解题工具也是一种很有效的解题方法.

3 结束语

二次函数的重要性已经不言而喻,三段式问题模式已经趋于稳定,开放的是知识点,是问题提出的视角、探索结论的途径,以及生成不同的新结论.面对成熟的问题结构,如何提高复习效率,确保学生遇到此类问题至少能顺利破解前二问,努力争取第三问,还需要多思考,多探索,多尝试.只有教师站在深刻解题的新高度,才能给学生带来全面解题的新体验,才能更好地激励、引导学生学好数学,克服畏难情绪,增加数学学习的自信心,提高数学解题智慧,提升数学核心素养.