基于FD-AT-LSTM的大型风电机组变频器温度状态监测

2023-09-26胡耀宗陈修高董得志孙晓彦

动力工程学报 2023年9期

胡阳, 胡耀宗, 程逸, 陈修高, 董得志, 孙晓彦

(1.新能源电力系统国家重点实验室,北京 102206; 2．华北电力大学控制与计算机工程学院,北京 102206;3．国家电投集团科学技术研究院有限公司,北京 102206)

随着碳达峰、碳中和目标的不断推进,大型风电机组在节能减排过程中起着越来越重要的作用。变频器是风电机组的关键设备,其主要功能包括:(1) 在给定的转速范围内将发电机输出的电能反馈给电网;(2) 产生系统为建立交变磁场和感应磁通所需要的无功功率;(3) 在风电机组或电网故障时,变频器启动保护动作。变频器一般在外部环境中工作,环境温差大、油污侵蚀等原因可能会使其性能受到损害,严重时会引起变频器故障。因此,风电机组变频器的状态监测[1]对于风电机组的健康状况极其重要。

传统的风电机组关键部件状态监测与故障预警方法主要有决策树[2]、随机森林[3]、支持向量回归[4]、XGBoost[5]、LightGBM[6]和神经网络[7]等。孟宪梁等[8]通过分析数据采集与监视[12](Supervisory control and data acquisition, SCADA)系统数据,使用风速、转子转速等24个传感器的参数作为机器学习模型的输入,以变桨系统变频器的温度作为机器学习模型的输出。通过对比XGBoost和LightGBM 2种机器学习方法的模型评价指标判断其在变桨系统变频器状态监测上的优劣,使用基于滑动时间窗残差估计方法对变频器故障进行预测。结果表明,相对于LightGBM算法,XGBoost算法对变桨系统变频器的故障预警方法更简便、结果可靠,更适用于风电机组变桨系统故障预警。刘冰冰等[9]提出了一种随机森林算法对变频器的故障进行检测,在SCADA中的环境参数、控制参数、电气参数和状态参数中取出故障、停机、维修和限功率等非正常发电状态下的数据建立变频器故障检测模型。结果表明,用随机森林算法进行故障诊断,准确率高,但在实际工程中实现起来比较困难。胡立锦[10]对变频器故障类型及故障原理进行了仿真分析,得到不同故障状态下直驱式风力发电机的输出电压及波形变化情况。将仿真结果经处理后作为数据样本对设计好的神经网络进行训练和测试,使神经网络具有诊断和故障定位的能力。Yahyaoui等[11]利用主成分分析法对风电机组SCADA中的扭矩、发电机转速、电网电流和输出电压等12类数据进行特征提取,并用不同的机器学习方法进行状态监测。通过分析风机不同工况下的仿真数据,验证了该方法的有效性和较高的分类精度。

变频系统是风电机组发生故障的主要部位,其故障比较常见,维护工作量大,维修较难,对变频器的合理监测可以减少维护维修过程中的人力物力损失,因此,笔者提出了大型风电机组变频器状态监测及分析方法。首先,基于风电机组变频器工作原理,分析SCADA中变频器的监测参数,筛选出了适合风电机组变频器的输入、输出参数。然后,对所采集到的监测原始数据分析数据的特征,设计了数据的预处理流程。随后,基于赤池信息准则(Akaike information criterion, AIC),引入有限差分回归向量作为有限差分(Finate difference, FD)-注意力机制(Attention, AT)-长短期记忆(Long shortterm memory, LSTM)神经网络模型输入,即FD-AT-LSTM模型,建立了变频器状态监测模型,并采用带有故障数据的样本进行验证,证明了该方法的有效性。

1 变频器工作原理及其监测参数

风力发电系统变频器应用最多的是双馈式、笼型异步式和直驱式3种,除了笼型异步式,其他2种必须经过变频处理后才能接入电网中。变频器主要由整流(交流变直流)、滤波、逆变(直流变交流)、制动单元、驱动单元、检测单元和微处理单元等组成,图1和图2分别为永磁直驱风电系统和双馈风电系统的结构示意图。

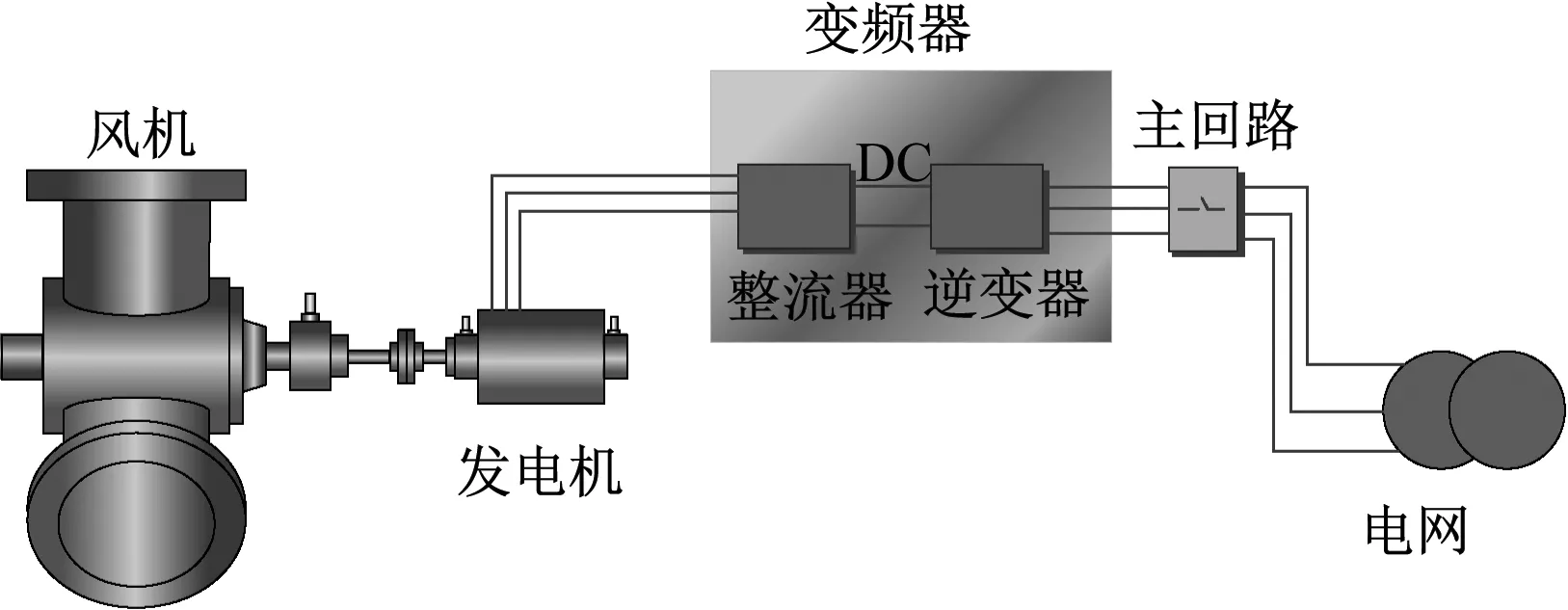
图1 永磁直驱风电系统示意图

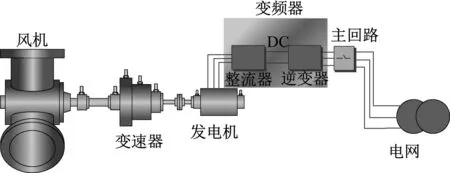
图2 双馈风电系统示意图

双馈式风电机组风机转轮与发电机转子之间通过变速器相连,而直驱式风电机组风机转轮与发电机转子直接相连。由于风电机组运行时工况多变,发电机产生的电能不是稳定的50 Hz,因此需要变频器将发电机产生的电能经过处理后并入电网中。发电机产生的电能首先经过转子侧的变流器,也称整流器,将发电机产生的交流电变成直流电,经过整流器的直流电随后经过直流斩波器变成固定可调电压的直流电。最后经过网侧的变流器也称逆变器,将直流电变成稳定频率的电能,电能经过交-直-交的变换成为稳定频率的电能输送到电网中。

从变频器前后的结构可以看出,变频器的运行不仅与自身参数有关,还与风轮、发电机和电网的重要参数有关。风电场运行中负责对场区内所有风力发电机组的运行状态进行实时监控、对机组的各个子部件参数进行信息采集和储存的系统称为SCADA系统[12],该系统能够针对发现的异常状态或者故障状态,及时主动发出声光报警,以便风电场运维人员能够及时响应。合理选择SCADA中的关键参数对构建风电机组关键部件的状态监测模型十分重要。

变频器的主要部件是变频器内部的绝缘栅双极型晶体管(IGBT)以及电网侧和机组侧的变流器。整流器和逆变器的工作机理均是通过调整IGBT的开断来调整输出电源的电压和频率。IGBT是变频器中的重要结构,其状态与性能直接决定了变频器的运行状态,在风电机组变频器的状态监测中主要考虑IGBT模块的运行状态。因此,选择IGBT模块的相关参数作为表征变频器运行状态的参数指标,能够有效反映变频器的运行状态。选取SCADA系统中有关发电机、变频器和电网的相关参数,初步选定风速风向等20个变量为模型的输入变量,如表1所示。选择变频器IGBT温度作为模型输出变量。

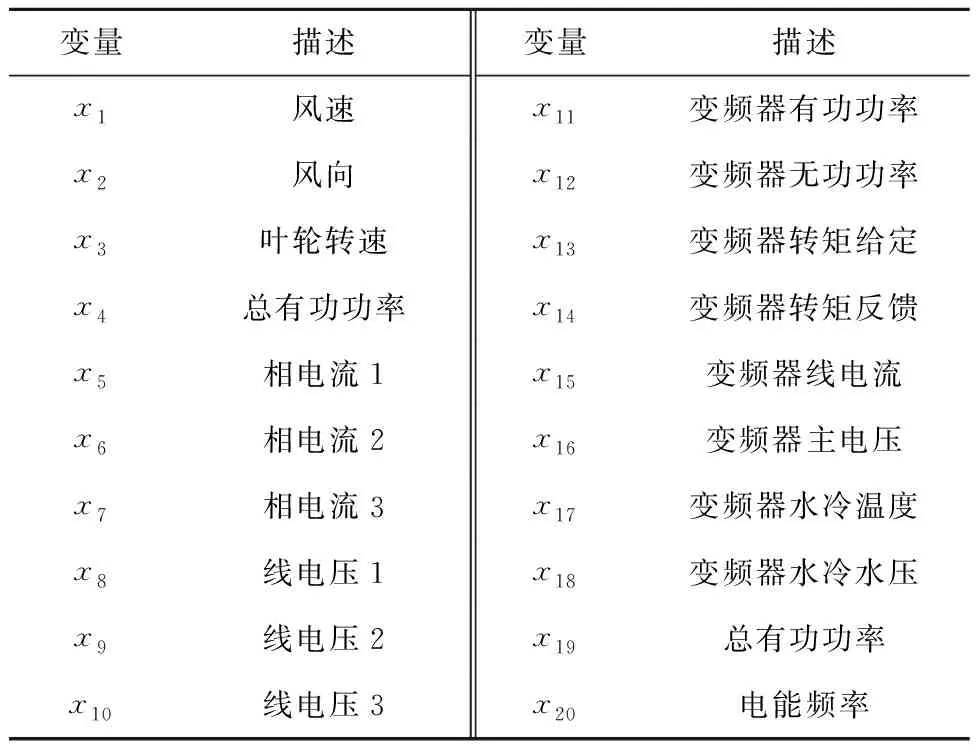
表1 输入变量

2 运行数据预处理

风电机组在运行过程中会产生大量运行数据,以风电机组变频器IGBT温度为研究对象建立模型的过程中,选择哪些运行量作为输入数据、如何对所选择的变量进行处理以提高模型的高精度逼近能力是需要关注的问题。基于此,笔者设计了风电机组变频器状态监测模型建立前的数据预处理流程,主要包括基于随机森林的特征选择以及基于最小均方误差(LMS)自适应滤波的噪声消除。

2.1 基于随机森林的输入特征选择

由于SCADA系统采集到的数据特征较多,若将相关性较小的特征都用来训练会增加模型训练的难度,并且由于非相关特征较多,模型噪声也会增加,因此需要对采集到的风速、风向和叶轮转速等20个变量进行特征提取。

基于随机森林的特征选择方法是一种非线性的特征选择方法,变频器IGBT温度与其他相关变量之间存在明显的非线性关系,因此选择随机森林[13]方法进行特征选择。首先对待选变量进行归一化处理,并将数据集分为训练集和测试集。之后采用回归随机森林方法以待选变量集作为输入,以变频器IGBT温度作为输出,进行基于回归随机森林[14]的输入输出建模。

随机森林回归模型在构建过程中会对每个特征进行基于袋外数据打分,得到的结果作为特征的重要性得分S。S越高,表明该特征在建模过程中的重要程度越高,选取S较高的变量作为特征选择的结果。

假设随机森林中回归树的数目为Ntree,原始数据集有d个特征,单特征Xj(j=1,2,…,d)的基于袋外数据(out of bag,OOB)误差分析的特征重要性度量按如下步骤计算:

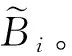
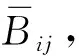
计算所有回归树特征Xj置换前后袋外数据分类误差率的平均变化量:

(1)

2.2 基于LMS自适应滤波的噪声去除

对输入输出变量进行特征选择,能够提高模型精度、降低模型复杂度,同时,对输入输出变量进行噪声去除也是提高模型高精度逼近能力的重要方式。在采集与存储过程中,SCADA中存储的海量风电机组运行数据由于人为因素或自然因素不可避免地会带有噪声。如转轮风速传感器在采集风速信息时会受到通讯干扰,变频器电流电压等电气量数据会受到电磁干扰等,从而产生随机噪声。这些噪声的存在会影响模型精度和预测结果的准确度,因此在训练模型之前需要选择合适的方法消除监测数据中的随机噪声。

LMS变步长自适应滤波方法[15-16]可以去除采集过程中产生的随机噪声,且处理后的数据不失真,数据质量好,可用来直接进行模型建立,因此可对风速、电流和变频器水冷温度等数据进行LMS自适应滤波,自适应滤波器的原理框图如图3所示。其中,W(n)为自适应滤波器在时刻n的权矢量;X(n)为时刻n的输入信号矢量;d(n)为期望输出值;v(n)为干扰信号;e(n)为误差信号;Lf为自适应滤波器的长度。

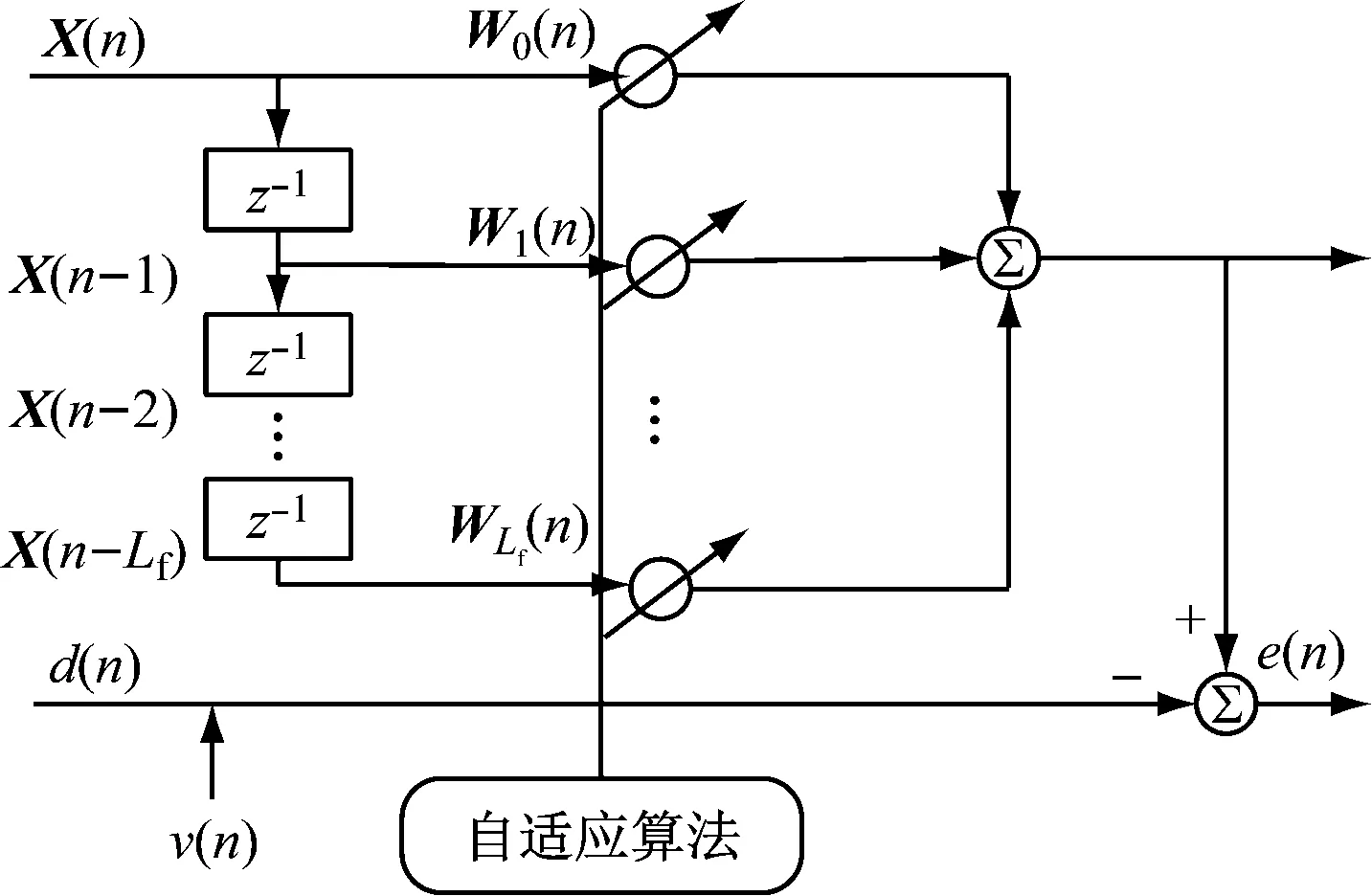
图3 自适应滤波器原理框图

基于最速下降法的LMS算法的迭代公式如下:

e(n)=d(n)-XT(n)W(n)

(2)

W(n+1)=W(n)+2μe(n)X(n)

(3)

式中:μ为步长因子。

LMS算法收敛的条件为:0<μ<1/λmax,其中λmax为自相关矩阵的最大特征值。

3 变频器运行状态监测及分析方法

3.1 有限差分运行域确定

在运行过程中,影响风电机组变频器温度的因素较多,且由于各部件之间的相互作用,当前时刻的温度输出值带有延迟,为了更精准地反映当前时刻温度,需要考虑输入与输出的延迟阶次,构建有限差分回归向量[17]用于变频器运行状态监测。

定义有限差分运行域下的回归向量φ(t),经过有限次差分运算,可得t时刻的变频器温度输出为:

T(t)=f(φ(t))+eF(t)

(4)

式中:T(t)为t时刻变频器IGBT温度;φ(t)为回归向量,由变频器IGBT温度和其余相关变量组成,φ(t)=[T(t-1),…,T(t-n1),x1(t),…,x1(t-n2),…,xq(t),…,xq(t-nm)],其中x1,x2,…,xq为特征选择的q个变量;n1,n2,…,nm为模型阶次;f(·)为有限次差分运算;eF为噪声。

有限差分回归向量中各变量的模型阶次根据赤池信息准则确定,计算结果OAIC的值越小,模型效果越好。其一般形式如下:

(5)

式中:OAIC为根据赤池信息准则计算的结果;lnL为模型的对数似然值;np、mv为模型阶数;Np为观测数目。

3.2 FD-AT-LSTM变频器温度监测模型

3.2.1 AT-LSTM

长短期记忆神经网络[18-21]是一种特殊的循环神经网络(Recurrent Neural Network, RNN),普遍用来解决长序列数据训练过程中出现的梯度消失和梯度爆炸问题[22],与普通的RNN相比,LSTM在较长的序列数据中表现更好[23]。同时LSTM中加入了记忆模块,能够更好地处理长时间序列问题。因此,针对基于时间序列采集的变频器IGBT模块相关监测参数,采用LSTM处理具有较好的效果。

注意力机制[24-27]在模型训练过程中能够识别关键信息并给予更高的权重,对于相关性较低的数据给予低权重或忽视非关键信息,并且在训练过程中不断更新权重,因此鲁棒性高,具有较好的模型性能。

将LSTM与注意力机制结合的模型称为AT-LSTM模型,其将二者的优势互补,既能在长时间序列的数据中更好地训练模型,又能在多输入变量中不断更新权重。

3.2.2 模型结构

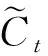
图4 FD-AT-LSTM结构

3.2.3 数据归一化

由于采集到的不同监测变量的取值范围不同,直接将采集到的数据用于模型训练会降低模型精度,在训练之前根据式(6)将所有样本归一化到区间[0,1]。

(6)

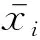
3.2.4 FD-AT-LSTM模型有效性验证

为了有效评价模型精度,引入均方误差eMSE、均方根误差eRMSE和平均绝对误差eMAE3项评价指标,这些指标的计算公式如下:

(7)

(8)

(9)

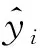
eMSE、eMAE、eRMSE的值越小越好。

3.3 残差处理方法

FD-AT-LSTM模型建立后,需要对残差进行处理来达到状态监测的目的,本节通过处理残差矩阵得到检测指标h,并根据检测指标的阈值判断变频器的运行状态,其计算公式如下。

(10)

得到残差序列E后计算残差矩阵的均方误差eMSE。

(11)

由均方误差以及残差矩阵可得到检测指标h:

h=E-eMSE

(12)

计算完成后,需根据检测指标h的分布确定检测阈值d。对得到的检测指标采用核密度估计的方法得到h的概率密度函数,再根据概率密度函数确定检测阈值d。

对于样本h={h1,h2,…,hN},N为样本数,采用核密度估计计算概率密度p(h)如下:

(13)

其中,σ为核函数带宽系数,K(·)为核函数。使用高斯核作为其核函数,高斯核表达式如下:

(14)

式中:g为2个数据点间的欧氏距离。

最后根据计算得到的概率密度分布,由式(15)计算得到检测阈值d,其中α为置信水平。

2.充分调动职工参政议政的积极性，促进各项决策更趋向科学化。一号煤矿通过厂务公开，把发展、安全、经营的重大事项通过职代会等多种形式如实地向广大职工报告，诚心征求职工意见，极大程度地调动了职工的积极性与创造性，统筹宏观层面与微观层面，发挥集体智慧，促进各项决策趋向民主化与科学化，激发职工爱厂敬业的热情。近几年，一号煤矿在实际运行中多次采纳职工合理化建议，以激励激发职工参政议政的积极性，职工主人翁意识显著增强，创造了数目可观的经济效益，多项科技成果得到不同级别的认可并广泛推广。

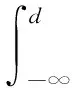
(15)

检测阈值确定以后,根据实际应用场景中所得到的检测指标是否处于置信区间内作为变频器运行状态的评判标准。若检测指标超出置信区间,变频器处于异常运行状态;若检测指标处于置信区间内,则变频器处于正常运行状态。图5为设计的变频器状态监测及分析方法流程图。

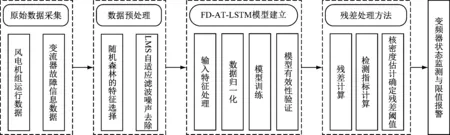
图5 变频器状态监测及分析方法流程图

4 仿真验证及分析

4.1 数据预处理

4.1.1 原始数据采集

以西北某大型风电场某机组为研究对象,采集该机组的风速、风向、叶轮转速和变频器IGBT温度等21个相关变量,采样时间间隔为2 min,同时在SCADA系统中采集到该机组变频器的故障信息。采样时间为2020-04-20—05-10,为期20天,采样点共18 000个。在此期间,变流器故障信息报警3次,如表2所示。

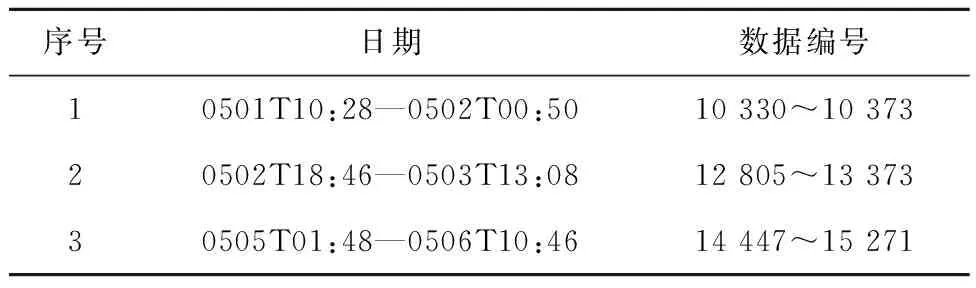
表2 变频器故障信息

4.1.2 基于随机森林的输入特征选择

根据第1节中变频器前后结构进行机理分析得到的结果,选取风速、风向、叶轮转速等20个变量为输入变量,变频器IGBT温度为输出变量,计算基于回归随机森林的特征重要性得分,结果见表3。

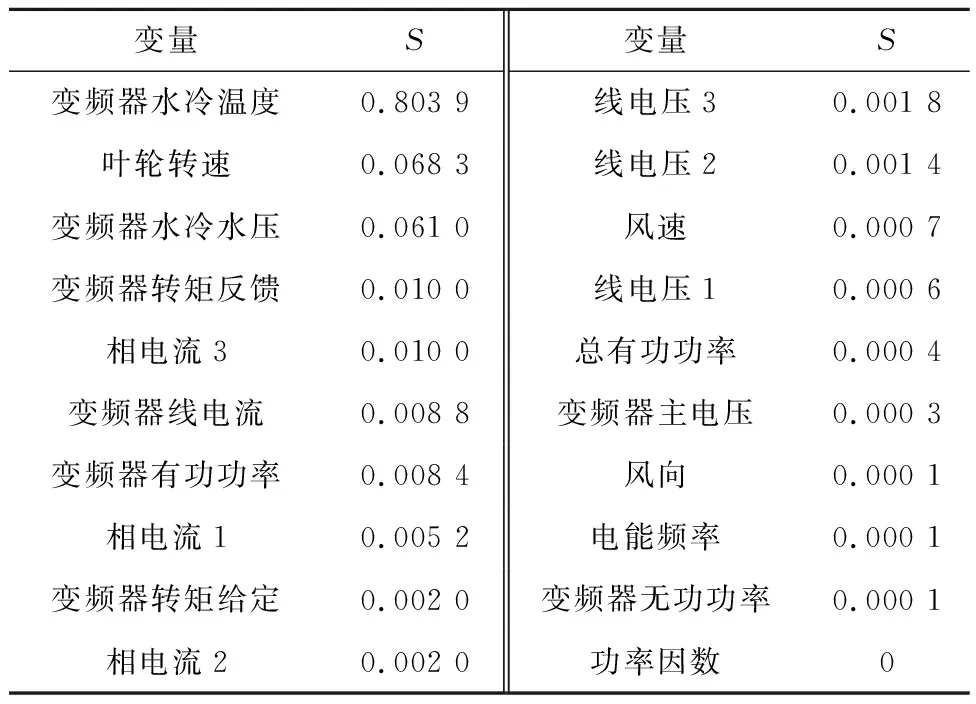
表3 各变量重要性得分

根据计算结果,选取变频器水冷温度、叶轮转速、变频器水冷水压、变频器转矩反馈、相电流1、相电流2、相电流3、线电压2、线电压3、变频器线电流、变频器转矩给定和变频器有功功率12个变量作为模型的输入变量。输出变量的影响因素主要是热能的传递和损失,主要受环境量如变频器水冷温度、水冷水压,气动量如电流电压等,机械量如转矩、发电机转速等影响。因此,基于随机森林的特征选择与基于机理分析的结果相对应,验证了随机森林方法的效果,同时解释了特征选择的物理意义。

4.1.3 基于LMS自适应滤波的噪声滤波

对SCADA系统中所采集到的风速、变频器水冷温度等数据在传输与存储过程中产生的随机噪声进行自适应滤波,如图6和图7所示。结果表明,自适应滤波能够有效地消除数据采集过程中的随机噪声,且对数据进行了平滑处理,处理后的数据毛刺减少,与原数据变化趋势一致,因此可用来直接进行模型训练。

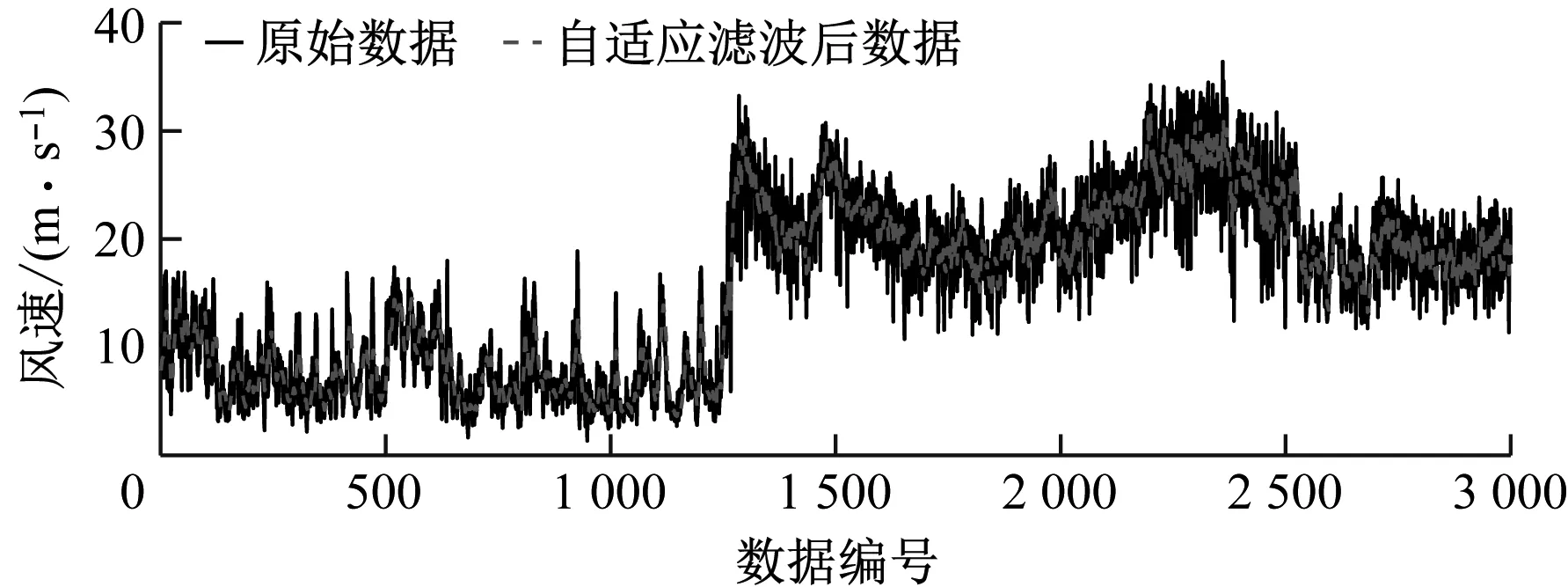
图6 风速数据自适应滤波效果图

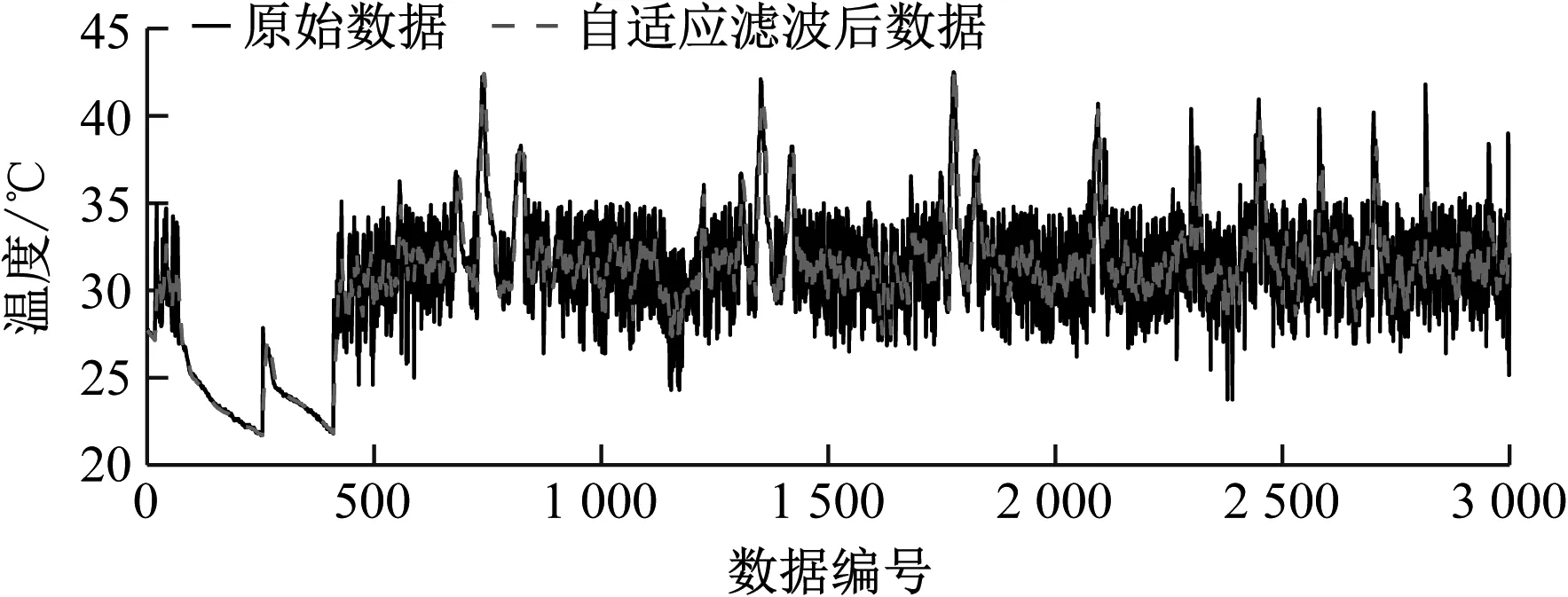
图7 变频器水冷温度数据自适应滤波效果图

4.2 变频器IGBT温度监测模型建立

将采集到的数据以变频器故障信息为基准分为两部分:一部分为前11天未出现故障信息,为正常数据;另一部分为带有故障信息的数据,为异常数据。将正常运行的10 000条数据作为训练集和测试集,按照8∶2的比例分别输入到FD-AT-LSTM模型中进行训练与测试,结果如图8所示。将带有故障样本的异常数据作为验证集用于后续的方法验证。

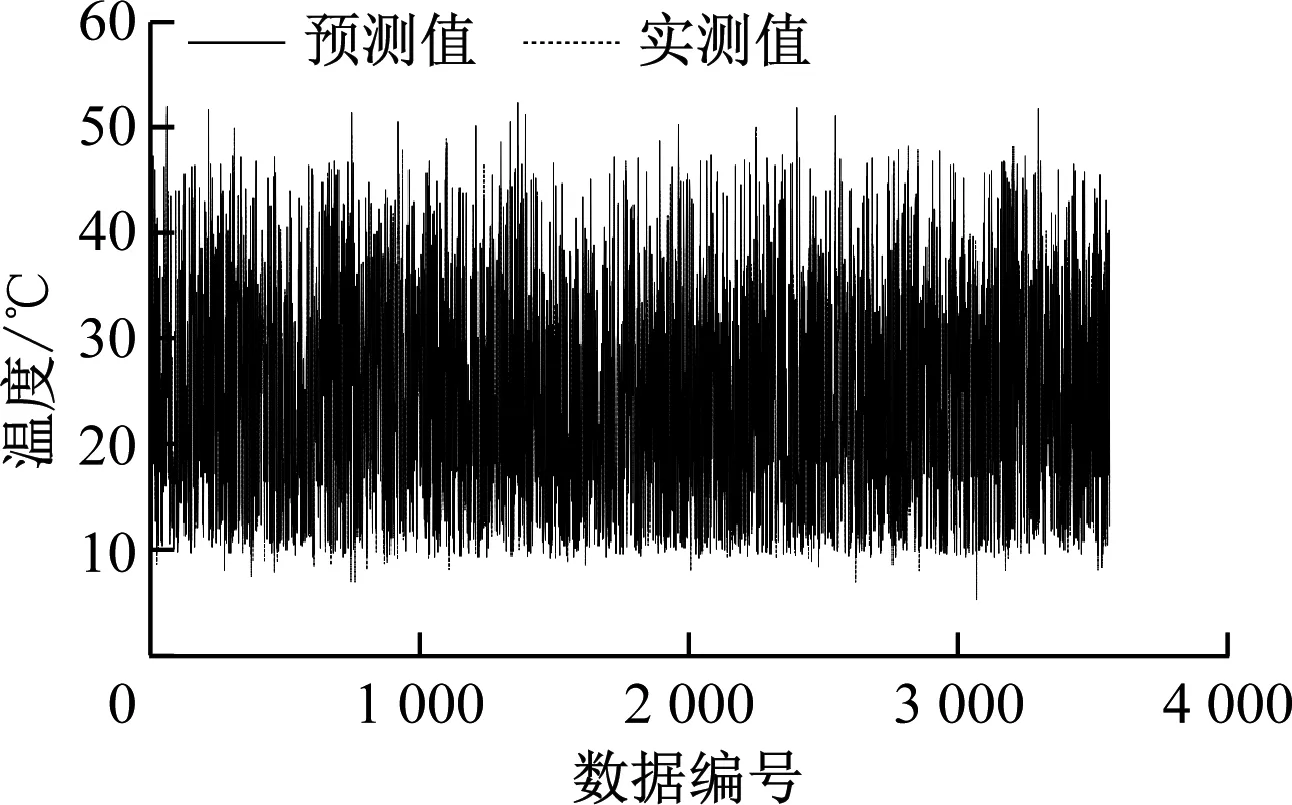
(a) 整个测试集

为了更准确地评价基于注意力机制的长短期记忆神经网络对变频器IGBT温度的监测效果,笔者建立了以下几种基于机器学习方法的变频器IGBT温度监测模型,并对比了各模型的评价指标,具体模型结构说明如下。

回归随机森林模型:决策树个数选取200,最大深度为None。

XGBoost模型:树的最大深度为5,树的个数为500,学习率为0.05,最小叶子节点样本权重和为3。

LightGBM模型:指定叶子的个数为31,树的个数为60,学习率为0.1。

支持向量回归(SVR)模型中,核函数选择'rbf',核函数系数为0.82,正则化系数C选为1。

CNN-LSTM模型:由输入层、卷积层、LSTM层、全连接层和输出层构成,使用Relu作为激活函数。输入层为经数据预处理后的xn个变量,卷积层结构为n×128,LSTM层结构为128×64,全连接层结构为64×10×1。

计算FD-AT-LSTM模型与其他模型的评价指标,结果如表4所示。从表4可以看出,FD-AT-LSTM模型的3个评价指标均优于其他对比模型,因此,FD-AT-LSTM算法的风电机组变频器IGBT温度监测方法是有效的。

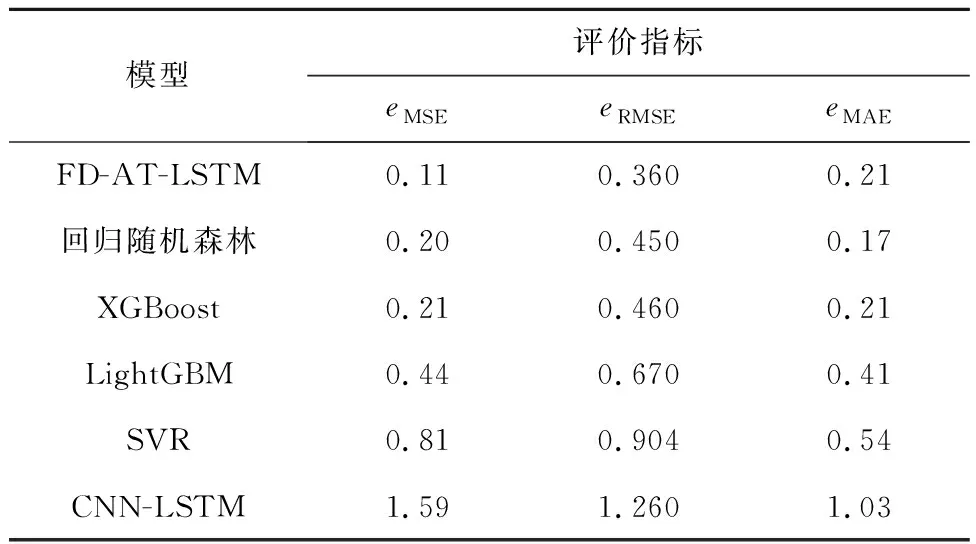
表4 回归模型评价指标

4.3 基于模型残差的监测阈值确定

通过正常样本集建立FD-AT-LSTM模型后,得到了变频器IGBT温度监测模型,若模型的输入变量位于正常工况,则模型预测值与实测值之间具有较小的残差,模型能够较好地拟合输出。当输入变量偏离正常工况时,基于正常样本建立的模型就不能很好地拟合输出,此时残差会增大且明显区别正常数据样本下的残差。

将带有故障样本的异常部分数据作为验证集,输入模型得到残差矩阵后进行检测指标h的计算,通过核密度估计方法计算得到检测指标在98%置信度下的置信区间为[-1.0,0.9],如图9所示,图10为检测指标h的概率密度分布情况。

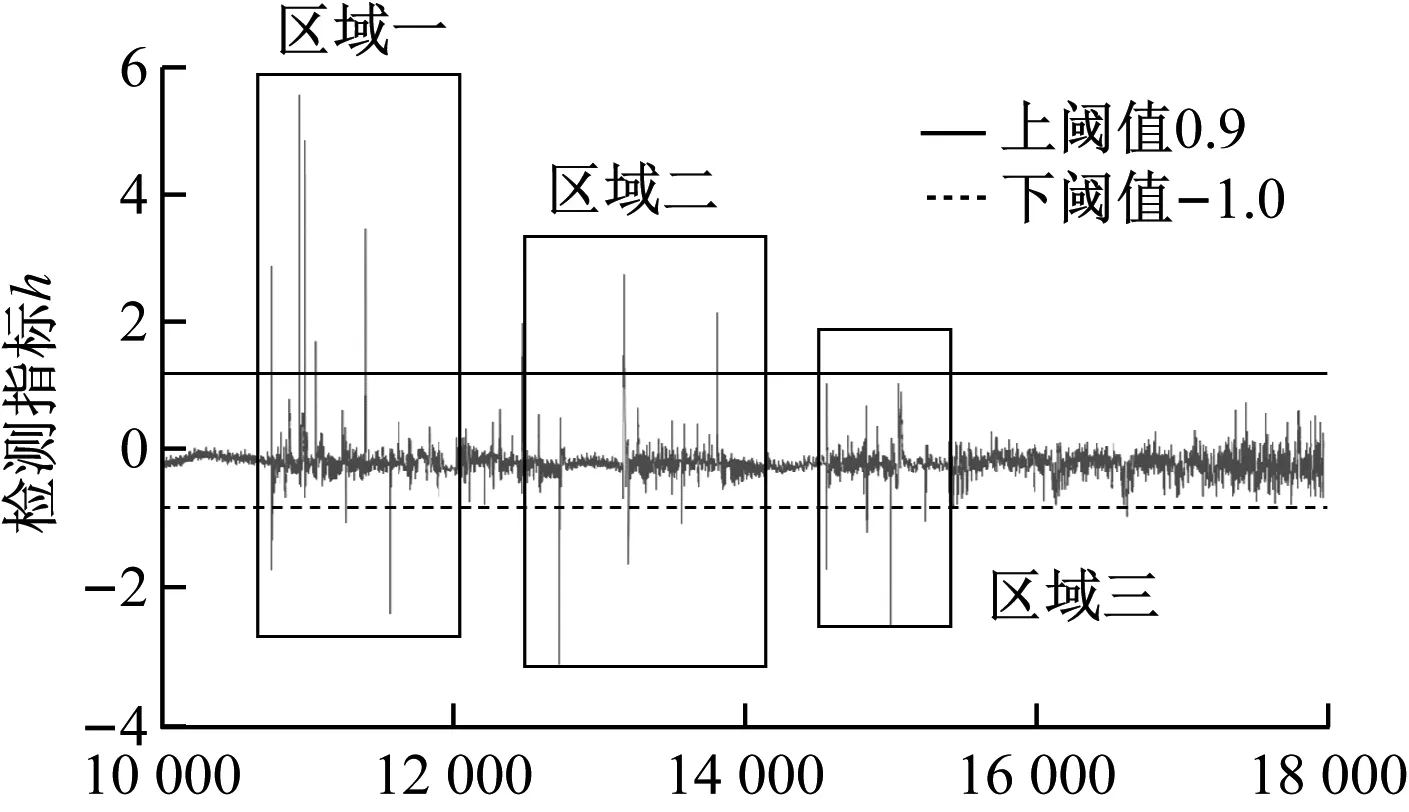
图9 基于检测指标h的预警效果图

从图9可以看出,检测指标h在区域一、区域二、区域三均超出了预先设定的98%置信度的置信区间边界,与表2对应的故障序号1、2、3相对应。且故障1在数据编号10 314处检测指标h超出阈值,提前16步进行预警,故障2在编号12 783处检测指标h超出阈值,提前22步进行预警,故障3在数据编号14 419处检测指标h超出阈值,提前28步进行预警。可以看出,FD-AT-LSTM模型成功识别出了故障信息中的3次故障且均能提前进行判断,因此基于注意力机制长短记忆神经网络的风电机组变频器状态监测方法能够准确地对变频器进行状态监测,并能在故障出现前及时给予预警信息。