基于风电机组转子动能的风电场一次调频功率分配优化
2023-09-26刘克天胡新宇
李 想, 刘克天, 李 军, 胡新宇
(南京工程学院 电力工程学院,南京 211167)
近年来,风电等新能源在我国电源结构中的占比不断攀升。截至2021年底,我国并网风电装机容量32 848×104kW,增长16.6%,占全国总发电装机容量的13.82%[1]。由于国内广泛应用的双馈风电机组和直驱风电机组(下文统一简称风电机组)均通过电力电子装置实现并网,其转子转速与电网频率解耦,因此不具有传统同步机组的惯性响应及一次调频能力[2]。风电大规模并网导致电网的等效转动惯量降低,一次调频能力减弱,对电网的频率稳定性产生新的威胁[3-4]。
随着风电机组大规模并网,风电场需具备类似同步机组的有功控制和频率调节能力[5]。风电场参与系统调频的传统方法要求风电机组在正常运行时降低风能利用率,为调频提供足够的备用容量,然而该方法会严重影响风电场并网的经济性。Hatziargyriou等[6]指出风电场可利用风电机组自身叶片及转子储存的动能参与电网调频,具有较好的经济性和调频潜力。风电机组在调频期间可提供超过一半的转子动能,远超过同步机组的9.75%[7]。刘皓明等[8]指出风电机组利用自身转子动能参与电网调频可有效改善系统暂态频率的最低值,但难以改善系统稳态频率,且风电机组退出调频后会引发频率二次跌落问题。王同森等[9]根据叶片角速度及时调整风电机组调频控制参数,避免了转子动能的过度消耗。Kang等[10]改进了风电机组参与调频期间的功率-角速度变化曲线,减小了风电机组退出调频时刻产生的功率缺额。张正阳等[11]引入了风电机组转速闭环控制环节,避免了风电机组因风速过低而引发的切机脱网现象。
在缓解风电机组退出调频所导致的频率二次跌落问题方面,文献[12]~文献[14]提出了风电机组有序退出法,避免风电机组在短时间内集中退出,能够有效减缓频率二次跌落。随着风电渗透率的增加,单台风电机组直接参与电网调频并不现实,只能以风电场整体形式参与电网调频。在风电场一次调频有功功率分配方面,何廷一等[15]提出了风电机组调频能力的评估标准,避免调频能力不足的风电机组参与调频。基于风电场各风电机组的转子动能储备量,张晨曦等[16]优化了二次调频期间各风电机组的出力大小,减轻了同步机组的调频压力。林俐等[17]对风电机组调频能力进行排序,使调频能力强的风电机组优先参与系统调频。伍双喜等[18]提出了基于风电机组风能利用率的风电场功率分配方法,使风电场在调频期间总体的风能损失最少。Wang等[19]以风电场总体转子动能消耗最少为目标进行功率分配。文献[20]中风电场各风电机组根据自身的转子动能大小采用不同的控制参数参与系统调频。
综上,当前进行风电场功率分配研究时,忽略了风电机组的非线性环节,难以对风电机组的运行工况进行量化分析。因此,笔者对风电场进行单机等值,并开展一次调频功率分配方法研究。首先,以风电机组转子动能为研究对象,对风电场进行单机等值,基于风电场单机等值模型计算风电场整体调频最优控制参数和退出调频时刻转子动能,再根据风电场各风电机组运行工况,建立风电场一次调频风电机组功率分配优化模型,实现风电场调频控制策略从风电场单机等值模型向风电场各风电机组的转换。
1 基于风电机组转子动能的风电场单机等值
假设风电场有nw台初始运行工况不同的风电机组参与系统调频,令第i台风电机组的转子动能为
(1)
式中:Ei为第i台风电机组的转子动能;Ji为第i台风电机组的转动惯量;ωri为第i台风电机组的叶片角速度。
第i台风电机组的惯性时间常数Hwi为
(2)
式中:ωrB为风电机组额定角速度;SB为系统基准功率。
风电场单机等值模型的惯性时间常数Hwall为
(3)
风电场单机等值模型的总转子动能Eall为
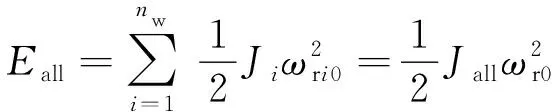
(4)
式中:ωri0为第i台风电机组的初始叶片角速度;ωr0为风电场单机等值模型的等效初始叶片角速度。
(5)
联立式(4)和式(5),可解得ωr0的值。
第i台风电机组的最大功率点跟踪(maximum power point tracking,MPPT)功率Pmppti为
(6)
式中:Kwi为第i台风电机组的MPPT系数。
风电场单机等值模型的总MPPT功率Pmpptall为
(7)
风电场单机等值模型的等效MPPT系数Kwall为
(8)
风电场单机等值模型的总机械功率为
Pmall=Pvall·Cp
(9)
式中:Pvall为风电场单机等值模型的总输入风能;Cp为风电场单机等值模型的风能利用系数。
假设所有风电机组均不采用超速控制,且在调频初始时刻均处于MPPT模式,此时MPPT功率与机械功率相等,因此有
Pmall0=Pmpptall=Pvall·Cpmax
(10)
式中:Pmall0为风电场单机等值模型的初始机械功率;Cpmax为最大风能利用系数。
第i台风电机组叶尖速比λi的表达式为
(11)
式中:Rwi为第i台风电机组的叶片半径;vi为第i台风电机组的初始风速。
风电机组运行在MPPT模式时,始终保持在最佳叶尖速比λopt,因此由式(11)可得风电场单机等值模型的等效风速vavg为
(12)
式中:Rwavg为风电场平均风电机组叶片半径。
风能利用系数Cp受风电机组叶片角速度和桨距角的影响。假设风电机组在调频期间桨距角不变化,此时Cp仅与叶片角速度有关。对Cp进行线性化得
(13)

联立式(9)、式(10)、式(12)和式(13),解得风电场单机等值模型的总机械功率变化量ΔPmall为
ΔPmall=Kcpall·Δωr
(14)
式中:Kcpall为风电场机械功率变化系数,用于表示风电场机械功率变化量与叶片角速度变化量之间的比值;Δωr为风电场单机等值模型的叶片角速度变化量。
(15)
联立式(1)~式(15)可求得风电场单机等值模型的所有参数。
2 风电场一次调频过程分析
2.1 风电场一次调频控制参数优化
将风电场一次调频环节引入系统频率响应(system frequency response,SFR)模型[21],含风电机组一次调频环节的SFR模型如图1所示。图中:H为传统机组惯性时间常数;D为阻尼系数;Km为机械功率增益系数;R为调速器调差系数;FH为汽轮机再热常数;TR为汽轮机再热时间常数;Pd为由负荷变化引起的扰动功率,大于零表示负荷减少,小于零表示负荷增加;Δω为传统机组角速度变化量,标幺值下与系统频率Δf在数值上相等;Kdf为下垂控制系数;Kpf为虚拟惯量系数;ΔPeall为风电场参与调频期间的总电磁功率变化量,小于零表示电磁功率增加,大于零表示电磁功率减少。
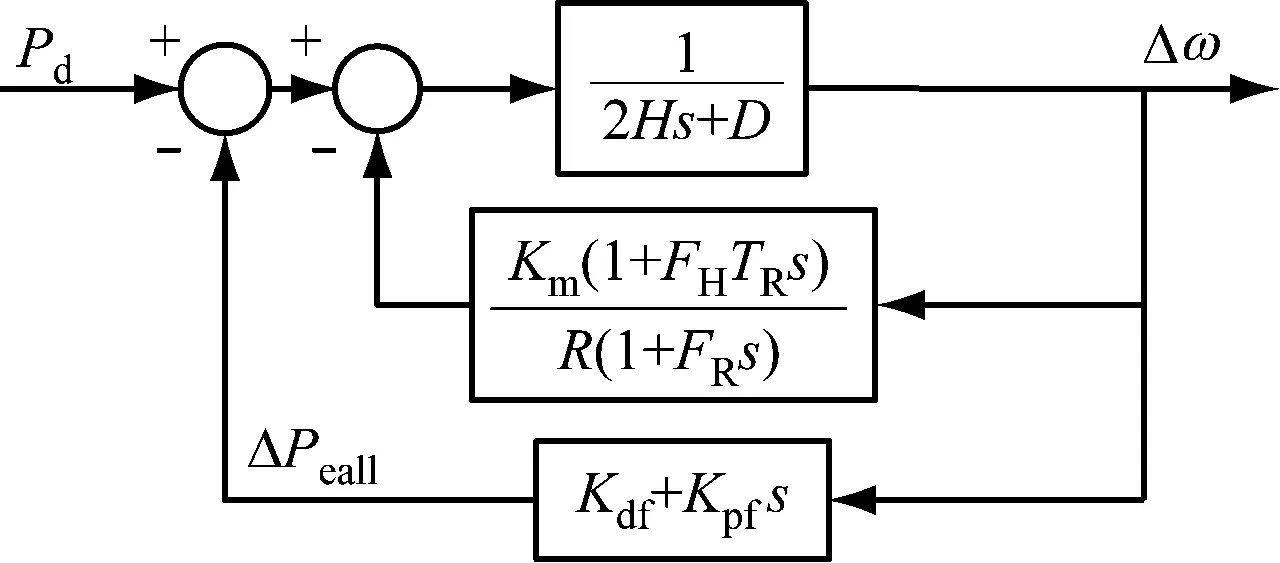
图1 含风电机组一次调频环节的系统频率响应模型
Kdf、Kpf以及风电场退出一次调频的时刻toff是影响系统动态频率的主要因素,将上述3个变量作为解向量并构建优化模型。由于优化时假设风电机组参与一次调频前始终运行在MPPT模式,不存在额外的备用容量,因此相较于可通过切机等方式缓解的频率上扰问题,风电场更难以处理频率下扰问题,故重点考虑频率下扰时的情况。设计优化目标z,使系统一次调频期间的频率最低值最高,其表达式为
z=max(Δfmin)
(16)
式中:Δfmin为系统一次调频最大频率偏移量。
约束条件为
ωroff≥ωrmin
(17)
式中:ωroff为风电场单机等值模型退出调频时刻的叶片角速度;ωrmin为风电场单机等值模型的叶片角速度下限值。
联立式(16)和式(17)可解得使系统动态频率最优的风电场调频控制参数。
2.2 风电场一次调频功率分配模型
图2为风电场单机等值后的角速度变化量模型,用于描述ΔPeall对单机等值模型叶片角速度变化量Δωr的影响。

图2 单机等值模型下的风电场叶片角速度变化量模型
图2中W(s)为风电场单机等值模型的角速度变化量传递函数,其表达式为
(18)
然而,随着风电渗透率的提高,仅用单机等值模型描述风电场参与一次调频的过程并不现实,风电场必须以整体形式参与一次调频。
从风电场的角度出发,考虑风电机组运行工况的差异,将图2转化为风电场内所有参与一次调频的风电机组的集合,把ΔPeall按一定比例分配至各风电机组,如图3所示。

图3 考虑风电机组运行工况差异的风电场角速度变化量模型
图中,Wi(s)为第i台风电机组角速度变化量的传递函数;ki为第i台风电机组的功率分配系数;Δωri为第i台风电机组的角速度变化量。
(19)
式中:Kcpi为第i台风电机组的机械功率变化系数。
(20)
式中:Pvi为第i台风电机组的输入风能。
为保证各风电机组电磁功率变化量之和与ΔPeall严格相等,应使图3中k1~knw之和为1,即
(21)
需要说明的是,尽管图2和图3分别从未进行单机等值和进行单机等值2个角度阐述了ΔPeall对风电机组角速度变化量的影响,在解释力层面是等价的,但当W(s)与Wi(s)不存在比例关系时,图2和图3在公式层面尤其是阶次上不一定存在等价关系。
对图3中Δωri(s)进行反拉氏变换,分别求得各风电机组角速度变化量的时域表达式Δωri(t)。将toff代入Δωri(t),解得各风电机组退出调频时刻的角速度变化量Δωri(toff)。
在理想情况下,所有Δωri(toff)均满足与单机等值模型下退出调频时刻的角速度相等,即
Δωri(toff)=ωroff-ωri0
(22)
由式(22)可反推各风电机组的功率分配系数ki。
由于风电机组本身存在较多的非线性环节,当式(21)与式(22)联立时,可能会出现无解的情况。因此,有必要将式(22)的参数求解问题转变为优化问题。
3 风电场一次调频功率分配系数优化
令ωroff为风电场退出调频时刻的目标叶片角速度。
设计优化目标z1,使风电场各风电机组退出调频时刻的叶片角速度ωri(toff)与目标叶片角速度ωroff的方差最小,表达式为
(23)
解向量ko为风电场各风电机组的功率分配系数:
ko=[k1,k2,…,knw]
(24)
优化除了需满足等式约束条件式(21)外,还应满足以下约束条件。
(1) 该优化主要适用于风电场利用自身转子动能参与调频的方式,因此各风电机组退出调频时刻的剩余转子动能总和与单机等值模型的剩余转子动能的偏差不能过大。为满足工程需求,取相对误差不大于5%,约束条件为
(25)
(2) 各风电机组退出调频时刻的叶片角速度不能低于规定的下限值,约束条件为
ωri(toff)≥ωrimin
(26)
式中:ωrimin为第i台风电机组的叶片角速度下限值。
4 算例分析
取功率基准值为100 MVA,频率基准值为50 Hz,传统机组正常运行时的输出功率标幺值为1,设3台2 MW风电机组参与一次调频,风电机组转子转速基准值为1 500 r/min[22],风电机组齿轮箱转动比为110,风电机组叶片角速度基准值为1.427 3 rad/s,3台风电机组以及单机等值模型的叶片角速度标幺值下限值均为0.7,风电机组平均叶片半径为40 m,最大风能利用系数为0.438 2,最佳叶尖速比为6.325 0,线性化系数为0.046 6,传统机组各参数见文献[21]。
文献[23]中指出,即使在单个风电场内,各风电机组的实时风速仍存在显著差异。因此,本文各算例均假设风电机组存在较大的初始风速偏差,以证明本文优化方法处理初始风速不同的风电机组时仍具有良好的适用性。
另外,风电场退出调频后的转速恢复时间较长,同时风电场电磁功率变化又比较缓慢,对系统暂态频率的影响有限[24]。为便于分析,忽略了风电场转速恢复阶段对系统暂态频率的影响,并假设风电场退出调频后各风电机组角速度均稳定在ωri(toff)。该假设会导致系统频率稳态值低于实际值,但对系统暂态频率最低值几乎没有影响。
使用Matlab中的fmincon函数,对式(21)、式(23)~式(26)构建风电场一次调频功率分配优化模型,验证并分析不同情况下的优化结果。
4.1 算例1:风电场风速偏高时的情况
设系统在初始时刻的扰动功率标幺值为0.1。1~3号风电机组的惯性时间常数标幺值分别为0.1、0.2和0.3,风速分别为10 m/s、12 m/s和14 m/s。风电场单机等值模型下的最优下垂控制系数标幺值为5.128 6,最优虚拟惯量系数标幺值为6.885 6,最优退出调频时刻为6.393 4 s。
优化解得1~3号风电机组的功率分配系数分别为0.035 1、0.441 8和0.523 1。以0.333 3为基准,风电机组功率分配系数的方差为0.045 6。
各风电机组参与一次调频期间的角速度变化量如图4所示,此时风电机组角速度变化量的方差为0.019 8。
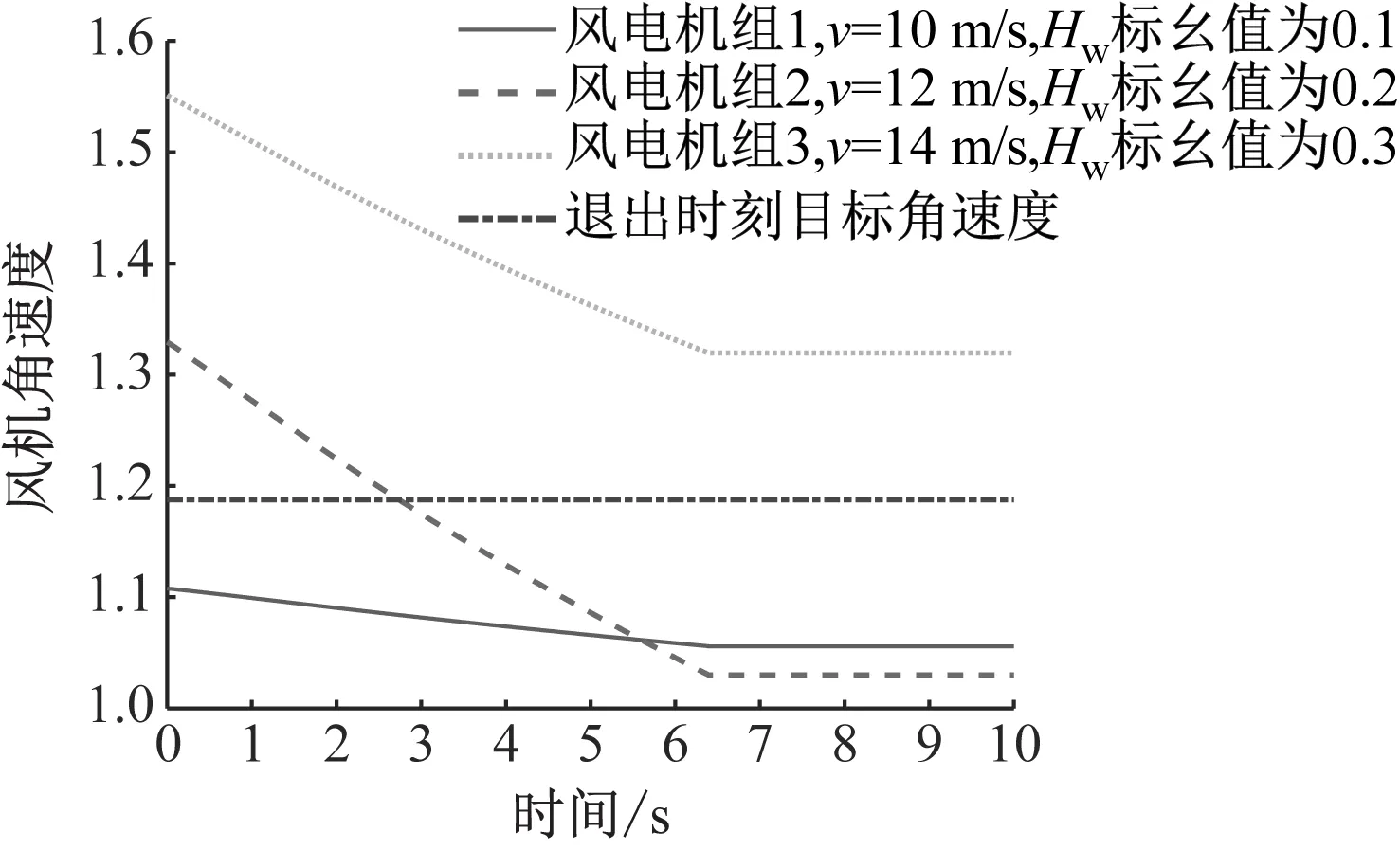
图4 风电场风速偏高时各风电机组的角速度变化量
图5为风电场一次调频功率分配优化前后的系统动态频率曲线对比图。单机等值模型下,系统频率二次跌落最低值为49.671 8 Hz;风电场进行功率分配后的实际频率二次跌落最低值为49.676 6 Hz,相对误差为0.009 7%,满足工程需求。

图5 风电场风速偏高时的系统动态频率对比图
图6为风电场一次调频功率分配优化前后的转子动能对比图。图6中,两者曲线几乎重合,说明在风速相对较大、风电机组转子动能足够充裕的情况下,该优化能达到较好的效果。
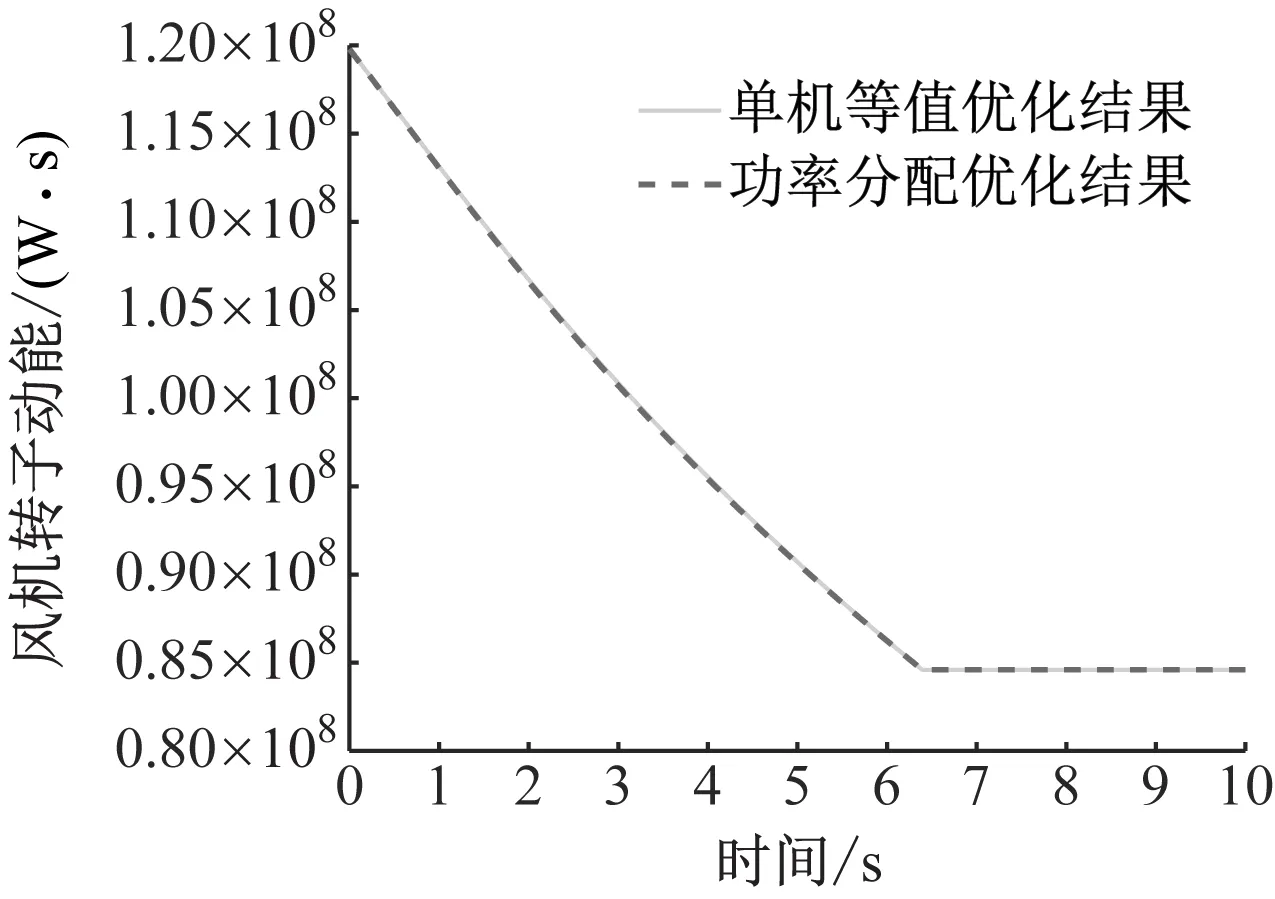
图6 风电场风速偏高时的转子动能对比图
4.2 算例2:风电场风速偏低时的情况
进一步研究风速较低时的情况。设系统在初始时刻的扰动功率标幺值为0.1。1~3号风电机组的惯性时间常数标幺值分别为0.1、0.2和0.3,风速分别为7 m/s、9 m/s和11 m/s。风电场单机等值模型下的最优下垂控制系数标幺值为6.546 0,最优虚拟惯量系数标幺值为10.053 5,最优退出调频时刻为7.135 0 s。
优化解得1~3号风电机组的功率分配系数分别为0.008 2、0.293 9和0.697 9。以0.333 3为基准,风电机组功率分配系数的方差为0.080 1。
3台风电机组的角速度变化量如图7所示,风电机组角速度变化量的方差为0.002 3。
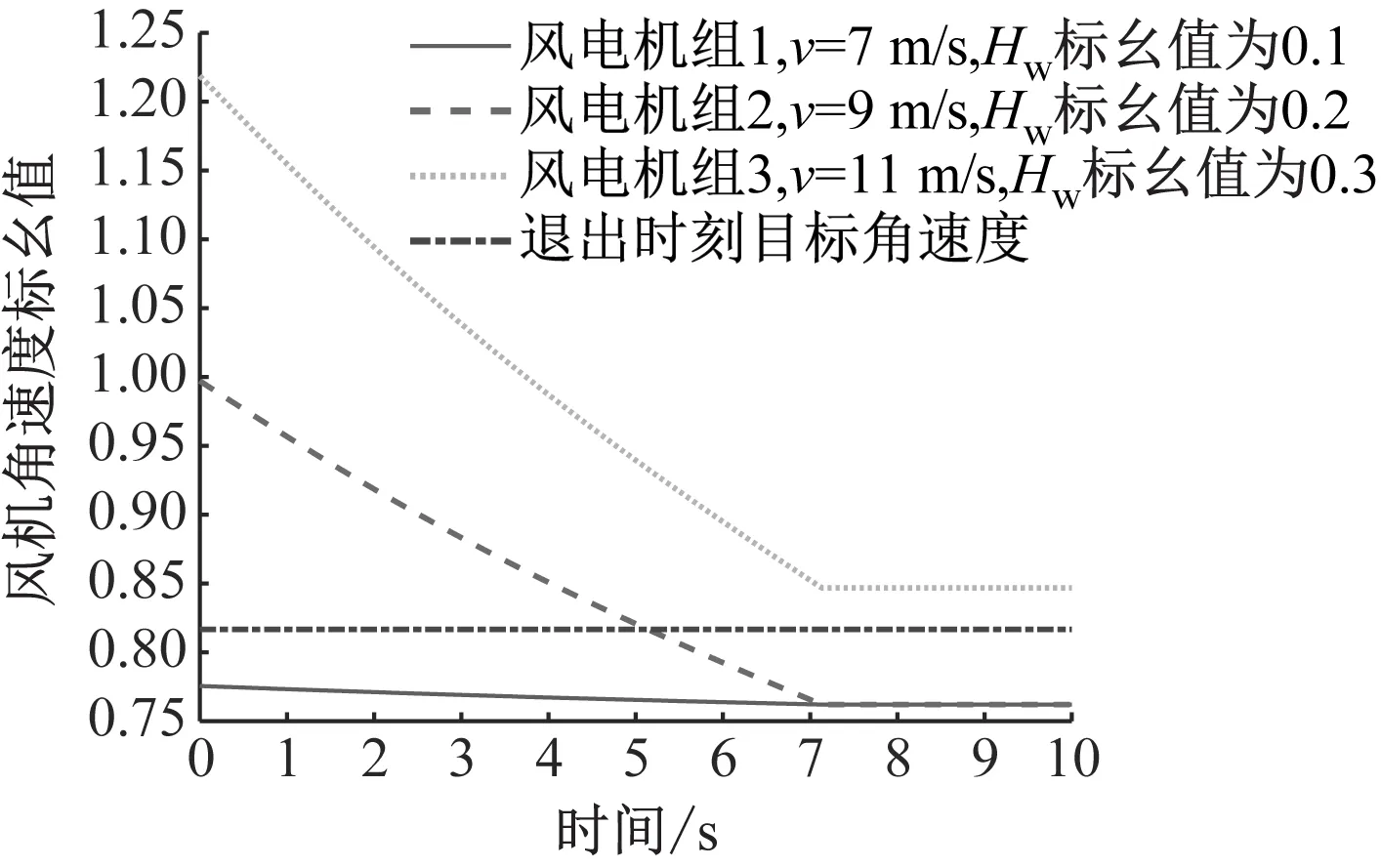
图7 风电场风速偏低时各风电机组的角速度变化量
图8为系统动态频率曲线对比图。单机等值模型下,系统频率二次跌落最低值为49.701 3 Hz;风电场进行功率分配后的实际频率二次跌落最低值为49.704 3 Hz,相对误差为0.006 1%,满足工程需求。

图8 风电场风速偏低时的系统动态频率对比图
图9为风电场转子动能对比图。不同于算例1,此时风电场实际退出时刻的剩余转子动能小于单机等值模型下的结果,相对误差为-2.71%,仍在约束条件式(25)的允许范围内。
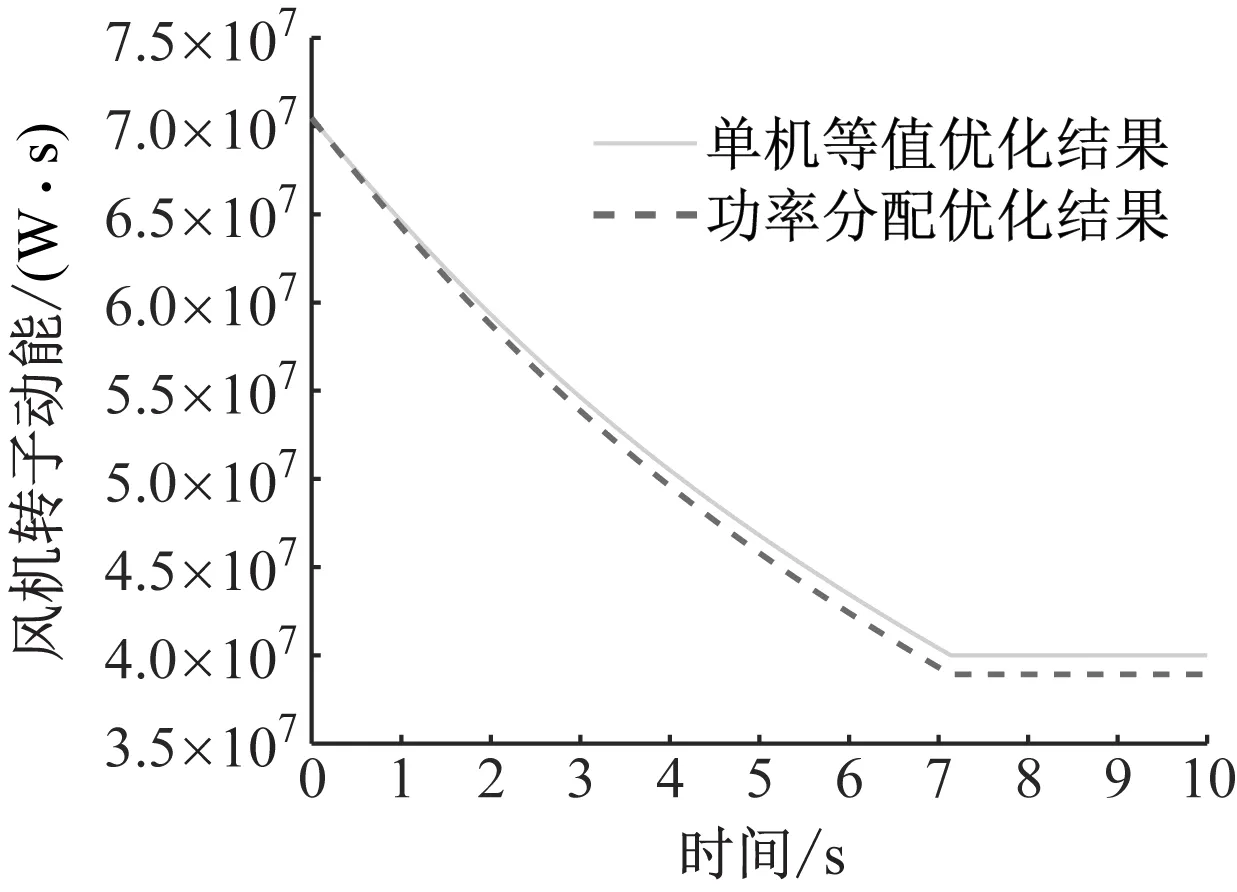
图9 风电场风速偏低时的转子动能对比图
为找出图9中偏差产生的原因,需暂时去除约束条件式(26),并再次对算例2的数据进行优化。此时风电场单机等值模型的最优控制参数保持不变,风电机组1的功率分配系数变为0.092 8,风电机组2的功率分配系数变为0.397 5,风电机组3的功率分配系数变为0.509 7。
此时,3台风电机组的角速度变化量如图10所示。转子动能变化量如图11所示。图11与算例1的情况类似,2条曲线几乎重合,不存在明显偏差。
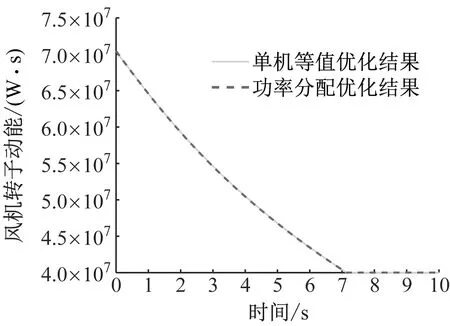
图11 风电场风速偏低且不计及风电机组角速度限制时的风电场转子动能对比图
对比前后2次的功率分配系数以及图7、图9~图11可知,约束条件式(26)限制了初始转速较低的风电机组的功率分配系数取值范围,并使初始转速较高的风电机组承担更大的系数。这导致图10中风电机组3的角速度变化量明显大于图7中。
表1给出了不同约束条件下,各风电机组在退出一次调频时刻剩余转子动能的差异。由表1可知,风电机组1和2因约束条件式(26)少消耗的转子动能小于风电机组3因约束条件式(26)多消耗的转子动能,因此图9中2条曲线会存在偏差。这也间接表明,高转速风电机组承担较大的功率分配系数,会过度消耗风电场整体的转子动能。
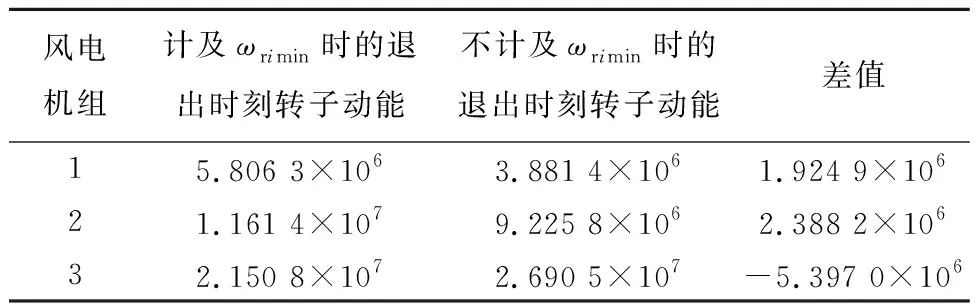
表1 不同约束条件下风电机组退出一次调频时刻剩余转子动能的对比
4.3 算例3:风电场风速偏低且扰动功率较大的极端情况
最后研究优化模型在低风速、大扰动等极端环境下的情况。设系统在初始时刻的扰动功率标幺值为0.2。1~3号风电机组的惯性时间常数标幺值分别为0.1、0.2和0.3,风速标幺值分别为7 m/s、9 m/s和11 m/s。风电场单机等值模型下的最优下垂控制系数标幺值为6.582 6,最优虚拟惯量系数标幺值为2.316 3,最优退出调频时刻为4.650 5 s。
当设定单机等值模型风电机组叶片角速度标幺值下限值为0.7时,优化不收敛。原因如下:首先,由算例2可知,当风速较低且风电机组转子动能不足时,风电场整体消耗的转子动能多于单机等值模型下的情况。其次,当系统发生大扰动时,风电场单机等值模型下消耗的转子动能已经非常接近极限值。综合这两点可知,优化可能存在风电场实际消耗的转子动能超过自身可用转子动能总量的情况,这正是造成优化不收敛的主要原因。
为解决该问题,需调整ωrmin的大小,为风电场实际转子动能的偏差留有裕量。令风电场单机等值模型的转速标幺值下限值为0.75,再次进行优化,此时优化收敛。优化解得风电机组1的功率分配系数为0.012 6,风电机组2的功率分配系数为0.256 5,风电机组3的功率分配系数为0.730 9。以0.333 3为基准,风电机组功率分配系数的方差为0.088 9。
3台风电机组的角速度变化量如图12所示,风电机组角速度变化量的方差为1.29×10-4。

图12 风电场风速偏低且系统扰动功率较大时各风电机组的角速度变化量
图13为系统动态频率曲线对比图。在单机等值模型下,系统频率二次跌落最低值为49.365 0 Hz;风电场进行功率分配后的实际频率二次跌落最低值为49.372 2 Hz,相对误差为0.014 5%,满足工程需求。

图13 风电场风速偏低且系统扰动功率较大时的系统动态频率对比图
图14为风电场转子动能对比图。风电场退出一次调频时刻剩余转子动能的相对误差为-3.20%,在误差允许范围内。

图14 风电场风速偏低且系统扰动功率较大时的风电场转子动能对比图
综上,当出现系统扰动过大且风电场转子动能储备不足的情况时,应视情况调整ωrmin的大小。改进后的优化流程如图15所示。
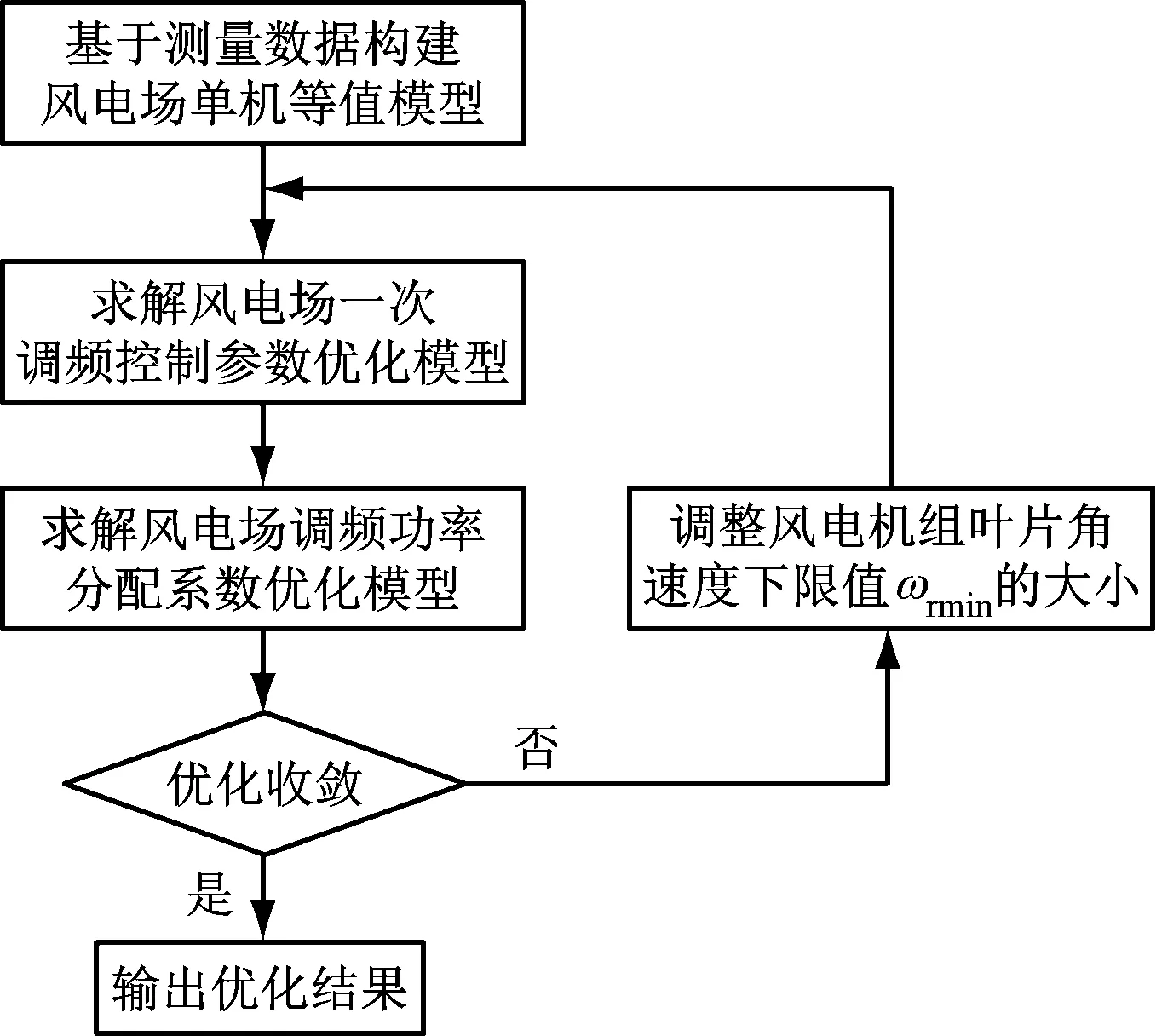
图15 改进后的风电场调频功率分配优化流程图
5 结 论
(1) 基于风电机组转子动能构建的风电场单机等值模型能较为准确地描述风电场参与一次调频期间的转子动能变化过程。
(2) 本文优化方法能根据风电机组的实际运行工况设置合理的调频功率分配系数,有效避免风电机组转子动能的过度释放。
(3) 本文方法的误差均在允许范围内,可用于指导实际的工程应用。
