超临界二氧化碳组合型干气密封性能分析

王 智, 吴雨筱, 韩 旭, 蔡文奎, 孟金祥

(华北电力大学 河北省低碳高效发电技术重点实验室, 河北保定 071003)

随着能源领域的发展和装备制造技术的不断进步,发电机组正朝着大型化和高效化方向发展[1]。为实现“碳达峰”、“碳中和”的目标,需对能源结构进行调整,降低化石能源的消耗量,并加强对低品位热源的利用。超临界二氧化碳(SCO2)作为一种新型的做功工质,其临界温度为31 ℃,临界压力为7.38 MPa,具有密度高、比热容大、黏度低、压缩系数小、无毒无害和化学性能稳定等优点[2-3]。此外,SCO2密度接近液体密度,黏度接近气体黏度,同时具备液体的传热载热能力和气体的流动性能,被认为是最理想的热能循环工质之一[4-6]。

密封部件作为SCO2循环中压缩机和透平的关键配件,对整个循环系统的效率起着非常重要的作用。相较于传统的迷宫密封和刷式密封,干气密封具有泄漏量小、磨损功耗小、使用寿命长和系统稳定性高等优点[7],尽管其结构复杂,但已经成为SCO2旋转做功部件轴端密封的首选[8]。Fairuz等[9]研究了在近临界点和远离临界点2种条件下干气密封的稳态性能,发现在临界点附近使用理想气体方程时误差较大,而真实气体状态方程能准确模拟密封性能。Du等[10]基于真实气体模型,采用热流固耦合方法研究不同槽深下SCO2干气密封性能,分析了进口温度、进口压力、速度和膜厚对密封性能的影响。许恒杰等[11]借鉴考虑惯性效应的气体止推轴承理论,考虑了阻塞流效应和气膜黏度变化,分析层流状态下干气密封的稳态性能。沈伟等[12]在考虑惯性项和实际流态的膜压基础上,采用有限差分法得到膜压,对比分析了实际修正模型和经典简化模型的高速SCO2干气密封气膜刚度和泄漏率。刘柯炜等[13]建立了SCO2变黏度、变密度条件下的雷诺方程,求解得到开启力、泄漏量、摩擦扭矩和气膜刚度等参数。杨青等[14]建立了在惯性效应下黏度和密度发生改变时螺旋槽干气密封动态特性的数学模型,采用有限差分法和小扰动法求解SCO2干气密封的动态特性参数,分析了远离及靠近临界点2种工况下,SCO2干气密封动态特性的变化规律以及惯性效应对其的影响。

笔者在经典螺旋槽干气密封[15]的基础上进行改型,基于叠加组合原理,建立一种组合型螺旋槽密封端面,将其应用于SCO2压气机轴端密封,并构建SCO2实际气体模型,分析在临界点附近其端面几何参数对干气密封气膜开启力、泄漏量和刚漏比的影响。

1 数值模型

1.1 流体域的基本假设

螺旋槽干气密封中的流场计算十分复杂,为了简化计算,作出如下假设[16]:(1) 密封端面刚性良好且光滑;(2) 润滑气体为牛顿流体,气体在流动过程中与固体壁面无滑移;(3) 忽略系统振动对流场的影响;(4) 固体的材料特性保持不变,不考虑形变的影响;(5) 忽略粗糙度对密封的影响;(6) 动静环温度保持不变,忽略摩擦产生的热量对流场的影响。

1.2 流动控制方程

1.2.1 流动因子

定义流动因子a来判断干气密封中的流动状态,流动因子考虑了径向流动和周向流动产生的影响,用流动因子的大小来判断流体的流动状态,a>1时表示紊流,a<1时表示层流[17]。

(1)

(2)

(3)

式中:r为旋转半径,mm;ρ为密度,kg/m3;Rec为径向雷诺数;Rep为切向雷诺数;ω为旋转轴的转速,r/min;h为气膜厚度,μm;μ为动力黏度,Pa·s;Vr为流体的相对速度,m/s。

1.2.2 连续性方程

采用求解雷诺平均Navier-Stokes (RANS)方程来模拟流体,将其应用于旋转系统。对于单旋转坐标系,连续性方程为:

∇·(ρvr)=0

(4)

式中:vr为相对速度向量。

1.2.3 动量守恒方程

动量守恒方程如下:

∇(ρvrvr)+ρ(2ω0×vr+ω0×ω0×r)=-∇p+

∇·τ

(5)

式中:ω0为角速度向量;p为压力,Pa;τ为应力张量。

1.2.4 能量守恒方程

能量守恒方程如下:

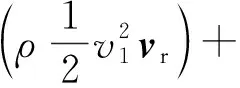
∇(τ·vr)

(6)

vr=v-ur

(7)

ur=ω0×r

(8)

式中:H为焓,kJ/kg;v为绝对速度向量;v1为相对速度,m/s;u1为旋转速度,m/s;ur为旋转速度向量;T为温度,K;k为热导率,W/(m·K)。

1.3 状态方程

由于CO2在临界点附近表现为高度非线性,理想气体状态方程已无法满足计算准确度的要求,因此必须采用实际气体状态方程[18]。在接近CO2临界点时Span Wagner多参量状态方程具有优异的性能,在模拟计算时准确度较高,因此采用Span Wagner方程[19]。Span Wagner状态方程表示为:

(9)

式中:A为亥姆霍兹自由能;R为气体常数;φ为量纲-亥姆霍兹自由能;φ0为量纲-亥姆霍兹自由能理想部分;φr为量纲-亥姆霍兹自由能减少量;δ为密度比例系数;τ1为温度比例系数。

1.4 稳态性能参数

判断干气密封稳态性能的主要参数包括气膜开启力F、泄漏量Q[16]、气膜刚度K及刚漏比Г。其中,气膜开启力是指维持干气密封正常运转,使动静环形成稳定气膜所需的轴向推力;泄漏量是指单位时间从密封系统内泄漏的气膜中的流体总量;气膜刚度为气膜开启力与气膜厚度的比值,其大小可反映密封系统的抗扰动能力;刚漏比是气膜刚度与泄漏量的比值,可用于评价密封在相同泄漏量下形成的气膜刚度,是反映密封综合性能最重要的指标。

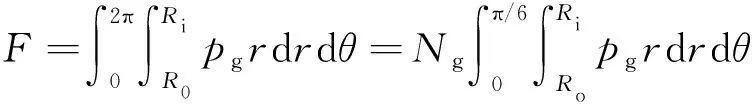
(10)

(11)

(12)

(13)

式中:pg为气膜作用于静环端面某处的压力,Pa;Ri和Ro分别为密封内半径和外半径,mm;h为气膜厚度,μm;θ为柱坐标系下的极角;Ng为槽数。

2 物理模型建立及网格划分

2.1 组合型螺旋槽物理模型的建立

以组合型螺旋槽模型为研究对象,在传统螺旋槽的基础上,再增加一个窄螺旋槽结构,动环开槽端面结构如图1所示。该组合型螺旋槽由外径周向的宽螺旋槽和沿宽螺旋槽根部的窄螺旋槽组合而成。其设计原理是在密封运行时,动环旋转产生泵吸效应,带动密封气体周向流入宽螺旋槽并径向运动,由于入口面积减小,气体流入窄螺旋槽时被压缩,提高了端面的气膜开启力,同时槽区面积减小也降低了工质泄漏量。由于模型具有周期对称性,为了节省计算资源并提高计算效率,选择模型的1/Ng作为计算域。为便于观察,在流体域轴向放大1 000倍。图1为整体气膜模型以及1/Ng的气膜模型。组合型螺旋槽结构的几何参数如表1所示。

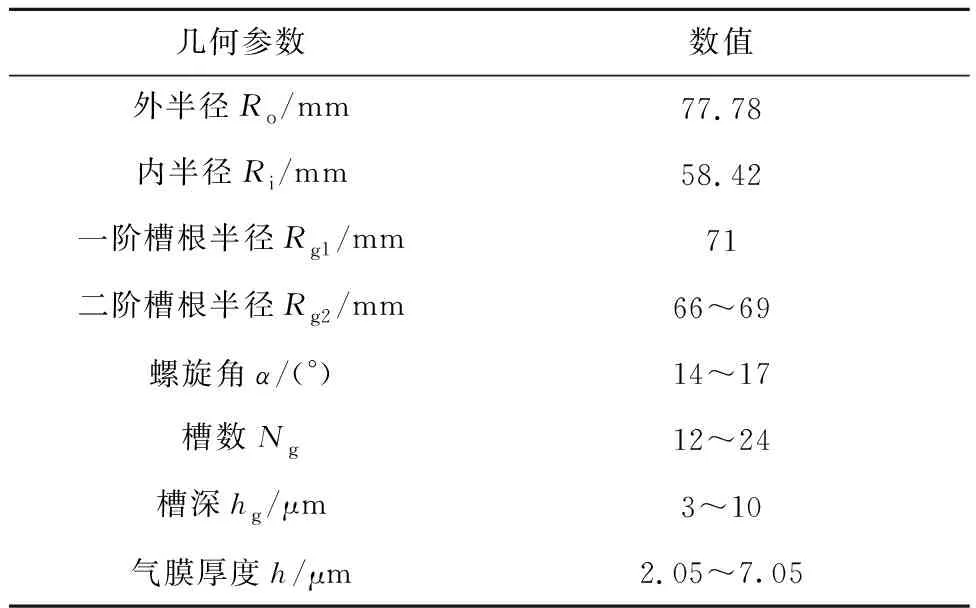
表1 组合型螺旋槽结构几何参数

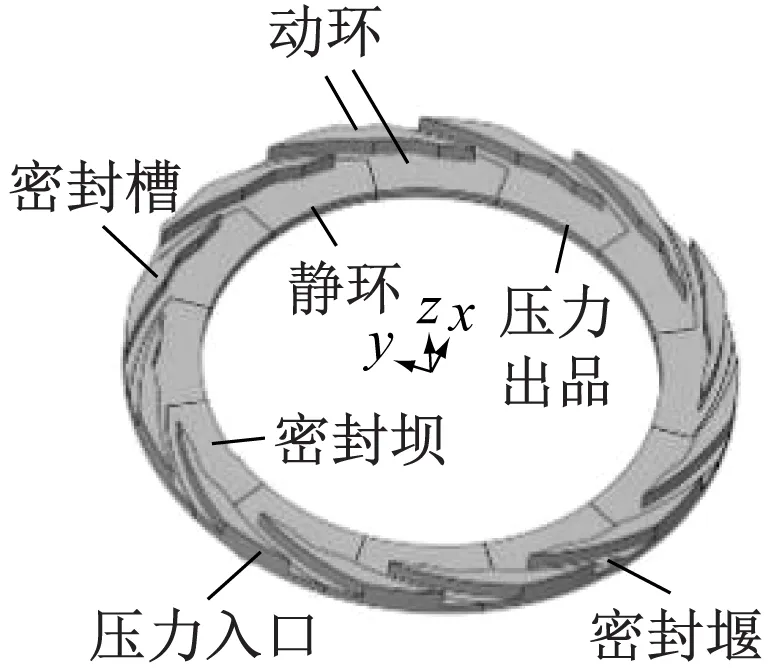
(a) 圆周气膜模型

2.2 计算域网格划分及网格无关性验证

将建好的模型保存为step格式,先将其导入DesignModeler,对每个面进行定义,再导入ICEM中进行网格划分。由于端面气膜厚度和开槽深度为微米级别,与干气密封半径尺寸差距过大,为便于网格划分,将轴向尺寸扩大1 000倍,使其与半径处于相同的尺寸级别,网格模型见图2。流场具有中心对称性,取1/Ng为计算域进行网格划分,采用周期性边界条件进行设置,即p(θ+2π/Ng)=p(θ)。将与动环接触的流体表面部分设为无滑移壁面,与静环接触的流体表面设为反旋转壁面。流体域的入口边界条件设置为压力入口,出口边界条件设置为压力出口,稳态可压缩RANS方程采用隐式分离三维有限体积法求解。动量方程和能量方程均采用二阶精确迎风离散格式,压力采用Standard格式。采用SST湍流模型,密封介质为SCO2。采用SIMPLEC算法实现压力-速度耦合,以减小由于非正交网格而产生的误差。干气密封工况参数如表2所示。

表2 干气密封工况参数

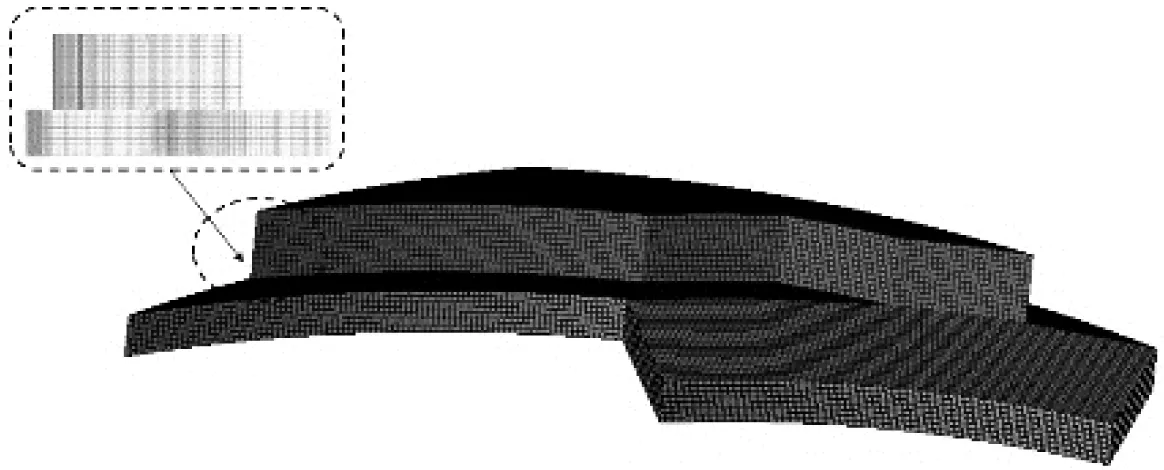
图2 1/Ng模型的网格结构示意图

网格数量设置对Fluent数值模拟的计算精度和计算速度有明显影响。以气膜厚度为3.05 μm、槽深为5 μm、槽数为12、螺旋角为15°、入口压力为10 MPa和出口压力为0.1 MPa为例,分别选择网格数量为62 835、100 772、180 531、262 470和332 015。表3为网格无关性参数对比结果。当网格数量达到180 531时,泄漏量相对误差小于1%,满足网格无关性要求。

表3 网格无关性参数对比

2.3 CO2物性参数处理

CO2在临界点附近表现出强烈的非线性特点,CO2的密度和黏度变化如图3所示。目前,普遍采用由NIST开发的物性数据库查询软件REFPROP来获取SCO2的物性参数[16]。通过Spyder软件调用CO2物性参数,并通过Fluent中的UDF接口导入编写好的物性数据,构建SCO2物性数据库,对其密度、比热容、黏度和热导率进行编程编译,从而保证在临界点附近CO2物性参数的准确性。

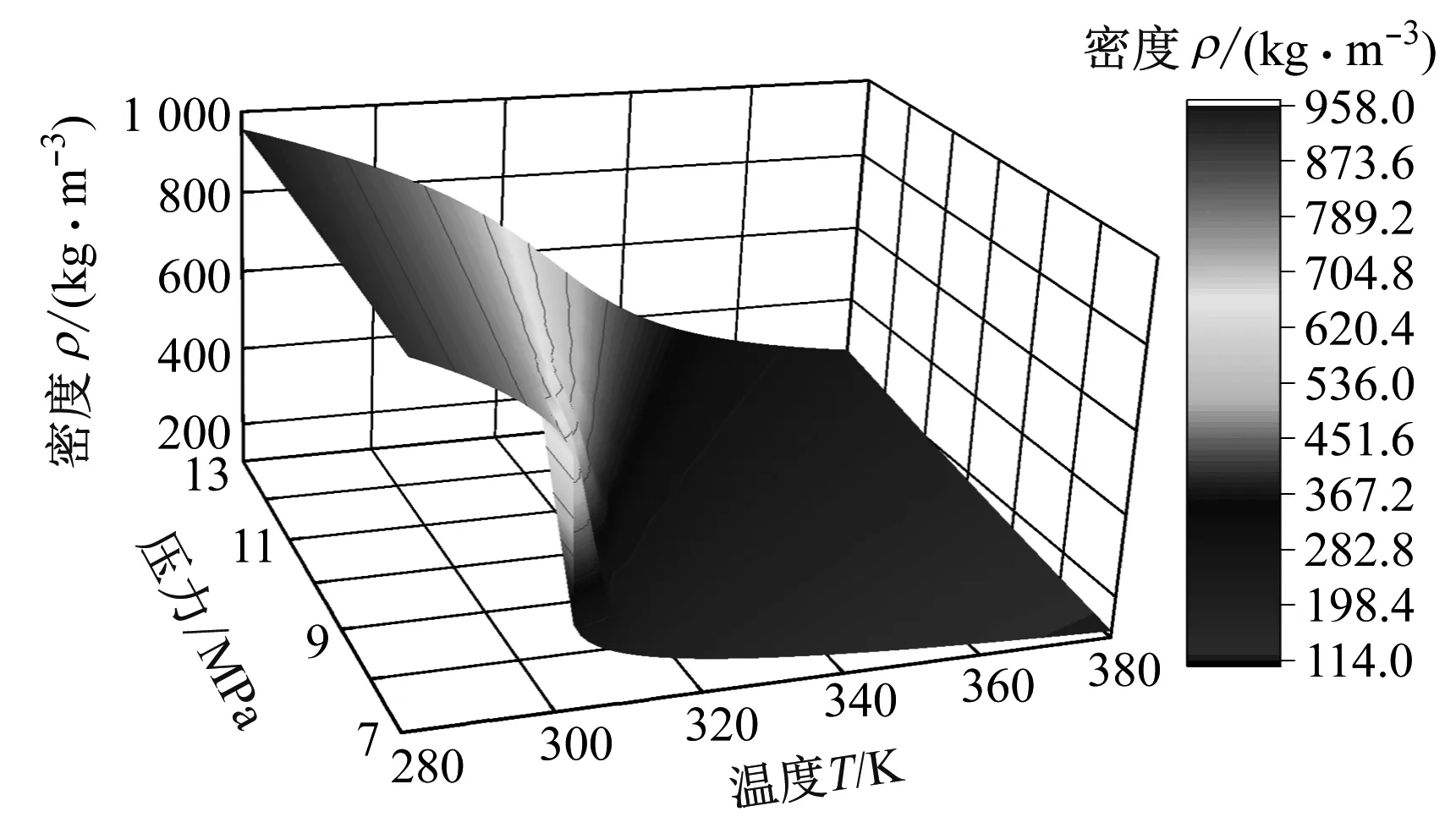
(a) CO2密度

3 结果及分析

在考虑实际气体效应、惯性效应和湍流效应的基础上,对经典螺旋槽干气密封和组合型螺旋槽干气密封的性能进行对比,重点研究临界点附近槽长、槽深、螺旋角和气膜厚度等几何结构参数对SCO2组合螺旋槽密封性能的影响。由于动环旋转使得流体产生切向剪切运动,密封内的流体受到离心作用,会影响密封性能。使用SCO2作为密封介质,相较一般工作介质,SCO2具有较高的密度,临界点附近密度变化比较剧烈,离心效应更强烈,进而影响流体的流动。因此,需对离心效应、惯性效应和黏性泵送等影响密封性能的重要因素进行分析。

3.1 螺旋槽干气密封与组合型螺旋槽干气密封性能的比较

以槽长为69 mm、螺旋角为15°、槽数为12、槽深为5 μm、膜厚为3.05 μm、入口压力为10 MPa、出口压力为0.1 MPa、入口温度为360 K以及转速为10 000 r/min为例,对比螺旋槽干气密封与组合型螺旋槽干气密封的性能。图4为螺旋槽干气密封和组合型螺旋槽干气密封气膜开启力和泄漏量的柱状图。窄螺旋槽的存在增强了组合型螺旋槽干气密封气膜端面的动压效应,使得密封端面气膜开启力提高1.1%,密封的支撑力更大,有利于形成稳定的气膜。与螺旋槽干气密封相比,组合型螺旋槽的泄漏量降低了18.8%,密封作用更好。因此,相较于螺旋槽干气密封,组合型螺旋槽干气密封的综合性能明显提升。

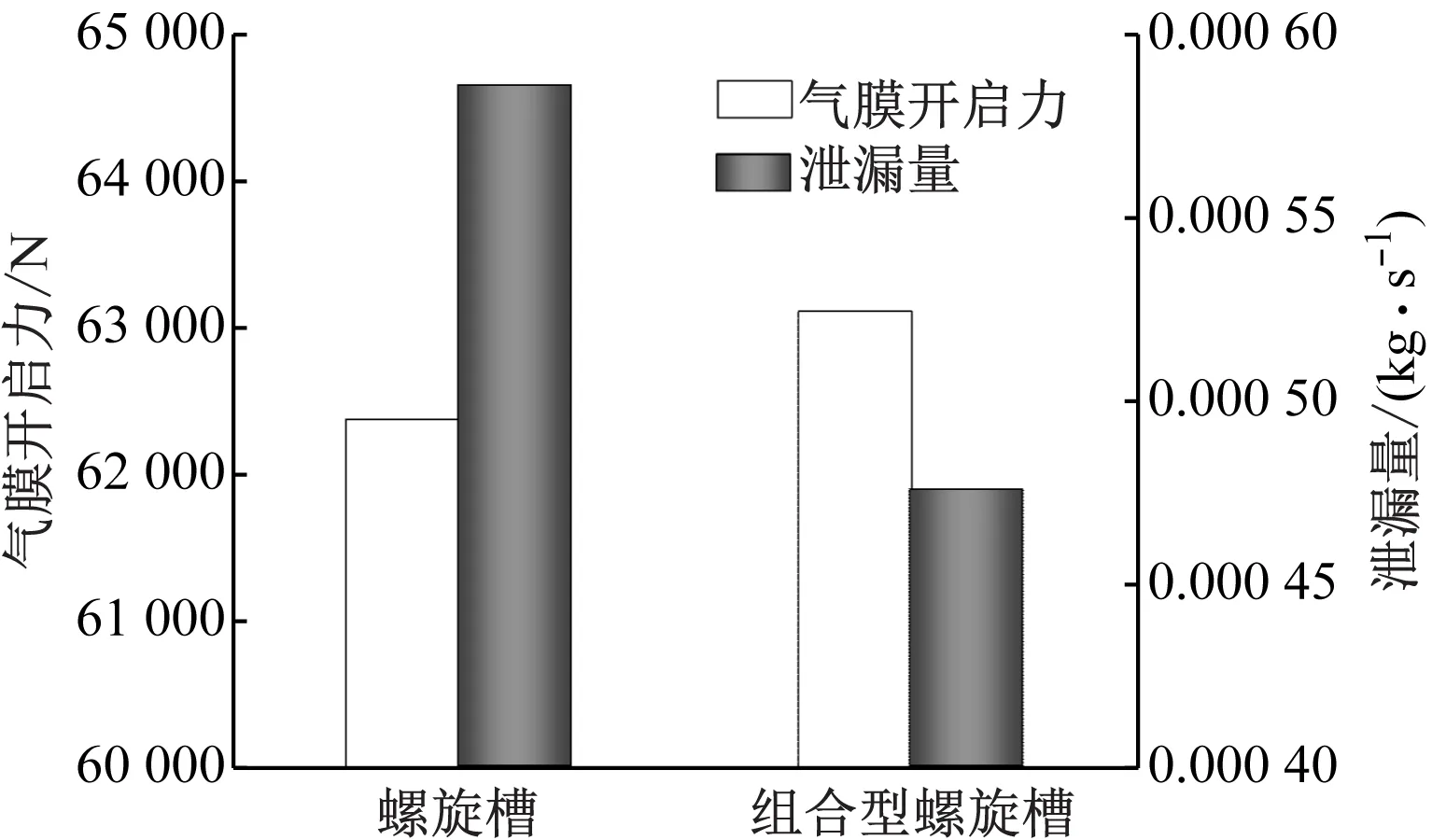
图4 螺旋槽干气密封和组合型螺旋槽干气密封的气膜

3.2 几何参数对组合型螺旋槽干气密封性能的影响

以螺旋角为15°、槽数为12、槽深为5 μm、膜厚为3.05 μm为例。图5(a)为不同槽长下气膜压力分布云图。随着槽长的增加,密封端面最大气膜压力由11 654 834 Pa增加至12 023 131 Pa,窄螺旋槽槽根处的平均膜压也增大。随着槽长的增加,螺旋槽末端形成的局部高压区域扩大。这是由于SCO2密度较高,能够产生强烈的黏性剪切作用和离心效应,从而使得吸入气体增多,在凹槽处形成高压区域,同时黏性剪切作用和离心效应随着槽长的增加而更加明显,具体表现为槽区高压范围变大,密封端面压力峰值增大,这有利于形成更稳定的气膜支撑力。

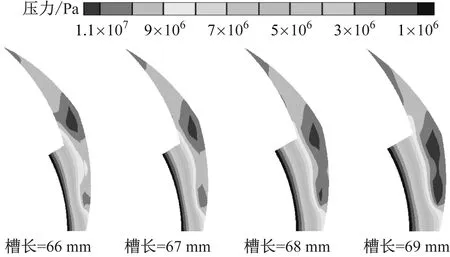
(a) 气膜压力分布云图

图5(b)为不同槽长下气膜开启力、泄漏量和刚漏比的折线柱状图。随着槽长的增加,气膜开启力和泄漏量均下降,刚漏比增大。尽管槽长的增加会使得密封端面压力峰值增大,但实际产生的升力较小,这是由于槽长较大的密封在坝区产生的压力较低,在离心效应的作用下,靠近坝区外径区域的压力下降更快,同时坝区面积增加,导致气膜开启力下降。泄漏量下降的原因是随着槽长的增加,密封端面坝区变宽,产生的黏性摩擦效应和离心效应较强,这有利于阻碍流体向外流出,降低泄漏量。槽长由66 mm增加至69 mm时,端面气膜开启力下降0.35%,泄漏量下降12.73%,刚漏比增加13.34%。由此可知,槽长对泄漏量的影响较大,密封性能随槽长的增加而提高。

以螺旋角为15°、槽数为12、槽长为69 mm、膜厚为3.05 μm为例。图6(a)为不同开槽深度下的气膜压力云图。随着开槽深度的增加,密封端面最大膜压逐渐增大,在开槽深度为10 μm时槽根达到最大膜压(15 601 827 Pa)。其原因是在槽深增加的影响下组合型螺旋槽产生了更强烈的阶梯效应,由于窄螺旋槽处流通通道突然变小,气体之间的相互作用更强烈,有效受力面积增大,更有利于CO2分子间碰撞,从而在螺旋槽根处达到最大膜压。但是,膜压与槽深的关系并非简单的正相关关系,在槽深达到一定厚度时,阶梯效应不会无限提高,反而会因密封坝区域泵送效应不足而导致端面最大膜压下降。

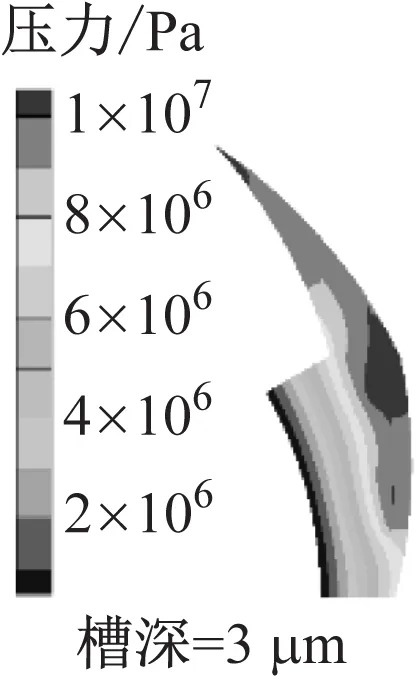
(a) 气膜压力云图

图6(b)为不同开槽深度下气膜开启力、泄漏量和刚漏比的折线柱状图。随着槽深的增加,气膜开启力和泄漏量增大,刚漏比降低。槽深由3 μm增加至10 μm时,气膜开启力和泄漏量分别增大27.58%和43.24%,刚漏比下降10.93%。由于密封端面压力峰值随着槽深的增加而增大,在凹槽末端压力达到最大,此处密封动压效应增强,整个密封端面的压力提高,有利于形成稳定的气膜开启力。槽深的增加也使得槽区面积增大,动环旋转流体产生切向运动的能力降低,密封坝区离心效应减弱,使得泄漏量明显增大,密封综合性能随槽深的增加而降低。

以槽深为5 μm、槽数为12、槽长为69 mm、膜厚为3.05 μm为例。图7(a)为不同螺旋角下的密封压力云图。随着螺旋角的增大,密封的槽根压力增加,螺旋角为14°时槽根压力最小(11 536 379 Pa),螺旋角为17°时槽根压力最大(12 815 620 Pa)。在一定范围内,通过增大螺旋角可以增加气膜最大压力。这是由于密封槽和密封坝区存在楔形台阶,这对流体起到导向作用,气体沿槽内间隙减小的方向流动,气体进一步被压缩,使得动压效果增强,端面气膜开启力增大。

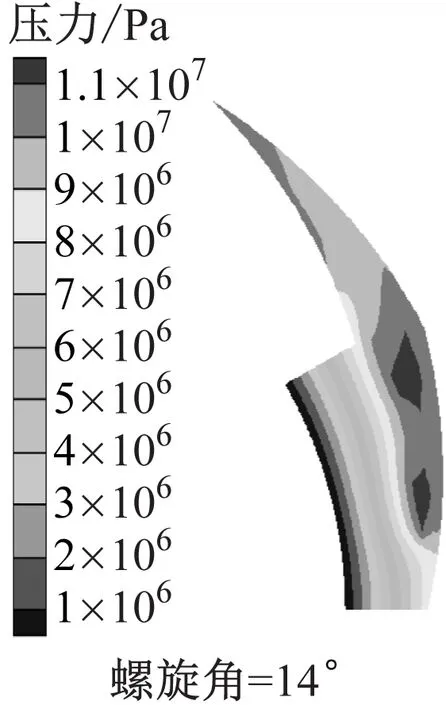
(a) 密封压力云图

图7(b)为不同螺旋角下气膜开启力、泄漏量和刚漏比的折线柱状图。随着螺旋角的增大,端面气膜开启力和泄漏量也增大,刚漏比减小。螺旋角由14°增加至17°时,气膜开启力增大3.1%,泄漏量增加4.3%,密封刚漏比降低7.2%。螺旋角增加使得槽区径向尺度增加,从而吸入气体量增加,气膜开启力增大。单位时间内流入螺旋槽的CO2气体增加,在一定空间内气体的径向流动速度增大,也使得向外流出的气体量增加,导致泄漏量增加,密封综合性能下降。

以槽深为5 μm、螺旋角为15°、槽长为69 mm、膜厚为3.05 μm为例。图8(a)为不同槽数下的密封压力云图。槽根气膜最大压力与槽数之间的关系并非单调的,开槽数为12时槽根气膜最大压力最高,为12 023 131 Pa;开槽数为18时槽根气膜最大压力最低,为11 200 669 Pa。相对于开槽数为12,虽然开槽数增加后槽根最大膜压略有降低,但槽区总面积也相应增大,径向气膜压力分布更加均匀,密封的支撑性能整体保持稳定。

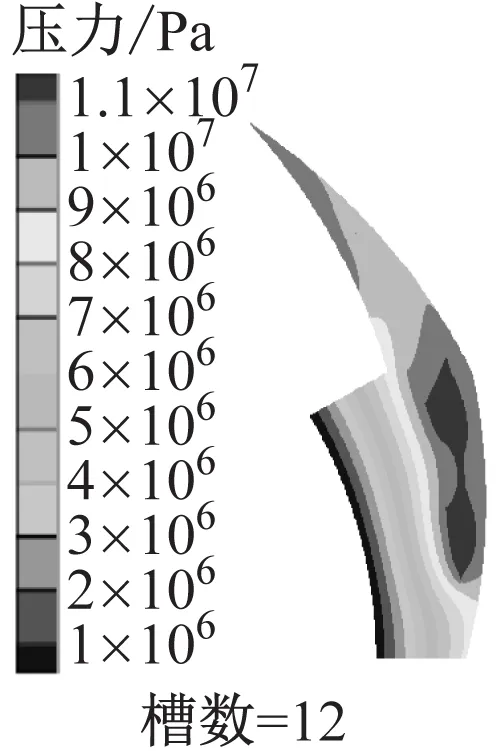
(a) 密封压力云图

图8(b)为不同开槽数下气膜开启力、泄漏量和刚漏比的折线柱状图。端面气膜开启力随槽数的增加有所波动,开槽数为16时气膜开启力最大,开槽数为20时气膜开启力最小。槽数的变化对气膜开启力的影响并不明显。泄漏量随着开槽数的增加而降低,开槽数为12时泄漏量最高,开槽数为24时泄漏量最低,与开槽数为12时相比泄漏量下降50%,槽数增加使得每个槽区的面积减小,单个槽区流体泄漏通道变小,使得泄漏量在一定槽数内降低,因此增加一定的开槽数可以使泄漏量显著降低。刚漏比随槽数的增加而逐渐增大,开槽数为12时刚漏比最小,开槽数为24时刚漏比最大,相比开槽数为12时刚漏比增大近1倍,密封综合性能显著提升。

以槽深为5 μm、螺旋角为15°、槽长为69 mm、槽数为12为例。图9(a)为不同膜厚下的密封压力云图。槽根气膜最大压力随膜厚的增加而降低,气膜厚度为2.05 μm时槽根气膜最大压力最高,为18 344 786 Pa;气膜厚度为7.05 μm时槽根气膜最大压力最低,为9 985 602.4 Pa。膜厚较小时泵送效应较高,凹槽末端形成局部高压。泵送效应是由凹槽中的黏性泵送以及限制流体向外流动的坝区中离心效应和黏性摩擦效应引起的。膜厚增加导致泵送效应降低,动压效应不足,密封坝区域的周向压力分布更均匀,会对槽根最大压力产生不利影响,从而使得端面气膜开启力显著降低。

(a) 密封压力云图

图9(b)为不同气膜厚度下气膜开启力、泄漏量和刚漏比的折线柱状图。端面气膜开启力随着膜厚的增加而降低。膜厚较小时,SCO2的黏性剪切作用更强,吸入的气体量增多,使得凹槽压力较高,密封坝区域的离心效应更强,导致端面气膜开启力增大。泄漏量随着气膜厚度的增加而增加,气膜厚度的增加使得动环与静环之间的间隙增大,流体流通通道扩大,导致干气密封泄漏量增加。随着膜厚的增加,干气密封刚漏比明显下降,气膜厚度为2.05 μm时刚漏比最大,气膜厚度为7.05 μm时刚漏比最小,气膜厚度的增加使密封综合性能急剧下降。

综上,槽长为69 mm、槽深为5 μm、槽数为12、螺旋角为15°、气膜厚度为2.05 μm时干气密封的刚漏比最大,密封综合性能最好。

4 结 论

(1) 相较于螺旋槽干气密封,组合型螺旋槽干气密封密封端面气膜开启力提高1.1%,泄漏量降低18.8%,密封性能更佳。

(2) 组合型螺旋槽干气密封的几何参数对密封性能具有较大的影响。槽长较大的密封在密封坝区具有更高的黏性摩擦和离心效应,槽长由66 mm增加至69 mm时,泄漏量降低12.73%,刚漏比增加13.34%,密封性能提高;槽深由3 μm增加至10 μm时,密封坝区的离心效应降低,泄漏量增加43.24%,刚漏比下降10.93%,密封性能降低;螺旋角由14°增加至17°时,泄漏量增加4.3%,刚漏比下降7.2%,密封性能降低;槽数由12增加至24时,泄漏量下降50%,刚漏比增大近1倍,密封综合性能显著提高;随着气膜厚度的增加,泄漏量明显增加,刚漏比急剧下降,密封综合性能显著降低。